“情境·设问·探究”模式下的章末总结课教学实践——以北师大版高中数学教材“计数原理”章末总结课教学为例

章建荣 (江西省南昌市铁路第一中学 330002)

在高中数学章末总结课的教学中,创设合理的问题情境是十分重要的。合理的问题情境能够引导学生进行自主思考、自主探究,帮助学生很好地应用所学的知识解决实际问题,本文以北师大版高中数学教材的“计数原理”章末总结课的教学为例来谈一谈章末总结课的教学探索。

一、教学目标

1.结合实例,理解排列与组合的概念和区别,感悟计数原理的基本思想,运用计数原理探索排列、组合问题;

2.通过流程图或表格的形式,直观地呈现“一件事”的完成过程,揭示分类加法计数原理和分步乘法计数原理的本质,并运用计数原理解决实际问题;

3.在运用计数原理求解问题的过程中,体会排列与组合的目的和意义,发展数学运算、逻辑推理等核心素养。

二、教学重点与难点

重点:1.将 “一件事”的完成过程用流程图或表格的方式呈现;

2.利用分类加法计数原理和分步乘法计数原理求解问题。

难点:1.认识两个基本计数原理与排列、组合的内在联系;

2.利用计数原理推导二项式定理。

三、教学过程

摸球问题是古典概型中一类重要的问题。由于摸球的方式、球颜色的搭配及最终考虑的问题不同,其内容可以说是形形色色、千差万别。

1.活动探究

如图1,袋子中有红色、黄色、黑色等多种颜色的球若干个,这些球除颜色外完全相同,现有编号为1,2,3,4,…的盒子,这些盒子除编号外完全相同。

图1

【探究一】若袋子中有红球、黄球、黑球、蓝球各1个。

(1)从这4个球中抽取3个,共有多少种取法?

(2)从这4 个球中抽取3 个,分别放入1 到3号的盒子中,每个盒子放1 个球,共有多少种放法?

师生活动:

问题1:从这4 个球中抽取3 个,有多少种取法?

问题2:你是否还有其他方法解决此问题?

“从这4个球中去掉1个”的方法数和“从4个球中抽取3个”的方法数相等,即种。

问题3:第(2)问与第(1)问有什么关系?

“从这4个球中抽取3个,分别放入1到3号的盒子中,每个盒子放1个球”这件事可以分为两步,第一步就是从这4个球中抽取3个,第二步是将这3个球进行排列。

如图2,我们采用流程图的方式呈现“从这4个球中抽取3个,分别放入1到3号的盒子中,每个盒子放1个球”这件事的完成过程。

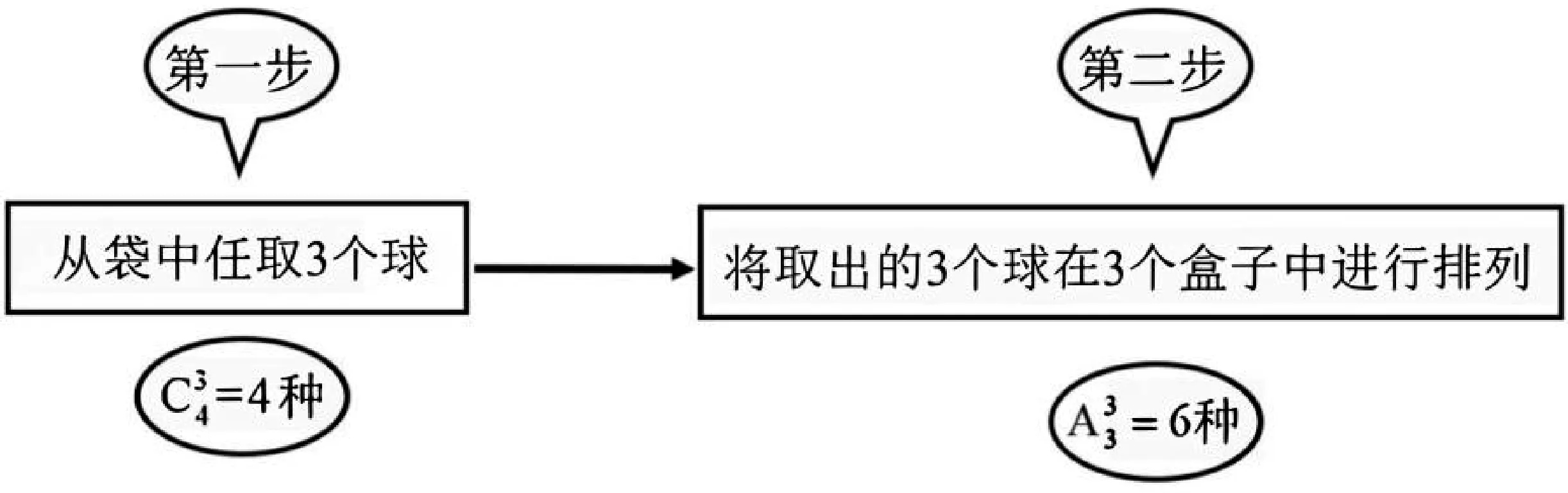
图2

问题4:我们还可以采用其他分步的方式完成“从这4个球中抽取3个,分别放入1到3号的盒子中,每个盒子放1个球”吗? 该如何操作?

①如图3,我们可以采用流程图的方式呈现“从这4个球中抽取3个,分别放入1到3号的盒子中,每个盒子放1个球”这件事的完成过程。

图3

共有4×3×2=24种方法。

②我们也可以采用表格的方式呈现“从这4个球中抽取3个,分别放入1到3号的盒子中,每个盒子放一个球”这件事的完成过程,如表1。

表1

共有4×3×2=24种方法。

问题5:从“4×3×2=24”中,有什么发现吗?

归纳:从n个不同的球中取出m个球进行排列,共有种方法。

从n个不同的球中取出m个球进行组合,共有种方法。

其实排列与组合就是我们在使用计数原理求解问题的过程中发现的规律,为了简化解题过程,我们建立计数模型,当我们以后遇到这类问题时,可以直接使用排列数公式或组合数公式简化我们的解题过程。

排列与组合的联系与区别:

①共同点:两者都是关于从n个不同元素中取出m(m≤n,且m,n∈N+)个元素的计数问题。

②不同点:排列需要考虑元素顺序,组合不需要考虑元素顺序。

③排列中有组合的思想,组合也可以由排列来处理。

【设计意图】

(1)通过具体的实际问题,学生体会使用流程图或表格的方式直观呈现“一件事”的完成过程,突出解决计数问题的核心。

(2)第①问是组合问题,第①问的另一种解法体现的是一种反向思维,它是从问题对立面的角度思考问题,同时解释了这个模型。

(3)第②问设置在第①问的后面,主要是引导学生在处理第②问时,可以以第①问为基础,体现了排列问题可以看成先组合再全排列,这也为解决组合问题提供了一种逆向思维,同时揭示了排列与组合是我们为了便于解决计数问题而建立的两个数学模型,其本质还是两种基本计数原理。

【探究二】若袋子中有红球、黄球、黑球、蓝球、白球、绿球各1个。

(1)将这6个球分配到编号为1,2,3的3个盒子中,每个盒子中至少有1个球。

①若3个盒子中球的个数各不相同,则有多少种不同的分配方案?

②若1个盒子中有4个球,则有多少种不同的分配方案?

(2)若将这6个球分配到编号为1,2的2个盒子中,且每个盒子中球的个数大于其编号,则有多少种不同的分配方案?

师生活动:

问题1:袋子中一共有6个球,分到3个盒子中,每个盒子中至少有1个球,且每个盒子中球的个数各不相同,那么盒子中球的个数分别是多少个呢?

分别是1,2,3个。

问题2:在处理计数问题时,可以尝试先组合再排列的思路处理问题,所以我们如何解答第①问呢?

首先将这6个球分成三组,且每组球的个数分别为1,2,3个,有种;再将这三个组合排列到3个盒子中,有种,由分步乘法计数原理可知:共有360种不同的分配方案。

问题3:袋子中一共有6个球,如果有1个盒子中有4个球,3个盒子中球的个数分别是多少个呢? 若先分组,再排列,则共有多少种分配方案呢?

每个盒子中球的个数分别是1,1,4个。

首先将这6个球分成三组,且每组球的个数分别为1,1,4个,有种;再将这三个组合排列到3个盒子中,有种。由分步乘法计数原理可知:共有种不同的分配方案。

问题4:袋子中一共有6个球,如果将这6个球分配到编号为1,2的2个盒子中,且每个盒子中球的个数大于其编号,那么1号盒子中球的个数至少多少个? 盒子中球的个数一共有多少种情况呢?

1号盒子中球的个数至少为2个。

用表格呈现所有可能的情况,如表2。

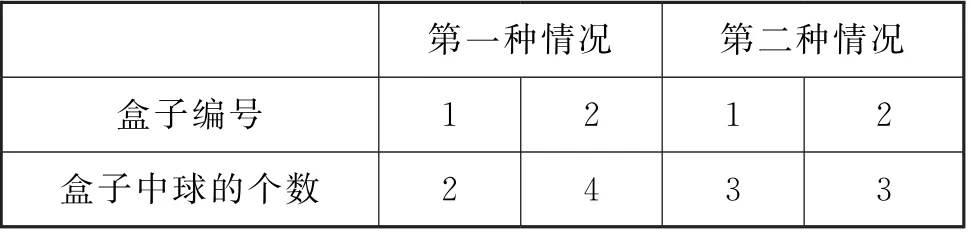
表2

我们按照上面的定额分组分配问题的求解办法求解每一种情况即可,所以共有种不同的分配方案。

【设计意图】

(1)第①问和第②问都是定额的分组分配问题,结合实际情境帮助学生回顾分组分配问题的处理思路——先分组再排列。

(2)第②问相比第①问的区别是有平均分组,在分组分配问题中,面对平均分组的问题,引导学生回顾该怎么处理,帮助学生巩固解题方法。

(3)第②问是不定额的分组分配问题,通过这个问题帮助学生巩固不定额的分组分配问题的处理思路——先分类再定额分组分配。

【探究三】现有编号为1,2,…,7 的7 个盒子,按编号排序,将红色、黄色、蓝色、黑色4个除颜色外完全相同的球全部放入7个盒子中,每个盒子最多放1个球,则恰好有2个相邻的空盒且红球与黄球不相邻的放法共有______种。

师生活动:

问题1:有相邻和不相邻的问题,先考虑相邻还是不相邻呢?

可以先考虑相邻。

问题2:我们要分步完成,可以分成几步完成呢?

可以分三步完成。

第一步,先将4个球放到4个盒子中,在不考虑红球和黄球不相邻的情况下,共有种放法。

第二步,再考虑空盒相邻的情况,只需要将两个空盒捆绑,和剩余一个空盒插空即可,共有种放法。

第三步,最后考虑红球和黄球不相邻的问题。

问题3:红球和黄球不相邻的问题,我们能否转化成相邻的问题呢?

【设计意图】

(1)结合实际情境帮助学生回顾相邻和不相邻问题的处理思路——插空法。

(2)面对不相邻的问题,引导学生将不相邻的问题转化为相邻的问题进行求解,渗透转化与化归思想。

【探究四】现有编号为1,2,3,4,5,6 的6个盒子,按编号排序,每个盒子中分别放有1个红球和1个黄球,从每个盒子中任取1个球。

(1)若选出4 个红球2 个黄球,则有多少种取法?

(2)从6个盒子中各取1个球,一共有多少种取法?

师生活动:

问题1:选出4个红球2个黄球,即从4个盒子中选出了红球,2个盒子中选出了黄球,共有多少种取法呢?

从6个盒子中任选4个盒子取出红球,在剩下的2个盒子中取出黄球,所以共有种取法。

问题2:从6个盒子中各取1个球,要取多少次? 共有多少种取法?

取6 次,则可以分成6 步来完成这件事,如表3。

表3

共有26种取法。

问题3:在第①问的基础上,换一种角度思考,抽取出来球的个数一共是6个,取出来的球有哪些情况呢?

共有7种情况,如表4。

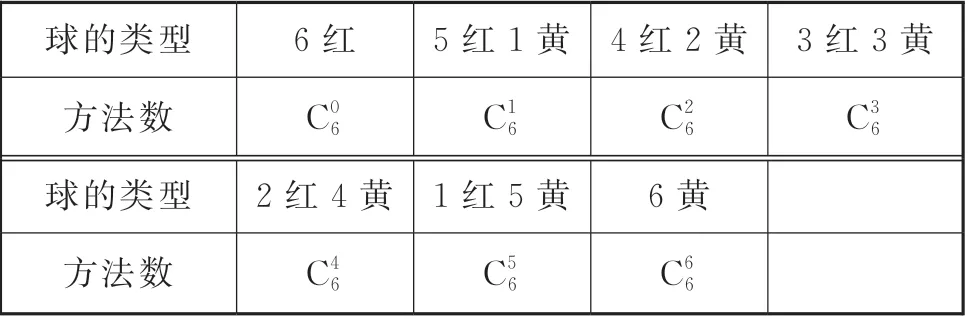
表4

【设计意图】

(1)第①问通过摸球模型解释二项式展开式中a4b2的系数,利用计数原理分析问题,有效地帮助学生理解抽象的知识,从具体到抽象,增强了对二项式定理的直观理解,起到巩固知识的作用。

(2)第②问是在第①问的基础上,通过摸球模型解释二项式系数的性质,感悟排列、组合与二项式定理之间的关系,培养学生观察归纳、抽象概括的能力。

2.总结提升

章节内容,如图4。

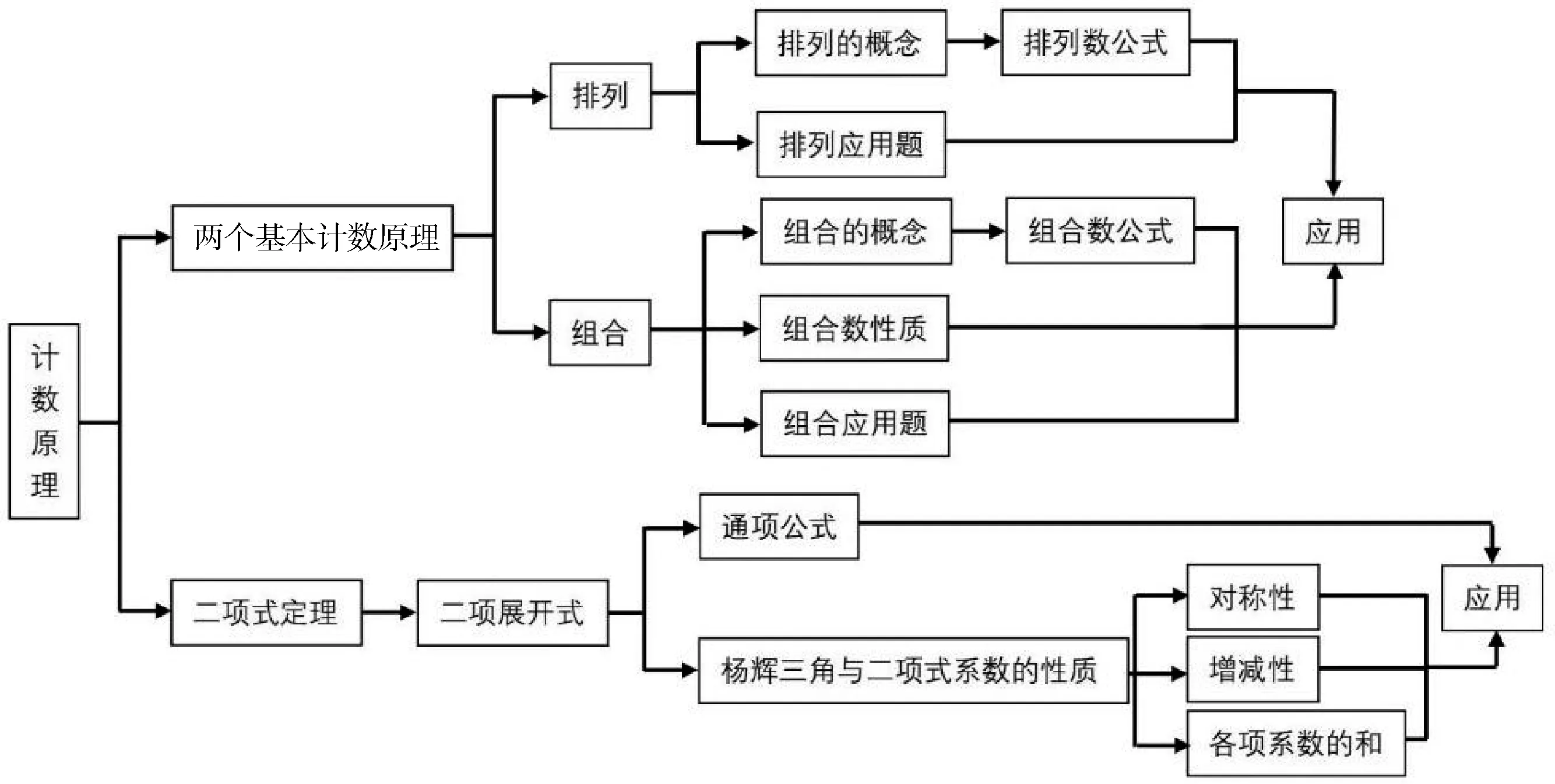
图4

核心知识:两个基本计数原理

数学方法:图示表格(实际问题直观化)、化整为零(复杂问题简单化)

数学思想:数形结合、转化与化归、分类讨论

【设计意图】

通过四个探究,引导学生经历使用计数原理解决问题,从中提炼出排列与组合问题的核心其实还是计数原理。在具体到抽象的过程中,进一步发展学生类比、归纳等推理能力,体会数形结合、分类讨论、转化与化归等思想。不但使学生“知其然”,而且让学生“知其所以然”,体现以学生为本,让学生在质疑、探究、理解、归纳和运用的过程中深刻理解排列、组合之间的关系,感悟排列与组合的联系与区别,以及排列、组合与二项式定理之间的关系,发展数学运算、逻辑推理和数学建模等核心素养。

3.课后作业

(1)2名医生和4名护士将被分配到2所学校为学生体检,每所学校分配1名医生和2名护士,共有多少种分配方法?

(2)6名同学排成一排,其中甲、乙两人不相邻的排法共有多少种?

(3)正六边形有1个中心和6个顶点,若以这7个点中的3个点为顶点组成三角形,则共能组成多少个三角形?

四、教学反思

实践证明,在“计数原理”章末总结课的教学中,采取“问题探究”的模式,能够有效地彰显学生在章末总结课中的主体地位,通过一类问题的探究,揭示知识的本质,突出知识之间的关系,通过问题引领学生在课堂上开展自主化数学探究活动,建构知识体系,促进数学思维能力的提升,从而高效地达到章末总结课的教学目标。