非均匀温度分布下温差发电系统的多峰值寻优

王 涛，胡申华，马湘蓉，程 昊

(1.南京工程学院电力工程学院，江苏南京 211167；2.南京工程学院能源与动力工程学院，江苏南京 211167；3.南京工程学院信息与通信工程学院，江苏南京 211167)

随着全球经济发展，不可再生能源被大规模开采，可持续发展和环境保护不得不提上日程。面对有限的资源[1]和人们日益增长的能源需求，如何解决这一矛盾，成为了全球的重要问题。所以物尽其能，提高资源的利用率成为了当下研究的方向。温差发电是一种可以将生产过程中多余的热量加以利用转化为电能的技术，使用温差发电既可以提升资源的利用率，也起到了保护环境的作用[2-3]。

由于光伏系统的输出功率容易受到环境等外部因素的影响，具有非线性的特点，最大功率追踪(MPPT)算法最早对光伏电池的最大功率进行实时追踪，确保功率最大化输出。温差发电系统也存在输出功率容易受到环境等外部因素的影响，文献[4]通过4 片温差发电片进行串联实验，绘制出了实际的温差发电片的PV 曲线，实验数据表明温差发电片的PV 曲线呈现非线性的特点。MPPT 也被广泛用于温差发电系统，随着智能算法的兴起，越来越多的智能算法被应用到MPPT 中，推动了MPPT 技术的迅速发展。传统的MPPT 控制算法有扰动观察法[5-7]、电导增量法[8]、恒定电压法，但是传统的MPPT 控制算法还存在明显的缺陷，不能满足高精度、复杂的应用场景。在传统MPPT 算法的基础上，变步长的扰动观察法[9]和变步长的电导增量法[10]、线性外推法[11]等大量的改进算法被提出。在使用集中式MPPT 控制模型时，工作场景的外部因素影响会导致多个功率极值点的出现，此时传统的MPPT 控制算法无法区分局部最优和全局最优。智能优化算法则可以很好地解决局部最优和全局最优的问题，例如重力搜索算法(GSA)[12-13]，粒子群算法(PSO)[14]、均衡优化算法(EO)[15-16]、罗盘搜索算法[17]都已经成功地应用到了半导体温差发电片(TEG)多峰值系统的最大功率追踪，但是这些智能优化算法通常存在搜索时间长和需要经过大量迭代等缺陷，会造成最大功率追踪的效率较慢。

自适应罗盘算法(ACS)具有强大的快速搜素能力，万有引力搜素算法(GSA)具有较优的全局搜素能力，本文将二者的优点结合，提出了一种新型的混合优化算法(GSA-ACS)，用于实现热电片发电系统的最大功率追踪。本文分别从恒定温度的场景、温度非均匀分布的场景、变化温度的场景，与扰动观察法(P&O)、均衡优化算法(EO)、ACS、GSA相比较，GSA-ACS 能以更快的速度和更高的质量达到全局的最大功率点。

1 热电模块及系统建模

1.1 TEG 模型

TEG 系统可以等效为电压源和电阻串联，其内部的开路电压和内阻均会随着温度的变化而变化，图1 所示为TEG 的内部结构。当冷端和热端出现温差的时候，开路电压和温差关系可以描述为：

图1 TEG内部结构

TEG 可以等效为如图2 所示，一个电压源和电阻串联。RTEG代表温差发电片的内阻，RL代表负载电阻，电路中负载电阻想要获得最大功率。根据最大功率传输定理，当RTEG=RL时，RL获得最大功率，最大功率Pmax可以表示为：

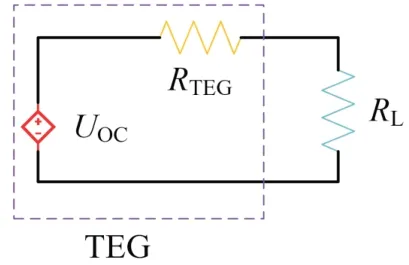
图2 TEG等效图

1.2 TEG 系统的特性曲线

实际的使用场合复杂多变，不同设备对功率的需求也不一样，但是一片TEG 模块输出的电压是很有限的，图3 为单个TEG 不同温差下输出的PU 曲线。有时需要将多个TEG 模块串联、并联进行组合排列以满足要求，图4 为多个TEG 串并联MPPT 输出的PU 曲线。典型的TEG 系统的结构有：集中式TEG、组串式TEG 系统、模块式TEG 系统。本文使用的是集中式TEG 系统，多个TEG 模块串联、并联进行组合，通过一个MPPT 控制整个系统，操作相对简单，维护成本相对较低。

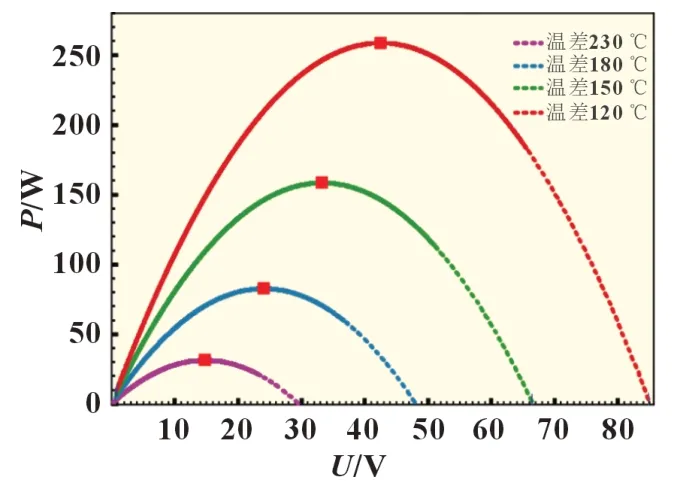
图3 单个TEG不同温差下输出的PU曲线

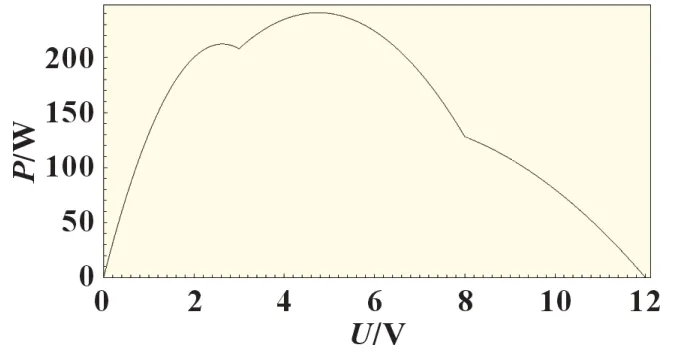
图4 多个TEG串并联MPPT输出的PU曲线

2 三种算法

2.1 重力搜索算法

在D维空间中有N个粒子，粒子i的位置可以表示为：

依据万有引力，t时刻粒子j对粒子的作用力可以表示为：

式中：Rij(t)为粒子i和粒子j之间的欧氏距离；ε 为一个很小的常量；Mik(t)、Mjk(t)分别为粒子i和粒子j的惯性质量；G(t)为万有引力常数，其大小会随着t的增加而递减，可以表示为式(5)。

1935年，祖父在汉口去世，享年86岁。在这之前，祖父在庐山脚下的威家买了一大片山林做坟地，又买下一些邻近的田地，供看坟人免费租种。祖父出殡时，开道幡为时任上海市市长吴铁成亲书，至交皆乘马车，逶迤数里，棺椁自武汉运至威家落土下葬，沿途路祭不断。

粒子i所受到的合力为：

其中randj是[0,1]之间的随机数，D维空间中粒子i在t时刻的加速度可以表示为：

D维空间中粒子i的质量Mik的计算公式如下：

在每次迭代过程中，粒子的速度和位置都需要进行更新，更新公式如下：

2.2 罗盘搜索算法

罗盘搜索算法是基于传统的模式搜索提出的，分为三个过程：(1)模式矩阵的确定；(2)移动探索；(3)模式移动。

(1)模式矩阵[18]

当变量数目为n时，有2n种搜索模式，当n=2，模式矩阵可以表示为：

Δi为变量i的优化步长。

(2)移动探索、模式移动

步骤1：基于当前的解先进行正向移动，将正向移动获取的适应度与当前适应度相比较。如正向的适应度比当前的值更优，则记录正向移动的值为当前值。否则进入步骤2。

步骤2：否则进行反向移动，将反向移动获取的适应度与当前适应度相比较，如反向的适应度比当前的值更优，则记录正向移动的值为当前值。否则进入步骤3。

步骤3：如果当前的值比正向、反向的适应度都更优，缩短步长Δi，重新进行步骤1。

(3)为了进一步提升全局搜索的能力，利用已有的最优解对每个变量的搜索方向进行优化，引入正向搜索的概率和反向搜索的概率。

2.3 GSA-ACS 混合优化算法

将重力搜索算法用于非均匀温度分布下的MPPT 控制，利用不同粒子间的引力不断调整粒子的位置，实现MPPT 追踪。引入了ACS 算法让粒子快速接近最优解，优化后的粒子质量更新公式如下：

式中：E反映了GSA 和ACS 之间的交互方式；nmin、nmid、nmax分别为最小迭代次数、中等迭代次数、最大迭代次数，这些参数需要依据具体的实验对象进行设置。

GSA 作为全局搜索算法具有随机性质，将这些全局中的最优节点交给ACS 进行快速搜索，有利于快速寻找更优值，并给GSA 的下一次迭代，这种方式有助于在更短的时间内找到最优值。GSA-ACS 混合优化算法流程如图5 所示。

图5 GSA-ACS混合优化算法流程

3 基于混合优化算法的集中式TEG 系统MPPT 设计

3.1 占空比和适应度函数

集中式温差发电系统是通过调整占空比控制MOS 管的开断，以达到阻抗匹配，实现最大功率的追踪。占空比Dn的大小是需要设置上下限的，上下限为0，1。

适应度函数Fitn(Dn)是表示系统输出功率的函数，Uin(Dn)和Iin(Dn)都随着Dn的变化而变化。适应函数的计算公式如下：

式中：Uin(Dn)和Iin(Dn)分别为Dn输入MPPT 系统输出的电压和电流。

3.2 仿真模型

利用Simulink 搭建的仿真模型对GSA-ACS 算法进行仿真验证，并和GSA、ACS、P&Q 算法进行对比。模拟非均匀温度分布、温度阶跃变化这两种情况。图6 给出了MPPT 设计的总体框架，TEG 的连接方式使用的是集中式，TEG 的连接方式是先串联后并联，每20 个TEG 进行串联组成一个小的单元，3 个这样的TEG 单元进行并联，TEG 的具体参数如表1所示。仿真环境是基于MATLAB/Simulink 2021a 搭建，机器的配置是Intel Core 5 CPU 和8 GB RAM，搭建的仿真模型如图7 所示。

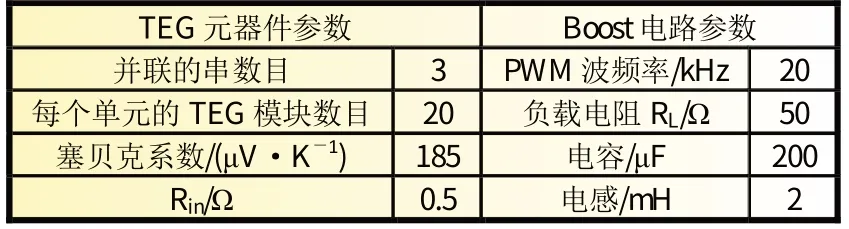
表1 TEG系统的主要参数

图6 总体设计图

图7 MPPT控制系统的仿真模型

4 仿真与分析

4.1 非均匀分布温度恒定

TEG 处于非均匀温度分布下，冷热源温度保持不变，第一个单元的冷端温度为20 ℃，热端温度250 ℃。第二个单元是冷端温度为20 ℃，热端温度150 ℃。第三个单元的冷端温度为20 ℃，热端温度50 ℃。如图8 所示，分别对功率、占空比、电压进行分析。扰动观察法会陷入局部最大值点，导致无法追踪到最大功率点，算法失效。ACS、GSA、GSA-ACS 都具有一定的全局搜索功能，占空比输出的波形均为先大范围的震荡后收敛最终稳定在某一工作点。P&Q、ACS、GSA、GSA-ACS 最终稳定输出的最大功率分别为155.2、222.5、222.8、222.8 W。GSA-ACS 兼顾了能稳定在全局最优和能快速迭代达到收敛。

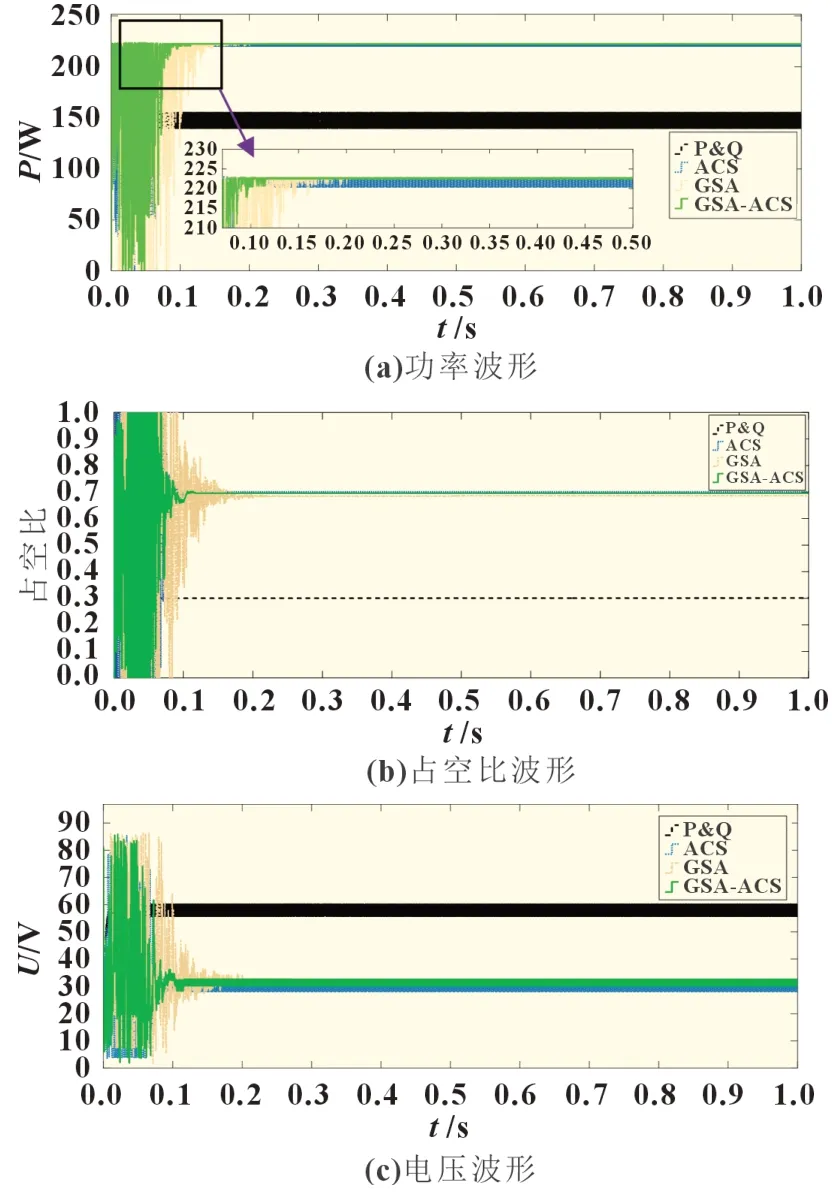
图8 温度恒定下的算法对比

4.2 非均匀温度下的温度阶跃变化

非均匀温度下的温度阶跃变化，三个单元的冷端温度均为20 ℃，阶跃前的热端温度分别为200、100、30 ℃，阶跃后的热端温度分别为250、150、50 ℃。热端温度的变化曲线如图9 所示。为了进一步验证算法在特殊环境下的可靠性，模拟温度阶跃变化的环境。从图10 可得，在温度阶跃变化的环境下，除P&Q 之外的算法都可以稳定在最大功率。GSA-ACS相较于GSA、ACS 算法都展现出了收敛速度快、震荡幅度小的特点。

图9 温度阶跃变化图

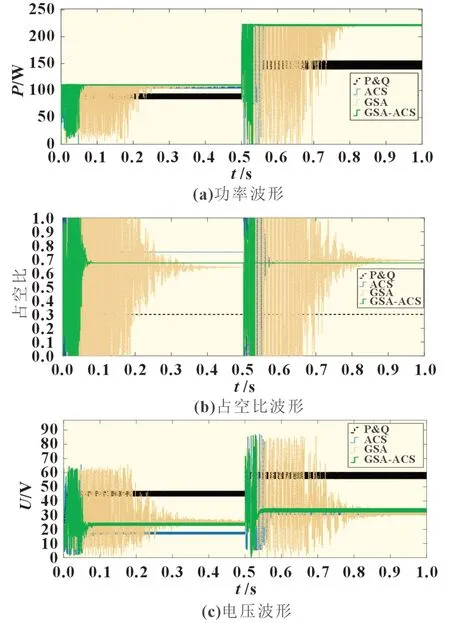
图10 温度阶跃变化下的算法对比

表2 给出了P&Q、ACS、GSA、GSA-ACS 四种算法分别在温度恒定、温度阶跃下的数据，可以看出P&Q 最大输出功率都是最小的。GSA 的迭代周期很长，在温度恒定的场合收敛时间为0.2 s，在温度阶跃的场景下收敛的时间分别为0.4、0.32 s，都远大于ACS、GSA-ACS。ACS 输出的功率在温度恒定的场合为222.4 W，在温度阶跃的场景下输出的功率分别为111 和222 W，均小于GSA、GSA-ACS。

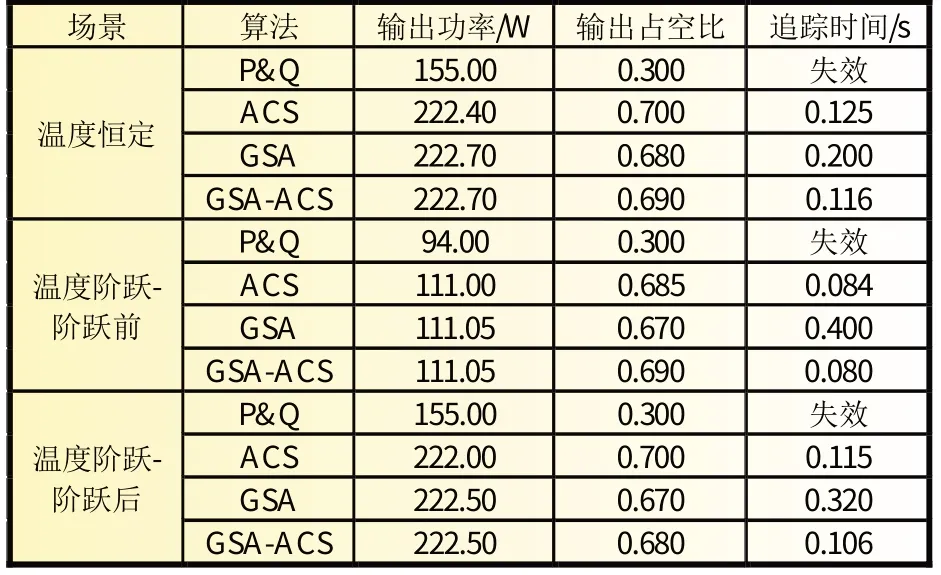
表2 P&Q、ACS、GSA、GSA-ACS算法的数据分析

5 结论

TEG 阵列进行串并联组合，在非均匀温度分布的场景下，传统的扰动观法陷入局部最大值，导致算法无法追踪到全局最大功率点，造成该算法失效。仿真结果表明在恒温环境下，GSA-ACS 混合优化算法的追踪所用时间比GSA、ACS算法分别快了0.084、0.009 s,GSA-ACS 混合优化算法的最大输出功率与GSA 一致，比ACS 算法的输出功率高出0.3 W。在温度发生阶跃变化的环境下，GSA-ACS 混合优化算法依旧保持着明显的优势，温度发生阶跃前的追踪时间为0.08 s，比GSA、ACS 算法分别快了0.32、0.004 s。温度阶跃后GSAACS 混合优化算法只使用了0.106 s 完成追踪，比GSA、ACS算法分别快了0.214、0.009 s。从上述分析可得，GSA-ACS 混合优化算法无论是在温度恒定的场合还是在温度发生阶跃变化的场合，其追踪的时间和最大输出功率都具有一定的优势。