基于改进Bayes信息量准则的锂电池自适应变阶AVO模型

寇发荣，门 浩，王甜甜，王思俊，罗 希

(西安科技大学机械工程学院，陕西西安 710054)

锂电池作为纯电动汽车的直接动力源，其状态的估计直接影响整车性能[1]。准确、可靠的模型对锂电池的研究具有重要意义，建立电池模型是进行荷电状态(SOC)估计、功率状态(SOP)估计、健康状态(SOH)估计等工作的基础[2]。

目前，学者们主要通过探究锂电池的行为特性与反应机理对其进行建模。常用的电池模型有电化学模型、神经网络模型、分数阶模型和等效电路模型[3]。等效电路模型通过将电阻、电容等电器元件进行组合排列，模拟电池的静态及动态特性。模型具有结构简单、运算负荷较小的特点[4]。等效电路模型的精度取决于RC 环节的阶数，当模型阶数增加时，精度随之提升；但随阶数的增加，模型复杂度会大幅增加[5]。三阶及三阶以上RC 等效模型会出现过度拟合现象，导致其实用性降低[6]。已有研究表明：一阶RC 模型往往不能满足高精度场合的需求；二阶RC 模型考虑了欧姆、浓差及电化学极化特性的影响，能更精确地描述锂离子电池的动静态特性[7]，其结构相对较复杂，计算量增大。为保证模型精度同时提高其实用价值，对模型阶数进行实时动态调整；综合考虑模型的复杂度与计算量、精度与实用性之间的矛盾，选用一阶、二阶RC 自适应变阶(adaptive variable-order，AVO)模型，该模型可在电压变化剧烈的区域进行升阶处理，保证模型精度；在电压变化缓慢的区域降阶处理，达到除冗和降低计算量的目的。

本文提出一种融合贝叶斯信息量准则(Bayes information criterion，BIC)和樽海鞘优化算法(salp swarm algorithm,SSA)的AVO 模型，通过端电压误差Bayes 信息量确定模型阶数的最优解，以最优拟合度、最小平均误差和为目标函数，利用樽海鞘优化算法搜索模型阶数的全局最优解，使模型变阶效果达到最佳。最终通过仿真和实验，验证AVO 模型的精确性与实用性。

1 锂电池自适应变阶模型

1.1 自适应变阶等效电路模型

锂电池等效电路模型(equivalent circuit model，ECM)在工程应用中主要有一阶RC 模型、二阶RC 模型等。模型精度往往与阶数成正比，理想情况下，当低阶模型拟合度较高时，模型可由二阶降为一阶，达到降阶除冗的效果。当低阶模型拟合精度不足时，模型亦可由一阶切换为二阶，提升模型精度。

AVO 模型以Bayes 信息量准则作为变阶标准，通过端电压误差得出各时刻对应的BIC 值，对模型实现动态变阶。AVO 模型等效电路如图1 所示。

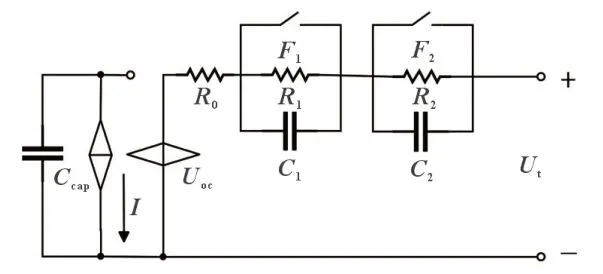
图1 AVO模型等效电路

图1 中：Ccap为电池容量；I为电流；Uoc为开路电压；R0为欧姆内阻；R1、R2、C1、C2分别为模型的电阻、电容参数；Ut为端电压；F1、F2为模型的切换开关。

根据基尔霍夫定律，AVO 等效电路模型的数学方程可表示为：

式中：l为RC 环节个数，其值为1、2。

RC 环节的状态方程可表示为：

式中：Un为RC 环节极化电压。

通过控制开关F1和F2的状态，实现AVO 模型阶数切换。AVO 模型阶数与开关状态的对应关系如表1 所示。其中，状态T 表示电路接通，O 表示电路断开。

表1 模型阶数与开关状态对应关系

1.2 模型阶数的确定

模型阶数确立的关键是变阶指标的选取。赤池信息量准则(Akaike information criterion，AIC)与贝叶斯信息量准则(BIC)被广泛应用到模型的选择中，用来评判模型拟合的优良性[8]。

AIC 以信息熵来衡量模型拟合优良性的一种指标，通常可表述为[9]：

式中：K为模型参数数目；NT为实验采样总数；L为模型极大似然函数；2K/NT为模型惩罚项，模型参数数目K值决定模型精简程度；lnL为模型拟合度，其值越小代表此时模型越精确。

BIC 在AIC 的基础上引入模型样本容量nm，极大地弥补了AIC 惩罚项与样本容量无关的缺陷。引入模型端电压误差平方和对BIC 拟合项进行改进，假设模型的误差服从正态分布，改进的BIC 函数为：

式中：d为电池端电压与模型端电压的误差。

为得到最优的BIC 评定标准，在改进的BIC 惩罚项中引入惩罚系数s，对拟合程度的不敏感度进行调节。使用BIC 准则评定时，认为一阶RC 模型包含参数Ccap、R0、R1、C1，共计4个；二阶RC 模型在一阶的基础上增加了参数R2和C2，共计6个。因此，认为在RC 等效电路模型中，p阶模型参数数目K的取值为2p+2。

最优BIC 函数为：

计算同时刻不同阶数的BIC 值，较小的BIC 值所对应的模型阶数即为该时刻拟合效果最佳的阶数。BICopt(t,p)为t时刻p阶模型对应的最优BIC 值。当前t时刻AVO 模型的最优BIC 值为：

1.3 模型阶数的最优解

在模型阶数标定过程中，参数的选取会直接影响BIC 的取值，进一步影响阶数的确定。针对BIC 参数选取的问题，本文利用樽海鞘优化算法及设定的优化条件对BIC 参数进行寻优。

樽海鞘优化算法是模拟樽海鞘群在海洋中聚集与狩猎行为而创立的一种算法[10]，其数学模型简单、算法寻优精度高。最优拟合度、最小平均误差和目标函数分别为：

式中：NHPPC为HPPC 工况实验下的总采样数；Ut,j(nm,s)为模型样本容量为nm、惩罚系数为s时，AVO 模型第i个端电压输出值；Ut,j为端电压第i个采样值。

在n维搜索空间中定义樽海鞘位置：其中N为给定问题的变量个数，包含样本容量nm和惩罚系数s；假设F为给定搜索空间下的狩猎目标，所有樽海鞘的位置都存储于矩阵X中；Bmaxj、Bminj分别代表第j维上的取值上、下边界；狩猎过程中迭代时差取值为1。

将樽海鞘群划分为领头者和追随者，寻优过程中领头者处于种群最前端，追随者紧随其后。在n维空间寻优时，樽海鞘的数学模型中，领头者在j 维空间中的位置为：

式中：Xj为j维空间下待狩猎目标位置；c2、c3为[0,1]之间随机数，c2决定领头者移动长度，c3决定移动的正反向。

收敛因子c1的设定影响算法的平衡探索和局部开发能力，其表达式为：

式中：tmax为最大迭代次数。

第i个追随者在第j维空间中的位置为：

取初始速度ν0=0，则式(10)可表达为：

基于空间限制，对算法中的主要参数做出如下限定：变量个数N设定为2；样本容量nm的取值设定为整个放电过程中采样点总数的1%～5%；惩罚系数s设定为1～5。SSA 寻优流程如图2 所示。

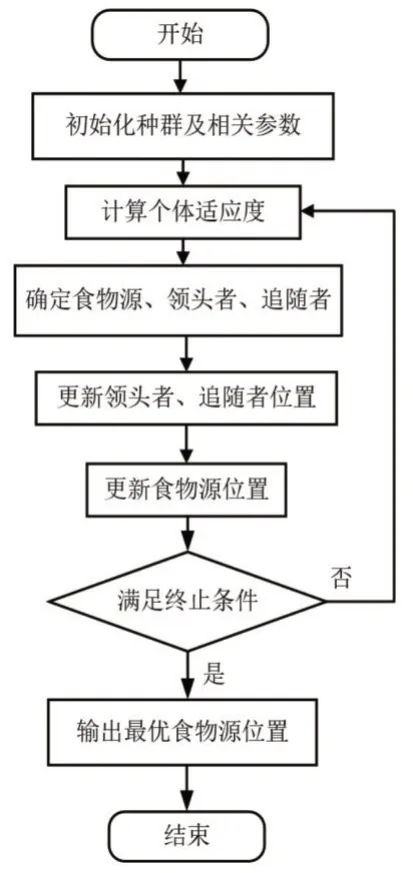
图2 樽海鞘算法流程

2 模型参数辨识

2.1 开路电压实验

实验对象为宁德时代NCM811 三元锂电池，其标称容量为40 Ah，充放电截止电压为2.75～4.2 V。选用ITECH 公司生产的ITS5300 系列电池测试系统进行实验，完成数据采集，如图3 所示。

图3 动力电池测试系统

OCV-SOC曲线标定实验步骤为：①使用标准的恒流恒压充电方式将电池充至满电状态，静置2 h。②以1/3C的恒定电流对电池进行放电，每次放10%的电池最大可用容量并静置1 h，静置后得到的端电压值视为OCV值。③循环步骤②直至电池的电量被放空。④记录实验过程中OCV与SOC数据。

在MATLAB 中使用polynomal 函数拟合OCV-SOC曲线的6 次多项式为：

2.2 FFRLS 在线参数辨识

FFRLS 通过引进遗忘因子来削减旧数据所提供的信息量，以提升算法后期自适应修正的能力。在进行参数辨识过程中，将电池模型看作以工作电流I(t)为输入，端电压U(t)为输出的单输入输出系统。通过分析电池模型，建立并求解系统的状态方程，进而推导出等效电路模型的电容和电阻参数。

令y(k)=Uoc(s) -Ut(s)，得一阶RC和二阶RC模型在频域下的差分方程为：

式中：a1、a2、a3、a4、a5、a6、a7、a8为相应系数；yfrist(k)和ysecond(k)分别代表一阶和二阶模型的电势差。

将系统考虑成一种外源性自回归模型，设系统k时刻的误差eLS,k为平稳零均值白噪声误差。系统输出变量yk可表达为：

式中：φk为系统数据矩阵；θk为系统待辨识参数矩阵。

FFRLS 利用输出与期望之间的误差和更新的量测值进行递归运算，对估计结果进行自适应修正，使系统取得最小目标函数。目标函数J(θ)为：

式中：l 为遗忘因子，本文取值为0.98。

当且仅当J(θ)导数为0 时，目标函数取最小值。则令J(θ)′=0，可解得最优参数矩阵θk为：

考虑FFRLS 算法协方差矩阵PLS,k=R－1k，可得：

式(17)中，系统增益矩阵KLS,k为：

式(19)中，系统估计误差eLS,k为：

HPPC 工况实验下一阶和二阶ECM 电阻、电容参数的辨识结果分别如图4、图5 所示。

图4 HPPC工况下一阶ECM电阻、电容参数辨识结果

图5 HPPC工况下二阶ECM电阻、电容参数辨识结果

3 模型切换仿真及实验验证

3.1 模型切换仿真

为验证本文所提出最优BIC 准则的有效性，将其在MATLAB 中进行仿真。验证工况为快速脉冲放电(使用1C电流放电，每放10%SOC电量后搁置1 h，以此循环至电量放空)，实验共计用时36 900 s。仿真SOC区间为90%～10%，用时31 680 s。BIC与最优BIC的模型切换效果仿真如图6所示。

图6 快速脉冲放电工况下基于BIC、最优BIC切换效果与切换模型端电压对比

分析图6(a)、(b)、(c)得，模型切换阶数与时间一一对应。分析图6(d)、(e)得，BIC 切换模型端电压与最优BIC 切换模型端电压逼近实验值。当时间处于3 960～3 976 s 时，最优BIC切换模型端电压误差明显小于BIC 切换模型。分析图6(c)、(d)、(e)得，在3 960～3 976 s 时，BIC 切换模型处于二阶状态，最优BIC 切换模型处于一阶状态，且最优BIC 切换模型端电压误差小于BIC 切换模型，说明此时一阶模型精确度高于二阶，最优BIC 切换模型复杂度与计算量均小于BIC 切换模型，凸显了最优BIC 下模型的精度与实用性。

由表2 可知，快速脉冲工况下，最优BIC 切换模型误差各项指标均低于BIC 切换模型。BIC 切换模型与最优BIC 切换模型端电压误差均值分别为0.012 4 和0.011 7 V，均方根误差分别为0.018 7 和0.016 6。实验结果表明，快速脉冲工况下，相比于BIC 切换，最优BIC 切换下的模型端电压误差较小，证明了切换模型的准确性与有效性。

表2 快速脉冲工况下BIC与最优BIC切换模型输出端电压误差统计分析

3.2 实验结果对比

为验证AVO 模型在HPPC 工况下的精度与实用性，将HPPC 工况实验得到的端电压、MATLAB 中使用FFRLS 得到的AVO 模型仿真端电压与使用FFRLS 得到的一阶和二阶ECM 的仿真端电压进行对比分析，结果如图7 所示。

图7 HPPC工况下AVO模型与一阶和二阶ECM端电压对比图

分析图7 可知：在短时间大电流充放电时，端电压急剧跳动，AVO 模型能够迅速响应，使模型端电压快速收敛至实验值附近，说明模型有较强的抗干扰性。在恒流放电过程中，模型端电压值与实验值逼近，误差基本保持在0.01 V 左右，说明模型能够根据电池工作状态很好地拟合出实验端电压值。在电池静置时，模型端电压值逼近实验值，说明模型能精确地反映电池的电压回弹特性。总体实验过程中，AVO 模型端电压与实验端电压保持了较好的一致性，亦验证了最优BIC 切换模型的精度与实用性。

详细误差统计分析如表3 所示。

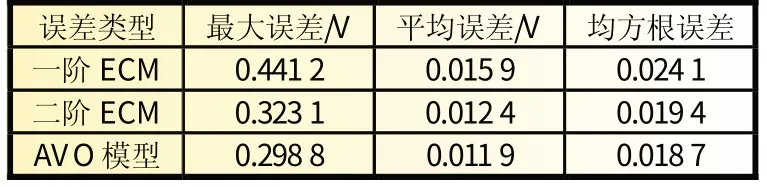
表3 AVO模型与传统一阶和二阶ECM端电压误差统计

由表3 可得：相较于传统一阶和二阶ECM，AVO 模型的最大误差分别降低了26.77% 和7.52%，平均误差降低了22.01%和4.03%，均方根误差降低了19.50%和3.61%，证明该模型精度与实用性较高。

4 结论

(1)利用樽海鞘算法对引入模型端电压误差平方和及惩罚系数改进的Bayes 信息量准则的参数进行优化，可保证AVO 模型实时处于最优阶数。

(2)快速脉冲工况实验下，BIC 切换模型的端电压均方根误差与平均误差分别0.018 7 和0.012 4 V，最优BIC 切换模型的此两项误差分别为0.016 6 和0.011 7 V，均小于BIC 切换模型，说明最优BIC 切换模型精度较高。

(3)HPPC 工况实验下端电压预测仿真表明，AVO 模型的各项误差均小于传统的一阶和二阶ECM；AVO 模型的平均误差为0.011 9 V，较传统一阶和二阶ECM 模型分别降低了22.01%和4.03%。