基于多模型融合的锂离子电池SOC自适应估计
吴逸洲,刘 艳,祝现染,王译萱
(1.华东光电集成器件研究所,江苏苏州 215000;2.北京理工大学,北京 100089)
锂离子电池是目前电动汽车行业广泛采用的储能元件。电动汽车的电池荷电状态(SOC)相当于燃油车的油量,可用于实时监控电池状态,避免车辆在行驶过程中的故障发生。由于无法对电池的SOC进行直接测量,研究者通常采用参数估计的方法确定SOC。电池在实际使用过程中的环境复杂,受到温度、阻抗和放电倍率等多种因素的影响,涉及参数繁多,使SOC准确估计的难度较高。
基于锂离子电池的容量衰减分布规律,建立电池容量衰减模型,能够提升参数数据较少时的电池容量预测能力。在电池容量预测的相关研究中,国内外学者就电池容量衰减模型开展了一系列试验研究。例如,黎火林等[1]对不同温度和放电倍率开展了电池寿命加速试验,表明随着电池充放电循环次数的增加,电池容量分布符合幂函数规律。Liaw 等[2]从温度和SOC的参数出发,对电池加速寿命试验进行设计,发现与温度相关的阻抗、功率和额定容量的变化符合Arrhenius公式。Atalay 等[3]根据P2D 模型,开发了一种基于SEI 膜生长和负极析锂的寿命衰降模型,该模型能够对电池的循环寿命衰降和寿命末期的跳水现象进行准确预测。综上,在国内外有关电池容量衰减模型的研究中,大多基于恒定条件下的电池加速寿命试验数据,对电池容量衰减进行拟合,但在实际的电池应用中,预测精度会随着电池的老化逐渐降低。因此,迫切需要考虑电池老化现象,对电池容量衰减进行更加准确的估计。
电池循环和存储过程中的衰降是锂离子电池容量衰减的主要来源[4]。为对锂离子电池循环导致的衰减进行模型搭建,本文采用FFRLS 算法进行模型参数的在线辨识,并形成了动力电池SOC的估计方法。结合电池加速老化试验数据,建立了动态应力下的电池容量衰减模型,更加准确地对电池SOC进行预测。最后,采用自适应卡尔曼滤波算法,建立了自适应SOC估计模型,以提高该模型对不精确SOC初值的修正能力。
1 电池试验
本文采用锰酸锂电池单体作为试验对象,该电池额定容量为45 Ah,充放电截止电压为3.0~4.2 V。试验设备为FTF2-500/50-750 型动力电池测试系统和EWER-A3-40-CP-AR 型步入式环境舱。通过必测系统上位机编辑了静态容量试验、混合脉冲特性和开路电压试验。
2 电池模型
2.1 等效电路模型
He 等[5]发现,DP 等效电路模型对电池的预测精度性能最佳,其动态电压特性可等效为图1 所示,包括开路电压Uoc、2条RC 网络和电阻R0。图中:R0模拟电压突变的电阻特性;Rd、Cd分别表征由浓差极化的电阻和电容;Rc、Cc表征由电化学极化的电阻和电容。

图1 等效电路模型
该模型的状态方程如下:
式中:Ut为电池电压;Ud、Uc分别为Rd、Rc电压;IL为充放电流。
2.2 在线参数辨识
采用遗忘因子递推最小二乘法(FFRLS)实现参数在线辨识,可有效解决因参数变化慢导致的参数估计不准的问题[6]。为避免递推发生“数据饱和”,本文设置遗忘因子l,具体算法流程如图2 所示。
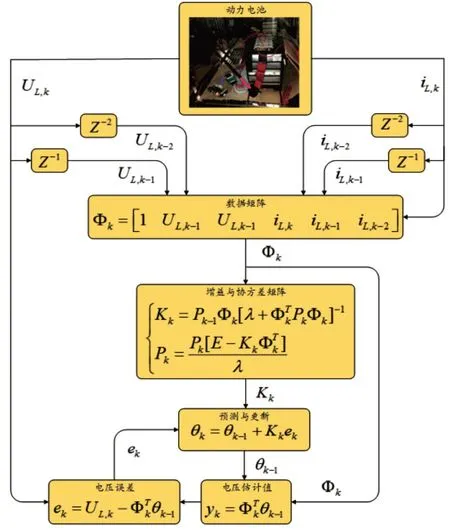
图2 基于FFRLS方法的电池模型参数在线辨识流程
电池模型转化如下:
式中:ek为零均值白噪声;θk为参数矩阵;Φk为数据矩阵。
对式(1)进行拉普拉斯变换:
采用欧拉法将上式离散化,变换公式为:
其中T为采样间隔时间,代入式(4)中,可得到:
对式(5)进行z反变换,得到差分方程:
由于采样时间T较小,在T时间内开路电压Uoc基本无变化,故:
式(6)可简化为:
得到电池模型输出矩阵yk、参数矩阵θ和数据矩阵Φ:
2.3 电池容量衰减模型
2.3.1 恒定应力下的电池容量衰减模型
电池每次循环充放电都会造成微小的容量损失ΔC,经t次循环,电池累积容量衰减量为x(s,t)。由中心极限定理可知,当t足够大时,x(s,t)近似正态分布[7],即电池容量的衰减过程为高斯过程。因此电池在应力s下的容量衰减服从如下正态分布:
式中:u(s,t)和σ2(t)分别为在应力水平s下,电池循环t次后的容量衰减量均值和容量衰减量方差。
从统计学的角度考虑,应按照加速老化试验的数据,对动力电池的容量衰减量进行最大似然估计,并取容量衰减量均值u(s,t)的估计值作为预测模型的特征值。将u(s,t)进行曲线拟合与回归分析,得到电池的容量衰减方程式:
式中:s为应力类型;hi(s)为常数。当应力s分别选择温度T和放电倍率Rd时,i=1,2。
本文以恒定小倍率电流充电,故不考虑充电倍率的影响。
2.3.1.1 基于温度应力的容量衰减模型
参考Matthieu 等[8]提出的阿伦尼乌斯模型,列出衰减方程系数:
式中:k、F为与应力及时间无关的常数;T为绝对温度。
令G=lnk,则:
由式(11),得到容量衰减模型:
将上式数据进行拟合,得到参数G、F和h1(T)的值。
在20 和40 ℃下,电池容量的衰减情况如表1 所示,电池循环300 次的容量衰减拟合结果见图3。

表1 不同温度下的电池容量衰减情况(0.5 C 充电,1 C 放电)

图3 20和40 ℃下的电池容量衰减拟合曲线
根据式(14)和图3 的拟合结果,得到如下公式:
对上述方程进行求解,得到F=-433 0.2,G=17.4,则电池在温度应力下的衰减方程为:
2.3.1.2 基于放电倍率应力的容量衰减模型
在加速寿命试验中,作为加速的电应力一般服从逆幂律关系[9]:
式中:ξ为寿命特征值;A为正常数;ν为电应力;c为与激活能有关的正常数。
由容量衰减方程式(11),可得到动力电池的平均寿命L:
式中:l为失效阈值,即实际容量衰减为初始值的80%。
当ξ作为电池寿命的平均值时,D=为正常数,c=chi(ν)是与激活能相关的正常数。将放电倍率设为加速应力,代入上述公式进行推导,得到Rd的容量衰减模型为:
式中:D、c、E和h2(Rd)均为常数。
根据电池加速寿命试验,得到循环300 次的电池容量衰减情况,如表2 所示。根据表2 的数据,得到图4 所示的1C、2C和3C下的循环次数与电池容量衰减拟合曲线,衰减方程参数如表3 所示。

表2 1 C、2 C 和3 C 下的电池容量衰减情况

表3 1 C、2 C 和3 C 下的电池容量衰减方程参数

图4 1 C、2 C和3 C下的电池容量衰减拟合图
令h2(Rd)≈0.79。对衰减参数进行拟合,得到电池容量衰减方程系数曲线,如图5 所示,其表达式为:

图5 不同放电倍率的容量衰减参数曲线
根据式(19),得到电池模组在不同放电倍率下的衰减方程,即:
2.3.1.3 复合应力下的容量衰减模型
在上述模型中增加温度应力的加速衰减因子,本文建立了复合应力下的容量衰减模型。温度应力的Ⅱ型加速衰减因子与时刻t无关[10],即:
将式(22)中的温度分别取T1=T0、T2=T,则可得到在(T,Rd)应力条件下的电池容量衰减模型,即:
则式(23)可写成:
根据式(16)和式(22),可得到容量加速衰减因子,即:
根据式(21)和式(26),可得到在(T,Rd)应力条件下电池容量的衰减模型,即:
2.3.2 动态应力下的电池容量衰减模型
上述三种电池容量衰减模型是通过300 次电池循环数据拟合所得,因数据量较少,其预测性能随电池的老化而变差。由于车辆行驶过程中的动力电池并非以恒流工作,而是按功率放电,因此,当电池容量衰减时,内阻也随之增大,导致电压平台变低。为满足同功率输出,需提高放电电流,即放电倍率伴随容量衰减有增大趋势。由此,本文建立了动态应力下的电池容量衰减模型,以提高电池容量衰减预测的精确性[11]。
由于动力电池的容量衰减呈非线性,电池每轮衰减度受到单次循环最大有效容量的影响。基于实时电池容量状态的动态应力,本文构建了容量衰减模型。记ut(T,Rd)为t次循环时的容量衰减量,ut+1(T,Rd)为t+1 次循环时的容量衰减量,则有:
式中:ut+1(T,Rd)为t轮循环后的电池容量衰减量,表示在(T,Rd)的作用下,第t+1 轮循环后的衰减总量;ut(T,Rd)为t轮循环后的电池容量衰减总量,与t-1 轮的衰减量及应力水平相关。
记Ti、Rd,i分别为第i轮循环时的应力,则公式(28)可以转化为:
进一步可以得到经过m轮循环后的衰减量ut+m(Tt+m,Rd,t+m),即:
根据本研究开展的加速寿命试验的电池拟合系数,得到电池容量衰减系数方程:
由容量衰减模型公式(30)和衰减系数方程(31),推导出第t-1 轮循环后的最大有效容量Ct的预测模型如下:
Ti、Rd,i的取值方式如下:由于温度变化相对较慢,设定电池温度采集频率为0.01 Hz,Ti为i轮循环中采集温度的平均值;由于放电倍率并非恒定,设定放电电流采集频率为1 Hz,将i轮循环中放电电流平均值与额定容量的比设定为Rd,i。
3 基于多模型融合的自适应SOC 估计
本文采用自适应卡尔曼滤波算法(AEKF),对模型参数及噪声统计特性进行修正,以提高SOC的预测精度[12],使之具有更好的环境适应性。计算流程如下:
首先,对动力电池充电状态SOC进行离散化,可转换为:
式中:z为电池充电状态;η为电池库仑效率;Δt为采样时间;C为电池最大有效容量。
其次,对动力电池等效电路模进行离散化处理,得:
由公式(33)和公式(34),可得到该离散系统中的状态转移矩阵与测量矩阵:
根据上述方程,建立动力电池系统状态方程和观测方程:
式中:x=[z Ud Uc]T。
最后,通过结合电池模型参数FFRLS 算法、电池容量衰减模型及自适应卡尔曼滤波算法,建立基于多模型融合的自适应SOC估计算法,具体计算流程如图6 所示。
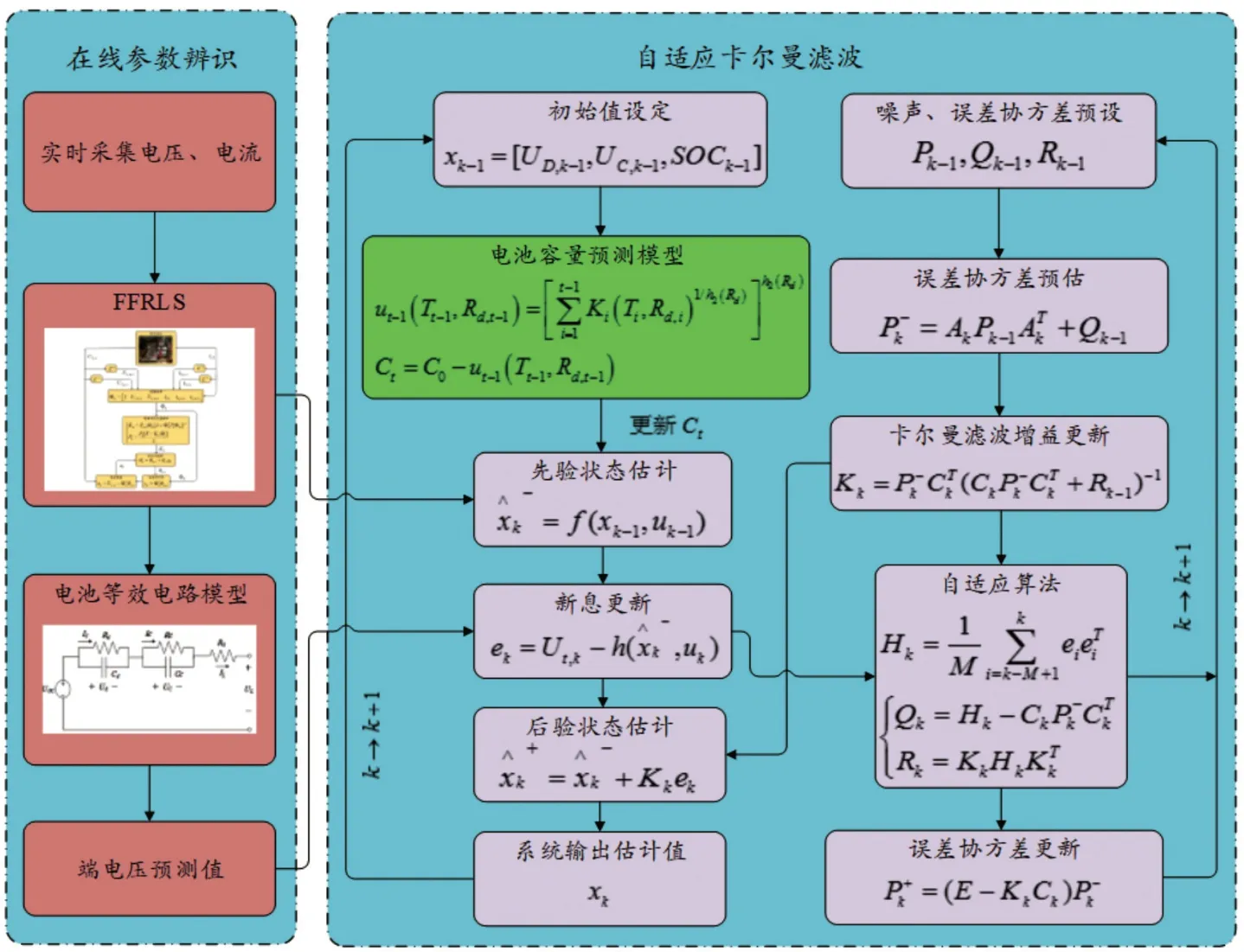
图6 SOC估算流程
4 SOC 估计算法的仿真与评估
在25 ℃下,电池以城市道路循环(UDDS)工况在90%~20%的SOC区间进行循环充放,每循环5 次进行一次定容,共循环600 次,以第600 次循环数据进行仿真分析。图7(a)为电池实际容量衰减曲线和预测容量衰减曲线,图7(b)表明本文所提出的电池容量衰减模型能够较准确地预测电池容量的衰减过程,预测误差小于1.5%。

图7 工况循环下电池实际容量衰减与模型预测对比
图8(a)是电池第600 次循环中实际SOC参考值曲线和模型估计SOC曲线,可以看出,电池容量更新后的SOC估计曲线与参考值曲线基本吻合。图8(b)结果显示,初始SOC误差在10%的情况下,SOC估计能迅速收敛至真值附近,且能保持SOC估计误差在1.5%以内。以上结果表明,本文提出的基于电池容量模型的SOC自适应估计算法,在电池容量的预测方面具有很好的鲁棒性和较高的估计精度。

图8 600次循环电池实际SOC曲线与模型估计对比
5 结论
基于锂离子电池容量衰减的分布规律,本文首先建立了电池等效电路模型,并采用FFRLS 算法对模型参数进行在线辨识,以提高模型预测电压的精度。然后基于加速寿命试验数据,建立了恒定应力下的电池容量衰减模型,考虑到电池使用状态的不稳定性,为了更好地模拟电池容量的实际衰减过程,基于当前电池的容量状态,建立了动态应力下的电池容量衰减模型。最后根据电池等效电路模型、电池容量衰减模型和自适应卡尔曼滤波算法,提出了基于电池容量模型的自适应SOC估计方法,更好地实现电池SOC的精确估计。经过仿真分析与评估,表明本文所提出的方法能够实现电池容量和SOC的较准确估计,该算法具有很好的鲁棒性和可靠性。

