基于改进黏菌优化算法的光伏多峰MPPT控制策略

董 密,胡佳盛,杨 建,宋冬然,万江湖

(中南大学自动化学院,湖南长沙 410000)

1 引言

随着传统化石能源污染大、储量有限等问题的日益突出,新能源以其储量丰富、无污染、可持续等优点而备受关注.太阳能作为新能源中最重要的一环,光伏发电现已成为各种新能源发电中发展最迅速、规模最大的产业之一[1].

然而光伏电池的非线性输出特性使如何保持光伏系统工作在最大功率点处成为难题.为解决该问题,各种光伏最大功率点追踪(maximum power point tracking,MPPT)技术广泛运用于功率优化器设计中以提高光伏系统发电效率.传统的MPPT控制策略如扰动观测法(perturbation and observation,P&O)[2]和电导增量法[3]等在解决均匀光照强度下的单峰光伏模型时表现良好,然而在局部阴影遮挡条件(partial shading condition,PSC)下时,光伏系统的输出P-U特性曲线不再是单峰模型而是多峰模型,继续使用传统的MPPT控制策略容易陷入局部最优解,导致光伏系统发电效率降低[4].

为解决传统MPPT控制策略在PSC条件下容易陷入局部最优解的问题,国内外学者提出了一些适用于PSC 下的新型MPPT控制策略.这些策略根据控制方式的不同,可以分为离线型和在线型两种[5].离线型MPPT控制策略根据先验条件计算出光伏系统理想的数学模型,并在后台运用算法找出该模型的最大功率点实现离线控制,如文献[6]提出的基于灰狼优化算法的MPPT控制策略和文献[7]提出的基于多重双向PV-Cuk逆变器的MPPT控制策略.该类控制策略由于不需要反馈,故具有追踪速度快、稳态波动小等优点,但是,由于寻优过程在理想模型上进行,输出没有实时监控,故可靠性较低、通用性较弱.在线型MPPT控制策略则实时监控光伏系统的输出功率,根据功率的实时变化在线调整光伏阵列的输出电压,跟踪最大功率点,如文献[8]提出的基于粒子群算法(particle swarm optimization,PSO)的MPPT控制策略和文献[9]提出的基于风功率驱动算法的MPPT控制策略.该类控制方法不需要先验知识,具有实用性强、适用范围广、可靠性高等优点,但由于需要根据输出反馈调节,故调节时间较长、响应速度较慢.

无论是离线型还是在线型的MPPT控制策略都依赖寻优方法的全局搜索能力[10],而元启发算法正是针对大范围优化问题所提出的一种具有优秀全局搜索能力的新型高效优化方法[11],可以有效解决传统MPPT控制策略容易陷入局部最优解的问题.因此各种元启发算法诸如粒子群算法[8]、灰狼优化算法[6]、蚁群算法[12]等在MPPT控制策略的研究中得到了广泛应用.但上述算法的性能仍有一定改进空间[13].黏菌优化算法(slime mould algorithm,SMA)是一种新型元启发算法,其模拟黏菌的扩散和觅食行为,通过各项权值以及随机函数产生的搜索空间可以使黏菌以任意方向和任意步长进行寻优,具有全局搜索能力强的优点[14],然而其追踪速度还存在一定提升空间.

本文在传统SMA 算法的基础上提出了一种基于改进黏菌优化算法(improved SMA,ISMA)的在线型MPPT控制策略.该策略在传统黏菌优化算法的基础上结合光伏阵列的特性,改进了其边界条件,提高了算法的收敛速度;并且通过引入Lévy飞行策略,优化收敛准则,进一步提高算法的收敛速度,使其可以更加快速地追踪到整个光伏阵列的全局最大功率点,提高光伏系统发电效率.本文首先介绍了光伏阵列的数学模型,然后介绍了基于ISMA的MPPT控制策略,最后通过仿真和硬件实验验证该控制策略的优秀性能.

2 光伏电池建模及PSC下光伏阵列特性分析

2.1 光伏电池建模

光伏电池是整个光伏系统的核心部分.工程上常用理想模型或者单二极管等效电路模型来对其进行分析研究,其结构如图1所示.

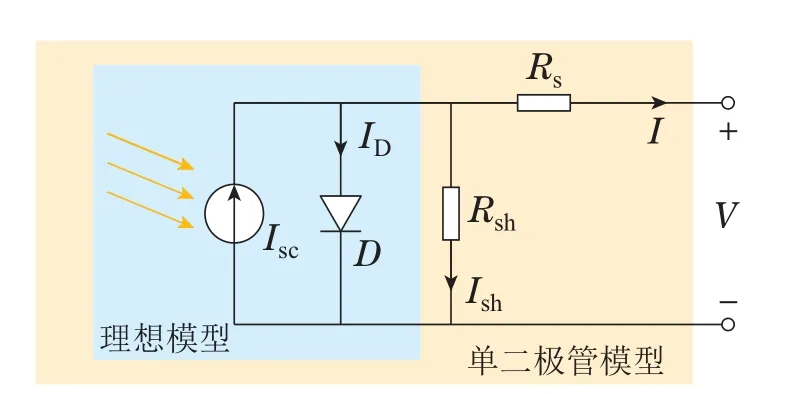
图1 光伏电池的等效结构图Fig.1 Structure diagram of photovoltaic cell

光伏电池单二极管模型的等效伏安特性方程可表示为

式中:Iph是光生电流,其大小随着温度和光照强度的变化而变化;ID为流过二极管D的电流;Ish为流过并联电阻Rsh的电流;I0是二极管D的反向饱和电流;q是电荷量、I和V分别为光伏电池的输入电流和输出电压;A是电池理想饱和因子;T是绝对温度;k是玻尔兹曼常数;Rs和Rsh分别是等效串联和并联电阻.

2.2 PSC下光伏阵列特性分析

本文以BIPRO TD7G72M 530W型号光伏组件为例,其在环境温度为25◦C、光照强度为1000 W/m2的标准测试条件(standard test conditions,STC)下的参数如表1所示.

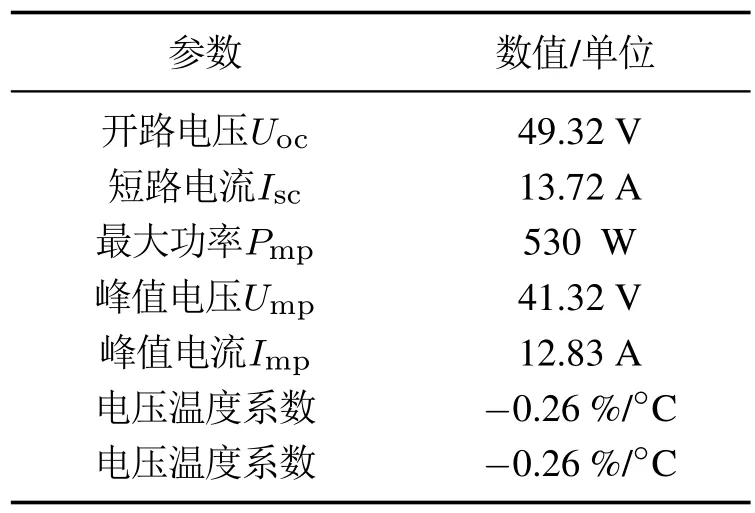
表1 光伏组件STC参数Table 1 Parameters of photovoltaic module under STC

本文选择如图2所示的3×3光伏阵列为研究对象.对于串联的光伏组件,一般串联单元并联一个旁路二极管防止反向电压[15].当上述光伏阵列中的9个光伏组件的温度为25◦C,光照强度分别为1000,800,500;1000,600,600;600,1000,1000 W/m2时,光伏阵列的输出I-U、P-U特性曲线如图3所示.

图2 3×3光伏阵列结构图Fig.2 Structure diagram of 3×3 photovoltaic array

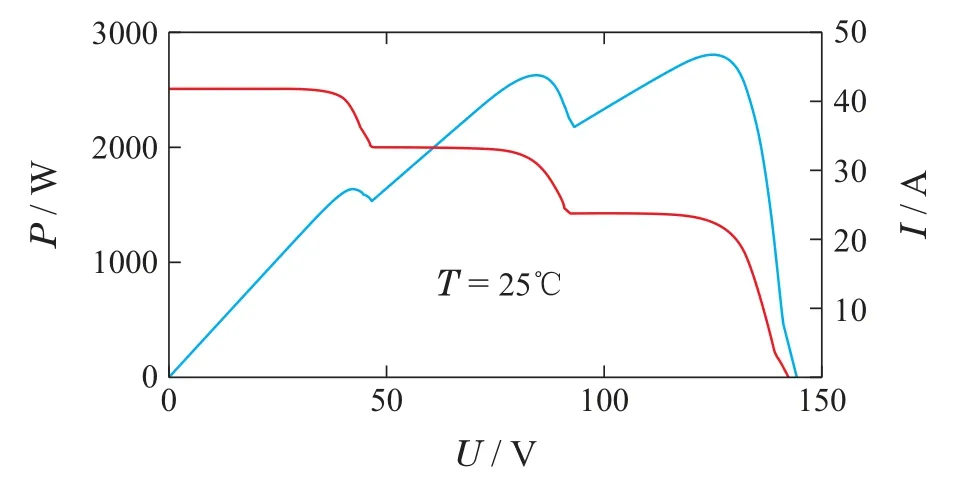
图3 PSC下光伏阵列的I-U和P-U特性曲线Fig.3 I-U and P-U characteristic curve of the photovoltaic array under PSC

3 基于ISMA的MPPT控制策略

3.1 黏菌优化算法(SMA)

黏菌优化算法是由Li等人于2020年提出的新型元启发优化算法,它模拟黏菌在觅食过程中的行为和形态变化,通过特殊权值-重量W的更新来模拟觅食过程中的正负反馈,从而根据黏菌重量W和黏菌适应度来改变觅食寻优步长,进而进行全局寻优.整个觅食寻优过程分为接近食物、包裹食物和振荡觅食3 个阶段[14].黏菌根据自身重量以及种群中所有黏菌的适应度来接近食物,它的逼近行为满足如下表达式:

式中:bF表示最佳黏菌适应度,wF表示最差黏菌适应度,r表示[0,1]间的随机数,N表示黏菌种群个数.

式(3)中,p表示选择概率,其满足

式中:S(i)表示第i个黏菌的适应度,DF表示所有代数中黏菌的最佳适应度.

3.2 改进的黏菌优化算法(ISMA)

传统SMA虽然具有较强的全局寻优能力,但是在解决光伏MPPT这一特殊问题时,一方面其边界条件容易导致部分超出边界的黏菌距离最佳适应度的位置较远,较难回归到最佳适应度位置,导致算法收敛速度降低;另一方面,当r≥p时,黏菌位置仅以指数形式减小,不利于全局寻优,具有一定的局限性.因此,本文在传统SMA的基础上提出新的边界条件,使其适应光伏阵列输出特性,提高算法的收敛速度;同时采用Lévy飞行策略改进其迭代过程的收敛准则,进一步提高其寻优性能.

3.2.1 边界条件

传统的SMA算法由于全局寻优能力的需要,在迭代前期,指数系数以及黏菌重量权重W都较大,这使得黏菌位置有较大可能在迭代过程中超出边界.而原算法边界条件的处理方法为:超出上边界的黏菌取上边界值,超出下边界的黏菌取下边界值[15],如式(7)所示,这种处理方法不利于算法的收敛.为了加速算法收敛、提高光伏系统发电效率,本文提出如式(8)所示的新的边界条件.该边界条件使得超出范围的黏菌在迭代次数较小、距离全局最优解较远时,黏菌受随机系数的影响较大,寻优空间也较大,增强其全局搜索能力;当迭代次数较高、距离全局最优解较近时,黏菌受随机系数的影响较小,受最佳适应度位置的影响较大,黏菌得以更快速地向最佳适应度位置附近靠拢,使得算法局部搜索能力更强、更容易收敛.

式中:UB表示取值上界,LB表示取值下界.

式中a1,a2为调节常数.

3.2.2 基于Lévy飞行的逼近准则

Lévy飞行是由Paul Pierre提出的一种随机游走过程,其特征是在多数的小步长移动中穿插大步长移动,该方法可以有效的提高系统全局搜索能力[16],其公式定义为

即当r≥p时,相比于原SMA算法的黏菌位置按照指数形式依次减小,新的收敛准则使得黏菌位置在Lévy飞行的基础上按照指数减小.新的收敛准则不但增加了迭代次数较小时的搜索空间的随机性,提高了算法的全局搜索能力,而且可以保证其在迭代次数较大时有较强的局部搜索能力,提高了算法收敛速度,使得光伏系统能够更快速追踪到全局最优解.

将改进后的ISMA算法和传统SMA算法在F(x)=两个测试函数下进行比较,其适应度变化曲线如图4所示.由图4可以看出ISMA算法在收敛精度和收敛速度上均比SMA算法更加出色.

3.3 基于ISMA的MPPT控制策略

为将该ISMA算法应用于MPPT控制策略,需对其进行如下初始设计.

3.3.1 黏菌位置初始化

3.3.2 算法终止条件设计

为了使算法在寻找到全局最大功率点后结束迭代、使光伏系统稳定工作在最佳工作点,该算法在满足下述任意终止条件时停止迭代:

1)当迭代次数到达设定的最大次数时,即满足下式时停止迭代:

该条件表示,若算法在预设迭代次数内仍未找到全局最优解,为避免陷入死循环,直接终止算法.

该条件表示,若所有黏菌足够集中,即全部黏菌收敛到一个很小的区间,表示算法寻找到全局最优解,可以终止算法.

3.3.3 算法重启条件设计

当外部光照温度条件或者遮挡情况发生变化时,需重启算法,改变光伏系统的工作状态以适应光伏阵列输出特性的变化,本文设计算法重启条件如下:

式中:Preal表示光伏阵列的实时输出功率,Pm表示稳定工作时的输出功率.即当光伏系统稳定工作时,如果实时输出功率改变量大于10%时,系统判定外部环境条件发生变化,需要重新启动MPPT控制策略寻找新的最大功率点.

综上,基于ISMA的MPPT控制策略流程图如图5所示.

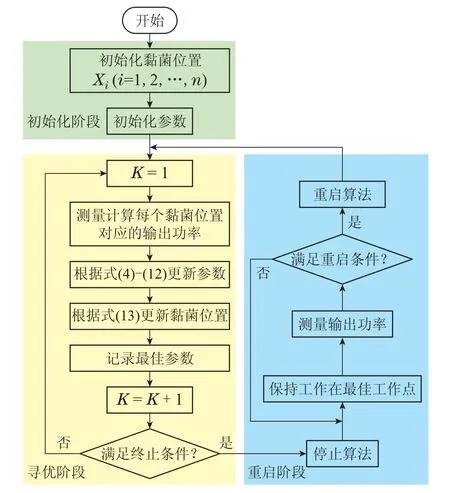
图5 基于ISMA的MPPT控制策略流程图Fig.5 Flow chart of ISMA based MPPT

4 仿真分析

为了验证该基于ISMA的MPPT控制策略的可行性,本文在MATLAB/Simulink仿真平台上建立如图6所示的光伏系统进行研究.该光伏系统主要由光伏阵列、BOOST升压电路、MPPT 控制电路和负载4大部分组成.其中光伏阵列部分由上述的BIPRO TD7 G 72M 530W型号光伏组件按照3×3的形式组成;BOOST 升压电路部分参数选择如下:Cin=400µF,L=30 mH,C=80µF;负载部为30 Ω 的纯电阻负载.为了验证该基于ISMA 的MPPT 控制策略的优越性能,将其与基于SMA,PSO和P&O的MPPT 控制策略分别在如表2所示的3种不同的光照条件下进行仿真比较,且环境温度均为25◦C.

表2 光伏系统的3种光照条件Table 2 Three illumination conditions of PV system

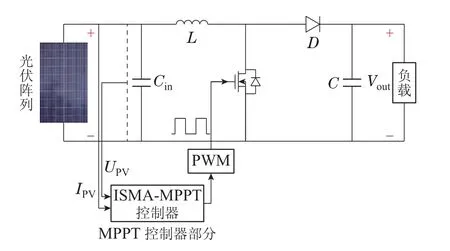
图6 光伏系统结构图Fig.6 Structure diagram of photovoltaic system

4.1 无阴影条件下的仿真结果

光伏阵列在无阴影遮挡条件下时,仿真条件设置为STC,则基于4种MPPT控制策略的光伏系统输出功率仿真波形分别如图7(a)-(d)所示.

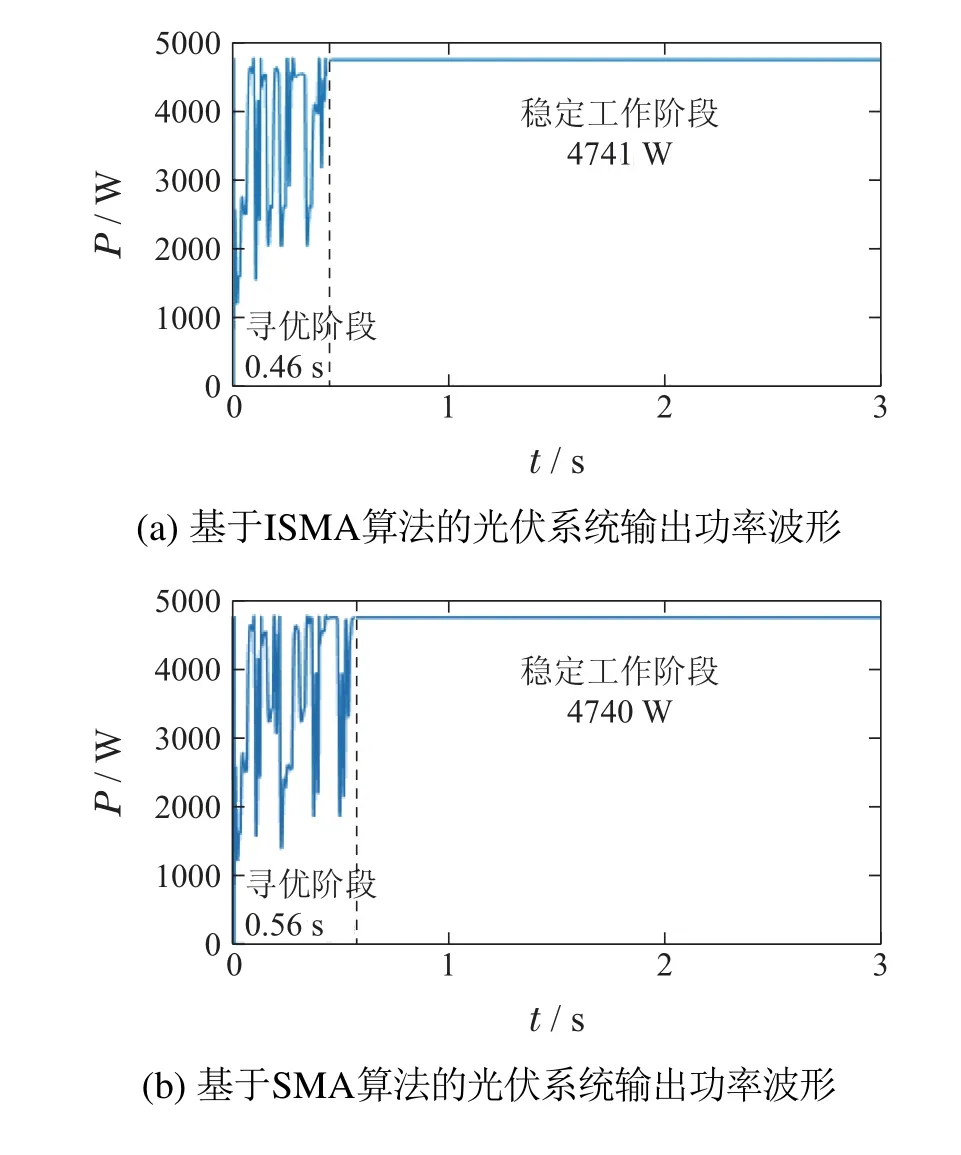
图7 无阴影遮挡条件下光伏系统输出功率波形Fig.7 Output power waveform of PV system without shadow

由图7可知,在该条件下,4种算法均可追踪到该光伏系统的实际最大功率4770 W附近,具体工作情况如表3 所示.P&O 算法用时0.04 s 就到达最大功率4740 W,功率损耗为0.63%;SMA 和PSO 算法分别用时0.56 s 和1.72 s 到达最大功率,功率损耗分别为0.63%和0.65%;ISMA 算法相较于前两种算法在追踪速度和追踪精度上更好,用时0.46 s 到达最大功率4741 W,功率损耗为0.61%,相较于SMA 和PSO 算法提高了约17.86%和73.26%的追踪速度.

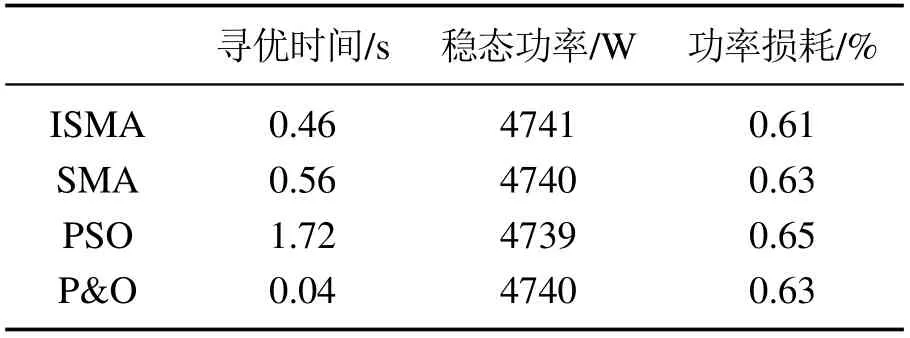
表3 无阴影条件下4种MPPT控制策略的工作情况Table 3 Performance of 4 methods without shadow

4.2 局部阴影遮挡条件下的仿真结果

光伏阵列在阴影遮挡条件1下时.采用基于4种算法的MPPT控制策略的光伏系统输出功率仿真波形分别如图8(a)-(d)所示.

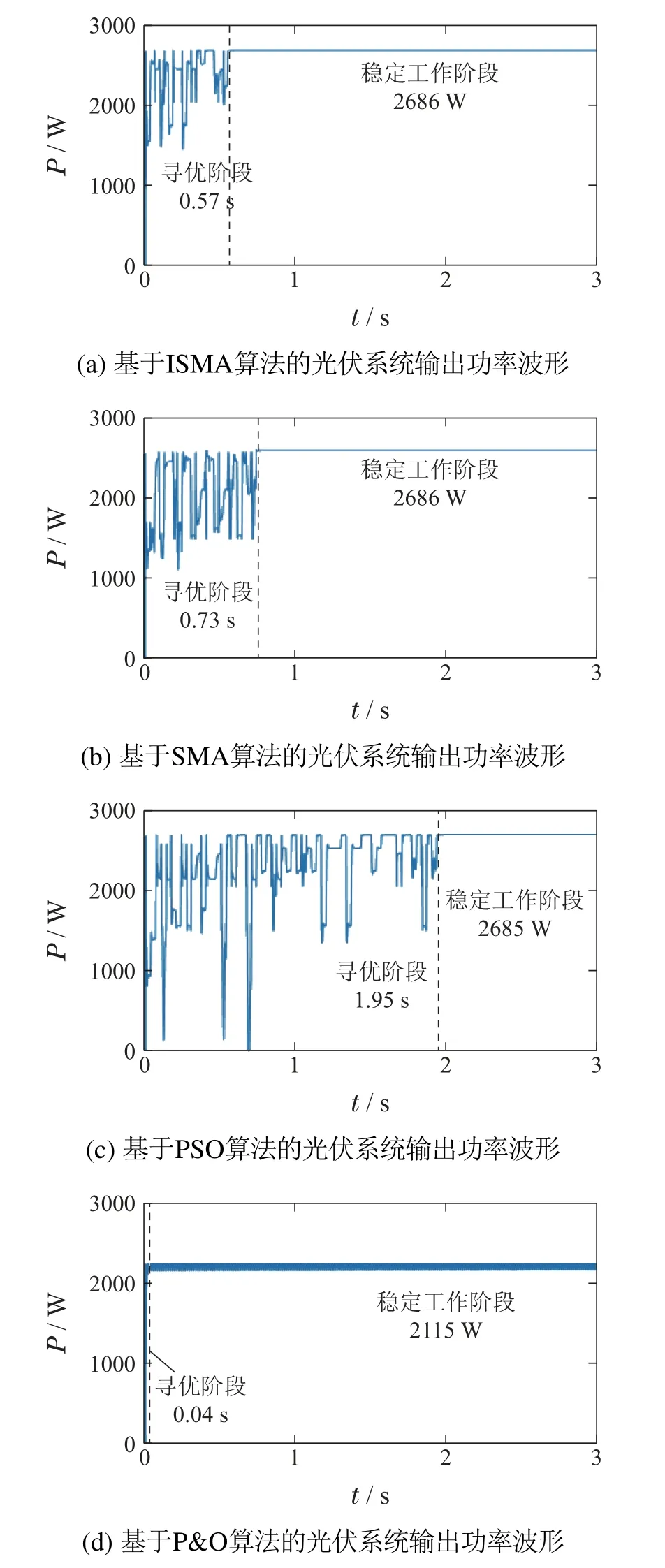
图8 部分阴影下光伏系统输出功率波形Fig.8 Output power waveform of PV system under PSC

由图8可知,在局部阴影遮挡条件下,基于ISMA,SMA和PSO的MPPT控制策略都可以追踪到该光伏系统的实际最大功率2712 W附近,但是P&O算法在到达局部最优解附近便停止工作,未追踪到全局最大功率点,4种算法的工作情况如表4所示.SMA和PSO算法分别用时0.73 s和1.95 s到达最大功率点,功率损耗分别为0.96%和0.99%;ISMA算法则仅用时0.57 s到达最大功率2686 W并维持稳定,功率损耗约为0.96%,相较于SMA和PSO算法提高了21.92%和70.77%的追踪速度.

表4 局部阴影下4种MPPT控制策略的工作情况Table 4 Performance of 4 methods under PSC

4.3 变化的阴影遮挡条件下的仿真结果

光伏阵列处于变化阴影遮挡条件下时,光照强度由阴影遮挡条件1变化为阴影遮挡条件2,采用基于4种算法的MPPT控制策略的光伏系统输出功率仿真波形如图9(a)-(d)所示.

由图9可知,在该条件下,基于ISMA,SMA和PSO的MPPT控制策略均可追踪到该光伏系统的最大功率点附近,并当遮挡条件改变时也能及时重启算法到达新的最大功率点,而P&O 算法则会陷入局部最优解.4种算法的工作情况见表5.SMA算法用时0.59 s左右到达阴影遮挡条件1的最大功率2684 W,功率损耗约为1.03%,并用时0.91 s追踪到新的最大功率3290 W,功率损耗约为1.02%;PSO算法用时1.53 s左右到达阴影遮挡条件1下的最大功率2685 W,功率损耗约为0.99%,并用时1.58 s追踪到新的最大功率3290 W,功率损耗约为1.02%;而ISMA仅用时0.43 s左右便到达阴影遮挡条件1下的最大功率2684 W,功率损耗约为1.03%,并用时0.50 s追踪到新的最大功率3291 W,功率损耗约为0.99%,较于SMA和PSO提高了约32.00%和70.09%的追踪速度,且功率损耗更小.

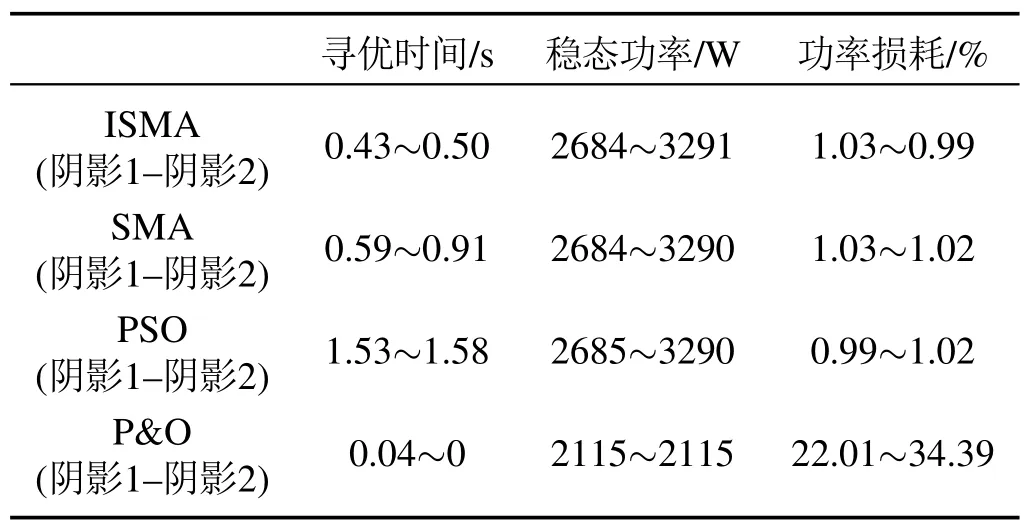
表5 变化阴影下4种MPPT控制策略的工作情况Table 5 Performance of 4 methods under varying shading condition

5 实验验证

为进一步验证所提出的基于ISMA的MPPT控制策略的可行性,搭建如图10所示的光伏实验平台,其主要由光伏阵列、光伏功率优化器和负载3大部分组成.其中光伏阵列部分由3×3 的XKD-30W型号光伏组件组成,每个光伏组件的参数如表6所示;光伏功率优化器集成在基于“进芯”ADP32F10A型号芯片的开发板上,由BOOST电路部分和基于ISMA算法的MP PT控制器部分组成;负载选用30 Ω恒阻值负载.

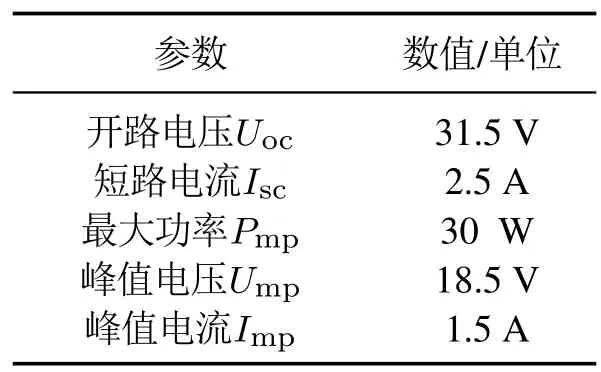
表6 光伏组件STC参数Table 6 Parameters of photovoltaic module under STC

图10 光伏实验平台Fig.10 Photovoltaic experimental platform

实验分别在无阴影条件和PSC条件下进行,光伏阵列在这两种条件下的输出P-U曲线如图11所示.采用基于P&O和ISMA算法的光伏系统在这两种条件下的输出电压、电流和功率波形分别如图12-13所示.电压和电流信号均采用×10档位表笔测量.

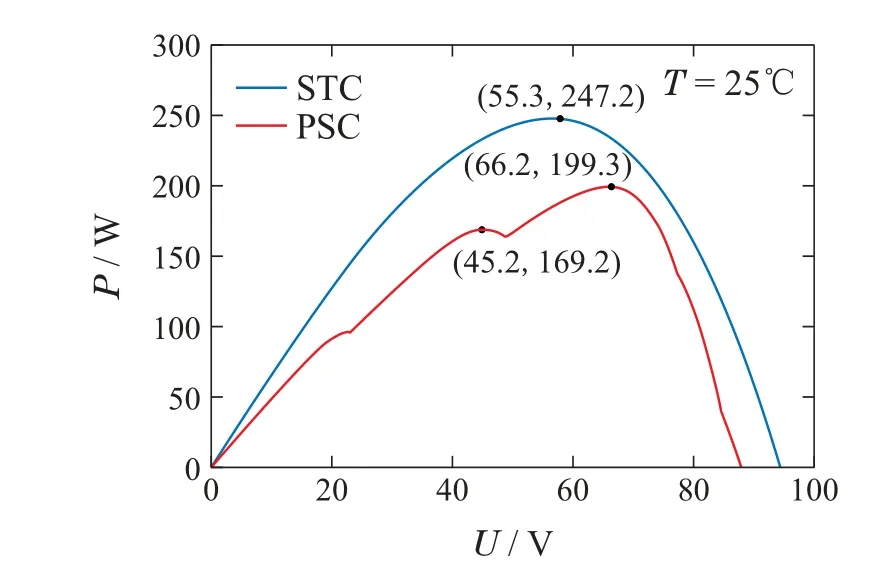
图11 光伏阵列在两种光照条件下的输出P-U曲线Fig.11 Output P-U curve of PV array under two illumination conditions

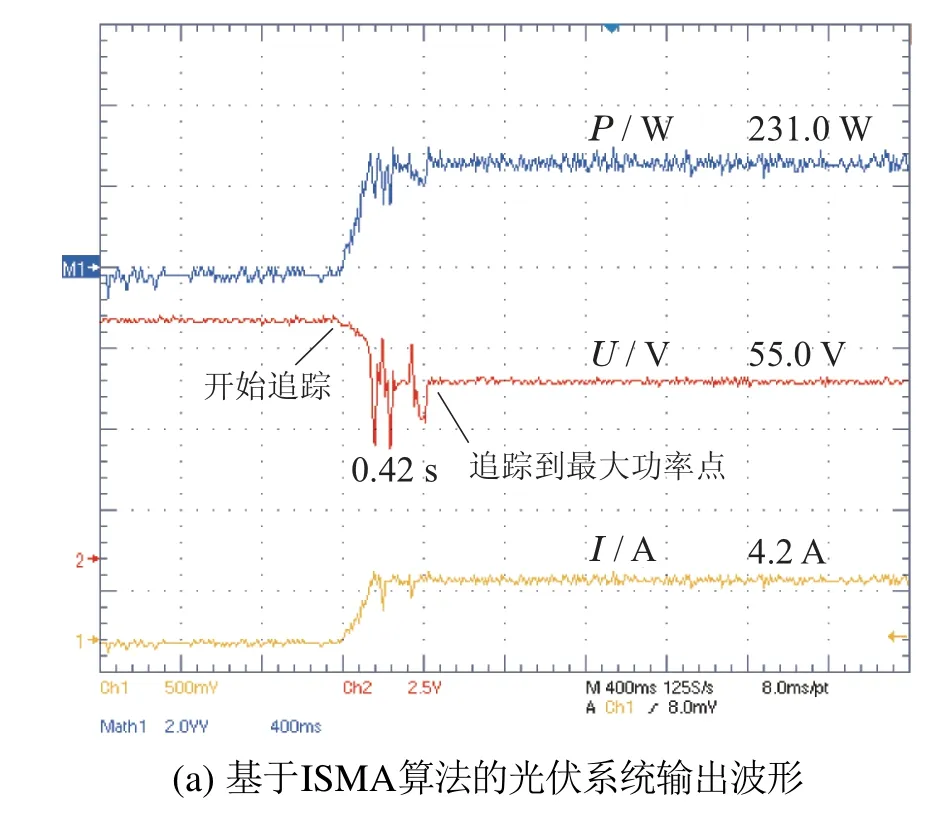
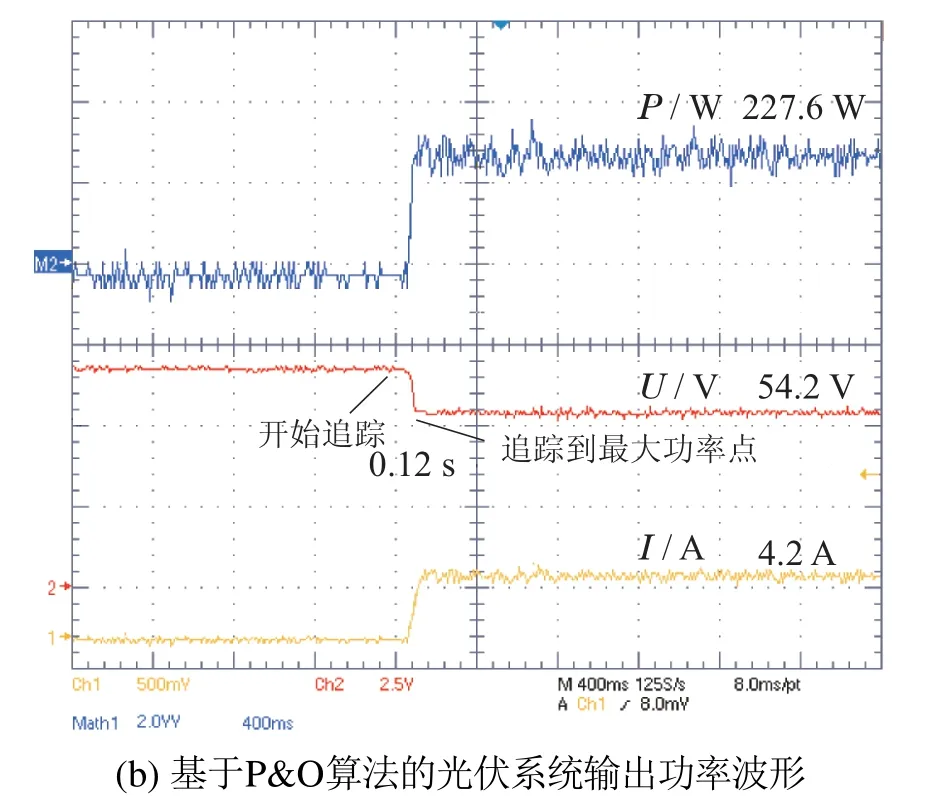
图12 无阴影遮挡下光伏系统的输出波形Fig.12 Output waveform of PV system without shadow

由图12可知,在无阴影遮挡条件下,ISMA算法和P&O算法都可以跟踪到最大功率点(55.3 V,247.2 W)附近.其中P&O算法追踪速度更快,仅用时0.12 s便追踪到最大功率点,此时光伏系统输出电压约为54.2 V,输出功率约为227.6 W,功率损耗约为7.93%;ISMA算法则稳态精度更高、功率损耗更小,用时0.42 s到达最大功率点,光伏系统的输出电压约为55.0 V,输出功率约为231.0 W,功率损耗仅约为6.55%.

由图13可知,在局部阴影遮挡条件下,ISMA算法可以跟踪到最大功率点(66.2 V,199.3 W)附近,而P&O算法陷入了局部最优解.其中P&O算法用时0.10 s到达局部最大功率点,光伏系统的输出电压约为44.5 V,输出功率仅约为169.0 W,功率损耗高达15.21%;而ISMA算法则用时0.72 s到达全局最大功率点,光伏系统的输出电压约为65.1 V,输出功率约为198.5 W,功率损耗仅约为0.35%,相较P&O算法降低了14.86%的功率损耗,展现出更好的性能.

综上,所设计的基于ISMA算法的MPPT控制策略在无阴影遮挡和部分阴影遮挡条件下均可以快速准确追踪到光伏系统的全局最大功率点,极大地提高光伏系统的发电效率,具有充分的可行性.

6 结论

本文针对局部阴影遮挡条件下,光伏阵列的输出功率曲线呈现多峰模型时,传统MPPT控制策略容易陷入局部最优解的问题,提出一种基于ISMA的在线型MPPT控制策略.该控制策略在SMA的基础上,优化了其边界条件和收敛准则,提升了算法的全局搜索能力,提高了其追踪速度和追踪精度,使光伏系统的发电效率得到有效提高.通过仿真和实验结果分析可得如下结论:

1)所提出的基于ISMA的MPPT控制策略在无阴影遮挡、局部阴影遮挡和变化阴影遮挡条件下都拥有良好的性能,具有普适性.

2)所提出的基于ISMA的MPPT控制策略相比于基于P&O的MPPT控制策略在局部阴影遮挡条件下表现更好,可以有效地提高系统发电效率,具有良好追踪精度.

3)所提出的基于ISMA的MPPT控制策略相比于基于SMA和PSO的MPPT控制策略可以大幅缩短系统的追踪时间,具有良好的追踪速度.