带有常数干扰的正则线性系统的镇定
支 霞,冯红银萍
(1.山西警察学院网络安全保卫系,山西太原 030401;2.山西大学数学科学学院,山西太原 030006)
1 引言
由于动态反馈能更充分地利用系统的历史信息,因此可能取得比静态反馈更好的控制效果.动态反馈的优势主要体现在两个方面: 对干扰的鲁棒性和不稳定系统的处理.本文只关注积分控制对常数干扰的鲁棒性.目前有很多处理干扰的控制技术,例如:处理谐波干扰的自适应控制[1-2]、处理一般干扰的高增益技术[3]和估计/消除策略[4-5]以及处理动态已知干扰的内模原理[6]等.
本文将用动态补偿的方法处理常数干扰,由于考虑抽象系统,因此研究具有广泛的一般性.众所周知,PID(proportion integral differential)控制可以消除静态误差,对常数干扰具有鲁棒性.本文受此启发来设计抽象系统的控制器.为了更清楚地说明积分作用对常数干扰的鲁棒性,便于控制器设计,首先,考虑如下二阶系统:
其中:x1,x2是系统状态,u是控制,d∈R是常数干扰.考虑PID控制
其中kp,ki,kd是调节参数.若令
则由系统(1)和反馈(2)组成的闭环系统为
如果我们选择kp,ki,kd使得如下矩阵:
是Hurwitz阵,则由于闭环系统(4)的解满足
则闭环系统(4)变成如下无干扰系统:
由于矩阵(5)是Hurwitz阵,系统(8)的解满足
综合式(7)(9)可得收敛式(6).
受上述例子的启发,本文考虑一般正则线性系统的比例积分反馈镇定器使其对常数干扰具有鲁棒性.本文结构安排如下: 第2节给出基本的预备知识和问题描述;第3节给出本文的主要结果;第4节将抽象结果应用于不稳定热方程;第5节给出数值模拟验证理论结果;最后一节对本文做出总结.
2 问题描述
设X是Hilbert空间,A:D(A)⊂X →X是稠定算子且满足ρ(A)≠∅.通过算子A可以定义两个Hilbert空间: (D(A),‖·‖1)和([D(A∗)]′,‖·‖-1),其中[D(A∗)]′是以X为枢纽空间的D(A)的对偶空间,范数‖·‖1和‖·‖-1分别定义为
由于范数的等价性,Hilbert 空间(D(A),‖·‖1)和([D(A∗)]′,‖·‖-1)不依赖于β ∈ρ(A)的选取.方便起见,在接下来的讨论中,这两个空间分别简记为D(A)和[D(A∗)]′.定义算子如下: 对∀x∈X,y∈D(A∗),
设C ∈L(D(A),R).定义C关于算子A的Λ-延拓为
设A:D(A)⊂X →X是Hilbert空间X上的稠定算子,B ∈L(R,[D(A∗)]′),考虑如下抽象系统:
其中:u是控制,d∈R是常数干扰.本文的目标是设计控制u镇定系统(12).受PID控制(2)的启发,假设控制器u是满足如下形式的动态反馈:
本文将选择函数F和P使得闭环系统(14)的解满足‖x(t)‖X →0,当t→+∞.控制器(14)是PID控 制在一般抽象正则系统的推广,而PID控制在实际应用中有广泛的应用.因此本文对实际应用有一定的指导意义.
方便起见,本文给出如下假设:
假设1设X是Hilbert空 间,A:D(A)⊂X →X是空间X上的稠定算子,B ∈L(R,[D(A∗)]′),C ∈L(D(A),R).假设系统(A,B,C)是正则线性系统,即: 系统(A,B,C)满足如下条件[7]:
i)A在X上生成C0-半群eAt;
ii)B ∈L(R,[D(A∗)]′)和C ∈L(D(A),R)关于eAt允许;
iii)存在s ∈ρ(A)使得(s-)-1BR⊂D(CΛ);
iv)系统的传递函数H(s)=CΛ(s-)-1B在某个右半复平面有界.
3 主要结果
定理1在假设1之下,设系统(A,B)是能稳的,且满足
则对任意的d∈R和x(0)∈X,存在常数ω>0使得系统(14)存在唯一解满足
其中算子P和F可按如下步骤选取:
1)选择K ∈L(D(A),R)指数镇定系统(A,B);
2)令
3)令
证由于系统(A,B)能稳,存在算子K,使A+BK生成X上指数稳定的C0-半群e(A+BK)t.注意到0∈ρ(A+BK),因此(A+BK)-1有意义.
记系统(A,B,C)和(A+BK,B,C)的传递函数分别为H(λ)和HK(λ).由于系统(A,B,C)是正则线性系统,简单计算可知
这说明H(λ)和HK(λ)有相同的零点.由定理假设(15)得
所以,令式(17)-(18)中P和F的定义有意义.
则闭环系统(14)变为
系统(24)可以写成抽象形式
则直接计算可得
由于C0-半群e(A+BK)t指数稳定且L<0,算子AS的分块三角结构意味着AS生成X×R上指数稳定的C0-半群eASt.注意算子相似性(26),算子A也生成X×R上指数稳定的C0-半群eAt.所以式(16)成立.
证毕.
4 不稳定热方程的应用
为了验证定理1中的抽象结果,本节考虑如下不稳定热方程:
其中:u是控制,d是常数干扰.将设计形如式(13)的控制器u来镇定系统(29).该系统的状态空间选为X=L2(0,1).定义
其中δ(·)是Dirac分布.利用算子A和B,系统(29)可以在[D(A∗)]′中写成抽象形式(12).
定义C ∈L(D(A),R)为
由Backstepping方法[8],如下算子K:X →R可以指数镇定系统(A,B): 对任意的f ∈D(A),
其中c1>0是调节参数.简单计算可得
注意到式(17)-(18)以及式(30)-(34),控制器(13)中的算子P和F可选为:对任意的f ∈D(A),
其中L<0 是调节参数.于是动态反馈(13)变为
其中c1>0和L<0是调节参数.由定理1,闭环系统(29)-(37)存在唯一解且满足
其中ω>0是常数.
5 数值仿真
本节将对闭环系统(29)-(37)做数值模拟,用来更直观地验证抽象理论的正确性.本文采用有限差分的离散方法,时间离散步长和空间离散步长分别选为5×10-4和0.05.闭环系统初始状态和干扰选为
控制器调节参数和系统参数选为
系统状态的数值模拟见图1,控制器和干扰的数值模拟见图2.从图1和图2可以看出,控制器有效地补偿了常数干扰,并使得系统状态收敛到零,因此本文的控制器是有效的.
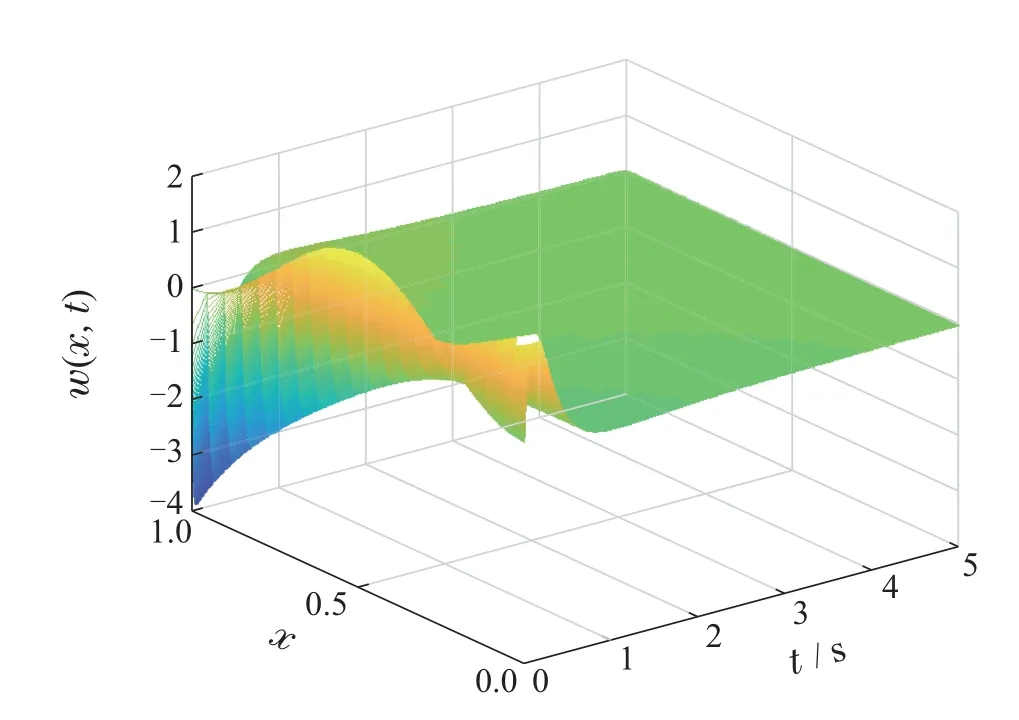
图1 系统状态w(x,t)Fig.1 System state w(x,t)

图2 控制器u(t)Fig.2 Controller u(t)
6 结论
本文研究带有常数干扰的正则线性系统的镇定问题.由于本文关注的是抽象系统,因此研究结果具有广泛的一般性.本文给出的动态反馈规则可以有效地补偿常数干扰并指数镇定系统.抽象结果被成功地应用于带有常数干扰的不稳定热方程的镇定.结果表明,本文的抽方法是非常有效的.

