带边界非线性干扰的反稳定波方程的镇定

梅占东,竺 迪

(西安交通大学数学与统计学院,陕西西安 710049)

1 引言

由于建模的不确定性(如未建模的参数、模型误差)和环境干扰(如风、噪声和温度),在实际工业控制系统中通常会出现不确定性干扰.干扰的存在通常使稳定的边界输出反馈控制器失效,参见文献[1-3].因此,如果出现干扰,重新设计鲁棒稳定控制器是必要的;处理不确定性是现代控制理论中重要的问题之一.处理干扰的控制方法有很多,如内模原理[4-5]、Lyaponov方法[1,3,6]、滑模控制[1,7-9]和自适应控制[10-13],其中,自适应控制方法和内模原理的核心思想是实时估计/抵消.受这种思想的启发,韩京清[14]首先发展了常微分方程的自抗扰控制(active disturbance rejection control,ADRC)方法.由于把干扰当作一个整体、利用扩张状态观测器估计出来、并在反馈环节中抵消掉,ADRC能处理相当一般的干扰,该法几乎不依赖于系统模型.随后,ADRC应用于偏微分方程[1-3,8-9,15-19].在早期偏微分方程(partial differential equation,PDE)自抗扰控制[1,3,8-9,18]中,作者通过引入一些特殊的测试函数把干扰转移到某个常微分方程(ordinary differential equation,ODE)中,从而应用ODE自抗扰控制来处理.这使得扩张状态观测器(extended state observer,ESO)必须采用高增益,并且外部干扰的导数需要有界.为了突破上述限制,文献[16]开发了一种新的具有外部干扰的一维反稳定波动方程的无穷维干扰估计器来代替传统的ODE扩张状态观测器.利用这种方法,他们在文献[5]中考虑具有外部扰动的热方程的输出反馈稳定性.在文献[15-16]激励下,文献[19-20]研究了其他类具有边界控制匹配扰动的波动方程,其中既考虑内部不确定性,也考虑外部扰动.文献[17,21]中作者研究了一类边界力矩控制匹配内部不确定性和外部干扰的一维梁方程.类似的方法也同样适用于具有边界剪切控制且匹配内部不确定性和外部干扰的Euler-Bernoulli 梁方程的指数稳定化[2].受到文献[2,15-17,19-20]的启发,本文考虑边界带控制匹配非线性干扰的一维反稳定波方程的输出反馈指数稳定性,方程描述如下:

其中:w(x,t)是波在位置x和时间t的位移,1≠q>0,u(t)是控制输入,总干扰F(t)=f(w(·,t),wt(·,t))+d(t),f(w(·,t),wt(·,t))是内部不确定性,d(t)是外部干扰,y(t)是输出(测量).对于系统(1)的物理解释,本文参考文献[12].为方便起见,在不引起混淆的情况下,下文中的方程本文省略掉时间和空间变量的域.

在不考虑扰动的情况下(F(t)=0),用Backstepping方法讨论了系统(1)的稳定性,其中全状态是可测量的.在文献[12,22]中,自适应控制方法用于稳定系统,其中q未知.这里必须提到的是,作者通过引入一个额外的传递方程,仅用两个测量值w(0,t)和w(1,t)研究了系统.具体来说,他们引入了以下系统:

其中00,则反馈控制器

指数稳定原始系统,其中c3>0.

然而,文献[16]并没有证明控制器(2)不能抑制干扰,尽管ADRC方法已经被用于处理系统的外部干扰(如果控制器(2)可以抑制干扰,就不需要ADRC).现在本文来澄清这件事情.考虑F(t)≡F时反馈控制器(2)作用下的闭环系统为

在考虑干扰的情况下,文献[6]中结合Lyapunov和Backstepping方法首先研究了系统(1)的稳定性,但是需要完整的状态.如前所述,文献[16]引入一个新的无限维扰动估计器讨论了外部干扰的系统(1)的稳定性.虽然对于F(t)=0的情况,两个测量值足够,但为了处理干扰,他们使用了3个测量值w(0,t),w(1,t),wt(0,t).由于内部不确定性通常出现在工程实践中,文献[20]考虑了既有内部不确定性又有外部干扰的系统;构造了一个无穷维扰动估计器来估计总扰动;他们只使用了两个测量值w(0,t)和w(1,t).文献[20]相比文献[16]的优点是删除了度量值wt(0,t).然而,由于设计了一个额外的观测器来估计原始系统的状态,闭环系统[20,(5.29)和(5.30)]相当复杂: 它由4个波动方程和3个传输方程构成.

在本文中,只考虑两个测量值w(1,t)和wt(0,t))(这继承了文献[20]的优点),并且没有设计额外的观测器(这继承了文献[16]的优点).由于系统关于时间是二阶的,测量值wt(0,t)与文献[16,20]中的w(0,t)区别很大,wt(0,t)不能被视为位移w(0,t)的导数,而w(0,t)不能被认为是wt(0,t)的积分;它们应被视为不同的测量值.事实上,正如文献[11]中所述,几乎所有柔性结构边界控制的结果都是通过测量边界处的速度来实现的.为了设计稳定控制律,核心思想是构造一个无穷维扰动估计器,同时估计状态和总扰动.这与参考文献[2,20]大不相同,后者仅使用估计的总扰动,并设计额外的状态观测器来估计状态;这使本文能够导出一个相对简单的闭环系统(不需要额外的状态观测器).

本文的安排如下: 在第2节中,通过引入了一个辅助系统把总干扰转移到一个指数稳定系统中,然后构造了包括这个辅助系统在内的一个无穷维干扰估计器,用于实时估计状态和总扰动;第3节设计一种基于干扰估计器的输出反馈控制律,并用半群方法证明闭环系统是指数稳定的;在第4节,给出了一些数值模拟.

2 干扰估计器设计

本节的目的是设计一个无限维干扰估计器来估计系统(1)的状态(w(·,t),wt(·,t))和总扰动F(t).由于当F(t)+u(t)=0时的系统(1)是反稳定的,处理干扰并不是那么容易.为了克服这个困难,首先引入一个辅助系统

其中c0,c1>0为调节参数.显然，系统(5)完全由系统(1)的输入和输出决定.令(x,t)=v(x,t)-w(x,t),得

熟知,算子A1生成一个指数稳定C0-半群[23].这表明系统(5)把F(t)转移到了一个指数稳定系统,且不带输入u(t).从而相对于原系统,F(t)更容易处理.

现在对未知输入系统(6)设计如下观测器:

证直接在文献[16]中推论2.1的证明中令c0=0即得结论.证毕.

结合系统(5)和系统(8)得到无穷维干扰估计器

其只依赖于系统(1)的输入和输出.

注1和文献[16]的式(4.4)相似,本文的无穷维干扰估计器只包含两个PDE,而文献[20]的式(5.2)的干扰估计器包含3个PDE.因此本文的干扰估计器比文献[20]简单.

3 输出反馈控制器设计

基于上一节的无穷维干扰估计器,本节的目标是设计系统(1)的输出反馈控制器.受文献[16]的式(3.3)启发,首先引入变量(x,t)=w(x,t)+W(x,t),其中W(x,t)满足

结合式(1)和式(13)得到

本文的输出反馈控制器设计为

其中前两项用于抵消总干扰,剩下的项用于稳定系统(1).对应的闭环系统为

该系统显然是非线性的.

注2和文献[16]的式(5.2)一样,本文的闭环系统(15)只包含3个波方程和1个传输方程,文献[20]的式(5.29)和(5.30)包含4个波方程和3个传输方程.尽管闭环系统(15)和文献[16]的式(5.2)有同的方程个数,本文仅用2个输出量侧,而文献[16]用了3个量测且不包含内部非线性不确定性.这表明本文方法比文献[16,20]更有效更节能.

显然,闭环系统(15)等价于

证由文献[8,23],得到算子B32和B31关于半群eA3t容许.再注意到,将(0,t)和(0,t)视为系统(9)的输出,其观测算子关于半群eA2t容许.由定理1立即得到结论.证毕.

定理3假设(c2-q)/(1-c2)>0,那么对任意满足相容性条件z(1,0)=v(1,0)-w(1,0)的初始条件(w(·,0),wt(·,0),v(·,0),vt(·,0),z(·,0),zt(·,0),W(·,0))∈×H1(0,1),其解(w(·,t),wt(·,t),W(·,t))存在且关于时间t连续.进一步,有

进而得到

定理3表明本文的控制器能够稳定原系统.为了使控制过程有意义,闭环系统(15)还必须有界,下面的定理4就研究这个问题.

ii)对于本文的定理4,不同于开环系统,闭环系统(15)中f(w,wt)的全局Lipschitz条件被去掉了.主要有3方面原因:1)式(17)为线性子系统,且由半群理论可得到((·,t),(·,t))的存在连续性和指数稳定性;2)本文用系统(16)的W部分得((·,t),(·,t))存在连续性和指数稳定性;3)(w(·,t),wt(·,t))的存在连续性和有界性可由原因1)和原因2)得到,于是把f(w(·,t),wt(·,t))+d(t)视为系统(16)的部分的边界非齐次项,得到((·,t),(·,t))的存在唯一性.

4 数值模拟

本节针对闭环系统(15),在MATLAB中采用有限差分方法做一些数值模拟.选择时间和空间步长分别为1/200和1/100.选取非线性内部不确定和外部干扰分别为f(w(·,t),wt(·,t))=sin(w(1,t))和d(t)=sin(2t).参数和初值选取q=0.5,c0=c1=1,c2=0.8,w(x,0)=x2-2x,wt(x,0)=0,z(x,0)=x3,zt(x,0)=0,v(x,0)=vt(x,0)=0,W(x,0)=2x.

图1-4 分别表示闭环系统(15)的状态w(x,t),W(x,t),v(x,t)和z(x,t).数值结果显示,闭环系统的状态w(x,t)和W(x,t)随时间的增加迅速衰减,这展示了定理3的有效性;状态v(x,t)和z(x,t)始终保持有界,这表明了定理4的正确性.

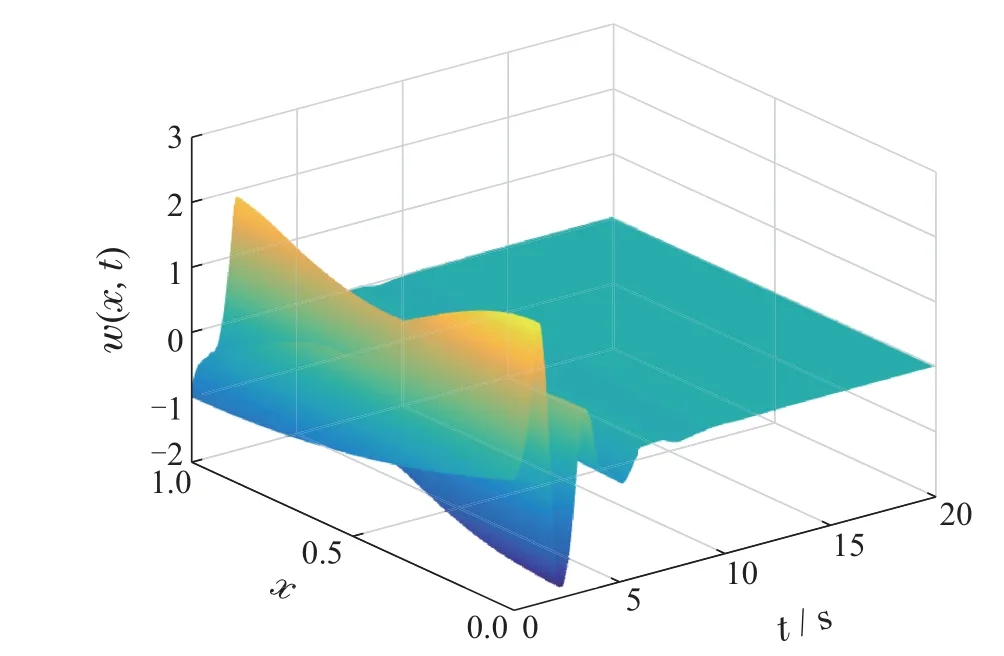
图1 状态w(x,t)Fig.1 The state of w(x,t)

图2 状态W(x,t)Fig.2 The state of W(x,t)

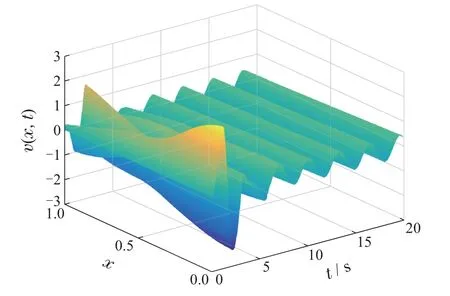
图3 状态v(x,t)Fig.3 The state of v(x,t)

图4 状态z(x,t)Fig.4 The state of z(x,t)