复合材料负泊松比结构等效弹性力学理论建模

赵昌方,GOH Kheng Lim, 乐贵高, 任 杰, 仲健林*

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.纽卡斯尔研究与创新研究所(NewRIIS),新加坡 609607;3.英国纽卡斯尔大学 科学、农业和工程学院,泰恩河畔纽卡斯尔 NE1 7RU)

碳纤维增强复合材料(CFRP)因具有优异的力学性能而被广泛用作工程结构的成型材料[1-4]。负泊松比结构(NPRS)是一类具有超力学性能的新型结构[5-7],也被称为拉胀结构(auxetic structure),具有异于常规材料的抗压痕性。许多学者将CFRP与NPRS进行结合,形成复合材料轻量化超力学抗冲击结构,试图获得更高的缓冲吸能收益。负泊松比效应或拉胀效应需要通过内凹结构或扭转结构来实现,属于一类异型构件,不容易成型。许多研究均基于增材制造技术来设计CFRP负泊松比结构[8-9],但这将会增加造价、降低结构性能和限制结构尺寸[10-12]。为此,赵昌方等[7,13-15]基于传统的高温热压成型法,采用单层单向预浸料按照0°/90°的铺层方式,制备了具有层合板截面属性的内凹六边形负泊松比结构(re-entrant NPRS),并开展了一系列实验研究。然而,这些研究主要通过实验和有限元分析开展,理论预测模型尚未得到解决。

关于负泊松比结构的等效力学理论建模研究较多,但大多结构的胞壁为各向同性材料,结构的变形容易把握,建模方法相对容易。文献[5-6,16]基于欧拉梁理论,针对各向同性材料制备的内凹六边形和星形负泊松比结构进行了二维等效弹性力学建模,并通过有限元分析讨论了模型的有效性。NIRANJAN 等[17]采用3D 打印制备了丙烯腈-丁二烯-苯乙烯材料的负泊松比结构,并通过弯曲挠度建立了结构的等效弹性模量理论公式。QUAN 等[18]采用3D 打印制备了凯夫拉纤维增强聚乳酸材料的负泊松比结构,并基于弯曲梁理论计算了胞壁变形,进而获得了等效弹性模量和泊松比理论模型。JIANG等[19]通过增材制造方式制备了聚乳酸基负泊松比结构,并基于各位置的几何变形给出了结构的泊松比计算经验公式。韩广等[20]设计了铝制新型斜十字负泊松比结构,并根据能量法和卡氏第二定理建立了等效弹性模量、等效泊松比解析表达式。吴秉鸿等[21]基于弹性力学原理,给出了钢制星型负泊松比结构的等效泊松比和等效弹性模量解析表达式。

为了进一步丰富和拓展CFRP-NPRS的研究内容,需建立等效弹性力学理论模型,揭示负泊松比结构的负泊松比效应实现机理和力学行为。本研究结合欧拉梁理论和材料力学相关知识,建立了负泊松比结构的等效弹性模量和等效泊松比理论模型,通过关联结构的几何尺寸获取了等效泊松比及弹性模量的曲面响应,并通过实验和仿真讨论了模型的适用性。

1 等效弹性力学建模

1.1 负泊松比效应实现

负泊松比结构通常源自于负泊松比材料的微观形貌,例如多孔泡沫、黄铁矿晶体等等。材料实现负泊松比效应的机理是:受拉时,材料微观孔壁横向向外传递载荷,致使材料横向膨胀形成拉伸-膨胀的变形特征;受压时,材料微观孔壁则横向向内传递载荷,致使材料横向收缩形成压缩-收缩胀的变形特征。不难发现,负泊松比效应的实现机理在于材料内部的微观结构,对于没有微观特征的均质材料,例如常见的钢、铝、塑料等,很难呈现负泊松比效应。将材料的微观特征放大制成结构,结构的变形仍保持着原先的受力变形特性,从而出现了负泊松比结构。

常见的双箭头结构是负泊松比结构的经典构型,如一对箭头构成的内凹六边形结构、4个箭头的星形结构及其组合/变型结构等。二维内凹六边形的线条简化结构如图1所示,当箭头帽受拉后,会将2个箭头帽组成的“内凹V 形”拉直(V 形夹角/内凹角α增大),使得箭头杆向外横向运动,从而实现拉胀现象,即拉胀效应;同理,当箭头帽受压后,“内凹V 形”会收缩(V 形夹角/内凹角α减小),使得箭头杆向内横向运动,从而实现压缩-收缩现象,即负泊松比效应。可以看出,负泊松比结构的负泊松比效应通过其胞壁变形实现,且受一对力偶作用的弯曲变形占据主导地位。其中,定义面内的内凹方向为x方向(1#方向)、垂直于内凹方向为y方向(2#)方向,垂直于平面外的方向则为z方向(3#方向)。

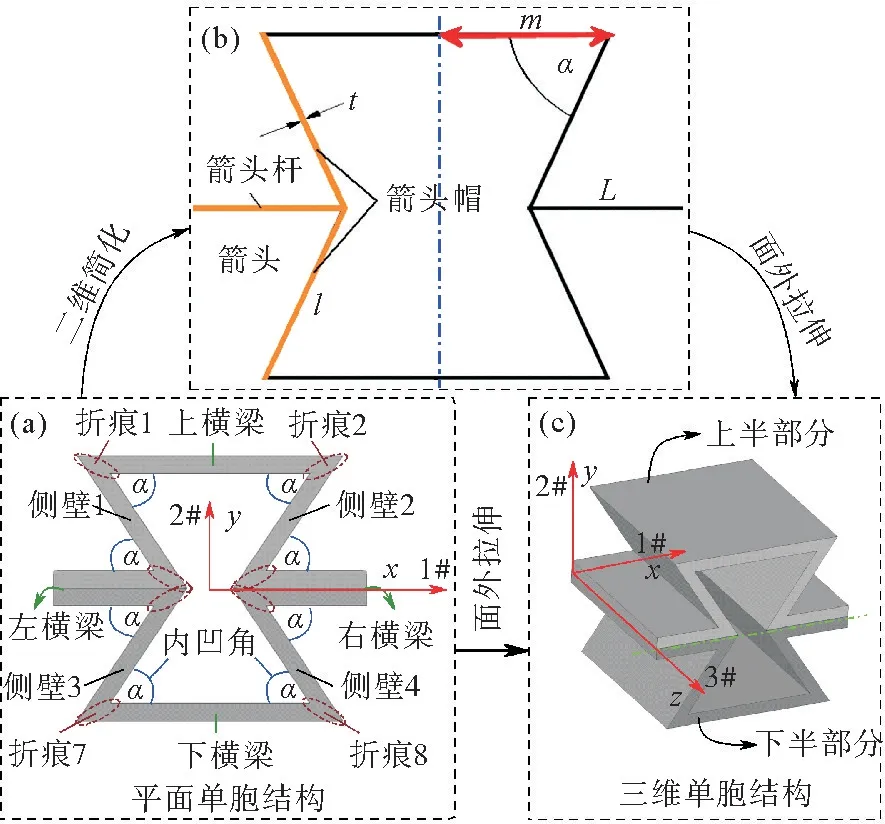
图1 CFRP内凹负泊松比结构跨维度演化及部件命名Fig.1 Cross-dimensional evolution and component naming of CFRP concave negative Poisson′s ratio structure

1.2 等效弹性力学建模基本假设

CFRP层合板由多个具有方向性的单层构成,使得层合板具有明显的各向异性,造成了CFRP 负泊松比结构等效弹性力学建模的困难。为便于分析,需弱化CFRP 的各向异性特征,故作出以下假设:

1)CFRP层合板可视为正交均质材料;

2)层合板的各单层材料等厚,是正交各向异性材料,具有线弹性力学行为;

3)CFRP层合板的变形增量满足弹性小变形假设,且面内弹性拉/压小变形可以忽略,仅考虑弯曲变形;

4)弹性弯曲变形过程中CFRP 层合板未发生任何失效,例如分层破坏、层间开裂等;

5)满足变形一致性假设,即层合板各层之间为粘接,各层变形一致,没有层间相对变形,且中性面应变为零;

6)满足直法线不变假设,即变形前垂直于层合板中性面的横向法线在变形后也与中性面垂直,且长度不变;该假设说明面外剪切应变为零,即γxz=γyz=0,εzz=0;

7)面外z方向的应力与面内x和y方向相比很小,可以忽略,即σzz=0;

8)满足平面应力假设,即各单层板均处于平面应力状态,且不考虑体积力的影响;

9)CFRP层合板的厚度与其长度和宽度相比很小,属于薄板结构;

10)CFRP负泊松比多胞结构等效力学可由其单胞结构进行表征。

经典层合板理论在Kirchhoff-Love平板理论假设下成立,Kirchhoff假设等价于上述假设5)、6)、7)。分析二维平面结构变形用的Euler-Bernoulli梁理论的前提假设是不考虑梁横向的剪切应变,即上述假设中的6)和7)。考虑梁的横向剪切应变时,需采用Timoshenko梁理论;若是板结构,则需采用一阶剪切变形层合板理论。由图1可知,研究对象(三维内凹负泊松比结构)是二维构型的面外拉伸,其面内方向(1#和2#方向)受载的力学行为具有二维特征。因此,在不考虑面外剪切时可采用Euler梁理论来建立等效弹性力学模型,推导等效弹性模量和等效泊松比。

1.3 1#方向压缩等效弹性力学模型

假设结构的拉伸和压缩具有相同的等效弹性力学行为,若以压缩加载为例,结合实验结果[13-14],可得1#方向的受力图示,如图2。其中,p为载外荷,t为厚度,l为侧壁长度,α为内凹角,L为左、右连接梁(对于周期性胞结构的代表性体积单元,有m=L);另设H为2#方向高度,W为1#方向宽度,Z为3#方向厚度;结构各部件的命名方法参考图1。

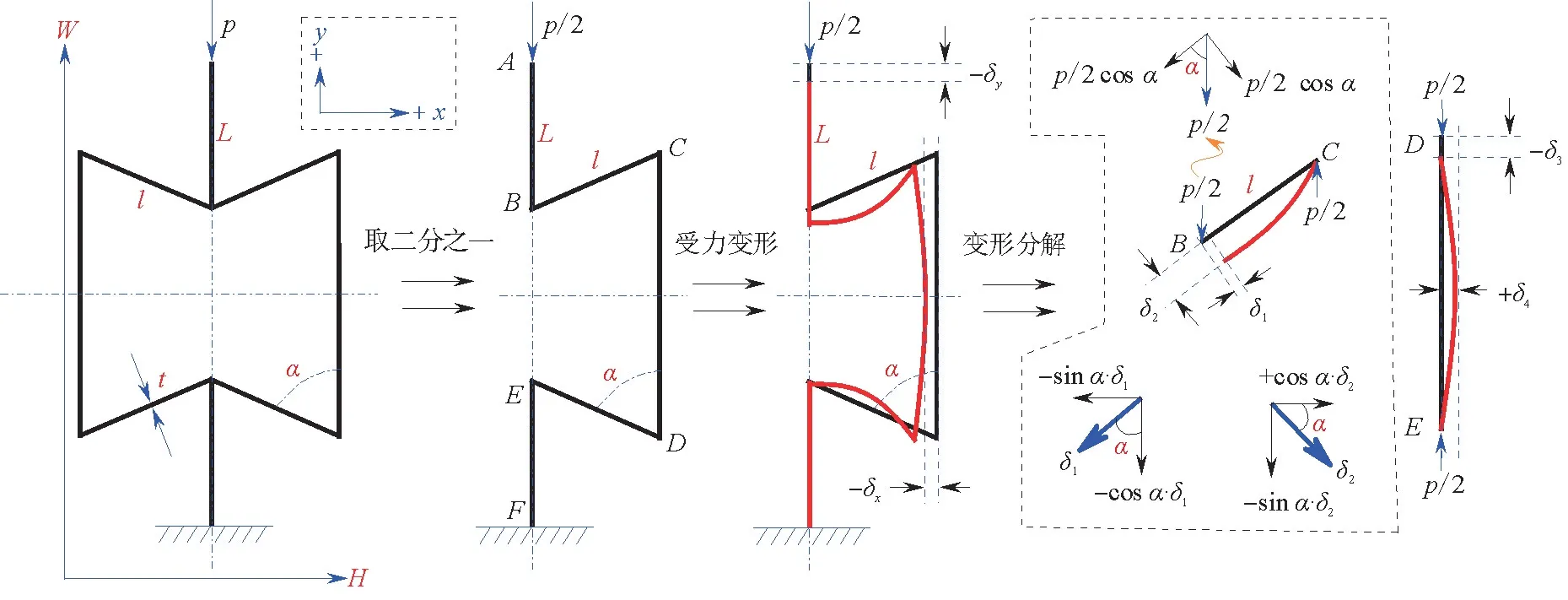
图2 CFRP负泊松比结构1#方向压缩变形图示Fig.2 Compression deformation in 1#direction of CFRP negative Poisson′s ratio structure

根据几何关系有,结构高度H和结构宽度W依次为

理想情况下胞结构发生对称变形,则此处取一半为分析对象,有等效应力为

式(3)中,F1和A1分别为名义载荷和横截面积。

沿1#方向压缩时,CFRP 层合板左、右横梁(A-B、E-F)发生受压变形,侧壁(B-C,D-E)发生弯曲变形,上、下横梁(C-D)也发生弯曲变形。由于CFRP层合板的面内刚度大,横梁的面内压缩变形远小于侧壁的弯曲变形,故忽略压缩变形。根据Euler梁理论和材料力学[5-6,16],将侧壁l视为均质悬臂梁弯曲受载进行求解,得变形结果为

式(4)和式(5)中,δi表示位移量,E0为层合板材料的弹性模量,Iz为截面惯性矩。

将上、下横梁视为两端受压的屈曲压杆,服从弹性Euler屈曲力学状态。认为压力超过Euler临界力后的塑性行为是失效或破坏,不予以考虑,则Euler临界压力为

式(6)中,A为压杆横截面积,λ为长细比。

然而,压杆的屈曲变形计算较为复杂,需多次积分[6],难以实现定量分析。为便于计算,可将屈曲变形简化为纯弯曲变形。同理,根据Euler梁理论及材料力学理论,可得到上、下横梁的弹性变形为

然而,梁B-C和D-E的另一端与压杆C-D相连,使得变形发生耦合。梁B-C和D-E在x方向的变形相等,虽然在弯曲端是正向位移,但在自由端却是收缩位移,理应为负向,即δ2的横向分量在整体上表现为负。从而,可得二分之一结构横向和纵向的变形总量,即

根据名义应变的定义,可得二分之一结构的等效应变为

根据泊松比概念及其定义[5],可得CFRP 负泊松比结构的等效泊松比,即

根据广义胡克定律(σ=Eε)可得,等效弹性模量为

上述方程得出的E1和v1即是CFRP负泊松比结构1#方向加载的等效弹性模量和等效泊松比。

1.4 2#方向压缩等效弹性力学模型

在理想情况下,沿2#方向压缩时,胞结构发生对称变形。由于结构高度对称,此处取四分之一为分析对象,有等效应力为

式(14)中,F2和A2分别为名义载荷和横截面积。

由于压缩时上、下横梁及左、右横梁均不发生变形,仅是发生平移,故不考虑其形变。因此,压缩变形主要由侧壁l贡献,侧壁发生弯曲变形,如图3所示。同理,基于Euler梁理论和材料力学弯曲理论,可得变形量分别为

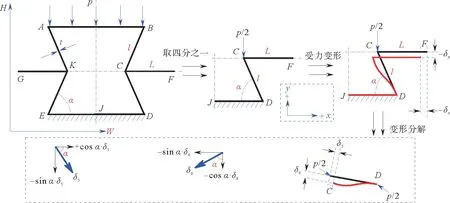
图3 CFRP负泊松比结构2#方向压缩变形图示Fig.3 Compression deformation in 2#direction of CFRP negative Poisson′s ratio structure

因此,四分之一结构的横向和纵向变形总量分别为

结合横、纵方向的长度,可得x、y方向的名义应变为

从而,根据泊松比的定义可得2#方向压缩时的等效泊松比

同理,可得2#方向压缩的等效弹性模量,即

2 等效弹性力学几何参数影响规律

2.1 材料参数及边界条件

针对制备的实际模型[14-15],其结构的尺寸参数分别为t=2 mm、l=17.3 mm、L=11.5 mm、Z=32 mm、α=60°(m=L)。层合板的铺层规则为[0°/90°]10,结构面内方向下层合板胞壁的剪切模量G和弹性模量E0可通过经典层合板理论[22]进行计算。

在进行参数分析时,需保证结构的合理性,即保证所取参数下结构仍然是内凹六边形结构。尺寸关系包括壁厚t、侧壁长度l、横梁半长L、内凹角α等4个,4个参数互相耦合,因此需先确定2个不变量,才能讨论其它参数的变化范围。壁厚t一方面要保证结构为薄壁结构,一方面可以持续增大直到两箭头互相接触,1/4 结构壁厚关系如图4(a)所示。此外,保证胞壁结构的条件为壁厚远小于侧壁长度l和横梁半长L。为此,壁厚t的尺寸约束条件为

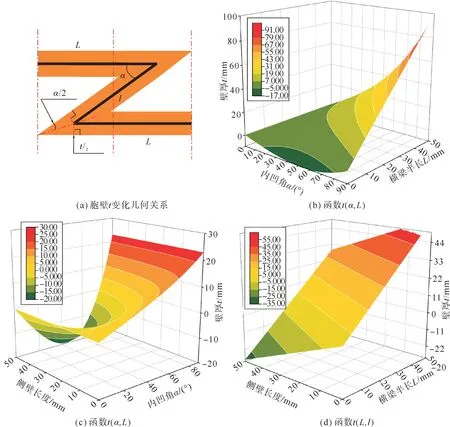
图4 胞壁相关性分析Fig.4 Correlation analysis of cell walls

横梁半长L是影响胞壁变化的主要关系,而α次之。随着L的增大,内部空间横向增大,胞壁t得以增大,如图4(b)。内凹角α的增大,使得内部空间成倍扩大增大,则胞壁t持续增大,如图4(c)。在正值区间内,随着l的增大却导致胞壁t减小,如图4(d)。当响应面的边界很大时,需选取一定的范围进行显示,从而会出现截断的情况,类似于图4(d)中L接近50 mm 时曲面截断的现象,下文中也会有类似情况。在实际设计中,需考虑胞壁厚度与边长的关系,即时刻保持结构为薄壁结构状态,从而满足上述的基本假设。

胞的内凹角由结构的宽度W、横梁半长L和侧壁长度l决定,是个关联性极强的衍生参数。负泊松比结构内凹角α的理论取值区间为(0°,90°),内凹角α大于90°则为外凸六边形结构,内凹角α小于0°则结构发生干涉。然而,不同因变量条件下内凹角α的取值区间不尽不同,应分别讨论。由于变量多余3个,需确定1个再讨论另外2个。在保证薄壁结构的前提下,胞壁t的变化范围较小,对内凹角的影响较小,故可以作为一个不变量,以降低复杂程度。如图5(a),当胞壁t不变,侧壁长度l不变时,内凹角α在横梁半长L的变化下而变化,横梁绕着直径为侧壁长度的圆转动。在保证内凹结构的条件下,有2个极限位置,即横梁与侧壁垂直时、横梁与侧壁共线时,这2个极限位置使得内凹角α的取值区间为

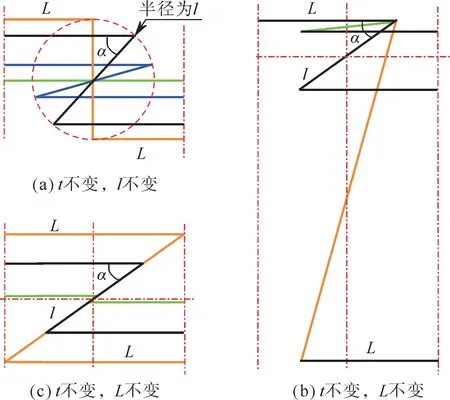
图5 内凹六边形结构几何变化关系Fig.5 Geometric changes of concave hexagon structure

同理,当胞壁t不变,横梁半长L不变时,内凹角α在侧壁长度l的变化下而变化。对应的2个极限位置分别是,横梁与侧壁共线、侧壁长度无限大,如图5(b)。因此,内凹角α的取值区间为

当胞壁t不变,内凹角α不变时,横梁半长L与侧壁长度l一起发生等比例变化。对应的2个极限位置分别是,横梁与侧壁共线、侧壁在横梁方向上的投影与横梁等长,如图5(c)。从而,横梁半长L和侧壁长度l的取值关系为

对于一个给定尺寸的结构,内凹角为最小极限值0°时,表明结构被挤压,内部没有空间,各胞壁互相平行。内凹角处于最大极限值90°时,结构转化为矩形,不具有负泊松比效应。内凹角大于90°后,结构转变成外凸的六边形结构,不再属于内凹负泊松比结构的范畴。接下来将进行的影响因素曲面响应分析中,内凹角的合理取值范围应满足上述3个不等式,以保证结构的合理性。

2.2 1#方向压缩尺寸参数影响规律

基于上述推导的等效弹性力学模型,通过数值计算,可得等效弹性模量、等效泊松比与内凹六边形负泊松比结构几何尺寸的关系。由于内凹六边形结构尺寸具有耦合关系,进行耦合因素三维曲面响应分析更为合理。因此,当考虑壁厚t、侧壁长度l与等效泊松比v1的关系v1(t,l)时,确定横梁半长L=11.5 mm,内凹角α=60°;考虑壁厚t、横梁半长L与等效泊松比v1的关系v1(t,L)时,确定侧壁长度l=17.3 mm,内凹角α=60°;考虑横梁半长L、侧壁长度l与等效泊松比v1的关系v1(l,L)时,确定壁厚t=2 mm,内凹角α=60°;考虑壁厚t、内凹角α与等效泊松比v1的关系v1(t,α)时,确定侧壁长度l=17.3 mm,横梁半长L=11.5 mm。基于此控制变量法绘制的曲面响应关系见图6。

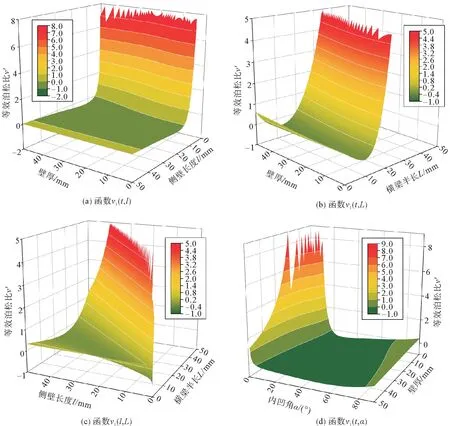
图6 等效泊松比-尺寸参数响应面Fig.6 Parameter response surfaces of equivalent Poisson′s ratio-size

v1(t,l)曲面响应中,负泊松比效应在一定范围内得以实现;但随着侧壁长度l和壁厚t的增加,泊松比逐渐增大到0,图6(a)。v1(t,L)曲面响应中,横梁半长L介于5 mm 到20 mm 时具有负泊松比效应,且随着壁厚t增大泊松比略有增加,图6(b)。v1(l,L)曲面响应中,负泊松比效应也被实现了,图6(c);侧壁长l等于横梁半长L的一半位置时,内凹结构退化为封闭三角形结构,此时结构两箭头接触,横向变形为零,故泊松比逐渐增大为零。v1(t,α)曲面响应中,内凹角α介于10°到80°之间时,实现了负泊松比效应;低于10°时结构内部空间趋于零,泊松比趋于无穷大,图6(d)。值得注意的是,观察图6(a)～(d)可知,壁厚t对泊松比的影响并不大,可以认为壁厚t为一个常数。

将壁厚t设为定值2 mm 后,同样,基于三维曲面响应分析尺寸参数对等效弹性模量的影响。在(E1/E0)(α,L)函数关系中,t=2 mm,l=17.3 mm;在(E1/E0)(α,l)函数关系中,t=2 mm,L=11.5 mm;在(E1/E0)(l,L)函数关系中,t=2 mm,α=60°;在(E1/E0)(α,t)函数关系中,l=17.3 mm,L=11.5 mm。通过数值软件进行绘制,等效弹性模量受尺寸参数影响结果见图7。

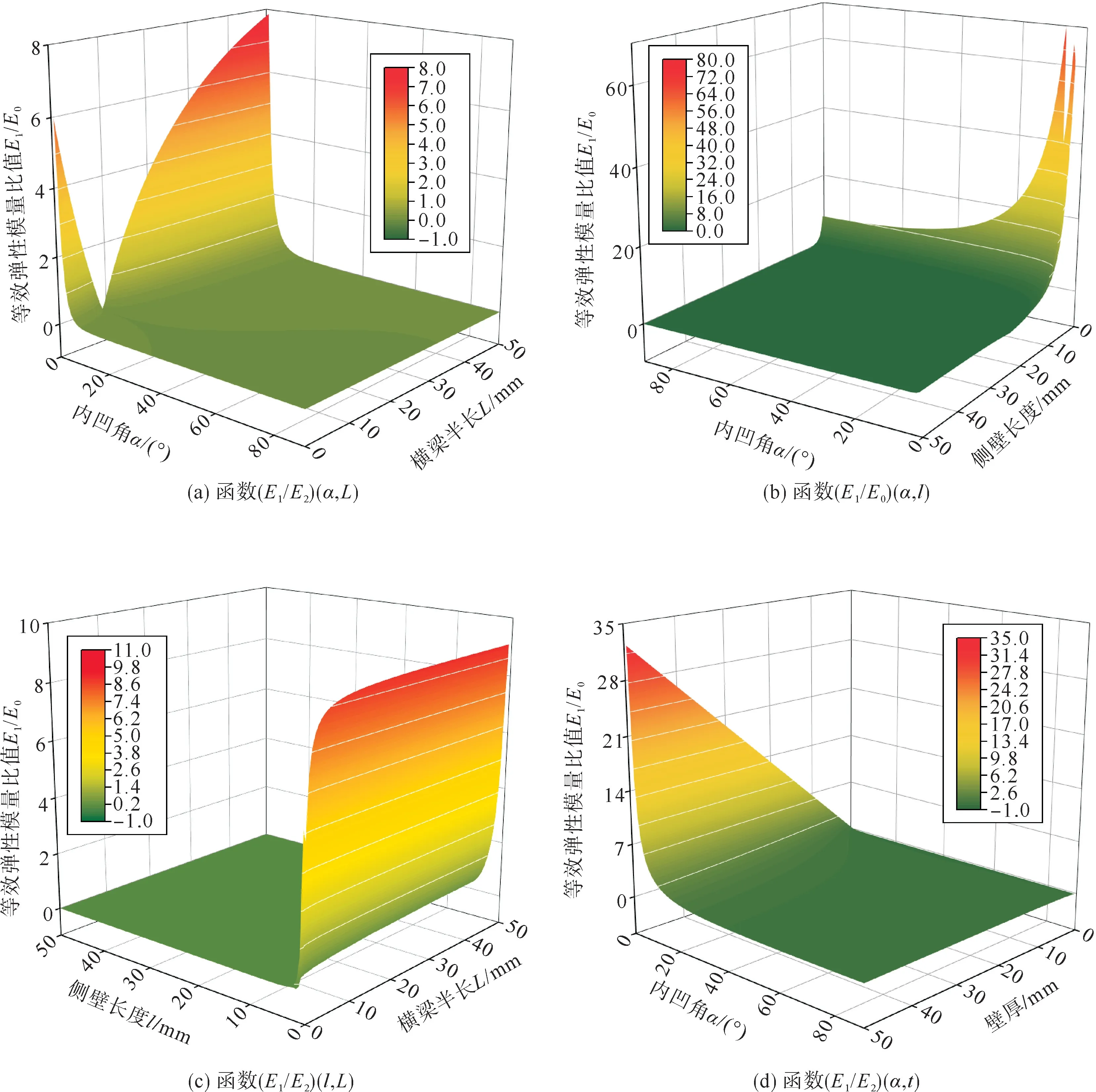
图7 等效弹性模量比值-尺寸参数响应面Fig.7 Parameter response surfaces of equivalent elastic modulus ratio

(E1/E0)(α,L)曲面响应显示,内凹角α越小,等效弹性模量比值E1/E0越大,而基材模量E0是定值,故等效弹性模量E1越大,如图7(a)所示,这是合理的结果;因为内凹角减小,则结构的内部空间减小,趋于零时结构退化为一个密实体,此时弹性模量快速增大。(E1/E0)(α,l)曲面响应显示,内凹角α和侧壁长度l减小能使等效弹性模量E1增大,如图7(b)所示,这也是结构密实化带来的理论结果。(E1/E0)(l,L)曲面响应显示,胞元侧壁l越短,等效弹性模量E1越大,而横梁半长L影响较小,如图7(c)所示,这也是合理的现象;1#方向压缩时,上、下横梁主要发生屈曲,而侧壁发生弯曲,是影响结构等效弹性力学的主要因素;侧壁l减小,则结构也趋于密实,所以等效弹性模量E1会增大。(E1/E0)(α,t)曲面响应显示,内凹角α越小,壁厚t越大,则等效弹性模量E1越大,如图7(d)所示,这也是密实化带来的结果;内凹角减小,壁厚增大,则内部空间减小,结构趋于一个密实体,等效弹性模量较空心结构大。

2.3 2#方向压缩尺寸参数影响规律

2#方向压缩时,同理,需确定两个不变量,然后进行曲面响应分析。当考虑内凹角α、侧壁长度l与等效泊松比v2的关系v2(α,l)时,确定横梁半长L=11.5 mm,壁厚t=2 mm;考虑内凹角α、横梁半长L与等效泊松比v2的关系v2(α,L)时,确定侧壁长度l=17.3 mm,壁厚t=2 mm;考虑侧壁长度、l横梁半长L与等效泊松比v2的关系v2(l,L)时,确定壁厚t=2 mm,内凹角α=60°;考虑内凹角α、壁厚t与等效泊松比v2的关系v2(α,t)时,确定侧壁长度l=17.3 mm,横梁半长L=11.5 mm。基于此,绘制的曲面响应关系见图8。

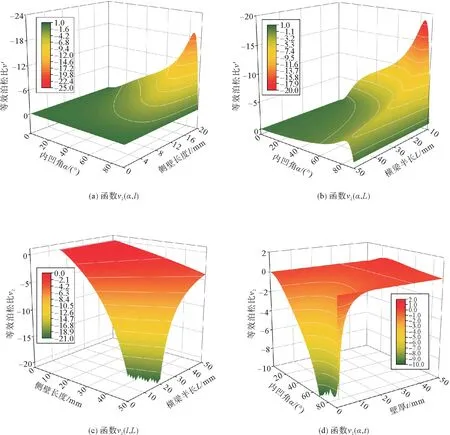
图8 等效泊松比-尺寸参数响应面Fig.8 Parameter response surfaces of equivalent Poisson′s ratio-size

从v2(α,l)的曲面响应图可知,随着内凹角α增大、侧壁长度l增大,则负泊松比v2越大,如图8(a)所示;这是因为内凹角增大和侧壁增长都会使得压缩时横向应变增大,从而增大负泊松比效应;然而,内凹角区域90°时,泊松比趋于0,因为结构已不再属于负泊松比结构。从v2(α,L)的曲面响应可知,随着内凹角α增大其负泊松比v2先增大后减小,随着横梁半长L增大其负泊松比v2逐渐减小,因为结构“长大”了,具有更多的可变形胞壁,如图8(b)所示。v2(l,L)的曲面响应图可知,横梁半长L减小、侧壁长度l增大,负泊松比值v2增大,如图8(c)所示;同理,侧壁l增长结构也有“长大”的趋势。v2(α,t)的曲面响应图可知,内凹角α增大、壁厚t减小,负泊松比值v2增大,如图8(d)所示;壁厚t减小则更容易发生变形,内凹角α增大结构会“长大”。

同理,在(E2/E0)(α,l)函数关系中,t=2 mm,L=11.5 mm;在(E2/E0)(α,L)函数关系中,t=2 mm,l=17.3 mm;在(E2/E0)(l,L)函数关系中,t=2 mm,α=60°;在(E2/E0)(α,t)函数关系中,l=17.3 mm,L=11.5 mm。绘制的参数影响下2#方向压缩等效弹性模量比值E2/E0三维响应面如图9所示。

图9 等效弹性模量比值-尺寸参数响应面Fig.9 Parameter response surfaces of equivalent elastic modulus ratio

(E2/E0)(α,l)曲面响应中存在一个奇异区域,该区域内等效弹性模量趋于无穷,如图9(a),这是2L-l·cosα=0导致的,可以忽略其存在;为此,随着内凹角α的增大、侧壁长度l的减小,等效弹性模量比值E2/E0增大,但比值小于1;侧壁l减小会导致结构密实化,等效弹性模量E2会增大,但仍然小于基材模量E0,这是2#方向压缩的结果;因为该方向压缩的力学性能仅由侧壁弯曲贡献,而材料的弯曲模量总小于其拉、压模量,故等效弹性模量E2不可能超越基材模量E0。(E2/E0)(α,L)曲面响应显示,内凹角α增大、横梁半长L减小,等效弹性模量E2增大,如图9(b)所示,这也是胞壁长度减小导致结构致密实化的结果。(E2/E0)(l,L)曲面响应中,在2L-l·cosα=0附近也存在不连续现象,如图9(c)所示,此时等效弹性模量计算公式分母为零,故结果趋于无穷大;但随着侧壁长度l减小,等效弹性模量E2增大,这是密实化带来的结果。(E2/E0)(α,t)曲面响应显示,随着壁厚t的增大,等效弹性模量E2增大,同时内凹角α在40°左右时有最大值,如图9(d)所示,这也是结构致密化导致的结果;值得注意的是,此时等效弹性模量比值大于1,因为壁厚增大会导致结构趋于密实体,增强结构的刚度/模量。

总的来说,不论是1#还是2#方向加载,负泊松比结构的4 个尺寸参数(L、l、t、α)对等效泊松比和等效弹性模量都有明显的影响。假设使等效泊松比或弹性模量出现最大值变化的几何参数值为几何特征值,则可将影响规律总纳为:在特征值附近,壁厚t增大导致等效泊松比增大并趋于零、等效弹性模量增大,侧壁l增大致使等效泊松比增大、等效弹性模量降低,横梁半长L增大导致等效泊松比增大、等效弹性模量变化不大,内凹角α增大对等效泊松比和等效弹性模量的影响并未形成统一规律。

3 等效弹性力学理论模型评估

CFRP负泊松比结构通过设计组合式模具进行制备,每次制备一半,然后对称粘接制备完整的负泊松比结构,详细的制备工艺可参考之前的工作[13-14]。在前期开展的准静态压缩实验中,通过三维全场应变测试和分析系统获取了CFRP 负泊松比结构的泊松比,并获取了结构的压缩失效过程和力学响应[13];开展的有限元分析也预测了结构的泊松比变化规律[14]。

为验证理论-实验-模拟方法获取结构等效弹性力学的一致性,进行了理论模型的评估分析。基于理论解析模型,代入相应的尺寸参数后计算得出:v1约为-0.335,v2约为-6.931。如图10所示,将实验和模拟得到的泊松比与理论范围进行对比可知:1#方向压缩时,实验值和模拟值均落在理论预测区间内,模拟值后半段溢出理论区间是因为结构发生了失效而不再处于弹性状态;2#方向压缩时,实验值与模拟值因失效模式的差异而存在出入,说明有限元模型需要改进,理论预测区间因考虑层合板的弯曲变形而具有较大误差。1#方向压缩时,理论值对实验值的最大误差约为-0.442 5,理论值对模拟值的最大误差约为-0.621 7;2#方向压缩时,理论值对实验值的最大误差约为-6.306 2,理论值对模拟值的最大误差约为-5.531 0。由此可知,采用弯曲小变形的Euler梁方法来建立CFRP层合板负泊松比结构等效弹性力学还不够妥当,未来可采用经典层合板力学、考虑分层滑移/局部拉压失效/纤维层微弯曲等因素进行建模。

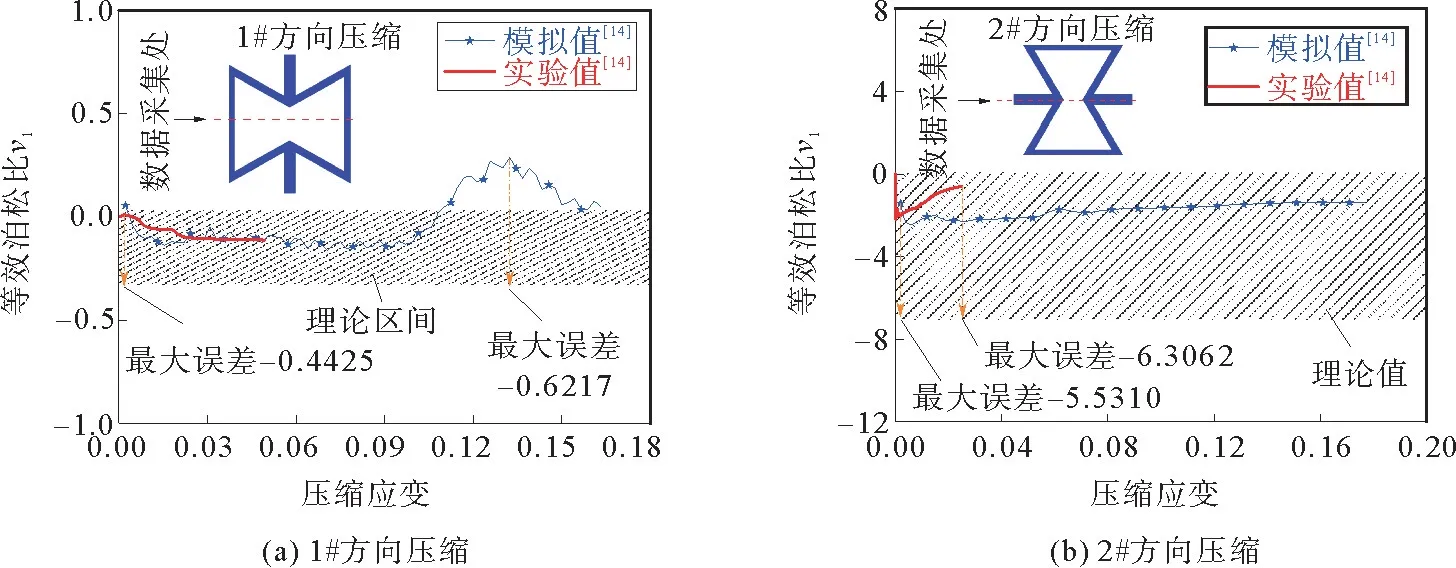
图10 理论-实验-模拟的负泊松比值评估Fig.10 Negative Poisson′s ratio value evaluation for theory,experiment and simulation

4 结 语

碳纤维增强复合材料(CFRP)负泊松比结构能实现先进材料优势和超力学结构特征的叠加,是缓冲吸能领域中颇具发展潜力的结构,从而深入开展其力学相关的研究具有重要意义。针对未开展的等效弹性力学理论模型基于Euler梁理论进行了尝试性探索,主要研究内容如下:

1)揭示了内凹六边形负泊松比结构实现拉胀效应或负泊松比效应的机理;

2)推导了CFRP在1#和2#两个面内方向的等效泊松比和等效弹性模量理论模型;

3)采用控制变量法对等效泊松比和等效弹性模量进行了尺寸参数的影响规律研究;

4)获取了解析解的理论范围,并与实验值和模拟值对比,分析了理论模型的预测效果。

结果表明,采用Euler梁理论建立的等效弹性力学理论模型预测区间虽能囊括实验和模拟结果,但存在较大误差,这是将CFRP 层合板考虑成均质材料造成的问题。在后续的研究中,或许可以通过经典层合板理论矩阵法计算负泊松比结构胞壁的弯曲变形,再计算等效弹性力学常数,提高理论模型的预测精度。