图解与双曲线有关的区域问题*

江苏省张家港市外国语学校 (215600) 何 威 魏 丹

一、问题提出

圆是完美的图形,学生容易理解圆的有关区域问题,如圆分整个平面为三个部分:圆上、圆内、圆外;再如从平面内一点P做圆的切线的情况:当P在圆内时,0条;当P在圆上时,1条;当P在圆外时,2条.这一结论可类比推理,在椭圆、抛物线中得到十分类似的结论.然而到了双曲线,情况就复杂多了,这一部分是学生理解和识记的难点.相比于圆与椭圆,双曲线的图象一方面是由分开的左、右支构成的,另一方面双曲线有渐近线,这些特性使得需要分类讨论的情况更多.

为了帮助学生厘清与双曲线有关的区域问题,笔者在教学中用图解的方式,让学生从形感知,从数推理,在知识之间构建整体的联系,借助直观化策略提升学生的推理与想象能力,加深对双曲线区域问题的理解与记忆.

二、图解区域问题

2.1 双曲线分平面的不同区域

类比点与椭圆的位置关系,点与双曲线的位置关系如何刻画?

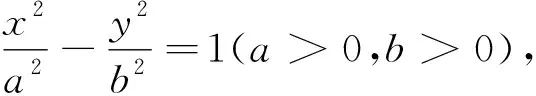
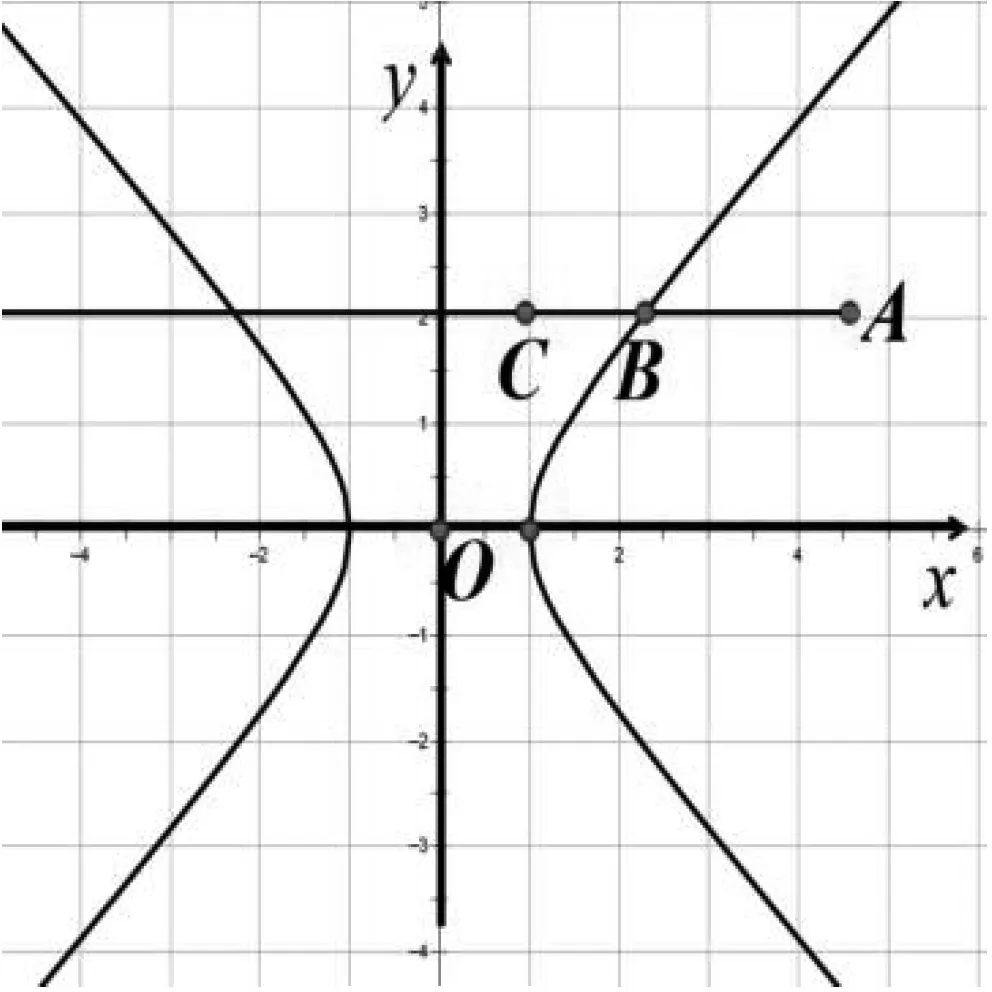
图1

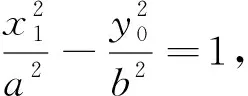
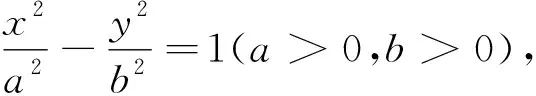
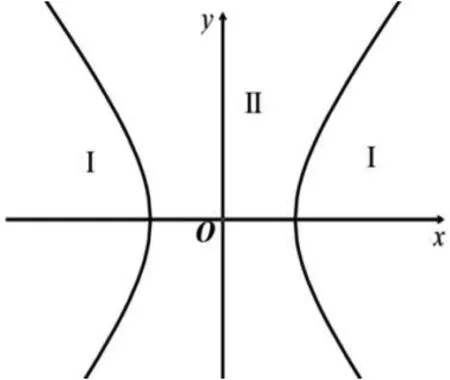
图2

实际上,区域Ⅰ称之为双曲线的内部,区域Ⅱ称之为双曲线的外部.

2.2 双曲线中点弦存在的区域

问题2 中点弦是圆锥曲线中的重要性质,双曲线的中点弦什么时候存在?

二是用层级式的学习，用与优秀人员之间的差距，让阿姨从急功近利式的节奏中慢下来，帮助她们认真充电，做好储备。

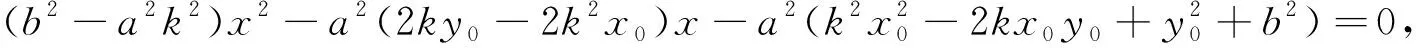
结论2 (如图3)①若点P在双曲线上,或渐近线上,或在区域Ⅲ时,Δ≤0,此时中点弦不存在.

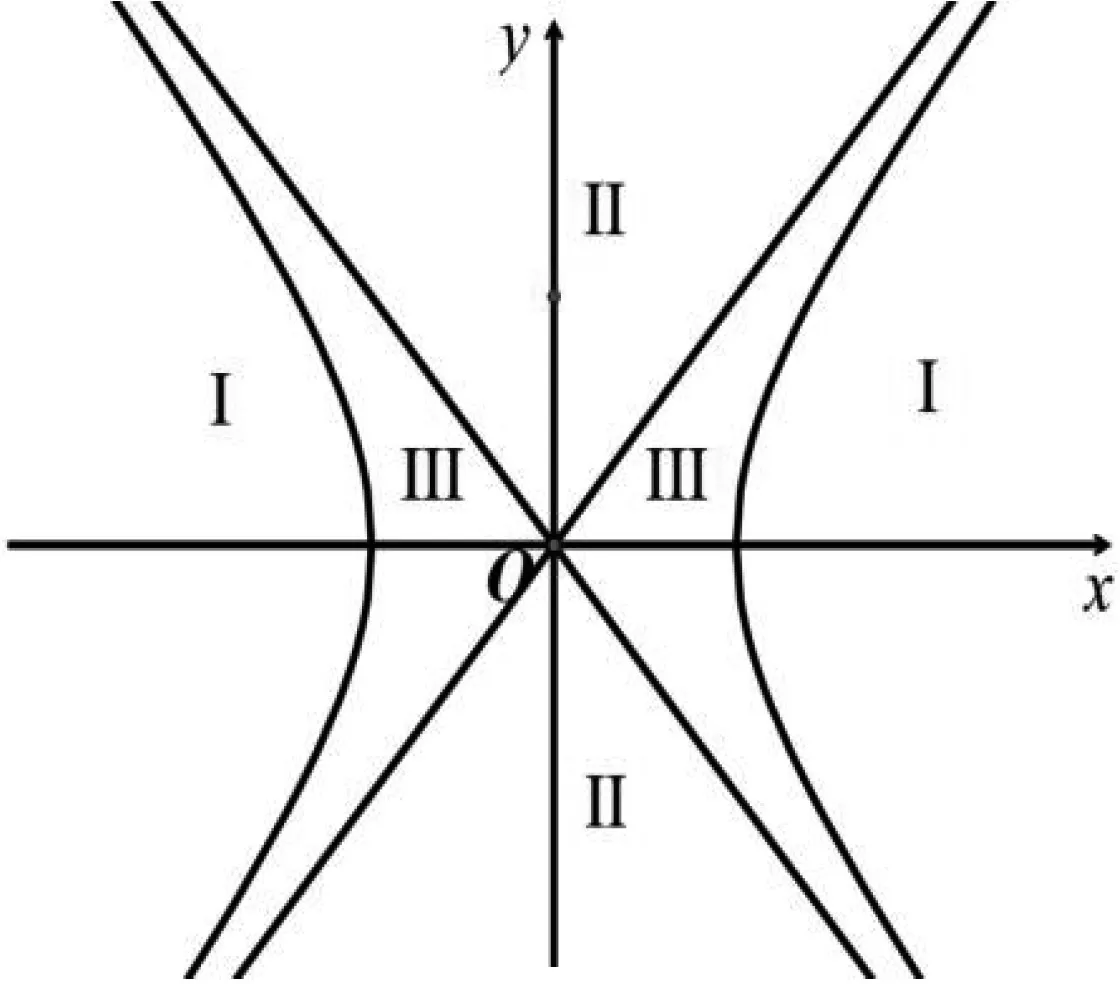
图3

②若点P在双曲线的区域Ⅰ与区域Ⅱ时,Δ>0,此时中点弦存在.

2.3 双曲线的切线条数的区域

问题3 类比直线与椭圆中的研究方法,过一点可作几条双曲线的切线?

以下先来研究(*)式解的情况,同时注意结合斜率不存在时可能存在切线的情况,结论如下:

(1)当x0=±a,y0=0时,(*)式无解,此时还有一条平行于y轴的切线.

(2)当x0=±a,y0≠0且y0≠±b时,(*)式有唯一解,此时有两条切线,其中一条平行于y轴.

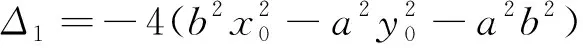
综上所述,由定点所确定的切线条数的区域如下.

结论3 (如图3)①若P在原点O处,或在双曲线内(区域Ⅰ),可作0条切线;②若P在渐近线上(除O外),或在双曲线上,可作1条切线;③若P在双曲线外且不在渐近线上(区域Ⅱ,Ⅲ),可作2条切线.

2.4 与双曲线有唯一公共点的区域

问题4 过点P作与双曲线有唯一公共点的直线有几条?

注意到当直线与双曲线只有一个公共点时,有两种情况:相交(直线与渐近线平行时)或相切.在问题3中已经研究了切线条数的情况,只需研究与渐近线平行的相交直线的条数即可.

当点P在原点O处,有0条与渐近线平行的相交直线;当点P在渐近线上(除O外),可作1条与渐近线平行的相交直线;当点P在双曲线上,或在区域Ⅰ,Ⅱ,Ⅲ,可作2条与渐近线平行的相交直线.

此时再加上问题3中相切的条数,归纳得如下情况(如图3):

结论4 ①若P同时在原点O处,可作0条;②若点P在双曲线内(区域Ⅰ),或在渐近线上(除O外),可作2条;(在双曲线内,此时两条均相交;在渐近线上(除O外),一条相切一条相交).③若点P在双曲线上,可作3条,一条相切,两条相交.④若点P在双曲线外的区域Ⅱ与区域Ⅲ,有4条,两条相切,两条相交.

三、教学反思

在中学数学的学习过程中,抽象思维的要求越来越高,教学时需尊重学生认知思维的发展规律,设置必要的思维梯度.整体看待单元知识,并对单元知识结构进行重组,呈现出环环相扣、层层递进的逻辑链结构,培养由简至繁的思维习惯.例如区域问题的4个层次,从最简单的点与曲线的位置,到中点弦存在区域、再到切线条数区域和唯一公共点区域,情况逐渐复杂,逻辑依次递进,加强了知识之间的内在联系.

此外,借助直观化的方法可适当减轻学生思维的抽象性负担,破解学生的心理障碍.形象思维是人们发现、掌握事物本质的初始能力,数学知识本身就具有丰富的表象.而高中数学的抽象复杂是很多学生比较畏惧的,可借助多感官参与,给学生联想、想象的空间,让形象思维与抽象思维相得益彰.