一类三角函数最值问题的探究

福建省南安第一中学 (362300) 陈佳祥

三角函数最值问题是历年来高考考试中的重点问题,具有涉及范围广、综合性强、灵活性大等特征.因此在解决三角函数最值问题时,需要掌握三角函数的周期性、有界性、单调性等性质,并灵活应用三角恒等变换,结合其函数最值特点进行有效地分析.本文主要讨论形如(1)f(x)=cos2x·sinx;f(x)=cosx·sin2x;f(x)=sinx·sin2x;f(x)=cos2x·cosx;,(2)f(x)=sin3x+3sinx等函数的最值.

1 问题本质

由倍角公式cos2x=2cos2x-1,可知cos2x可以表示为cosx的二次多项式．一般地,存在一个n(n∈N*)次多项式Pn(t)=a0tn+a1tn-1+a2tn-2+···+an(a0,a1,a2,···,an∈R),使得cosnx=Pn(cosx),这些多项式Pn(t)称为切比雪夫(P．L．Tschebyscheff)多项式．运用探究切比雪夫多项式的方法可得cos2x=P2(cosx)=2cos2x-1,记作P2(t)=2t2-1,cos3x=cos(2x+x)=cos2xcosx-sin2xsinx=(2cos2x-1)cosx-2sin2xcosx=(2cos2x-1)cosx-2(1-cos2x)cosx=4cos3x-3cosx,所以P3(t)=4t3-3t,同理可得sin3x=3sinx-4sin3x.

因此问题(1)和(2)本质都可以展开以cosx(或者sinx)的三次多项式,三次函数拥有的对称性、单调性等性质,因此这类三角函数的最值是值得研究.

2 基于“换元法”的导数法求解三角函数最值

当三角函数表达式始终只存在正弦函数、余弦函数,且函数最高次数为“3”时,可通过整体换元的方法将其转化为一元三次函数的最值问题,再结合导数单调性研究最值.

例1 求函数f(x)=cos2xsinx在R上的最大值.

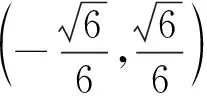
评析：该问题在倍角公式cos2x=1-2sin2x的基础上,通过化归转化的思想,有效地整理与变形,构成只含有sinx的三次多项式的函数,然后换元为一元三次函数形式,需要注意换元的取值范围,再借助一元三次函数导数单调性研究最值.

3 基于均值不等式求解三角函数最值

利用均值不等式求最值,所需的条件可概括为“一正、二定、三相等”.当这些条件不完全具备时,就需要凑“定和”或“定积”的技巧,使其具备.同角三角平方和关系式sin2x+cos2x=1其作为隐含条件,依据三角函数“定和”的特征,求三角函数最值有充分地体现.

例2 设x为锐角,求函数y=sinx·sin2x的最大值.

例3 设ΔABC的内角A、B、C,求cosA(sinB+sinC)的最小值.

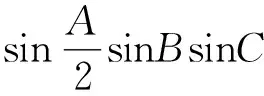
4 基于琴生不等式求解三角函数最值

例4 求函数f(x)=sin3x+3sinx的值域．

例4有如下更一般的形式:

变式2求f(x)=sinnx+nsinx(n∈N+)的值域．

对于三次多项式的三角函数最值问题,一般解题思路是:合理的三角变换或是代数换元,化归为三角函数或者三次函数类型,最后利用导数和基本不等式或琴生不等式方法求最值.引导学生掌握三角函数的单调性、有界性、周期性等性质,再通过函数的最值问题与导数和不等式知识的综合运用,就能有效地解决三角函数的最值问题.