一种舰船摇摆下基于正弦空间的多波束覆盖范围计算方法

赵海东,付 林,贾 然

(中国船舶集团有限公司第八研究院,南京 211153)

0 引 言

舰船航行时发生的纵摇、横摇和航向的改变对雷达的波束指向及空间覆盖影响很大。为了保障雷达系统的指向精度,无机械稳定平台的波束稳定系统一般都采用坐标变换技术[1-2],在雷达天线方位和俯仰轴上对舰船摇摆姿态角进行角度实时补偿,从而实现雷达天线波束指向的电子稳定。

在舰船摇摆运动过程中,阵面坐标系同一俯仰角的多个波束的覆盖范围会随之不断变化,大地坐标系的水平面往往被阵面坐标系的多个俯仰层的不同指向波束覆盖,单个俯仰层的多波束已无法满足对水平面的全覆盖,须计算不同俯仰层在水平面的方位覆盖范围,通过俯仰层组合实现对水平面的组合覆盖。

本文提出一种基于正弦空间[3]的多波束覆盖范围计算方法,利用正弦空间中波束形状不变的特性,计算覆盖水平面的俯仰层以及每个俯仰层下多波束的方位覆盖范围。

1 正弦空间

在大地坐标系下,在波束扫描时相控阵雷达天线的波宽随着其偏离法线方向而展宽,同时波束形状也有所变化,导致波束排列等问题复杂化。正弦空间是单元球面在阵列平面上的投影,如图1[4]所示,阵列平面位于XOY。在正弦空间中,波束的形状不随扫描角变化,有利于对波束覆盖进行分析和编排。在此坐标系下,波束宽度和角位置增量不用度、弧度,而是用其正弦或正弦增量来表示。θ和φ为球坐标系下的波束,α和β为波束在正弦空间中的坐标。

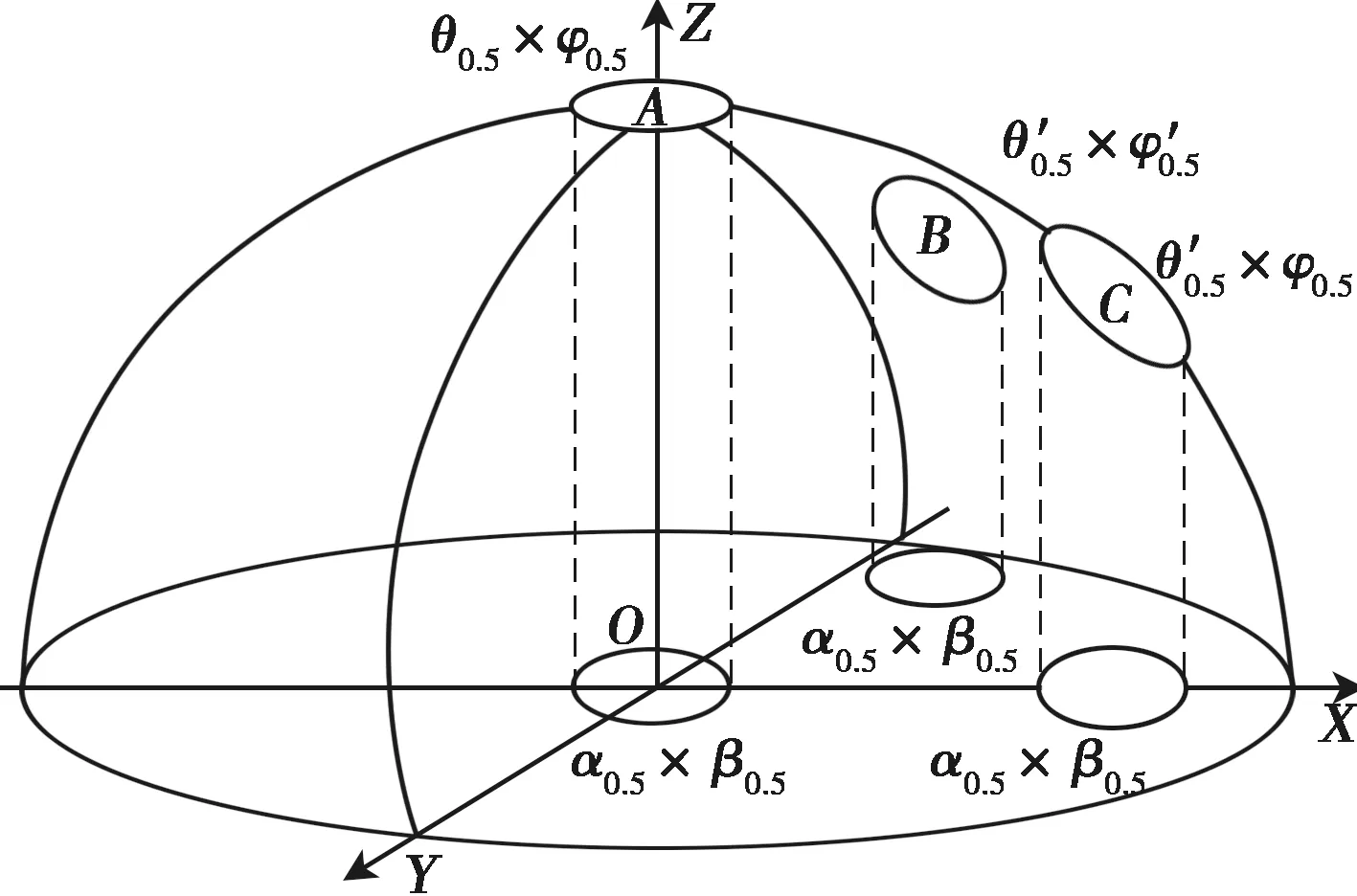
图1 二维平面阵波束投影图

2 坐标系转换

在正弦空间下完成波束编排后,通常用阵面坐标系表示波位信息,而波束的实际覆盖范围则须要转换至大地坐标系,涉及到正弦、阵面、大地3个坐标系间的转换[5]。

(1)大地坐标系与阵面坐标系的转换

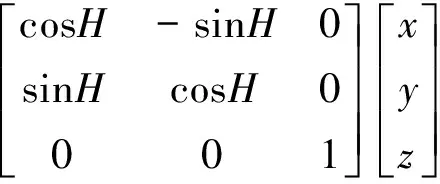
(1)

式中,H为航向角;P为纵摇角;Rl为横摇角;Q为面阵安装角;C为面阵倾斜角;(x,y,z)为波束在大地直角坐标系下的坐标,对应的大地球坐标系(图2)可表示为

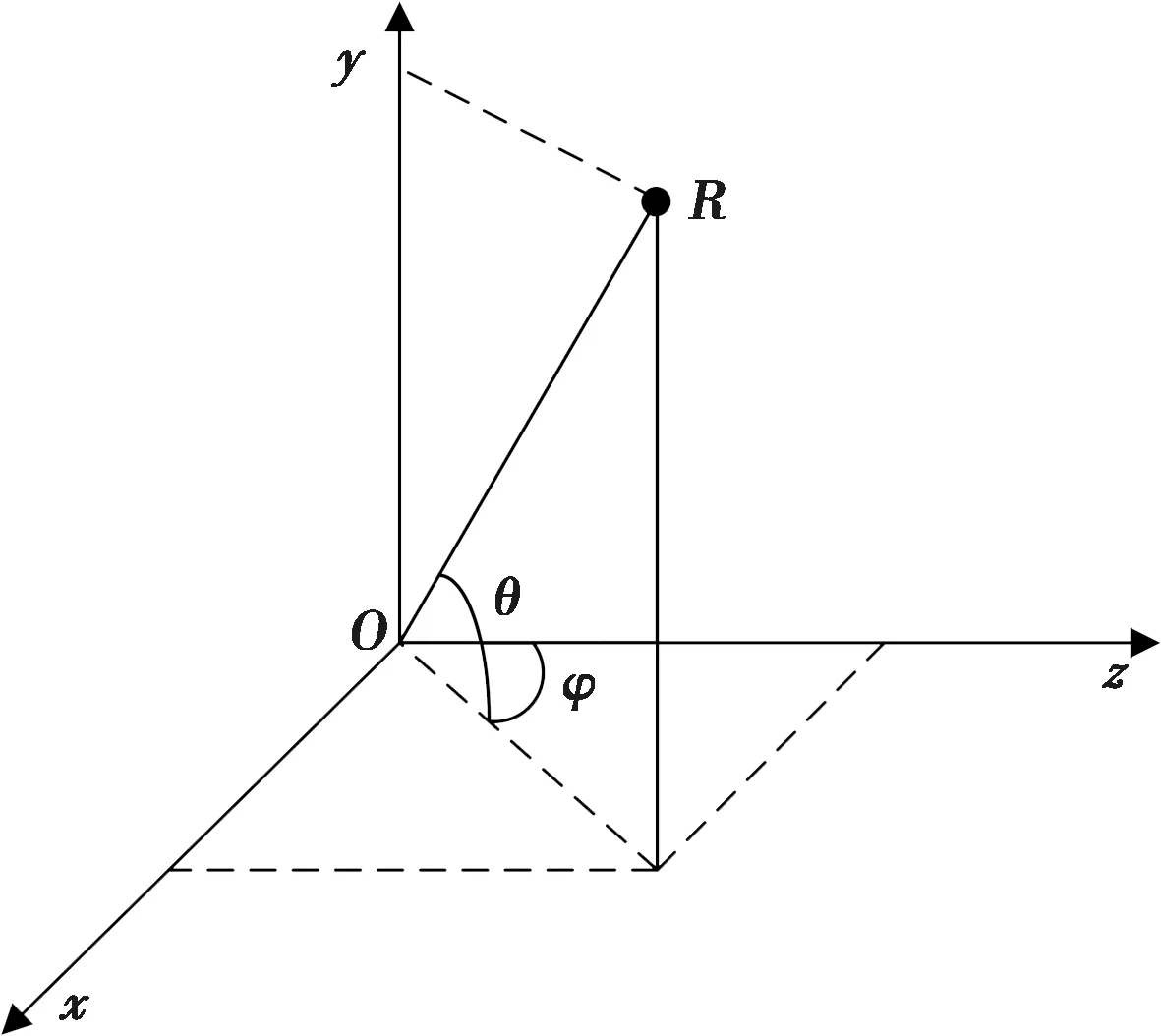
图2 大地球坐标系

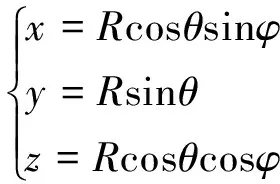
(2)

(xa,ya,za)为波束在阵面直角坐标系下的坐标,其对应的阵面球坐标系(图3)可以表示为

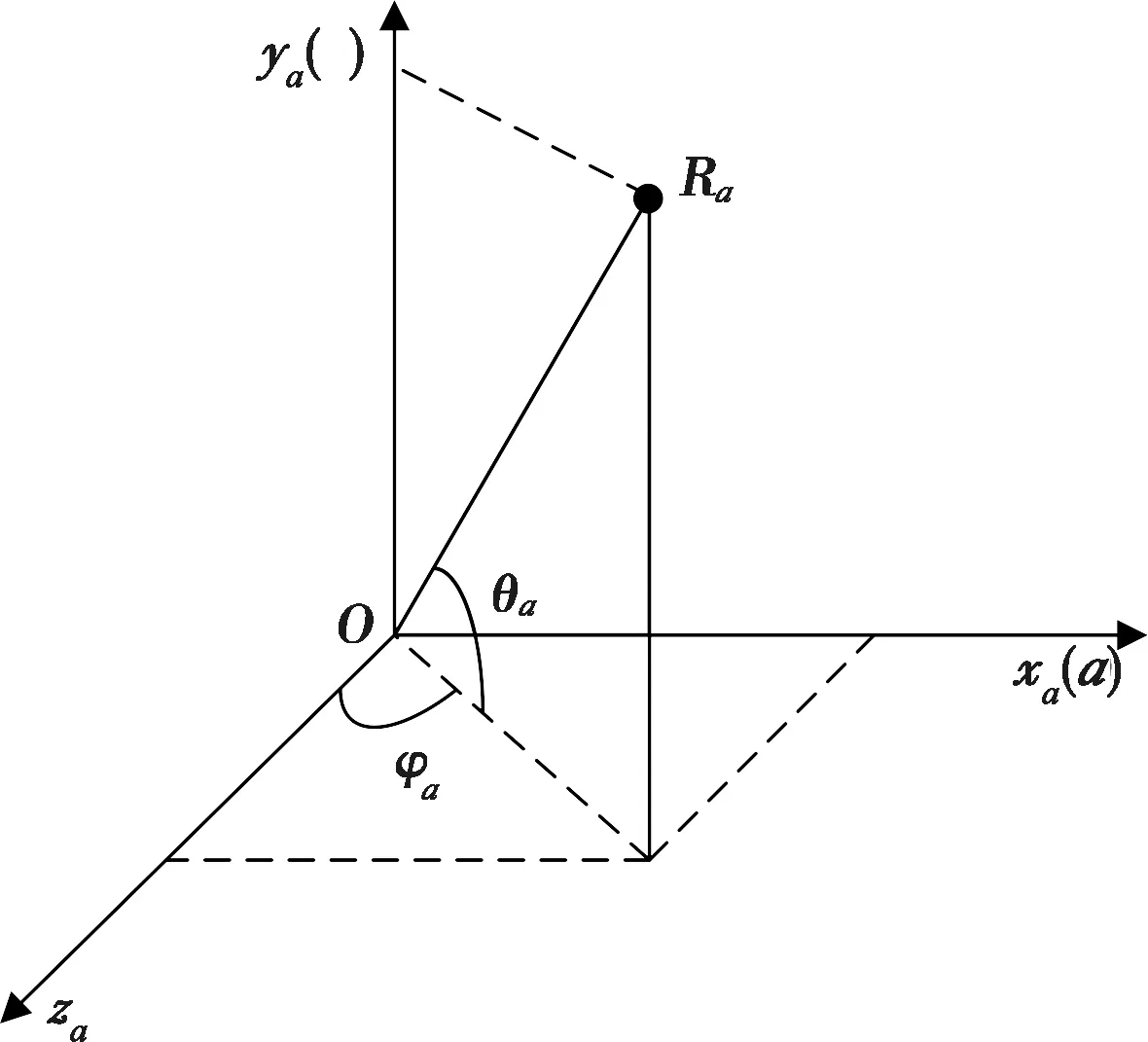
图3 阵面球坐标系

(3)

(2)阵面坐标系与正弦坐标系的转换

如图3所示,阵面位于xaoya平面,xa即为正弦空间的α轴,ya为正弦空间的β轴,由此可得转换关系:

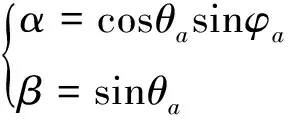
(4)

利用式(1)～(4)即可完成大地坐标系与正弦坐标系之间的转换。

3 覆盖范围计算

在正弦空间中,可以通过计算某一坐标点与各波束之间的中心距离来确定此坐标点的覆盖波束,本文通过此方法将水平面映射至正弦空间中,并按等间隔取点计算来选取覆盖波束。具体步骤如下:

(1)确定面阵法线指向的大地方位AZ_Center,将大地坐标(AZ_Center,0)转换至正弦空间中,得到初始点坐标(α0,β0),通过计算距离得到距离最近的波束,即此波束覆盖(α0,β0),将该波束的俯仰层作为初始俯仰层k0;

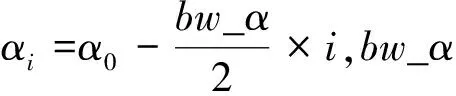
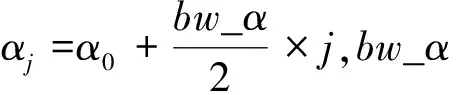
(4)合并第(2)、(3)步的计算结果,得到初始俯仰层k0在大地水平面的覆盖范围为[A0,B0];

(5)以第(2)步的终止坐标点为起始点,记此点俯仰层kn,n=1,2,3,…。同第(2)步一样,依次选点往左计算,直至俯仰层变化时,将上一个坐标点和当前坐标点的中心值作为计算点,该点的大地方位即为俯仰层kn在大地水平面覆盖范围的左边界An。俯仰层kn在大地水平面覆盖范围的右边界Bn为上一俯仰层的左边界。俯仰层kn在大地水平面的覆盖范围为[An,Bn]。当坐标点超过面阵覆盖范围左边界时,停止往左计算;

(6)以第(3)步的终止坐标点为起始点,记此点俯仰层km,m=n,n+1,n+2,…。同第(3)步一样,依次选点往右计算,直至俯仰层变化时,将上一个坐标点和当前坐标点的中心值作为计算点,该点的大地方位即为俯仰层km在大地水平面覆盖范围的右边界Bm。俯仰层km在大地水平面覆盖范围的左边界Am为上一俯仰层的右边界。俯仰层km在大地水平面的覆盖范围为[Am,Bm]。当坐标点超过面阵覆盖范围右边界时,停止往右计算。

4 仿真验证

根据以上算法,设置仿真参数如表1所示。

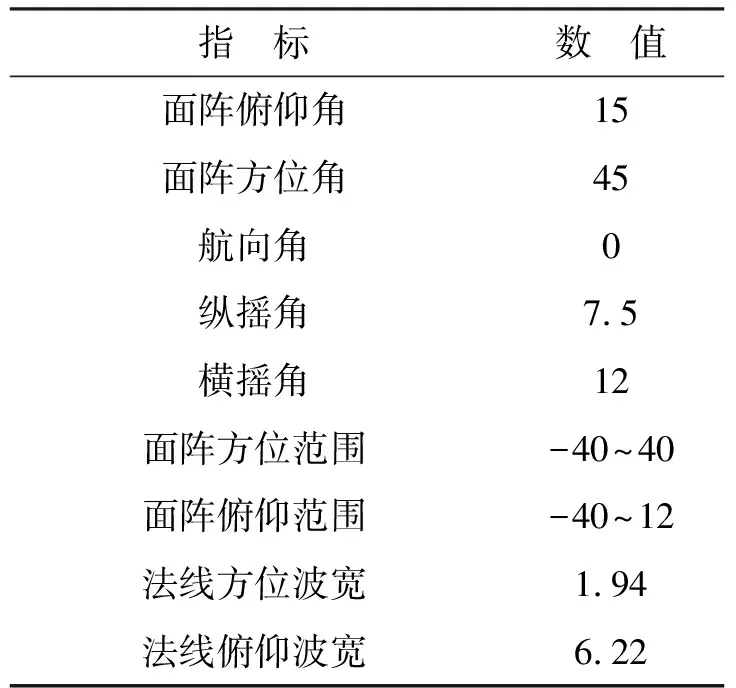
表1 仿真参数(单位:°)

将大地水平面映射至正弦空间中,结果如图4所示,图中‘+’表示在正弦空间中按照等间隔计算所选取的点。通过距离计算判断俯仰层的覆盖情况,结果如表2所示。

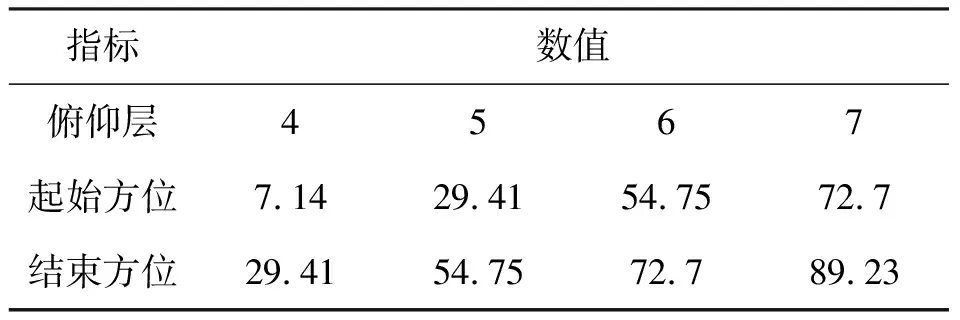
表2 计算结果(单位:°)

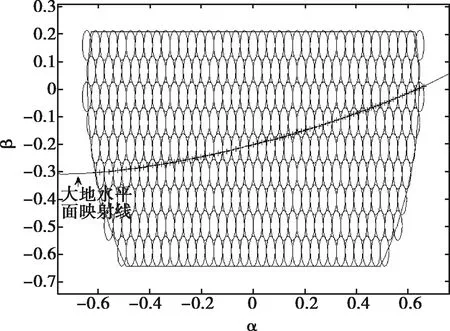
图4 正弦空间下的波束分布

将上述结果的方位在大地坐标下画出,结果如图5所示,俯仰层从下往上记为俯仰层1,俯仰层2,…,俯仰层9。利用该方法计算出的覆盖范围与各俯仰层的实际水平面覆盖范围相吻合,验证了该方法的有效性。

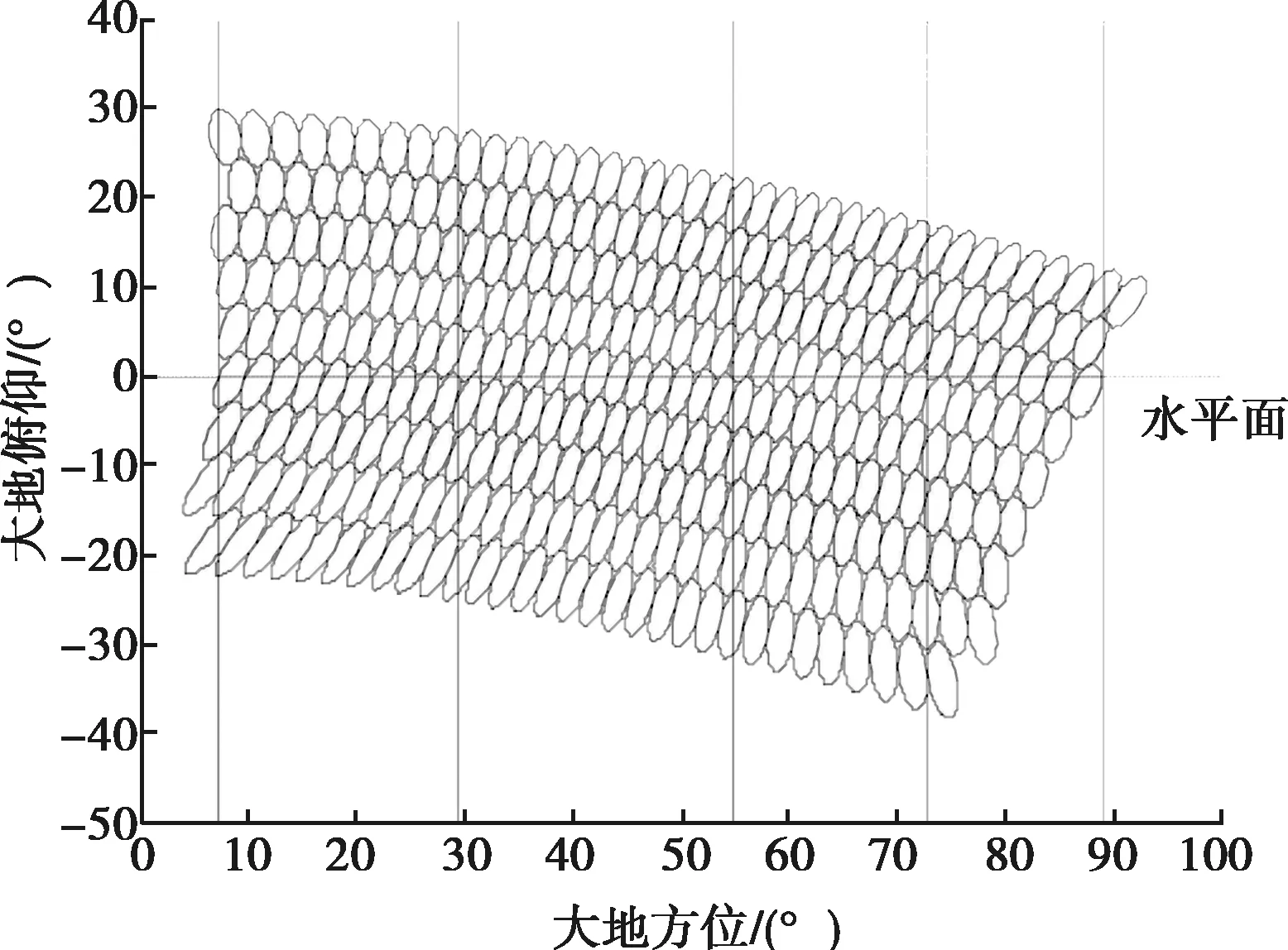
图5 大地坐标下的波束覆盖情况

5 结束语

本文针对舰船摇摆时多波束覆盖范围的不断变化,提出了一种利用正弦空间中波束形状不变的特性来计算多波束大地方位覆盖范围的方法,该方法将大地水平面映射至正弦空间中,通过在水平面映射线上按等间隔取点计算各俯仰层的覆盖范围,最后通过仿真实验验证了该方法的有效性,可为舰船摇摆下的波束调度提供理论依据。