连续凸逼近加权自相关波形优化方法

2023-09-28 07:12宋青青

雷达与对抗 2023年3期

张勇,宋青青

(1.南京六九零二科技有限公司,南京 210009;2.中国船舶集团有限公司第八研究院,南京 211153)

0 引言

波形设计是当前最热门的雷达系统技术研究领域之一。有源探测与通信系统均对具有良好自相关特性的波形序列有着十分迫切的需求,例如脉冲压缩雷达系统收发信号、声纳探测器编码序列与数字通信系统(如GPS接收器或CDMA蜂窝系统)的同步、信道估计的导频序列,甚至安全系统的密码学[1-5]。在实际应用中,由于序列生成硬件的限制(如信号最大幅度/功率起伏须保持在模数转换器和功率放大器动态范围内),通常要求发射波形具有恒模特性。

近年来,恒模序列(也称为多相序列)因具有强相关可塑性、高能量利用率等特点而备受关注[6-7]。相位编码序列的获取途径主要包括固定计算(如Barker码、Frank码等)与迭代优化(如遗传算法、CAN算法等优化架构)[8]。

经典的Barker码序列属于二进制编码序列,可由移位寄存器或综合逻辑法得到,具有较好的自相关特性,自相关峰值旁瓣电平不高于1,但其序列编码长度较有限,现阶段不超过13。1965年,Golomb和Scholtz开展了广义Barker码研究,仍遵循最小化峰值旁瓣比原则,扩展了编码元素集,寻求具有类似Barker序列自相关特性的相位编码序列。以此为驱动,关于广义Barker码序列的研究不断深化,序列长度扩展至77。是否存在更长的广义Barker序列当前仍未得到证实。除了Barker序列,还存在多相码簇可由闭式解析式得到,如Frank码、Golomb序列。随着序列长度的增加,该类序列峰值旁瓣比增长速度与序列长度的平方根成正比,与Barker码自相关特性差异化明显。

随着数字技术的发展,波形码元集不断得到扩充,码型序列的复杂度呈指数上升态势。面向复杂波形序列对强设计规则鲁棒性、高算法通用性的需求,迭代优化类算法应运而生,主要包括遗传算法(Genetic Algorithm,GA)、模拟退火等全局寻优、变换域优化、乘子类等算法。GA最早是由美国的John Holland于20世纪70年代提出,是一种借鉴生物进化规律的结构化搜索全局最优解的方法[9]。由于复杂波形全局寻优的可行集巨大,该方法虽然不需要引入复杂的推导计算,但对于高维向量优化存在计算量大、耗时长的缺点,不利于波形集的快速更新。模拟退火算法(Simulated Annealing,SA)[10]思想最早由N Metropolis等人于1953年提出。在此基础上,S Kirkpatrick等人于1983年将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性,与遗传算法一样采用结构化优化架构,计算量巨大,亦不适合高维向量优化,对长度大于等于103量级的序列优化是不实际的。为了适应高维度波形优化,文献[11]和[12]为了最小化自相关积分旁瓣(Integrated sidelobe level,ISL),采用其“几乎等效”的频域表达为目标函数,借助快速傅里叶变化提出了高效的CAN算法及加权循环算法(Weight cyclic algorithm new,WeCAN),可实现长度不低于104的多相码序列的快速优化,远超Frank与Golomb序列长度。基于上述ISL等效结果,以交替优化为代表的乘子类算法[13]逐渐应用在低ISL波形优化中。峰值旁瓣(Peak sidelobe level,PSL)水平是另外一种较为常用的自相关副瓣考核指标,具有瞬变的特点,相比于以ISL为目标函数的波形设计问题,以PSL水平为优化目标的优化问题更加难以驾驭,近端梯度下降法[14]解决了包含多个等式与不等式共存的非凸优化问题,实现了低峰值旁瓣比的波形优化设计,但该方法对于子梯度选取具有不确定性,算法结果较难把握,而且对于自相关局部最小化问题无法求解。相比于PSL,以ISL为目标函数更适合快速、可靠波形设计的应用场合。

文献[11]使用了等效加权积分旁瓣为目标函数,无法使其与ISL概念完全一致,最优解的ISL无法得到保证。本文以最小化自相关加权自相关副瓣积分为目标函数,对原非凸优化问题目标函数经过连续两次凸逼近,并将模量约束松弛为能量约束,使得原问题转化为凸问题,利用成熟优化技术对其求解。最后,将最优解进行幅度强制归一化处理,获得适用于饱和功放等器件使用的恒模波形序列,其中可通过调整权值分布对自相关形状进行有效控制。

符号说明:本文采用粗体小写字母表示矢量,用粗体大写字母表示矩阵;(·)T、(·)H分别表示矩阵与向量的转置和共轭转置算子;| |、‖ ‖分别表示取输入参数的绝对值和l2范数;字母j为虚数单位;M和M分别表示M维实数向量和复数向量;M×N和M×N分别表示M×N维实数和复数矩阵;Tr(·)表示计算输入矩阵的迹。

1 信号模型与问题构建

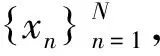
(1)

加权积分旁瓣电平γ为

(2)

式中,w为加权系数向量,其向量形式为

w=[w1,w2,…,wN-1]T

(3)

当w为全1矩阵时,γ与常规积分旁瓣电平的含义相同。雷达、通信系统均需要低自相关旁瓣电平的波形序列。在实际电磁辐射系统中发射能量通常是一定,在此约束下,以最小化积分旁瓣电平为目标函数,构建优化问题为

(4)

若要实现自相关函数局部区域趋零或置零,则须适当增加w中相关区域对应的权值,权值增加,该区域对目标函数取值影响增大;反之易然。

2 连续凸逼近算法

由于目标函数为非凸的,使用常规优化算法难以解决。为了解决式(4),拟将寻找目标函数凸上界函数,并将其作为目标函数,构建等效优化问题进行求解。

为便于阐释,采用矩阵表示式(4),则自相关函数矩阵形式为

rk=Tr(ΕkxxH),k=0,…,N-1

(5)

式中,Εk∈N×N为第k对角线全为1的Toeplitz矩阵。

则式(4)可进一步表示为

(6)

|xn|=1,n=1,…,N

由于自相关函数r的模值具有对称性,因此式(6)可等价为

subject toX=xxH

(7)

|xn|=1,n=1,…,N

此时,w维度扩展为2N-1,完整表达式为

w=[w1-N,…,0,…,wN-1]T

(8)

且w0=0,w-k=wk。

将式(7)目标函数中的矩阵向量化后,经推导,式(7)目标函数可表示为

(9)

令xv=vec(X),ek=vec(Ek),则式(7)可重新整理为

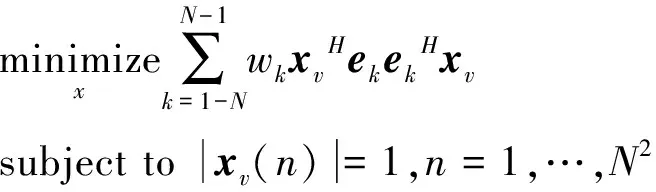
(10)

假定

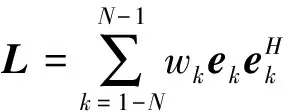
(11)

则可将式(10)中的目标函数化简为二次型,即

(12)

为了最小化非凸目标函数,可通过最小化其上边界凸函数,达到原目标函数最小化的目的。假定Q=λmax(L)I,因此(Q-L)为半正定矩阵,λmax(L)为L的最大特征值。结合L的特殊结构,根据方阵特征值与特征向量的定义,可知

因此,ek为属于L的第k个特征向量,且wk(N-|k|)为特征向量ek对应的特征值。可通过比较所有wk(N-|k|),k=0,1,…,N-1值确定L的最大特征值。

略去第一项与第三项常数部分,式(12)可重新构建为

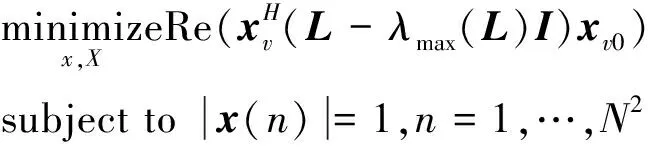
(15)

再将xv0、xv和L均还原为矩阵表达式,即

(16)

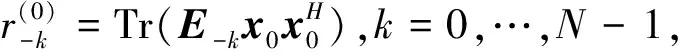
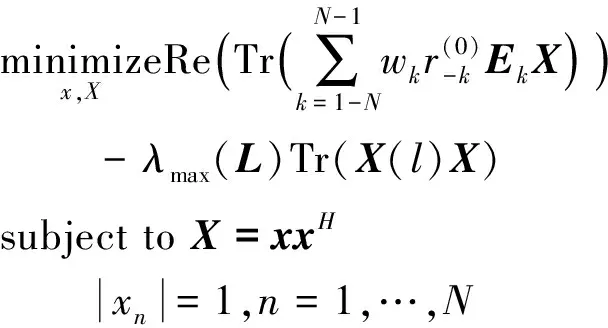
(17)

为求解波形序列x,须将其显性表示,故将X还原为向量形式,优化式(17)可得

(18)

式中,

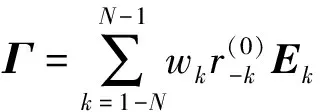
(19)

忽略常数项后,式(18)可转化为

subject to|xn|=1,n=1,…,N

(21)

式中,λg为Γ的最大特征值。

优化式(21)目标为线性函数可示为凸函数,然而由于恒模约束的存在,该问题仍为非凸优化问题,难以直接求解,因此将优化式(21)的约束进行放松,可得

(22)

求解优化式(22)后,可取其最优解的相位向量,重新构成恒模向量作为最终波形序列。具体算法流程可见表1。

表1 连续凸逼近加权自相关波形优化算法流程

3 数值仿真

本节将连续凸逼近加权自相关波形优化算法与现有的WeCAN算法进行比较,验证所提算法的有效性,开展了针对常规低副瓣波形和加权ISL波形的设计性能验证。仿真参数设置:非周期波形序列长度为32、128;最大迭代次数15 000次;终止常数10-6;计算机配置为Intel(R)Core(TM)i5-7500 CPU @ 3.40 GHz,内存4 G。

本节从常规低副瓣波形设计入手,给出了恒模波形序列的相位、自相关函数,并采用数值分析方法比较了WeCAN算法与连续凸逼近加权自相关波形优化算法的收敛性能。进一步,针对加权自相关波形优化,验证所提算法的可行性,同样从以上三方面进行阐释比较,证明所提算法的优越性。

(1)常规低副瓣波形设计

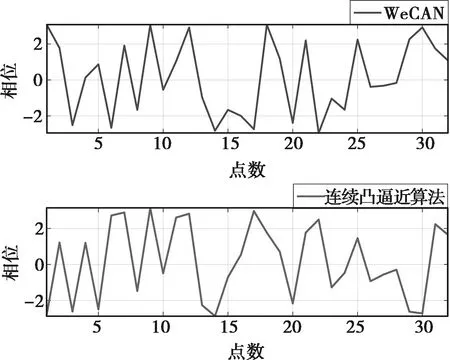
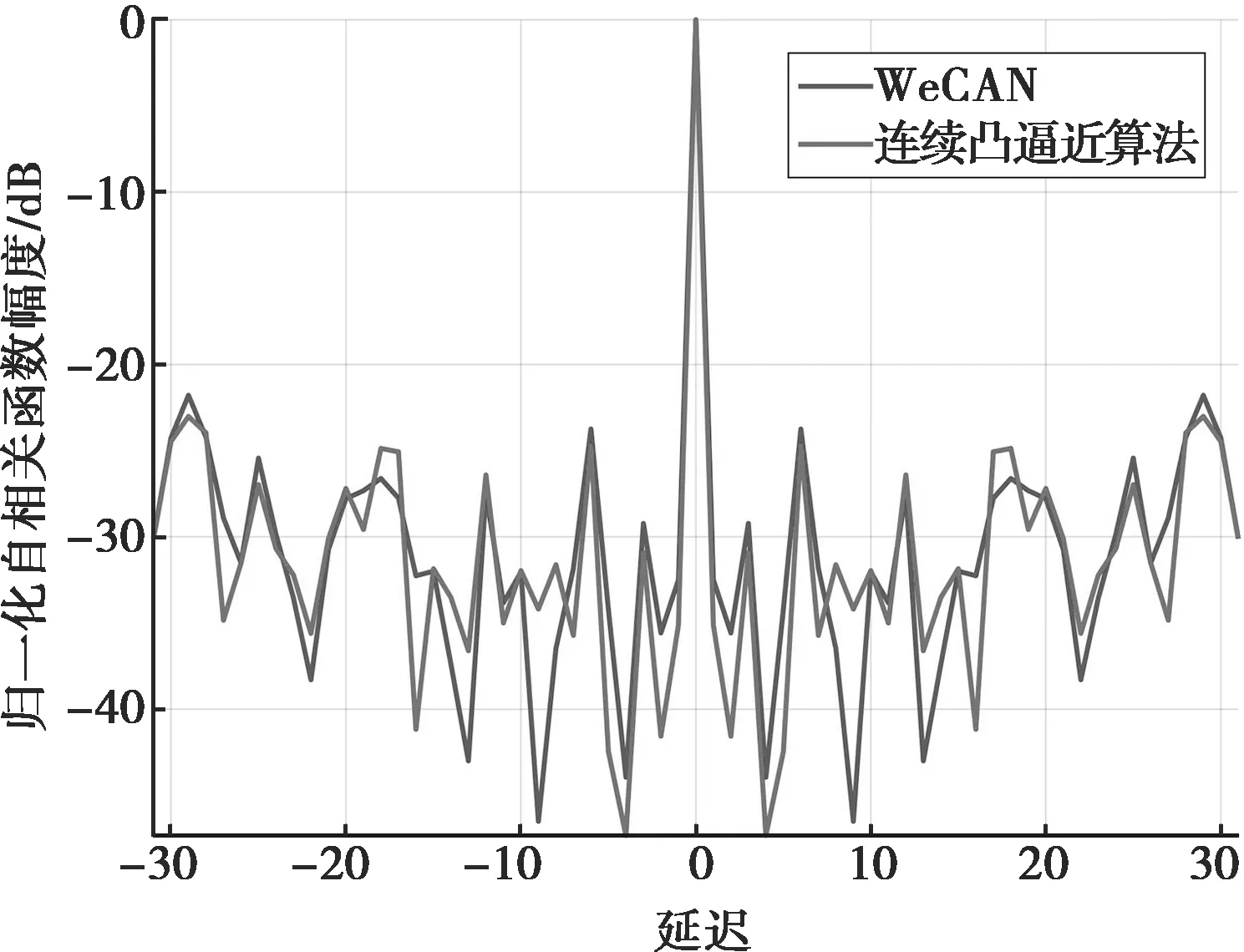
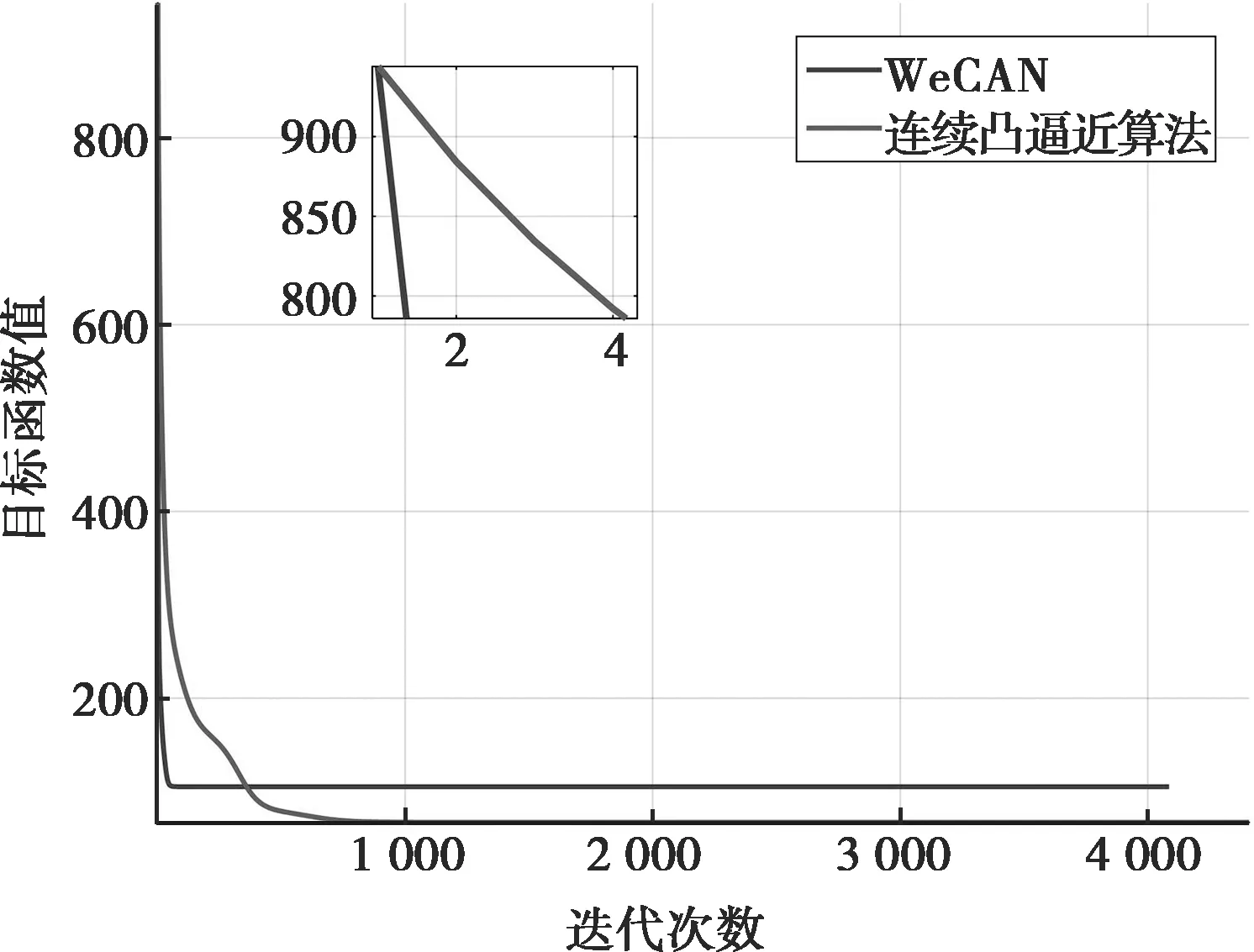
常规低副瓣波形设计时权值设置为相同值。图1(a)、(b)分别给出了长度分别为32、128时WeCAN和连续凸逼近算法所得常规低副瓣波形的相位,二者存在较大差异,且类似随机噪声信号。图2(a)、(b)分别给出了长度32、128时两算法所得的低副瓣波形自相关函数,长度相同时两算法对应最优波形的自相关函数水平几乎一致。图3(a)、(b)分别给出了波形序列长度为32和128时,WeCAN与连续凸逼近加权自相关波形优化算法的收敛曲线。从中可看出,WeCAN收敛速度优于本文所提算法,此时频域等效方法优于时域直接优化方法。

(a)长度32

(2)加权副瓣波形设计

加权副瓣波形设计时,须先确定距离向干扰或杂波所处的距离段,再通过增加自相关函数中相应延迟部分的权值,达到抑制干扰/杂波距离向处理增益的效果。参数设置如表2所示。

表2 加权自相关波形优化算法参数设置

图4(a)、(b)分别给出了长度分别为32、128时WeCAN和连续凸逼近加权自相关波形优化算法所得加权自相关副瓣波形的相位。图5(a)、(b)给出了长度分别为32、128时两算法所得的加权副瓣波形自相关函数,长度相同时两算法对应最优波形的自相关函数形状一致,但凹口处连续凸逼近算法对应的电平低于WeCAN,可以获得更好的距离向干扰、杂波的抑制效果。图6(a)、(b)分别给出了波形序列长度为32、128时,WeCAN与连续凸逼近算法的收敛曲线。从中可看出,本文所提连续凸逼近加权自相关波形优化算法优于WeCAN算法的收敛速度,且稳定收敛时连续凸逼近算法目标函数对应的最优值低于WeCAN算法,故而相比于WeCAN算法,本文所提算法获得理想的凹口深度。