基于神经网络的钻井液漏失裂缝宽度预测研究

王 健，徐加放,2,3，赵密福，王博闻，王亚华，陈 杰，王潇辉，杨 刚，马腾飞

(1.中国石油大学(华东)石油工程学院，山东 青岛 266580；2.油气钻完井技术国家工程研究中心，山东 青岛 266580；3.非常规油气开发教育部重点实验室，山东 青岛 266580；4.中国石油化工股份有限公司东北分公司，吉林 长春 130000；5.中联煤层气有限责任公司，北京 100011)

在钻井过程中，由于压差作用钻井液往往通过裂缝渗透进入地层造成钻井液漏失，或者进入储层导致储层污染，尤其是煤层气储层，裂缝层理发育，在钻井时极易受到污染[1]。对于这一现象，通常的方法为在钻井过程中根据钻遇地层裂缝大小选择相应的封堵材料，对缝隙进行封堵，从而降低钻井液滤失[2]，因此对漏失裂缝宽度进行预测极为重要。

目前传统的测定储层裂缝宽度的方法主要有测井识别、经验法以及模型计算等。其中，测井识别是在钻井过程中通过测井来获取天然裂缝宽度的相关数据[3-4]，但是其无法测得钻进过程中裂缝的变化且在井漏时操作较为困难。经验法主要是根据以往的堵漏经验来判断储层裂缝宽度，但是很难保证其成功率[5]。模型计算是通过建立相应的漏失模型对裂缝宽度进行计算，如以牛顿流体为研究对象建立的平均宽度Sanfillippo 模型[6]以及相应的改进模型[7-8]等，虽然数学模型计算发展较快，但是其运用的公式较为复杂且需要的储层参数不一，适应范围有限，现场应用困难，需要一种较为简单且适应范围广的裂缝预测模型。

随着人工智能的发展，一些学者利用人工智能方法对储层裂缝进行预测[5-9]并取得了不错的效果，但大多只利用了单一的预测模型或单一的优化模型，没有考虑对其进行系统优化以提升模型的预测精度，而随着智能算法的发展，很多优化算法和集成算法被应用到人工智能预测当中，使得模型的预测能力与精度大大提高[10-11]。

鉴于此，笔者利用遗传算法(GA)和Adaboost 算法对BP 神经网络(BPNN)进行优化以提高其预测性能，建立了Adaboost-GA-BP 神经网络裂缝宽度预测模型，对裂缝宽度进行预测，为钻井过程中钻井液漏失的裂缝宽度判断和堵漏剂的选择提供一定的指导。

1 Adaboost-GA-BP 神经网络预测模型

1.1 BP 神经网络

BP 神经网络是利用误差反向传播来进行训练的多层前馈网络，应用范围十分广泛，其网络结构由3 部分组成：输入层、隐含层和输出层。输入参数从输入层输入，经过隐含层的进一步处理，最后由输出层输出预测结果。另外，单隐含层的BP 神经网络预测模型可以拟合逼近非线性函数，达到很高的预测精度[12]，因此本文采用单隐含层的BP 神经网络作为基础的预测模型，其具体结构如图1 所示。

图1 神经网络结构Fig.1 Neural network structure

虽然BP 神经网络具有很高的预测能力，但是其在训练过程中初始权值和阈值是随机选择的，选择不当会使得模型陷入局部极小值而无法达到全局最优[13]，因此需要对其进行优化。

1.2 遗传优化算法

遗传算法是模拟自然界中生物进化的一种全局优化方法，具有较好的全局寻优能力[14]，可对神经网络的权值和阈值进行优化，找到全局最优解。因此，利用遗传算法对BP 神经网络的权值和阈值进行相应的优化，使预测精度进一步地提升，其算法具体流程如图2 所示，整体步骤如下[15-16]。

图2 遗传算法优化BPNN 流程Fig.2 Optimization process of BPNN by genetic algorithms

(1)初始化设置。设定交叉和变异概率、最大迭代次数、种群规模等参数并初始化种群。

(2)适应度计算。计算每条染色体适应度值并进行排序，其适应度计算公式[17]如下：

式中：E为适应度值；yi、di分别为第i个数据的实际值和预测值，N为训练样本数。

(3)选择操作。依据个体的适应度值大小对种群进行选择，淘汰适应度差的个体。

(4)交叉和变异操作。从步骤3获取的个体中，以交叉和变异概率进行交叉和变异操作，形成新的群体。

(5)重新计算适应度值。计算步骤4得到个体的适应度值，同时将新产生的染色体带入到原种群中，得到新种群。

(6)终止条件判断。计算个体的适应度值是否满足精度要求，若满足则优化完成，否则重复步骤2—步骤6 进行循环计算，直到满足精度要求或迭代次数达到最大设定值，则停止迭代。

1.3 Adaboost 算法

Adaboost 算法是一种迭代算法，属于自适应增强算法。其算法的思想是通过合并多个“弱”预测器的输出，产生有效预测[18]，其算法具体流程如图3 所示，其主要步骤[19]如下。

图3 Adaboost 算法流程Fig.3 Adaboost algorithm flowchart

(1)确定弱预测器的模型和相应的数据，并给每组训练数据一个初始权重。

(2)利用训练数据对弱预测器进行迭代计算，按照每次迭代的结果对训练数据的权重进行更新，对于预测效果差的数据赋予更高的权重以使这些数据在下一次迭代运算时得到更多关注。

(3)通过对弱预测器的反复迭代计算出预测函数序列，每个预测函数都有相应的权重，结果越好的预测函数对应的权重越大。

(4)经过数次迭代后，通过弱预测函数的加权得到强预测器的函数。

2 数据分析与处理

选取合适的地层裂缝特征参数对于预测结果的准确性至关重要。地层裂缝宽度与许多因素有着较为密切的关系，影响因素较为复杂。首先，漏失速度和漏失量与地层裂缝宽度有着直接的关系，钻井液的漏失速率随裂缝宽度的增加而增加[20]，单位时间内的漏失量也随之增加。另外，钻井液密度高，静切力以及塑性黏度大，会使得钻井液中的网架结构遭到破坏，有效液柱压力与地层之间产生压差，会造成井筒周围的裂缝发生变化[21]。O.Lietard 等建立的Lietard 模型总结出了塑性黏度，钻井液漏失速度以及裂缝宽度之间的关系[22]。泵压的变化也会对井底压力产生影响，进而使得裂缝宽度发生变化，而随着井深的增加，地层压实作用越大，裂缝宽度越小。钻速过快会使得井底产生压力波动，使得井筒周围的裂缝产生扩展。通过查阅相关资料[23]，收集选取了91 组钻井过程中与地层裂缝宽度有关的井史资料，包括漏失量、井深、塑性黏度、钻井液静切力、泵压、漏失速度、钻速、排量共8 个参数。为了探究上述因素对裂缝宽度的影响程度，找出其中的主要影响因素，利用斯皮尔曼相关性分析方法对所有参数之间的相关性进行了计算分析，结果如图4 所示。

图4 裂缝影响因素相关系数矩阵Fig.4 Correlation coefficient matrix of influencing factors of cracks

由图可知，与裂缝宽度相关性最强的是漏失速度与漏失量，分别为0.932 和0.924，其他因素与裂缝宽度的相关性相比较弱，从高到低依次为：泵压、钻井液排量、钻速、井深、塑性黏度以及钻井液静切力。其中，钻速、漏失速度和漏失量以及钻井液静切力呈正相关，井深、塑性黏度和泵压和钻井液排量呈负相关，由于钻井液静切力与裂缝宽度相关性较低，仅为0.087，因此模型输入参数不考虑这一因素，选取其他7 种因素作为输入参数，其数据特征见表1。

表1 参数的数据集特征Table 1 Data set characteristics of parameters

由表1 可知，各个参数跨度较大，如井深范围为229～3 750 m，涵盖了不同的地层，其他参数如钻速和漏失量等跨度范围也都比较大，可使得训练出的模型适应不同的情况。把数据分成训练数据和测试数据，64 组数据作为训练数据对模型进行训练，剩余27 组数据作为预测数据，不参与模型的建立及训练，只用于对建立好的模型进行测试，评价其预测效果。另外，由于各个参数的单位不同，其数量级差别较大，如井深与塑性黏度等，这会影响预测模型的预测效果。对此，为消除不同参数之间数量级差别大的影响，本文对数据进行归一化处理[24-25]，使得各参数在区间[0,1]内，其归一化公式如下：

选择了两种用于评价模型预测效果的指标，分别为相关系数(R2)和均方根误差(ERMS)，其计算公式[26]如下：

式中：yi为实际值；为对应的预测值；n为样本个数。

3 神经网络改进与参数选择

在本研究中，附加动量算法和变学习率算法被用来提高模型的训练效率。此外，神经网络模型的准确性受到传递函数和隐含层节点数的影响，因此，本文对隐含层节点和传递函数进行了选择分析以确定最优的模型结构，为后续优化研究打下基础。

3.1 附加动量算法和变学习率算法

传统的BP 神经网络预测模型采用如下式所示的梯度校正方法来更新权重和阈值，该算法没有考虑先前经验的积累，导致学习过程收敛速度较慢。本文采用如下式(6)所示的附加动量算法增加了以往经验的积累，有效地调整了权重和阈值，加快了收敛速度。

式中：w(δ)、w(δ-1)、w(δ-2)分别为δ、δ-1、δ-2时刻的权重值；α为动量学习率。

此外，学习率对预测模型的收敛性也有一定的影响。在神经网络训练过程中，学习率通常是一个固定值，学习率越大，权值的修改就越大，网络学习速度就越快。然而，过大的学习率会使权重在学习过程中产生振动，但过小的学习率使得网络收敛速度慢，无法快速拟合[27]。对于这一问题，本文采用如下式所示的变学习率算法对学习率进行实时调整。在网络进化的早期阶段，学习率较大，网络收敛较为迅速，随着迭代步数的增加，学习率不断下降，网络逐渐稳定。

式中：λ(t)为当前学习率；λmax为最大学习率；λmin为最小学习率；tmax为最大迭代次数；t为当前迭代次数。

附加动量算法和变学习率算法可以显著加快训练过程的学习速度，为了证明该方法的有效性，本文对训练过程中的训练数据的绝对误差和的变化进行了比较分析，结果如图5 所示。

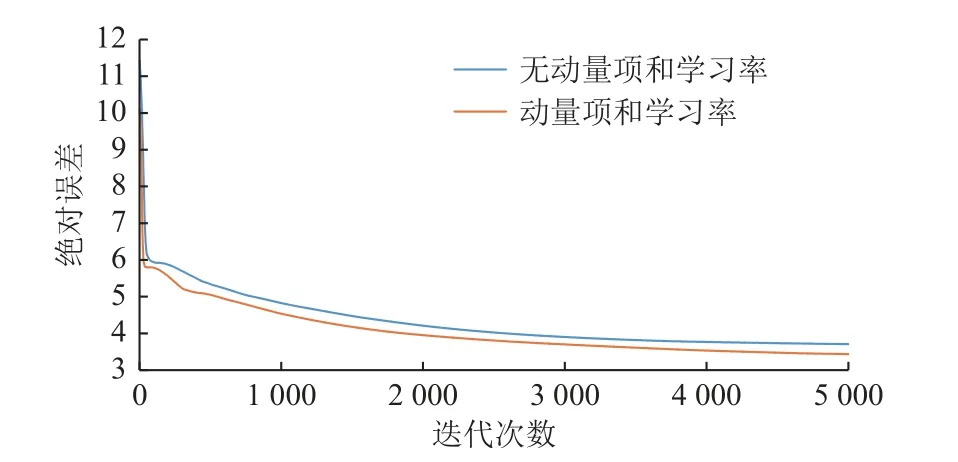
图5 训练过程中误差变化的比较Fig.5 Comparison of error changes during training

图5 中的曲线表示训练过程中随着迭代次数的增加，训练数据绝对误差的变化情况，误差越低说明其下降速度越快，训练效果越好。从图5 可以看出，添加了附加动量算法和变学习率算法后误差显著下降，降低值在25%左右，训练结束时误差降低了27%，表明附加动量算法及变学习率算法可以大大提高学习效率，加快收敛速度，提高模型性能。

3.2 神经网络隐含层节点数选择

神经网络隐含层的节点数对预测模型的性能有较大的影响，节点过少会造成模型鲁棒性较低，无法完全反映输入与输出参数间的关系，而节点过多会造成过拟合和训练时间的增加。对此，本文使用下式所示的经验公式[28-29]对隐含层节点数进行选择。

式中：k是隐含层的节点数；ω和m分别为输入和输出层的节点数；β为介于1 和10 之间的整数。

通过计算可知，隐含层最佳节点数在区间[3,13]内，通过减枝法，对每个隐含层节点数对应的模型进行测试，其误差和相关系数如图6 所示。

图6 不同隐含层节点数的误差及相关系数Fig.6 RMSE (ERMS)and correlation coefficient (R2)of different numbers of hidden layer nodes

由图可知，当隐含层节点数为9 时，误差最小，相关系数最大，预测效果最好，因此，本模型隐含层节点数设置为9。

3.3 神经网络隐含层传递函数选择

隐含层的传递函数同样对模型的预测性能有较大的影响[30]。采用3 种传递函数(Purelin、Tansig 和Logsig)，建立相对应的神经网络预测模型进行测试，并计算了R2和ERMS，其结果见表2。

表2 不同传递函数预测结果Table 2 Prediction results of different transfer functions

由表2 可知，当隐含层传递函数为“Tansig”时，模型整体预测效果最好。另外，本文将Adaboost 算法中的弱学习器设置为10 个，遗传算法个体数目和最大遗传代数分别设置为20 和50，交叉概率和变异概率分别为0.7 和0.01。

4 模型结果及对比分析

4.1 模型预测结果

利用相应的数据对预测模型进行训练和测试，其结果如图7 所示。由图可知，无论是训练结果还是测试结果，大部分数据的预测值接近实际值，说明预测效果较好，可以对储层裂缝进行较为精准地预测。另外，由于神经网络模型的权值和阈值是随机取值，然后由训练数据进行训练调整，因此极易产生过拟合现象，造成训练集的误差小而测试集的误差大，而Adaboost-GA-BP 预测模型的训练集和测试集的预测结果大体相同，说明神经网络预测模型经过优化后没有陷入过拟合现象，具有较高的泛化能力，适应性强。

图7 Adaboost-GA-BP 预测模型结果Fig.7 Prediction results of Adaboost-GA-BP prediction model

4.2 不同预测模型的对比分析

为了验证Adaboost-GA-BP 神经网络预测模型的预测效果，建立了其他4 种预测模型并利用相同的数据进行训练和预测进行对比分析，计算了预测结果的误差和相关系数(图8、表3)。

表3 不同预测模型的预测误差及相关系数Table 3 Prediction error and correlation coefficient of different prediction models

图8 不同预测模型的预测结果Fig.8 Prediction results of different prediction models

由图及表可知，与神经网络预测模型相比，极限学习机和随机森林预测结果误差较大，其中极限学习机预测误差最大。与BP 和GA-BP 神经网络预测模型相比，Adaboost-GA-BP 预测模型的预测结果误差最小，最接近实际值，表明Adaboost-GA-BP 模型具有最高的预测精度。这些模型的预测精度从低到高依次为：极限学习机，随机森林，BP 神经网络，GA-BP 神经网络，Adaboost-GA-BP 神经网络。在构建Adaboost-GABP 模型的过程中，遗传算法可以优化BP 神经网络的权值和阈值，从而提高BP 神经网络的预测精度。Adaboost 算法可以根据训练样本的训练误差及时调整训练样本的权重，使预测精度高的弱预测器的权重变得更高，使得预测模型的预测精度和泛化能力都得到了很大的提高[31]。

5 结论

a.针对储层裂缝宽度的预测问题，建立了Adaboost-GA-BP 预测模型，并利用现场实际数据对其进行了训练和测试。结果表明，建立的Adaboost-GA-BP 预测模型的均方根误差为18%，相关系数为0.98，优于其他模型，可对储层裂缝宽度进行更为精准的预测，为堵漏方案的制定提供一定的指导。

b.通过相关性分析，对储层裂缝宽度的相关因素进行了计算分析和排序，并筛选了模型输入参数。另外，利用附加动量算法和变学习率算法对模型收敛速度进行了提升，使其训练数据绝对误差和降低了27%，同时优选了模型结构。最后，通过Adaboost 算法和GA算法对BP 神经网络进行优化，克服了其收敛速度慢、易陷入局部极小值的缺点，提升了模型的预测性能。

c.由于数据量有限，本研究建立的预测模型仅针对某一区块进行了验证，未来将收集更多区块数据对模型进行训练及验证，提升其适应能力。