高速直升机共轴刚性旋翼悬停气动特性的参数影响研究
胡志远,史勇杰,徐国华,温小军
南京航空航天大学 直升机动力学全国重点实验室,江苏 南京 210016
高速直升机共轴刚性旋翼由两副尺寸相同、旋转方向相反的旋翼构成,它没有常规直升机的结构复杂的挥舞铰和摆振铰,并充分利用了高速前飞时旋翼前行桨叶动压大的特点,使前行桨叶承担绝大部分升力[1];另外,通过减小后行桨叶迎角,对桨盘后行侧进行卸载,使后行桨叶产生小升力或几乎不产生升力,从而推迟或避免了后行桨叶产生动态失速的现象[2]。与常规旋翼相比,共轴刚性旋翼上下旋翼前行侧桨叶所产生的升力左右对称,消除了由于单旋翼气流不对称引起的旋翼倾侧力矩。同时,由于上下旋翼旋转方向相反、扭矩相互抵消,可省去用于平衡反扭矩的尾桨装置,提高了功率利用效率。与传统单旋翼直升机相比,在产生相同拉力时,共轴刚性旋翼高速直升机所需要的旋翼直径更小。共轴刚性旋翼兼顾悬停和高速飞行能力,具有结构紧凑、气动效率高、机动性能和操纵性能好等优点。正是这些优点,使得共轴刚性旋翼复合式高速直升机成为当前的研究热点,也代表了未来高速直升机的一个重要发展方向[3]。除了最早提出共轴刚性旋翼的美国西科斯基公司在其研制的X2及改进型S-97 高速直升机中均采用共轴刚性旋翼外,俄罗斯的K-92高速直升机方案中也使用了共轴刚性旋翼[4]。
与常规旋翼相比,共轴刚性旋翼的气动特性要复杂得多。这是由以下几个方面引起的:(1)共轴刚性旋翼由旋转方向相反的两副旋翼构成,这使得即便在悬停状态下,其流场也是非定常的,需要考虑其中的配平影响[5];(2)由于上下旋翼之间存在严重的气动干扰,特别是在悬停状态下,下旋翼大部分区域处于上旋翼的下洗流和尾迹之中,其流场存在涡—涡干扰、桨—涡干扰等复杂流动现象[6-7]。
本文开展了共轴刚性旋翼悬停状态下的气动特性研究。为了真实地反映桨叶的实际运动,需要对共轴刚性旋翼进行配平计算。但与单旋翼流场数值模拟不同的是,共轴刚性旋翼的双旋翼会给配平计算带来很大的困难。为此,本文采用了一个适合于悬停状态共轴刚性双旋翼的计算流体力学(CFD)配平模型。
1 共轴刚性旋翼悬停气动特性计算模型
1.1 CFD求解方法
在惯性坐标系下三维非定常可压Navier-Stokes 方程可表示为[8]
其中

针对共轴刚性旋翼,为了更好地捕捉其中的复杂流动现象和气动干扰效应,本文采用迎风Roe格式[9]对无黏量进行空间离散,同时使用了二阶MUSCL 格式对网格单元内流场进行重构。为处理共轴上下旋翼间的相互干扰作用,将悬停状态按非定常流场进行模拟,并采用双时间步方法进行时间推进,同时在伪时间上使用LU-SGS 时间离散格式来加速计算收敛速度。再考虑到共轴刚性旋翼桨叶表面边界层流动的黏性影响及分离流动现象,本文计算中湍流模型选用Spalart-Allmaras(S-A)模型[10]。
1.2 运动嵌套网格系统
本文将常用的单旋翼嵌套网格生成方法推广到共轴刚性(双)旋翼[3]。共轴刚性旋翼在上下旋翼做旋转运动的同时还存在桨叶变距运动,运动规律较为复杂。为了准确地描述共轴刚性旋翼流场模拟中上下旋翼桨叶复杂的运动规律,这里基于结构运动嵌套网格技术并结合参考文献[4]给出的桨叶三维结构网格生成方法,生成共轴刚性旋翼结构运动嵌套网格系统,主要包括[4]:(1)围绕共轴刚性旋翼桨叶的C-O拓扑型结构网格,该网格与桨叶固连在一起且跟随桨叶一起做旋转运动,用于模拟桨叶附近流场和捕捉近场涡尾迹;(2)包含共轴刚性旋翼桨叶贴体网格的笛卡儿背景网格,用于模拟共轴刚性旋翼空间流场、上下旋翼间干扰及远场尾迹。为了能够更为准确地捕捉桨尖涡和上下旋翼之间的干扰效应[11],在背景网格中对桨尖涡形成区域和上下旋翼之间进行了加密。
需要指出的是,共轴刚性旋翼上下旋翼之间的间距较小,生成共轴刚性(双)旋翼嵌套网格与生成单旋翼嵌套网格有一定的区别,且更为困难:一是上下旋翼之间存在严重的气动干扰,为了捕捉这种干扰效应,需要对上下旋翼之间的背景网格进行加密;二是上下旋翼桨叶的贴体网格不能与对方桨叶实体发生重叠,这就要求桨叶贴体网格边界足够小。同时,模拟中流场域外边界设置为Riemann 远场边界,桨叶物面为无滑移边界,并将桨叶网格外边界作为嵌套插值边界。
1.3 悬停配平分析
共轴刚性旋翼在悬停状态时,上下旋翼桨叶存在变总距的运动。为了真实地反映桨叶的实际运动,使得旋翼总拉力系数达到给定的目标值,同时上下旋翼满足扭矩平衡,需要对悬停状态共轴刚性旋翼进行CFD 配平计算。如果直接采用CFD 进行配平,会导致计算量急剧增加,这在科学研究和工程实用中都是不现实的。因此,采用了本文建立的适用于悬停状态共轴刚性旋翼的CFD 配平计算的方法[4]。由于共轴刚性旋翼的气动特性参数与总距之间为非线性变化关系[12-13],本文通过Newton-Rhapson迭代方法求解旋翼操纵量。
1.4 计算方法的算例验证
图1 和图2 分别是计算的Caradonna-Tung 旋翼[14]在θ0.75=8°、Matip=0.877状态下桨叶剖面压力分布图和桨叶剖面拉力系数沿展向分布图,由图1 和图2 可知,本文计算结果与参考文献[14]的试验值吻合得比较好。
图3给出了UH-60A模型旋翼悬停性能计算结果与试验值[15]的对比。由图3 可知,虽然旋翼性能的计算是富有挑战性的,但本文计算结果与参考文献试验值仍吻合良好,这表明本文建立的数值方法适用于计算具有复杂气动外形的旋翼悬停气动性能。
2 计算结果与分析
悬停状态下的单旋翼可认为是定常的,其拉力基本不随方位角变化,而共轴刚性旋翼由于其上下旋翼间的相互干扰,具有严重的非定常特性。不同于常规单旋翼悬停流场的定常特征,共轴刚性旋翼由于其上下旋翼旋转方向相反,即使在悬停状态下其流场也是非定常的。在悬停状态下,共轴刚性旋翼上下旋翼之间存在严重的气动干扰。除了旋翼桨叶与自身尾迹的干扰外,上旋翼桨叶与下旋翼桨叶、桨叶与另一旋翼尾迹之间、上下旋翼尾迹之间都会出现干扰。
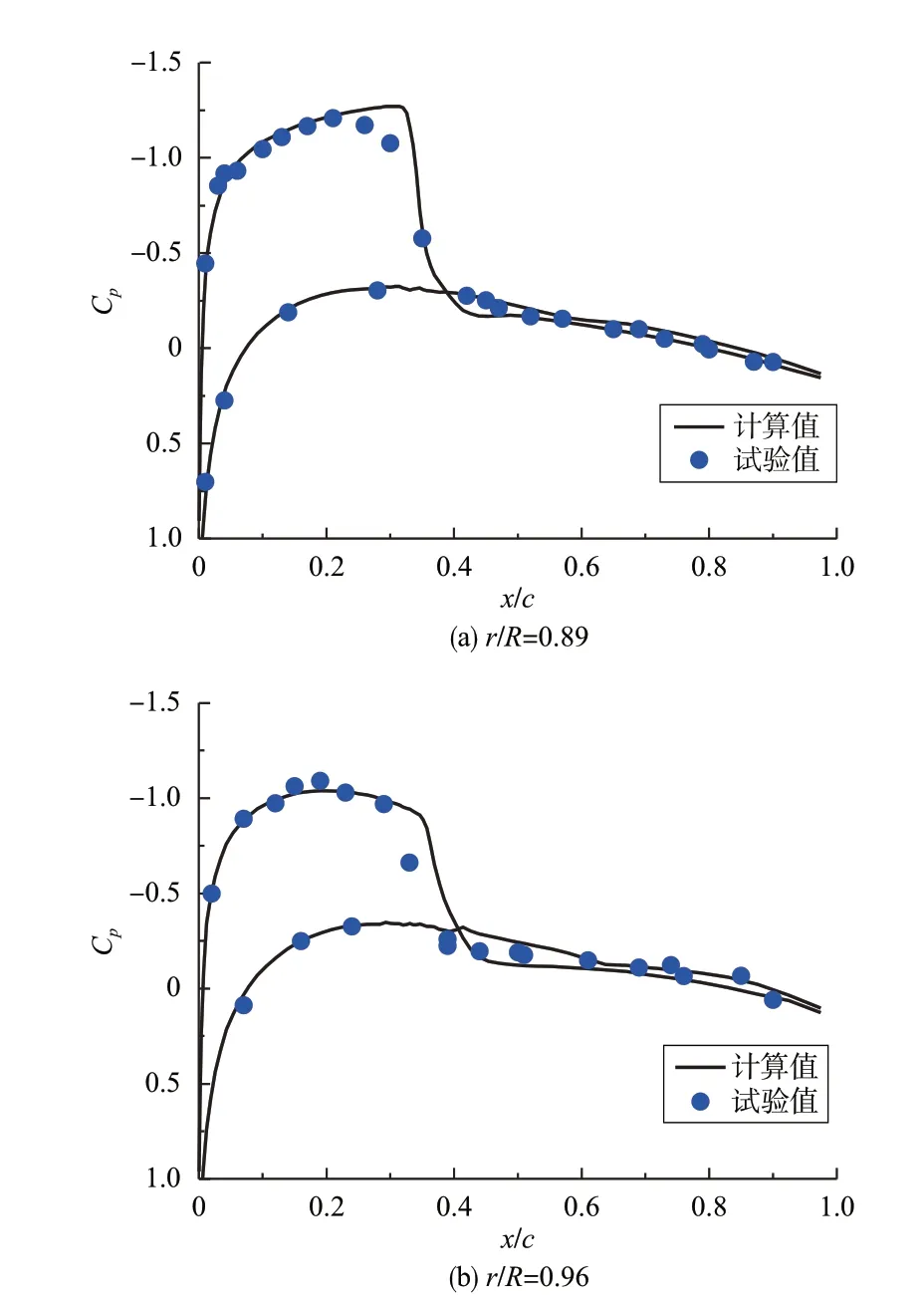
图1 Caradonna-Tung旋翼在θ0.75=8°, Matip=0.877计算状态下的桨叶剖面压力分布Fig.1 The pressure distribution on the blade cross-section of the Caradona-Tung rotor in the state of θ0.75=8°, Matip=0.877
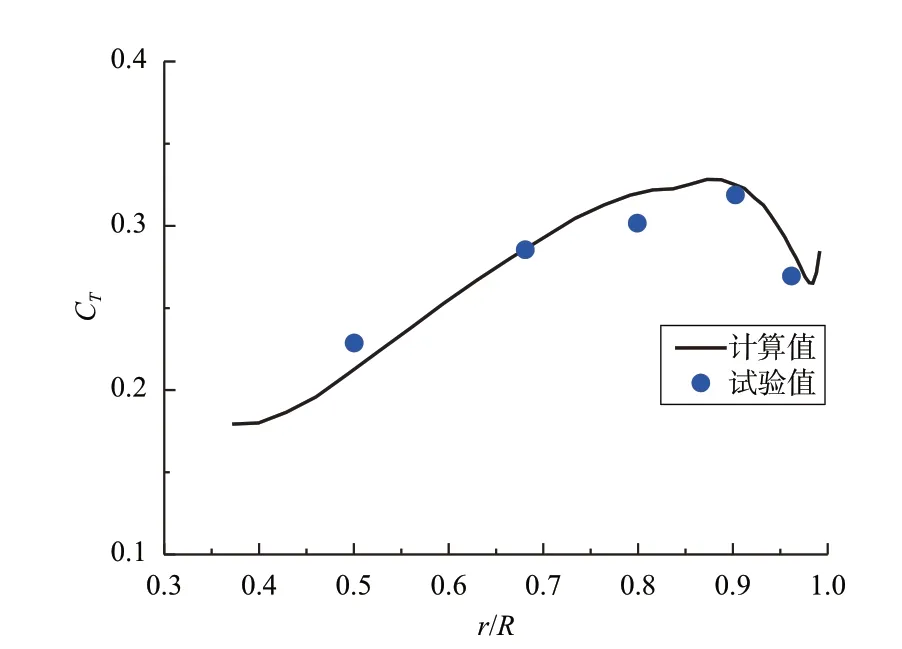
图2 Caradonna-Tung旋翼在θ0.75=8°, Matip=0.877状态下的桨叶剖面拉力系数沿展向分布Fig.2 The thrust coefficient distribution on the blade cross-section of the Caradona-Tung rotor in the state of θ0.75=8°, Matip=0.877

图3 UH-60A模型旋翼悬停性能计算结果与试验值的对比Fig.3 The comparison between the calculated results and experiment for hovering performance of the UH-60A model rotor
共轴刚性旋翼的上下旋翼轴向间距比较小,因而其干扰影响会比常规共轴双旋翼更大。以美国高速直升机的验证机XH-59 为例,它的轴向间距约为0.14R,而俄罗斯Ka-28 直升机的常规共轴双旋翼轴向间距达到了0.2R以上[4]。这里重在研究共轴刚性旋翼的气动特性,对于旋翼结构和桨叶形状的细节(如桨叶根部连接方式、特殊平面形状等)不十分关注,因此算例中采用Harrington rotor-2 旋翼[11]为计算模型,其轴向间距为0.16R,符合共轴刚性旋翼的特征。本文的算例都采用了同一尺度的网格系统,背景网格尺度为143×168×143,网格单元数为3435432 个;桨叶贴体网格使用C-O形网格,网格尺度为177×49×74,单片桨叶网格单元数为641802个。
2.1 悬停气动性能
为了研究上下旋翼间距对共轴刚性旋翼悬停气动特性的影响,计算了目标拉力系数CT=0.005时、旋翼间距为1.0h(0.16R)和1.5h(0.24R)时共轴刚性旋翼的气动性能。当间距为1.0h时,旋翼处于配平状态,目标拉力系数CT=0.005;当间距为1.5h时,保持上下旋翼总距与间距为1.0h时相同,故该间距时旋翼不处于配平状态。
图4给出了不同旋翼间距时上下旋翼拉力系数和扭矩系数随方位角的变化曲线。从图4 中可以看出,随着旋翼间距增加,最大脉冲幅值减小。随着旋翼间距增加,上旋翼拉力变大,而下旋翼拉力减小。对于上旋翼,旋翼间距增加后,上旋翼诱导入流受下旋翼“吸引”作用减弱,增大了其有效迎角,表现为上旋翼拉力变大;而对于下旋翼,当旋翼间距增加后,上旋翼在下旋翼桨盘位置处的下洗速度增大,减小了下旋翼的有效迎角,表现为下旋翼拉力变小。同理,上旋翼扭矩随旋翼间距增大而增加,下旋翼扭矩随旋翼间距增加而减小。不管是拉力还是扭矩的脉冲幅值都随旋翼间距增大而减小,这也说明旋翼间距增加后,上下旋翼之间的干扰作用减弱。
2.2 桨叶气动外形参数对悬停气动特性的影响
共轴刚性旋翼高速直升机最显著的特点就是采用了共轴刚性旋翼来实现高速飞行,而共轴刚性旋翼气动特性与其桨叶气动外形设计密切相关。因此,本节拟应用上节建立的适合于共轴刚性旋翼的流场数值模拟方法,开展桨叶气动外形设计参数对共轴刚性旋翼气动特性影响的研究。为了便于后面的计算对比与分析,这里定义了几种共轴刚性旋翼桨叶气动外形。
在本节算例中,主要开展共轴刚性旋翼桨叶翼型配置、扭转分布对悬停气动特性的影响研究,其计算状态为:桨尖马赫数Matip= 0.5544、拉力系数CT为0.002~0.008。
2.2.1 基准旋翼参数
表1给出了基准旋翼参数,其旋翼实度与X2高速直升机(σ=0.1441)相近。为了便于对比分析,后文其他气动外形桨叶都以此旋翼桨叶为基准,分别进行翼型配置、扭转分布更改而给出,并保持其他旋翼桨叶参数一致。后文基准桨叶即指该基准旋翼桨叶。
2.2.2 翼型配置方案
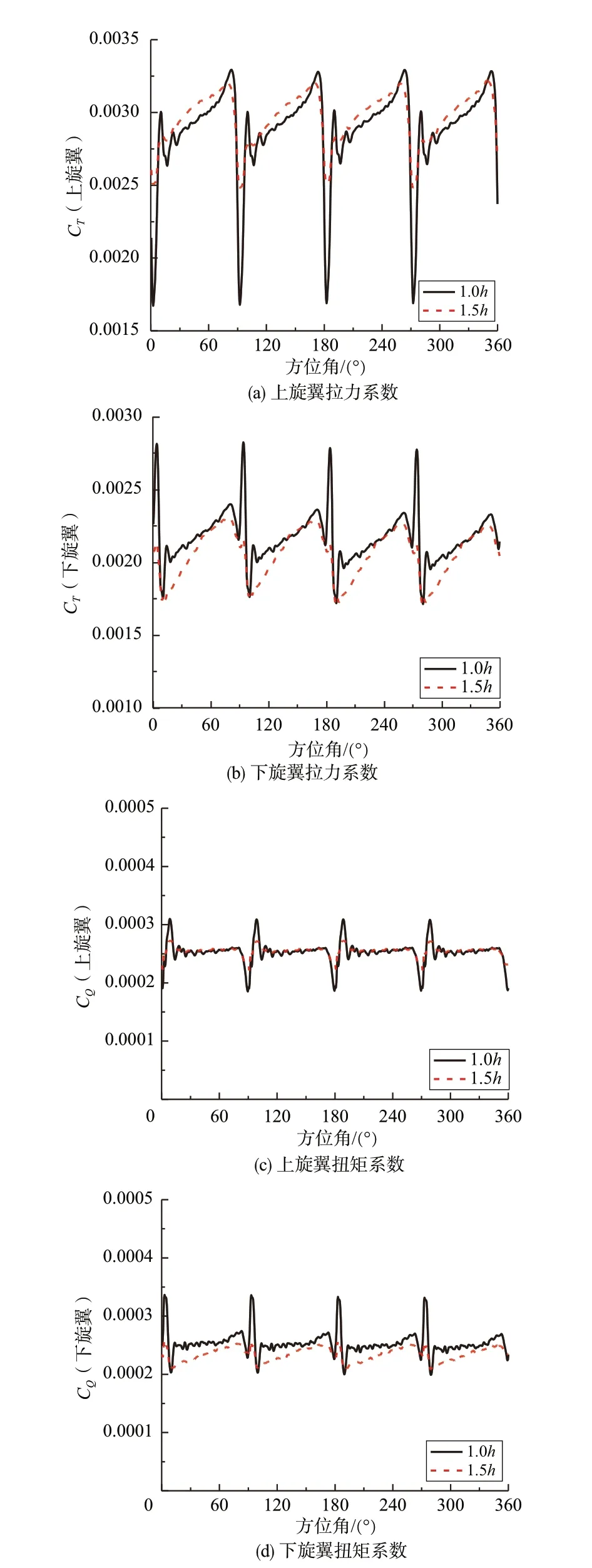
图4 不同旋翼间距时拉力和扭矩系数随方位角的变化曲线(CT=0.005)Fig.4 The variation of thrust and torque coefficients of azimuth angle for different rotor spacing(CT=0.005)
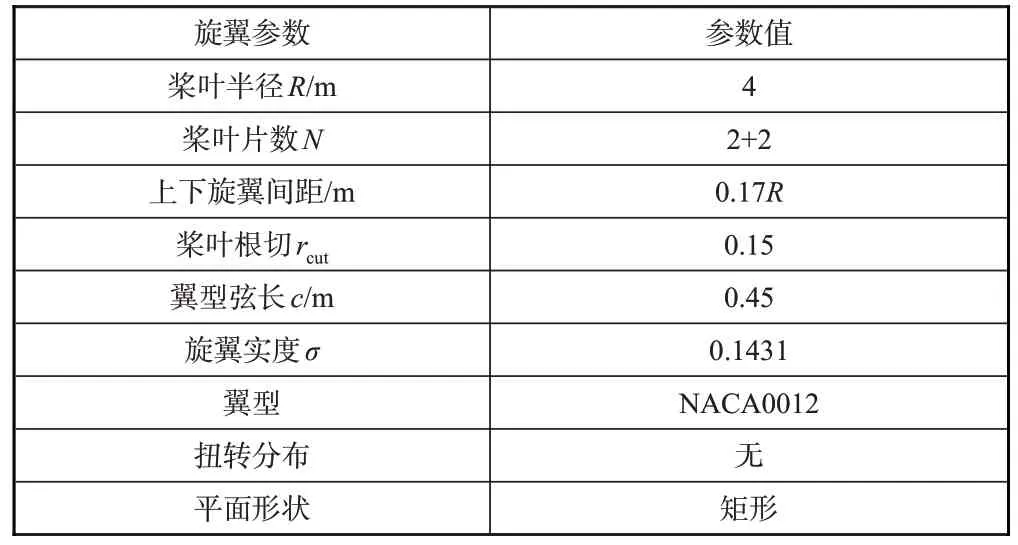
表1 基准旋翼参数Table 1 The reference rotor parameters
针对共轴刚性旋翼在高速前飞时,后行桨叶内侧会出现反流区,选择反流气动特性较好的双钝头翼型[16]对基准旋翼桨叶进行更改设计,给出共轴刚性旋翼桨叶“翼型配置1”方案。在该方案中,用双钝头翼型替换基准旋翼桨叶0.15R~0.35R段的NACA0012 翼型。为了增大共轴刚性旋翼的拉力,选用升力特性较好的OA209 翼型替换“翼型配置1”方案中0.4R~0.8R段的NACA0012 翼型,同时,针对高速前飞时前行桨叶桨尖部分容易出现激波的现象,采用薄翼型OA206 替换“翼型配置1”方案中0.85R~R段的NACA0012 翼型,形成共轴刚性旋翼桨叶“翼型配置2”方案。
表2给出了用于共轴刚性旋翼桨叶翼型配置对气动特性的影响研究的两种方案。
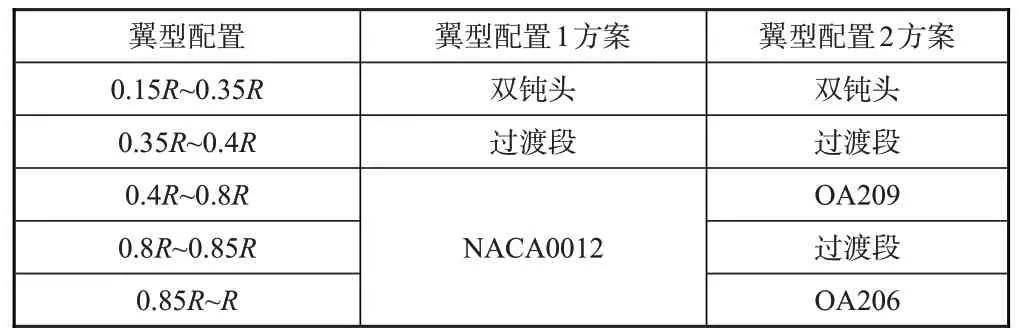
表2 翼型配置方案Table 2 The airfoil configuration scheme
2.2.3 桨叶扭转分布
首先,为了提高共轴刚性旋翼的悬停效率,依据常规单旋翼传统桨叶扭转设计方法,对基准旋翼桨叶采用线性负扭转设计,给出了共轴刚性旋翼桨叶“负扭转”方案。其次,为了减小共轴刚性旋翼桨叶根部的安装角,使反流与后行桨叶的相对迎角变小,从而减小高速前飞时后行桨叶根部的负升力和阻力,对基准旋翼桨叶采用正负扭转设计,即桨叶内段采用线性正扭转设计,桨叶外段采用线性负扭转设计,给出了共轴刚性旋翼桨叶“正负扭转”方案。
表3给出了用于共轴刚性旋翼桨叶扭转分布对气动特性的影响研究的两种方案。
2.2.4 翼型配置的影响
图5给出了不同翼型配置方案对应的上下旋翼配平总距随总拉力的变化曲线。从图5中可以看出:(1)在相同的共轴刚性旋翼拉力系数时,“翼型配置2”方案中的上旋翼和下旋翼需要的总距与基准桨叶和“翼型配置1”方案相比都要小,这是因为“翼型配置2”方案中采用了升力特性较好的OA209 和OA206翼型替换“翼型配置1”方案中的NACA0012翼型;(2)在相同的共轴刚性旋翼拉力系数时,“翼型配置1”方案中的上旋翼和下旋翼需要的总距与基准桨叶基本相等,这是因为,虽然利用了双钝头翼型替换基准桨叶桨根部分的NACA0012翼型,但是在悬停状态下,旋翼拉力主要由桨叶外侧产生,桨叶内侧尤其是桨根部分产生的升力较小。
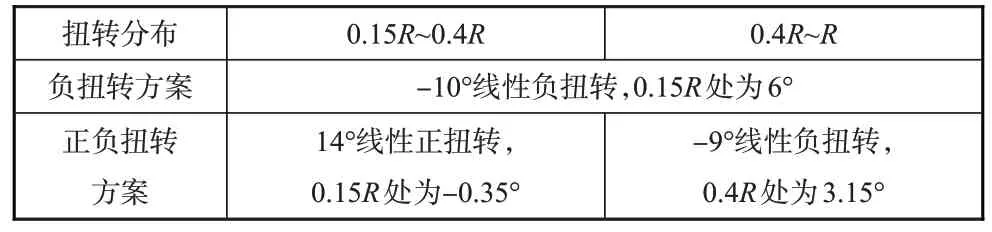
表3 扭转分布方案Table 3 The twisted distribution scheme
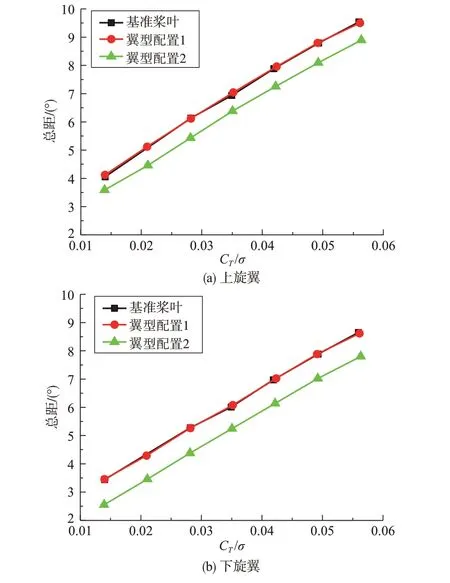
图5 不同翼型配置方案中的上下旋翼配平总距随总拉力系数的变化Fig.5 The variation of trim values of the upper and lower rotors with the total thrust coefficient in different airfoil configuration schemes
图6 和图7 分别给出了不同翼型配置方案对应的共轴刚性旋翼扭转系数、悬停效率随总拉力系数的变化曲线。共轴刚性旋翼悬停效率定义为[4,17]:FM=C/(CQco),其中,总拉力CTco=CTu+CTL、总扭矩CQco=CQu+CQL分别为上下旋翼拉力、扭矩之和。从图6 中可以看出:(1)在相同的总拉力系数下,“翼型配置1”方案对应的扭矩系数最大,这是因为气流由桨叶翼型前缘吹向后缘时,双钝头翼型的升阻特性不如传统尖后缘翼型(NACA0012),从而导致“翼型配置1”方案桨叶内段升力减小,阻力增大;(2)在相同的总拉力系数下,“翼型配置2”方案对应的扭矩系数最小,这是因为OA209和OA206的升阻特性比NACA0012翼型好,它们可以增大旋翼的升力并减小阻力。从图7中可以明显看出,基准桨叶的悬停效率优于“翼型配置1”,“翼型配置2”的悬停效率最高。
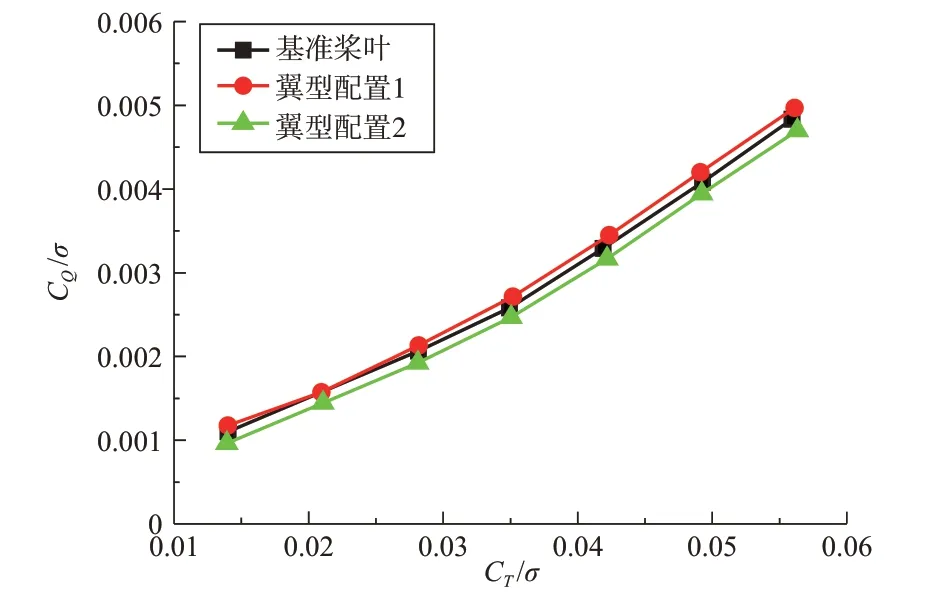
图6 不同翼型配置方案的共轴刚性旋翼扭转系数随总拉力系数的变化Fig.6 The variation of torque coefficient with total thrust coefficient for different airfoil configuration schemes
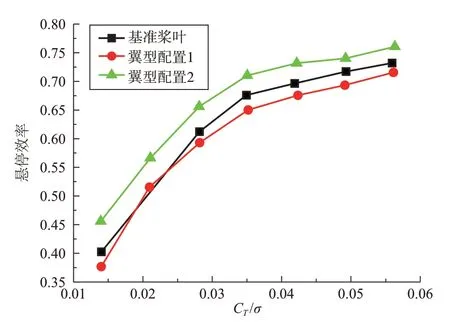
图7 不同翼型配置方案的共轴刚性旋翼悬停效率(FM)随总拉力系数的变化对比Fig.7 The variation of FM with total thrust coefficient for different airfoil configuration schemes
图8给出了目标拉力系数为CT=0.008时不同翼型配置方案拉力系数和扭矩系数随方位角的变化曲线。由图8可知,拉力系数与扭矩系数变化曲线都具有周期性;三种翼型配置的拉力系数曲线稍有误差,但还是基本接近,这是因为本文悬停配平计算设置与目标拉力系数误差达到1%以内时计算收敛,如果配平精度设置提高,计算误差将减小,但耗费的计算时间也将大大增加。另外,由图8 中可知,“翼型配置1”方案的扭矩系数最大,而“翼型配置2”方案的扭矩系数最小,这与前文获得的结果是一致的。
据以上分析可以得出:双钝头翼型会降低共轴刚性旋翼悬停效率,采用升阻特性好的翼型可以提高共轴刚性旋翼的悬停效率。
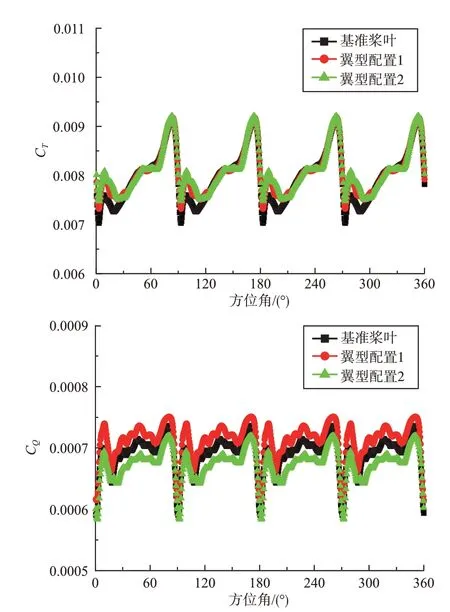
图8 不同翼型配置方案的拉力系数与扭矩系数随方位角的变化(CT=0.008)Fig.8 The variation of thrust coefficient and torque coefficient with azimuth angle for different airfoil configuration schemes (CT=0.008)
2.2.5 扭转分布的影响
图9给出了不同扭转分布方案对应的上下旋翼配平总距随总拉力的变化曲线。由图9可知:(1)在相同的共轴刚性旋翼拉力系数时,“负扭转”方案对应的上旋翼和下旋翼配平总距比基准桨叶小,且在大拉力系数时小得更多,这只是因为“负扭转”方案增大了桨叶大部分剖面安装角,从而增大了剖面迎角;(2)在相同的共轴刚性旋翼拉力系数时,“负扭转”方案对应的上旋翼和下旋翼配平总距小于“正负扭转”方案的值,这是因为“正负扭转”方案减小了桨叶内侧的安装角,使得桨叶内侧剖面迎角减小。
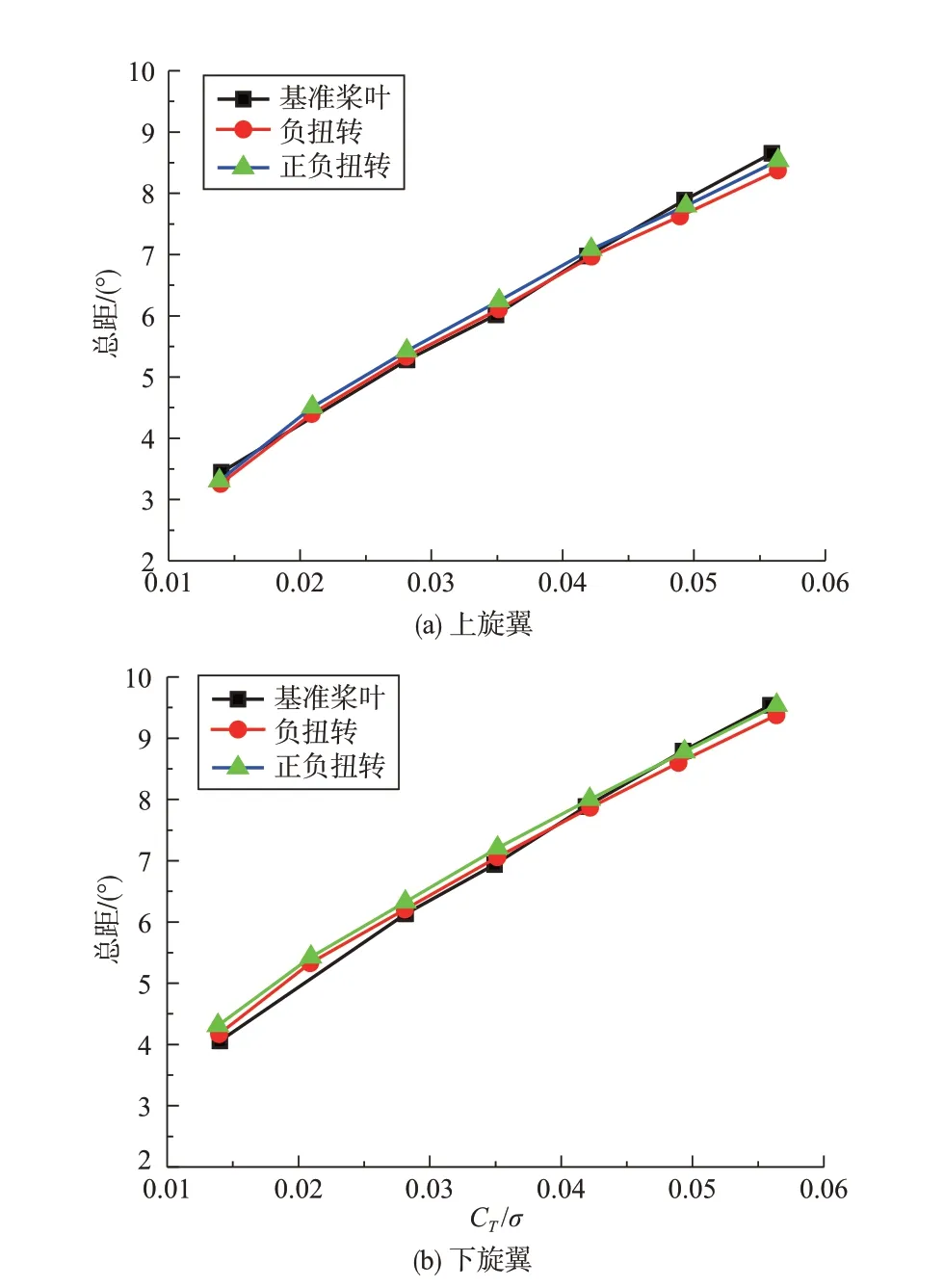
图9 不同扭转分布方案的上下旋翼配平总距随总拉力系数的变化Fig.9 The variation of trim values of the upper and lower rotors with the total thrust coefficient in different torsion distribution
图10 和图11 分别是不同扭转分布方案对应的共轴刚性旋翼扭转系数和悬停效率与总拉力系数的关系曲线。从图10和图11中可以看出:(1)在相同的总拉力系数下,基准桨叶的扭矩系数比“负扭转”方案的要大,且悬停效率更低。随着拉力增加,两者的扭矩系数和悬停效率相差更大,这是因为负扭转使得旋翼桨叶的诱导速度分布更均匀一些,从而减小诱导功率,提高悬停效率,并且在大载荷时更为明显;(2)在相同的总拉力系数下,“负扭转”方案对应的扭矩系数比“正负扭转”方案的要小,悬停效率更大,且随着拉力的增加,两者扭矩系数和悬停效率相差更大,这是因为“正负扭转”方案使旋翼桨叶诱导速度沿展向分布更不均匀,增大了诱导功率。
图12 计算了目标拉力系数CT=0.008 时不同扭转分布方案对应的拉力系数和扭矩系数随方位角的变化曲线。由图12 可知,拉力系数和扭矩系数变化曲线都具有周期性,且拉力系数变化曲线基本重合,在各方位角处,基准桨叶的扭矩系数最大,而“负扭转”方案的扭矩系数最小。
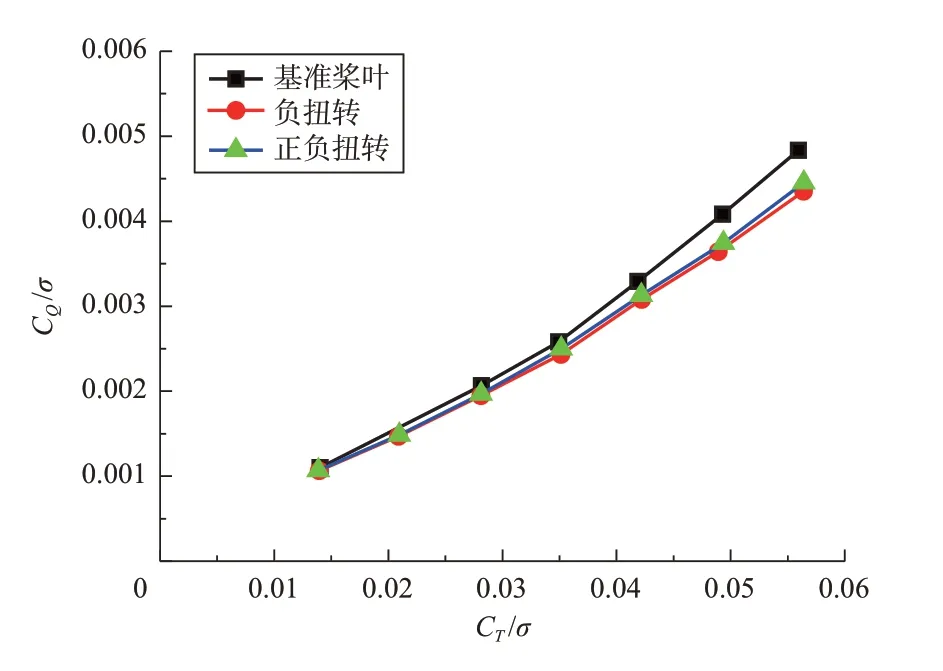
图10 不同扭转分布方案的共轴刚性旋翼扭转系数随总拉力系数的变化Fig.10 The variation of torque coefficient with total thrust coefficient for different torsion schemes
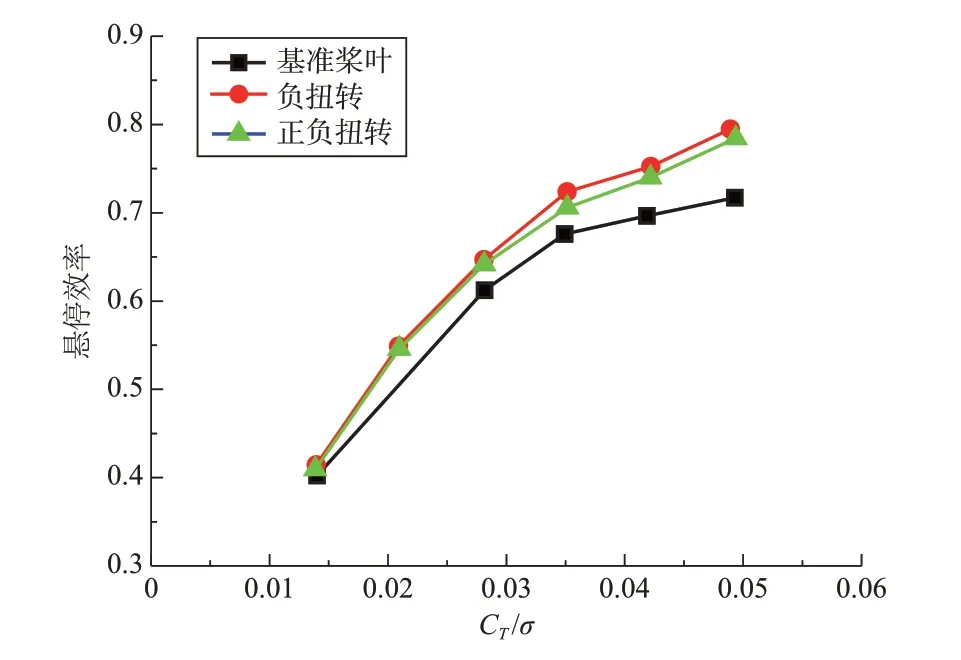
图11 不同扭转分布方案的共轴刚性旋翼悬停效率(FM)随总拉力系数的变化Fig.11 The variation of FM with total thrust coefficient for different torsion schemes
根据以上分析可以得出:与无扭转分布相比,负扭转可以提高共轴刚性旋翼的悬停效率;与负扭转分布相比,桨叶内侧采用正扭转分布会降低共轴刚性旋翼的悬停效率。
3 结论
本文进行了共轴刚性旋翼悬停状态下的气动特性计算,着重开展了桨叶气动外形设计参数和上下旋翼间距对共轴刚性旋翼悬停气动特性影响的研究,得到以下结论:
(1) 算例计算结果表明,本文建立的计入配平分析的悬停气动特性计算方法适用于共轴刚性旋翼气动性能的计算与分析。
(2) 计算表明,双钝头翼型会降低共轴刚性旋翼的悬停效率,因而共轴刚性旋翼宜在桨叶内侧采用双钝头翼型。
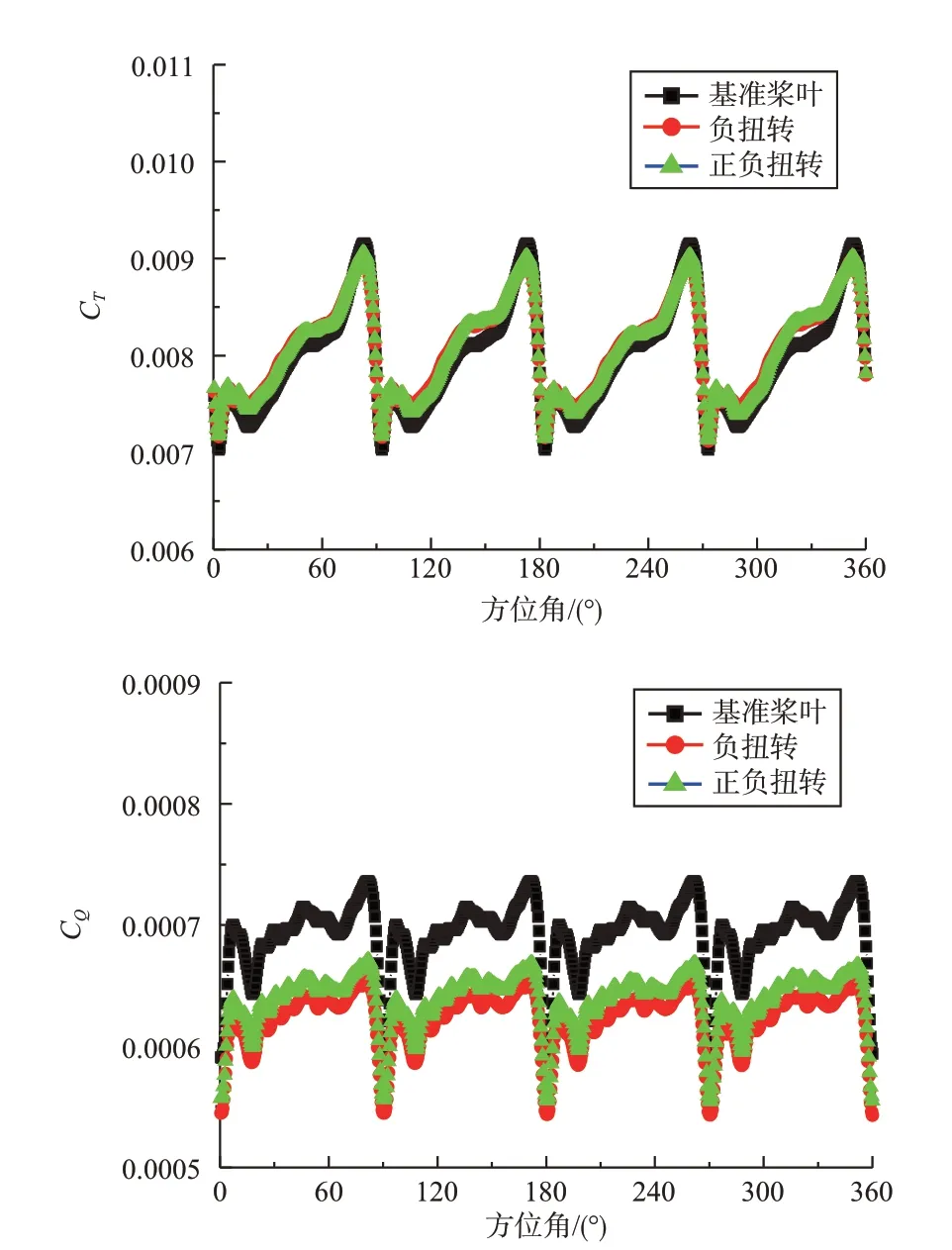
图12 不同扭转分布方案的拉力系数与扭矩系数随方位角的变化曲线(CT=0.008)Fig.12 The variation of thrust coefficient and torque coefficient with azimuth angle for different torsion schemes (CT=0.008)
(3) 在升力分布占主导的桨叶外侧采用升阻特性好的翼型可以提高共轴刚性旋翼的悬停效率。
(4) 负扭转可以提高共轴刚性旋翼的悬停效率,但采用正扭转分布,与负扭转分布相比,会降低共轴刚性旋翼的悬停效率。在进行共轴刚性旋翼设计时,桨叶内侧应采用正扭转分布,而在外侧应采用负扭转分布。
(5) 对于本文算例,保持拉力系数相同,桨叶采用“翼型配置2”方案时,其悬停效率较基准桨叶最大可提高3.2%。

