基于改进向量场直方图算法的无人机动态避障策略
符小卫,吴迪,支辰元
西北工业大学,陕西 西安 710072
随着战场环境日益复杂多变,微型旋翼无人机凭借其造价低廉、机动性好、难以拦截等优点,在侦察监视、电子战攻击等领域能够极大提高任务完成效率[1]。
为了让无人机能够在复杂未知环境下,自主高效完成任务,国内外专家学者对无人机路径规划算法进行了深入研究,主要涉及全局规划算法和局部规划算法两类。人工势场法于20世纪80年代由Khatib提出, 将移动机器人的运动视作质点在一种抽象的人造势力场中的运动:目标点对质点产生引力, 而障碍物对质点产生斥力, 依据合力确定移动机器人的运动方向和路径[2-3]。尼尔森等在1980 年提出了A*算法, 是一种应用很广的启发式搜索算法。利用空间启发式信息, 通过对比选择恰当的评估函数, 通过动态搜索策略, 求出移动机器人的最优规划路径。刘斌和许震洪等[4-5]提出了一种基于A*算法的动态多路径规划方法,结合A*算法与矩形限制搜索区域算法, 给出了一种求解单一优化路径的动态路径规划算法,同时提出了一种重复路径惩罚因子, 利用一次搜索得出多条优化路径。彭锦城等[6]提出了基于改进Hybrid A*的无人机路径规划算法,通过改进Hybrid A*前端三维路径搜索的启发式函数和后端非线性优化的平滑函数,解决了无人机自主避障飞行中快速旋转翻转等问题,提高了无人机目标识别、侦察监视的准确度。
针对传统VFH算法[7-13]的无记忆性而易于陷入局部陷阱且阈值选择影响避障性能优劣,本文提出一种实时陷阱检测机制,在激光雷达[10]探测信息的基础上动态添加历史栅格信息以避免陷入局部陷阱,并设计了一种动态阈值更新策略,克服了传统VFH 算法的阈值敏感性问题,增强了算法在不同场景的泛化性。由于在障碍物信息不确定环境下单无人机避障规划问题中,传统的全局规划算法(如A*算法)需要完全了解全局环境且无法满足实时性要求,本文基于局部规划和全局规划的特点,将A*算法与改进的VFH算法相结合[11],设计了一种复杂环境中的单无人机路径规划与避障策略,在静态已知障碍物的全局路径规划基础上,根据激光雷达采集的数据辅助无人机局部规划处理,实现有效避障。
1 环境建模
与大多数传统建模方法中的假定障碍物分布情况全局已知不同,本文研究不确定的障碍物分布情况,即无人机在飞行前对地形信息并非完全了解,需要在飞行过程中实时探测周围的地形情况[14-15]。本文的研究场景如图1所示,在l×l的二维空间区域内包括静态已知障碍物与未知障碍物:图1 中深蓝色几何体为静态已知障碍物,代表通过情报、地图或其他手段获取到的地形信息,无人机在起飞前就对这些障碍物完全了解,因此可以通过这些信息进行初步的路径规划;图1中浅蓝色几何体为未知障碍物,其坐标位置、大小、形状都是未知的,无人机需要运动到其四周才能探测到其信息。
本文假设一架微型四旋翼无人机始终在同一高度平面内运动,并建立二维空间内的无人机二阶运动模型。
式中,在t时刻时,无人机的位置矢量为pu(t) =(pux,puy),速度矢量为v(t) =(vx,vy),加速度矢量为u(t) =(ux,uy),加速度矢量为无人机的控制输入量。四旋翼无人机具有最大速度限制,|v(t)| ≤vmax。四旋翼无人机的任务是穿越障碍物区域到达目标位置pg=(pgx,pgy)。
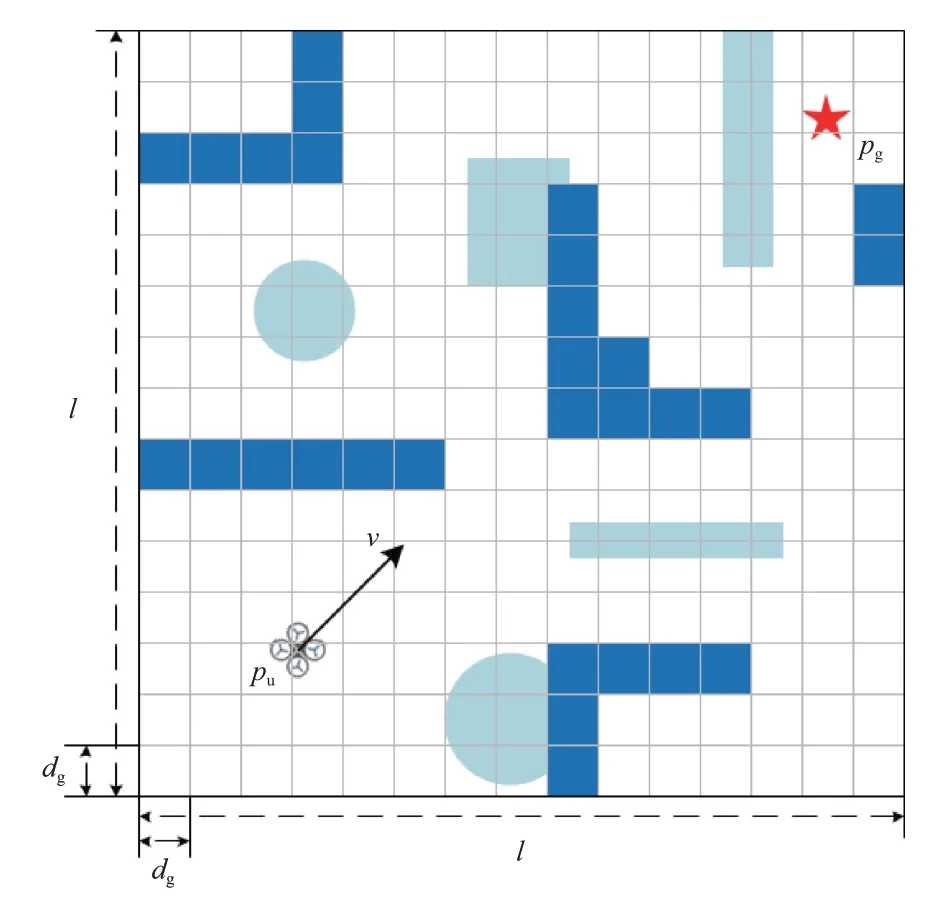
图1 无人机避障场景图Fig.1 UAV obstacle avoidance scene
在使用A*算法进行全局路径规划之前需要对地形进行合理构建,本文采用栅格法对地图进行建模,将无人机所在二维场景划分为大小相同的矩形栅格点,栅格精度为dg。因此,可用一个二维矩阵M=(mij)n×n表示该二维地图信息,其中,矩阵中每个元素表示一个dg×dg的矩形区域内的地形信息。当栅格点属于静态障碍物点集时mij=1,否则mij= 0。
本文采用激光雷达作为传感器来进行地形探测,设其水平分辨律为ar,最大探测距离为dr,即在以激光雷达挂载点为圆心、dr为半径的圆形区域内每隔ar角度收集该方向上的地形信息,其示意图如图2 所示。激光雷达每一帧返回的数据以点云的形式呈现,表示该未知障碍物的轮廓表面的点数据集合。以无人机的时变全局坐标pu(t) =(pux,puy)为中心建立局部时变坐标系Γ 用来表示每个点的坐标。点云中第i个点的时变全局坐标为pi=(pix,piy),即Γ中对应的坐标为piu=(pix-pux,piy-puy)。
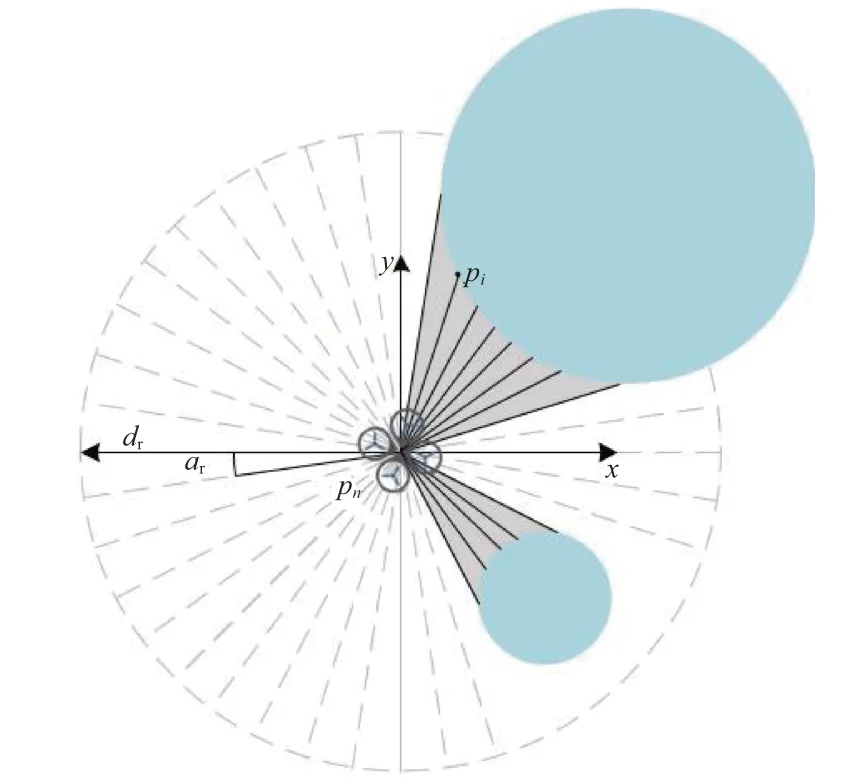
图2 激光雷达点云示意图Fig.2 Lidar point cloud map
2 传统向量场直方图算法原理
向量场直方图(VFH)算法将无人机四周的障碍物映射到了以无人机为中心的极坐标系上,并采用三个层次的数据信息表示方法来对传感器反馈的无人机周边环境信息进行逐级数据缩减,以用于最终的基于阈值的方向控制,具体算法实现如下。
(1) VFH算法的第一步同样需要构建栅格地图。如图3所示,将运行环境以栅格形式进行划分,以无人机为中心构建活动窗口,并通过cij表示栅格内存在障碍物的置信度,该值随着激光雷达的不断扫描而递增更新。
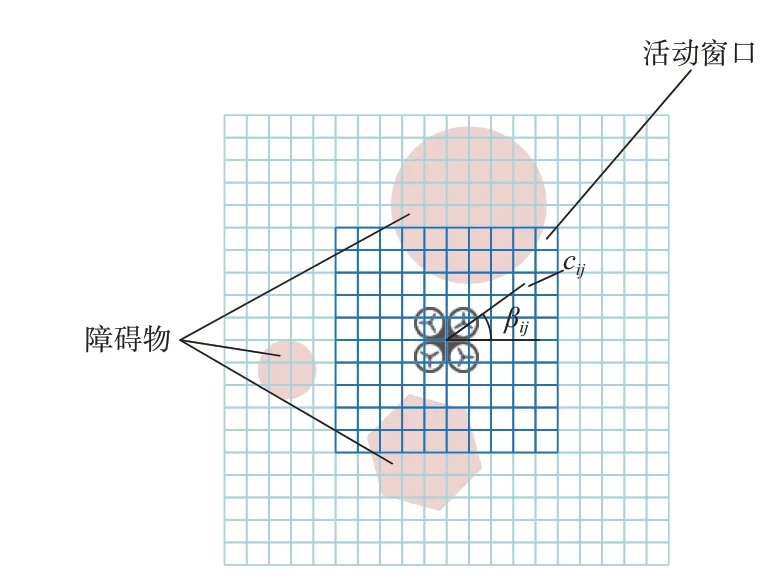
图3 栅格地图构建Fig.3 Grid map construction
(2) 第二层VFH算法将栅格置信度矩阵和相对无人机的距离映射到极坐标直方图上。以无人机坐标pu=(pux,puy)为中心建立极坐标系,每个栅格点(i,j)都可以看作一个由无人机指向栅格点的矢量,βij为该栅格在极坐标系下的角度,mij为障碍物确定度,用于计算极障碍物密度(POD)
式中,点(i,j)的坐标为(xi,yj);cij为该栅格点的障碍物置信度;dij为该栅格点距离无人机的欧氏距离;a、b为正常数,且取值满足a-bdmax=0,其中dmax是无人机当前位置到活动窗口中最远栅格的距离。
在VFH 算法中,无人机采用激光雷达等传感器,具有360°全向视野。水平角度分辨率为ar,表示将360°视野分为n个角度为ar的扇区,即n=。因此,每个栅格点即位于对应的扇区中,其扇区编号k如式(4)所示
式中,k= 0, 1, …,n- 1。每一个扇区,都有一个极障碍物密度值,记作hk,由该扇区角度范围内障碍物确定度计算可得。
(3) 第三层是算法输出,经过第一层及第二层的障碍物信息处理,得到极坐标直方图H,以表示无人机周围各个扇区内的障碍物分布情况。
直方图中存在多个波峰波谷,设置一个阈值T来筛选出可能的前进方向。图4 所示是一个典型的极坐标直方图,其中每一个蓝色柱形即为扇区对应的平滑处理后的极障碍物密度值。图4中红线即阈值T,根据极障碍物密度值小于阈值的扇区为波谷,从直方图中筛选出三个备选波谷。

图4 极坐标直方图Fig.4 Polar coordinate histogram
设定角度阈值at,根据每个波谷跨越的连续扇区角度值大小将波谷划分为宽波谷和窄波谷,若波谷宽度大于at则是宽波谷,否则是窄波谷。定义第m个波谷的起始和终止角度边界值为αm_begin和αm_end,针对每一个波谷计算无人机运动的备选方向。窄波谷的角度中线即为备选方向,即;而宽波谷会在贴近边界处产生两个备选方向,即。
得到所有备选方向后根据目标在局部时变坐标系Γ下角度αg,选择进行前进方向αtarget。若第m个波谷有αm_begin<αg<αm_end,即包含角度αg对应方向,则直接向目标运动即可;否则找出与αg最接近的备选方向作为新的αtarget。如图5 所示,目标方向被波峰遮挡,因此无人机从波谷1 中选择与目标方向最接近的备选方向作为前进方向。
最后根据本文研究场景,通过VFH算法设计无人机控制律,即u=(ηcos(αtarget),ηsin(αtarget)),其中η为正常数。
3 改进的VFH算法
VFH算法作为一种局部路径规划算法,存在以下缺陷:(1)传统VFH算法的无记忆性导致在一些特殊场景中易陷入局部陷阱;(2)对于阈值的选择影响到避障性能优劣。针对以上问题,本节针对具体场景进行建模分析,提出基于陷阱检测机制与动态阈值的VFH算法,仿真验证所提出改进策略的有效性。
3.1 基于陷阱检测机制的VFH算法
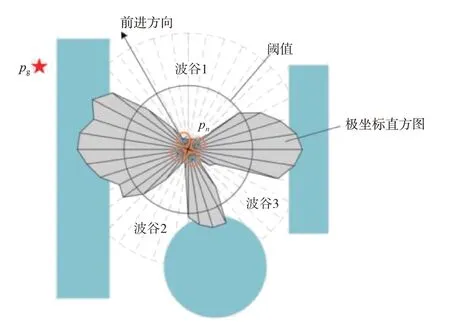
图5 VFH算法示意图Fig.5 VFH schematic diagram
本文将历史时刻栅格信息作为记忆栈,并根据无人机是否陷入陷阱来动态选取记忆栈中的信息,以扩展VFH算法的记忆性。
首先设计了一种陷阱检测机制,以实时判断是否陷入了局部陷阱,示意图如图6所示。

图6 实时陷阱检测机制示意图Fig.6 Real time trap detection mechanism
设置陷阱检测精度αtrap,将每一个全局地形栅格(i,j)划分为n个扇区,即n=,每个扇区用一个对应值trap_numi,j,k描述无人机曾经踏足栅格(i,j)且速度矢量角度φ位于扇区k的时刻信息。
(1) 初始阶段,统计值trap_numi,j,k初始化为-1。
(2)t0时刻当无人机第一次到达某个栅格点(i,j)时(发现对应trap_numi,j,k=- 1),设置此时无人机速度矢量角度φ对应扇区k的trap_numi,j,k为t0,其中。对于同一栅格点,无人机以不同角度φ′对应的扇区k′到达该栅格点,具有各自的发现时刻trap_numi,j,k和trap_numi,j,k′。
(3)设置陷阱检测时间差ttrap,当t1时刻无人机再次到达栅格点(i,j) 时对应的trap_numi,j,k> =0,当t1-trap_numi,j,k>ttrap时判断无人机已陷入陷阱,此时更新trap_numi,j,k为t1。若trap_numi,j,k>= 0 且t1-trap_numi,j,k≤ttrap,则说明有可能是由于无人机速度较慢导致在同一栅格内停留较长时间,此时不需要更新trap_numi,j,k,以避免无人机在较小范围内震荡运动时无法检测出是否陷入陷阱。
针对任意时刻获取到的障碍物信息,将其归入记忆栈中,以用于基于部分历史信息的局部避障。其示意图如图7 所示,记忆栈拥有先进后出的特性,栈中每一个元素以时间为单位,表示该时刻t新发现的障碍物栅格集合,即集合中的每一项都代表t时刻新发现的存在障碍的栅格(i,j),其对应置信度随着传感器扫描过程不断更新并用于后续VFH极坐标直方图的构建。对于图7的场景,t=1 时刻无人机第一次探测到(3, 2), (3, 3), (3, 4), (3, 5),将其作为一个集合压入记忆栈中;t= 2 时刻忽略已探测的(3, 5),将新探测到的(3, 6), (3, 7), (3, 8)压入记忆栈中。t=3 时 则 将(3, 9), (3, 10), (3, 11), (4, 11), (5, 11),(5,1 2) 压 栈。同时,对于压入栈中的集合赋予对应的下标index,该索引值从0开始依次递增,以表示障碍栅格集合压栈顺序。随着无人机运动,逐渐构建起保存所有历史障碍信息的记忆栈结构。
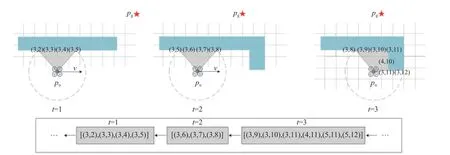
图7 记忆栈示意图Fig.7 Memory stack schematic diagram
设置索引值mt,即无人机选择从下标index为mt直到栈顶的障碍栅格集合,距离现在最近时刻发现的栅格点将会被优先取出。将集合中栅格(i,j)对应的置信度cij用于VFH算法的第二层数据缩减过程,与活动窗口中的栅格点共同构建极坐标直方图H。区别于第2节,本节在引入历史障碍信息后,定义mij即栅格的障碍物确定度为mij=(a'-b'dij),其中,b'=b,其中,dmax是无人机当前位置到活动窗口中最远栅格的距离,d′max是无人机当前位置到记忆栈选择出的最远栅格距离,通过以上方式可以避免栅格位于活动窗口之外导致的mij< 0。
历史信息的选择阈值mt并非一个定值,其随运动过程中是否陷入陷阱而动态变换,以适应不同场景中的选取策略:当未陷入陷阱时,mt增大以避免使用冗余的历史信息;当频繁陷入陷阱时,mt减小以加强VFH 的记忆性帮助脱困,动态阈值mt的更新策略为:当陷阱检测机制判断无人机陷入陷阱时,mt=mt-gt,其中gt设计为大于1 的正整数,以避免无人机脱困后mt难以追上记忆栈栈顶的情况;当无人机踏足新栅格点,即栅格点(i,j) 的n个扇区都有trap_numi,j,k=-1,其中k= 0, 1,…,n-1时,mt=mt+gt。
根据本节提出的记忆信息选取策略,无人机在正常运动或陷入陷阱时的局部规划策略是相同的,历史信息选取数量会随着无人机状态的改变而发生动态变化,以适应不同场景下的VFH记忆性需求。
3.2 基于动态阈值的VFH算法
VFH 算法中如何选择合适阈值是一个重要问题,无人机需要在避障与尽可能到达目标这两者之间均衡。在原VFH算法中,阈值T大多数时候是基于经验的,这种方式虽然较为简便,但是不利于未知复杂环境的有效避障。本文设计基于动态阈值的VFH算法,根据周围环境情况自适应更新阈值T,以帮助无人机更好地在不同场景条件下进行局部规划。
如图8所示,希望在复杂场景中提高T以获得更多可选方向,避免传统VFH算法由于固定阈值可能出现的无解情况,并在脱离复杂环境后减小T以增强避障能力。
阈值T的自适应更新可能会增加部分非安全的波谷对应的无人机备选方向,此时需要考虑无人机运动过程中的安全性问题,即无人机应该与障碍物边界保持一定的安全距离ds。因此,对传统VFH中的部分窄波谷进行修正,对第m个波谷的起始和终止角度边界值αm_begin和αm_end,定义修正量am_begin及am_end。
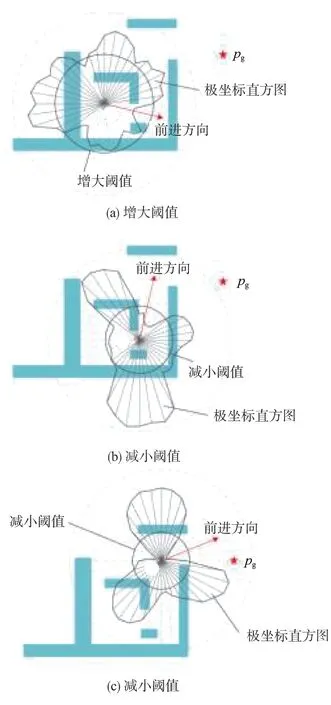
图8 动态阈值示意图Fig.8 Dynamic threshold schematic diagram
式中,dm_begin是波谷起始边界障碍物与无人机间距,dm_end是波谷终止边界障碍物与无人机间距。将起始和终止角度边界 值αm_begin和αm_end修 正 为α'm_begin=αm_begin+am_begin和α'm_end=αm_end-am_end。修正后的第m个波谷的跨越扇区角度为(α'm_begin,α'm_end)。当α'm_begin≤α'm_end时,波谷m满足无人机安全距离,可产生备选方向;否则跨越扇区范围过窄,需要忽略掉该扇区以首先保证无人机安全性。
如图9所示,设置最大阈值Tmax为极坐标直方图H中的最大值,即动态阈值T不能大于Tmax,避免对障碍地形的过度忽略。阈值T动态更新策略为首先计算各个波谷中满足安全边界距离的POD最大值h'i_max,从各个波谷的h'i_max中选择最小值h'min,根据该最小值h'min和最大阈值Tmax计算动态阈值T,具体如下:
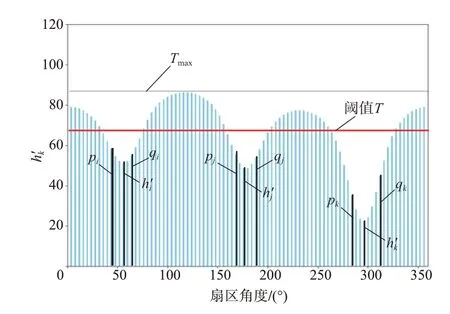
图9 阈值选择示意图Fig.9 Threshold selection schematic diagram
(1)由极坐标直方图H中n个波谷扇区的POD 极小值h′k,k= 0, 1, …,n- 1,构成集合M,其中第i个POD极小值h′i对应角度属于第i个极小值扇区,h′i∈M。
(2)针对第i个极小值扇区,其跨越角度范围为(βi_begin,βi_end)且满足βi_end-βi_begin=ar。根据无人机障碍边界安全距离ds,计算到极小值扇区中心的角度修正量,从而得到安全波谷范围为(pi,qi)
式中,βpi_begin为扇区pi的角度左边界,βqi_end为扇区qi的角度右边界;dpi为扇区pi中的障碍物与无人机最近距离,dqi为扇区qi中的障碍物与无人机最近距离。
(3)根据获得的包含扇区i的安全波谷范围(pi,qi),通过极坐标直方图H,选择该安全波谷范围中各角度对应POD值的最大值h'i_max,其中pi≤i_max ≤qi。
(4)从多个波谷得到多个h'i_max,选择其中最小值h′min=min(h'i_max),i= 0, 1, …,n-1为基准计算阈值T
式中,λt为动态阈值增益系数,是满足0 <λt< 1的常数。
针对图8 场景中固定阈值可能导致的无解问题,通过上述动态阈值策略基于Airsim仿真验证方法的有效性。设置40 × 40m的二维平面区域,无人机起始坐标为(0,0)m,目标坐标为(12,12)m,约束无人机最大速度为vmax=2m/s。设置激光雷达最大探测半径为dr= 12m、探测精度为ar=5°。对于VFH 算法中的参数,设置栅格大小为0.5m × 0.5m,活动窗口大小为25m × 25m,障碍物确定度常数a=12,b由活动窗口大小和a的值确定,实时陷阱检测精度αtrap=,记忆信息增量gt=2,安全距离ds=1.5m,动态阈值增益系数λt=0.5,无人机控制律增益系数η= 0.5。在距离无人机初始位置较近区域存在较密集障碍物,且对目标造成遮挡。仿真步长设置为0.1s,仿真结果如图10所示。

图10 无人机运动过程Fig.10 UAV motion process
由仿真结果可知,由于无人机的探测半径较大且障碍物对无人机呈包围分布,因此传统VFH算法的固定阈值策略使所有扇区均处于波峰,没有无人机的可选运动方向。根据本节提出的策略,通过极坐标直方图中具体数据信息动态更新阈值,从而扩展波谷扇区范围,增加无人机备选方向,帮助无人机脱困。改进的VFH算法流程如图11所示。
3.3 无人机整体避障策略
本文采用A*算法作为全局规划部分,且A*中的栅格与静态已知障碍物的栅格划分规则保持一致(此处用于全局规划的栅格矩阵M与局部规划部分的障碍物置信度矩阵C的栅格精度并非一致)。经过A*算法,无人机得到一条避过静态已知障碍物的具体路径,且该路径以栅格点集的形式表示。无人机跟随该路径开始运动,按照顺序设置全局规划结果点集中的栅格点为临时目标点,并通过激光雷达传感器进行实时地形探测。当感知到周边地形覆盖了临时目标点时,使用上文中基于改进VFH 算法的局部规划策略,并更新临时目标点为全局规划结果点集中的下一个栅格点,重复循环以上过程直到到达临时目标后从局部规划策略切换回全局规划策略。单无人机整体避障策略流程如图12所示。
4 仿真验证
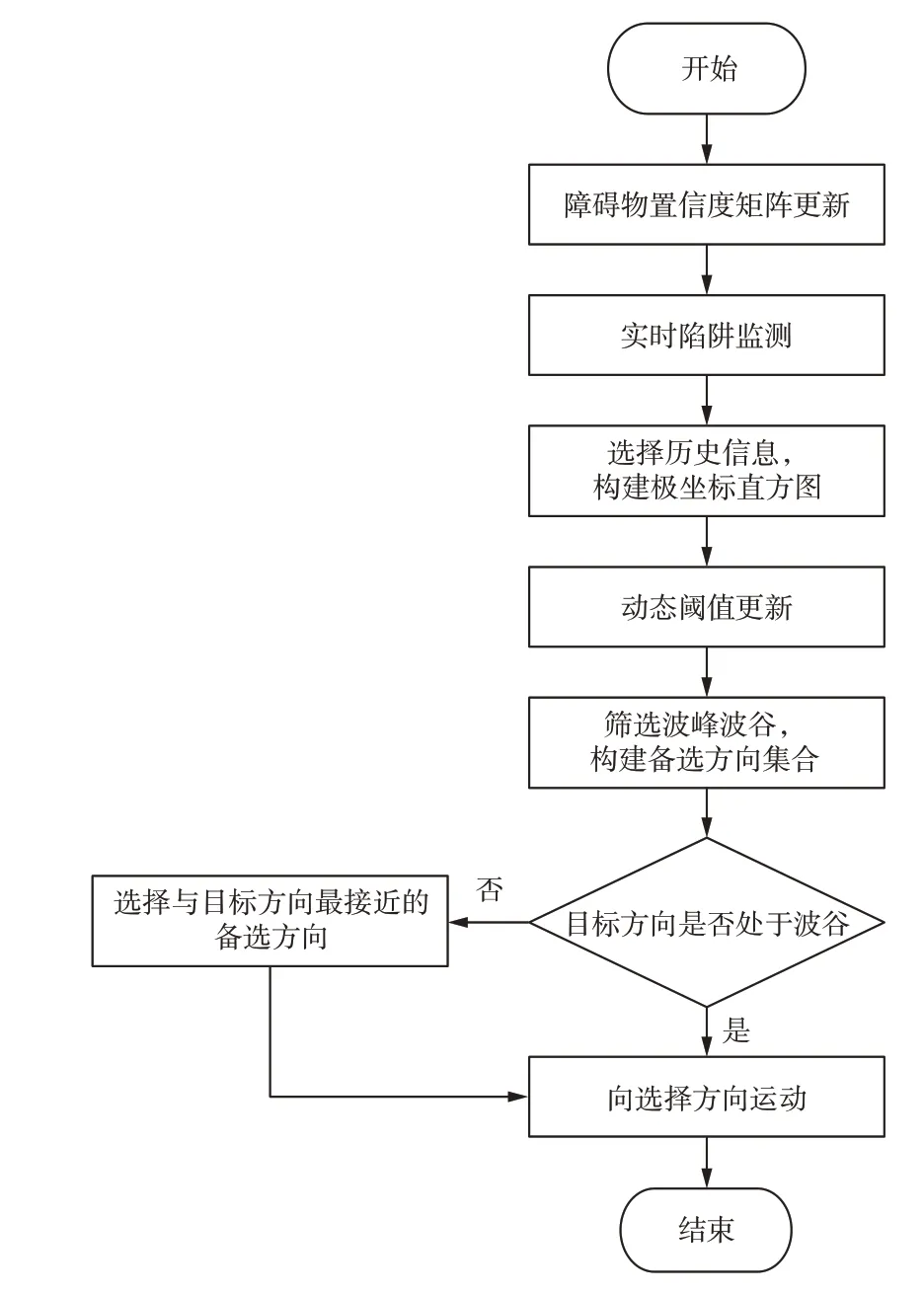
图11 改进VFH算法流程Fig.11 Improved VFH flow chart
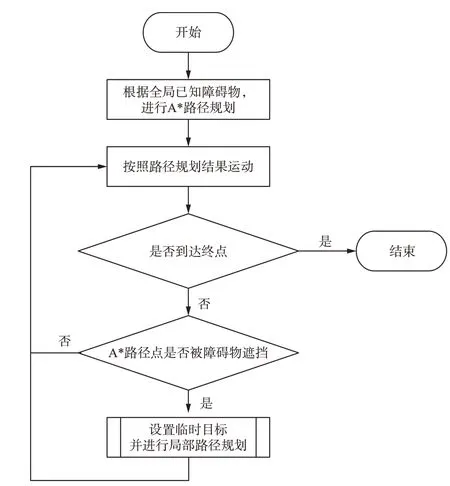
图12 无人机整体避障策略流程Fig.12 UAV overall obstacle avoidance strategy flow chart
本节对上文提出的未知复杂环境下单无人机避障策略进行仿真验证。在全局规划部分采用A*算法,在局部规划策略部分,分别采用基于传统VFH算法及本文提出的基于陷阱检测机制与动态阈值的VFH算法进行了仿真,并对比两种局部规划策略下单无人机避障效果,以验证本文提出策略的有效性。
首先基于Airsim 仿真平台进行环境搭建,如图13 所示,构建40m×40m的矩形区域,无人机起始坐标为(2,7)m,目标坐标为(38, 32)m,约束无人机最大速度为vmax=1.5m/s,地图栅格精度dg=0.5m,激光雷达最大探测范围dr= 4m、水平探测精度ar=5°。

图13 基于Airsim的仿真场景搭建Fig.13 Simulation scenes based on Airsim
以栅格点集的形式设置静态已知障碍物,图14中的黑色矩形即为无人机起飞前的已知地形。根据基于A*算法的全局规划策略进行路径规划,图14中的蓝色点集即为规划结果。无人机需要以全局规划结果作为飞行路径,并通过激光雷达传感器实时感知地形信息判断是否需要切换到局部规划策略。
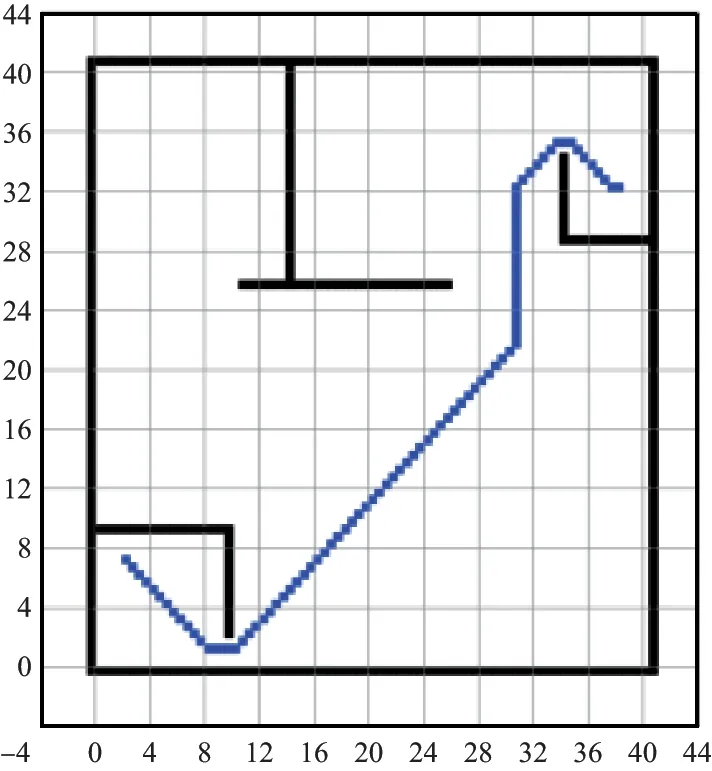
图14 全局路径规划结果Fig.14 Global path planning
(1) 基于传统VFH算法的局部规划策略
针对局部规划下传统VFH算法对无人机的运动控制,对激光雷达点云进行三层数据减缩处理,设置障碍物置信度栅格精度为0.25m × 0.25m,活动窗口大小为10m × 10m,障碍物确定度常数a= 4,b由活动窗口大小和a的值确定,无人机控制律增益系数η= 0.5。无人机运动过程如图15所示。
无人机在t= 15s 左右处于局部路径规划策略,无人机与目标间有连续密集障碍物,由于传统VFH算法的无记忆性与贪心的规划策略导致无人机会在一定空间区域内来回震荡运动,即陷入了陷阱。这也是许多局部路径规划算法存在的问题,即短视的规划策略导致仅仅能够避过附近障碍,在复杂场景下不具有有效性。
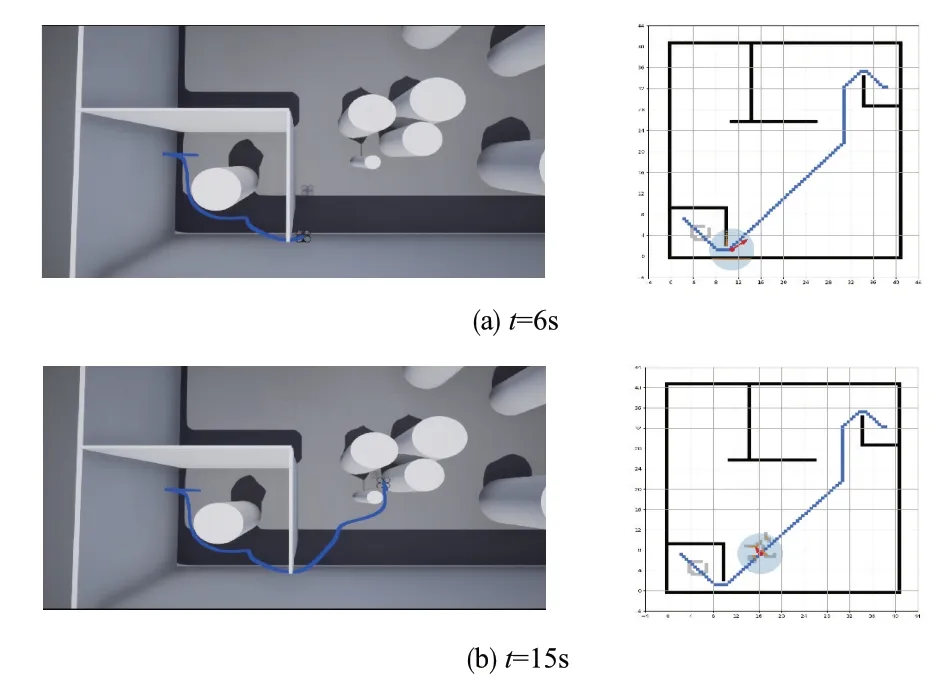
图15 基于传统VFH算法的无人机运动过程Fig.15 UAV motion process based on traditional VFH
(2) 基于改进VFH算法的局部规划策略
针对局部规划下改进的VFH 算法对无人机的运动控制,在传统VFH 的基础上引入陷阱检测与动态阈值机制,对其中涉及参数设置实时陷阱检测精度αtrap=,记忆信息增量gt= 3,安全距离ds= 1.5m,动态阈值增益系数λt= 0.7,其他传统VFH 算法中涉及参数与改进前VFH 算法仿真参数保持一致。无人机运动过程如图16 所示。无人机运动状态、t= 15s 时,无人机同样处于局部规划策略,但是实时陷阱监测机制根据无人机的重复震荡运动判断出无人机已陷入陷阱,动态调整VFH 算法的记忆性,通过记忆栈扩展极坐标直方图中的扇区障碍物信息以帮助无人机脱困。与此同时,动态阈值策略保证在复杂或稀疏的不同场景中都能有合理的波谷筛选阈值,让无人机有更多的备选方向。
对比改进前后VFH算法的仿真结果,本文提出的基于陷阱检测机制与动态阈值的VFH 算法能够解决传统局部规划算法中的易陷入局部陷阱的问题,更加符合未知环境下无人机路径规划的要求。
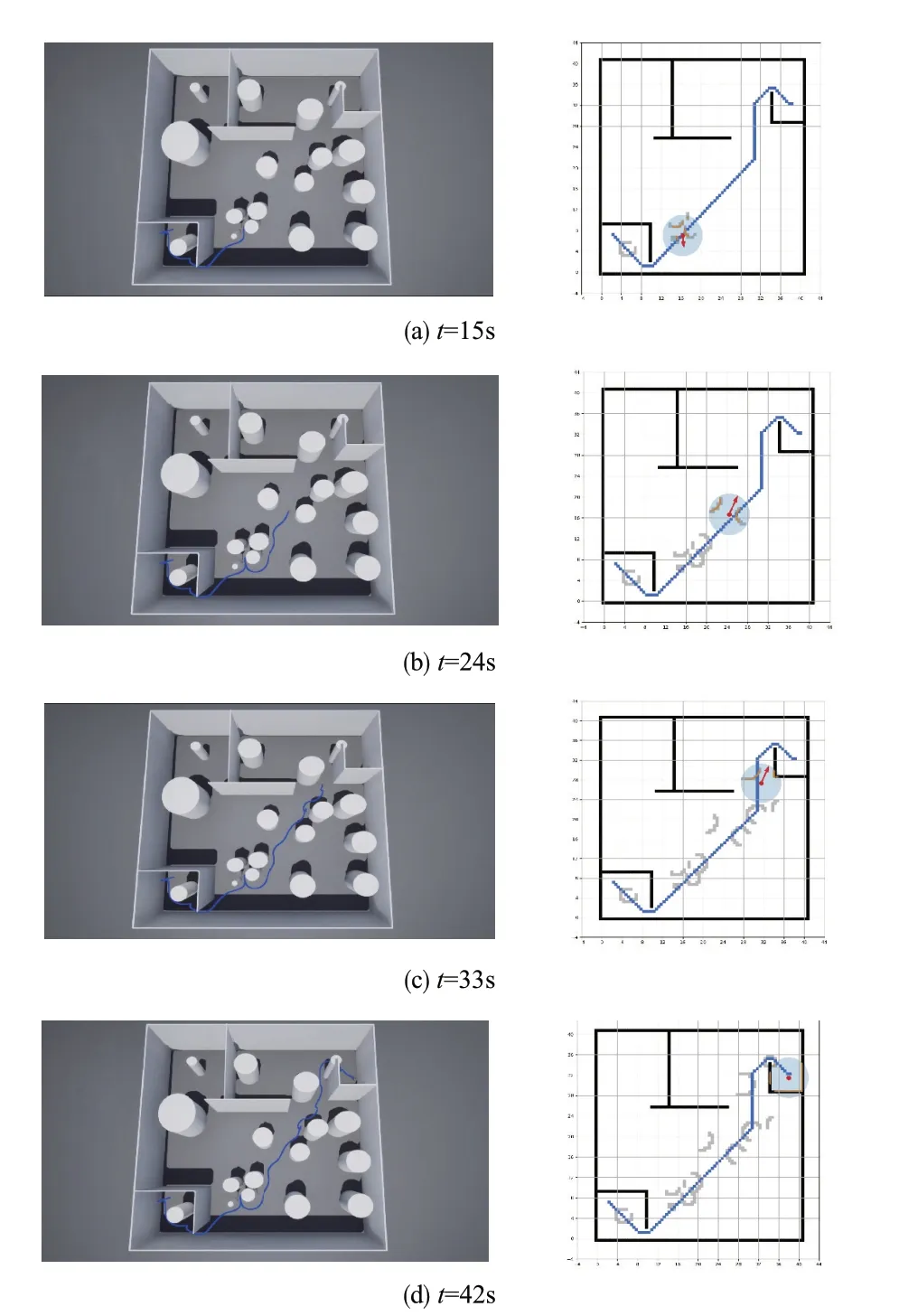
图16 基于改进VFH算法的无人机运动过程Fig.16 UAV motion process based on improved VFH
5 结论
本文针对未知复杂环境下的无人机路径规划问题,提出了一种全局规划基于A*算法与局部规划基于改进VFH算法的避障策略。首先进行无人机避障环境建模,并对传统VFH 算法进行详细介绍并阐述其局限性。针对VFH 算法的无记忆性问题,设计了一种实时陷阱检测机制,根据无人机运动状态动态选择历史栅格信息以避免陷入局部陷阱;针对VFH 算法的阈值敏感性问题,设计了一种动态阈值更新策略,增强算法在不同场景中的有效性。最后通过Airsim对比仿真验证了本文提出算法的有效性。

