一种基于直升机毫米波雷达的高压线RCS快速计算方法
陈春风,李聃,陈昌年
1.航空工业雷华电子技术研究所,江苏 无锡 214063
2.南京航空航天大学 教育部雷达成像与微波光子学重点实验室,江苏 南京 210016
直升机的应用十分广泛,其从诞生以来,就一直受到世界各国的高度重视[1-2]。电力线对直升机的安全构成最严重的威胁[3-4],因此电力线的检测一直是直升机防撞研究的重点。高压线探测早期应用激光或红外设备,由于不能实现全天候检测,毫米波雷达成为最主要的传感器,是全天候电力线探测的有效手段[5]。绞股高压线的特性是会在毫米波段产生布拉格(Bragg)散射[6]。随着机器学习和深度学习算法的兴起,学习算法得到了发展,开发的算法(包括SVM[7]和CNN[8])具有较好的性能。然而,高压线的种类不是一成不变的,少量的有限种类的高压线训练出来的算法虽然对训练过的高压线检测能力强,但若遇到新的与训练用的高压线回波的Bragg强度等特征差异大的回波,反而会影响检测性能,即泛化能力不好。因此,在复杂地形情况下,需要大量高压线的Bragg散射样本来提高基于布拉格散射的最大似然法(ML)检测方法的泛化性。由于试验录取数据的成本昂贵,通过试验获取大量样本是不现实的。因此,有必要探索快速且有效的仿真算法来获得不同类型和规格的高压线雷达截面积(RCS)样本用于训练,进而满足学习算法的需求。
电磁计算领域有很多RCS 仿真方法,如高频近似方法[9-10],包括几何光学(GO)和物理光学(PO),已用于有效计算高压线的RCS。然而,GO 和PO 的计算精度并不令人满意。虽然上述两种方法可以获得布拉格散射的角度位置,但它们不能准确地反映高压线布拉格散射的振幅信息。与高频(GO、PO 等)近似方法相比,基于积分方程的MoM[11]通过将积分方程转换为矩阵方程,可以提供更准确的RCS 结果。另外,特征模(CM)方法[12]是一种有效的直接求解算法,通过构造特征模宏基函数显著减少了基函数的数量,从而阻抗矩阵的维数显著变小。因此,矩阵求逆时间和存储量相应地也显著减少。然而,随着目标电尺寸的增加,CM方法所需的缩减矩阵方法会变得越来越大,这使得在求解电气大型高压线时非常耗时并占用大量内存。
为了快速计算高压线RCS,本文提出了一种结合CM和谢尔曼-莫里森-渥德雷公式算法(SMWA)直接求解算法的高效直接求解法。通过CM 方法显著降低矩阵的维数,再采用SMWA 高效地求解通过CM 方法缩减的矩阵方程。数值结果表明,该方法可以以较少的内存和计算时间获得精确的高压线的RCS。同时发现了Bragg点随频率走动的特性,这为高压线检测提供了一个新的思路。
1 高压线Bragg特征
高压线的物理结构一般是铝绞股或钢芯铝绞股线,直径在10mm以上的长距离传输的高压线为了防止被应力或重力拉断,大都采用钢芯铝绞股。图1 给出了型号为LGJ50-8的典型高压线仿真模型,该高压线由1根钢芯和6根外围铝绞股线缠绕而成。

图1 高压线形状Fig.1 Geometry of power lines
图1中,两根绞股之间的距离为ρ,P表示单根绞股线的绕线周期,D代表绞股线的直径,d代表最外层单根铝绞股线的直径。该高压线具体参数见表1。

表1 LGJ50-8高压线参数Table1 Parameters of the power line LGJ50-8
低空架设的高压线根据传输要求,所使用的线型很多,参数D、P、ρ会有所变化,单根铝线d一般为1~5mm,是毫米波长尺寸,这使得高压线在毫米波频率产生Bragg 回波(见图2),有利于毫米波雷达进行高压线检测。在毫米波段,频率为35GHz、76GHz 和94GHz 的电磁波传播损耗最小。
高压线Bragg的特征原理如图2所示,由于电磁波带有相位信息,当接收到的电磁波相位相同时,波峰叠加使得反射最强,考虑高压线绞股周期结构,当入射波到达相邻绞股线表面的波程差为1/2波长的整数倍时,其后向散射回波将同相叠加,即入射角满足Bragg 反射的特征。则可以得到Bragg反射信号的回波强点公式
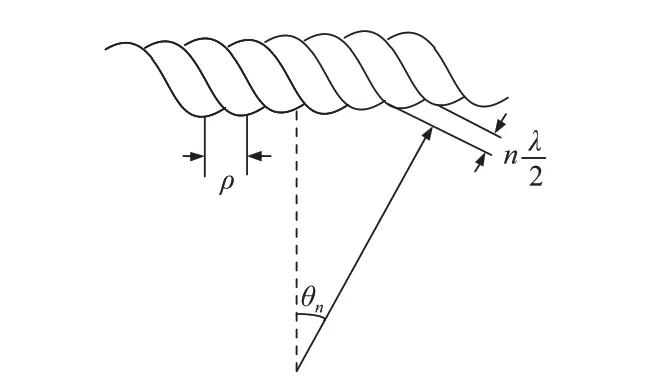
图2 高压线Bragg散射原理图Fig.2 Bragg scattering principle of power lines
式中,θn为第n个散射峰值角度;λ为波长。在特定的入射角θn出现散射峰值的现象叫作Bragg散射,θn=0° 表示垂直于高压线的主瓣,其他峰值角度称为副瓣。
2 CM-SMWA算法计算高压线
由于高压线在毫米波段的仿真需要大量的RWG 基函数,MoM 方法计算RCS 虽然能获得精确解,但基函数的数量庞大,需要高的计算量和大的存储空间,计算受到限制。而传统的CM 方法虽然减小了矩阵维数,但是计算效率仍然有待提高。本文为了实现更快速计算、占用存储资源更少,提出了一种基于CM-SMWA 的RCS 计算方法,该方法将CM 与SMWA 相结合[13],以减少传统CM 方法的内存和计算时间。
2.1 简单分组的CM-SMWA方法
单层二叉树划分的CM-SMWA将RWG基函数分为两组,对应矩阵为
式中,Z11和Z22分别为组1 和组2 中的RWG 基函数的自阻抗矩阵。Z12和Z21是RWG基函数组1和组2之间的互阻抗矩阵,它们可以通过自适应交叉近似(ACA)算法进行低秩压缩分解[14]。V1和V2是对应于组1 和组2 的电压矢量。I1和I2是对应于两组的电流系数。
SMWA被引入CM[12],并被分成两个小矩阵
式中,Ji表示保留的CM;Z12和Z21可以通过ACA算法[14]压缩为
Z12和Z21的有效秩比N/2 的小得多。将式(4)代入式(3),可以得到式(5)
经过计算,得到式(8)
在等式(8)中,I表示单位矩阵。使用SMW 公式[15],最终可获得式(11)
I1≈J1α1和I2≈J2α2是RWG基函数的近似电流系数。
2.2 更多分组的CM-SMWA方法
虽然单层二叉树可以在一定程度上减少计算机存储空间,但矩阵仍然很大,减少计算量的效果有限。为了尽可能减少计算量,有必要对二叉树进行进一步分组。对于多层算法(假设为L级),CM-SMWA算法的步骤如下。
(1) 生成最底部的块对角矩阵并找到CM
(2) 使用CM压缩最底部的对角矩阵
3 算力分析
3.1 仿真评估方法
本文中,使用计算时间、内存消耗和仿真精度来衡量所提出的RCS计算方法的性能。特别是采用MoM的结果作为参考结果,并使用均方根误差(RMSE)作为目标函数来计算本文提出的方法的仿真精度
3.2 数值仿真
由于76GHz可以用作低成本或片上雷达[16],本文主要基于76GHz 的频点进行仿真研究。高压线的长度选择为P=0.138m,目标由平均边长为0.1λ的RWG基函数离散,由于该波段的波长较短,需要为仿真建立更多的基函数。总共使用81822 个基函数。二叉树的级数为L=7,这意味着高压线被分成128段。每个段的CM数量固定为300,用于生成CM的每个段的扩展设置为0.1λ。
H-H 极化的仿真结果如图3 所示,V-V 极化的结果如图4 所示。可以看出,具有较大误差的角度主要集中在最小值,并且由于在实际雷达检测中,高压线的回波受到地面杂波的影响,该“最小点”误差比地面杂波弱,因此这些误差对于高压线仿真而言是可以接受的。
表2显示了在76GHz仿真下通过不同算法计算的高压线结果的比较。本文方法在CPU 时间和存储方面具有明显的优势。
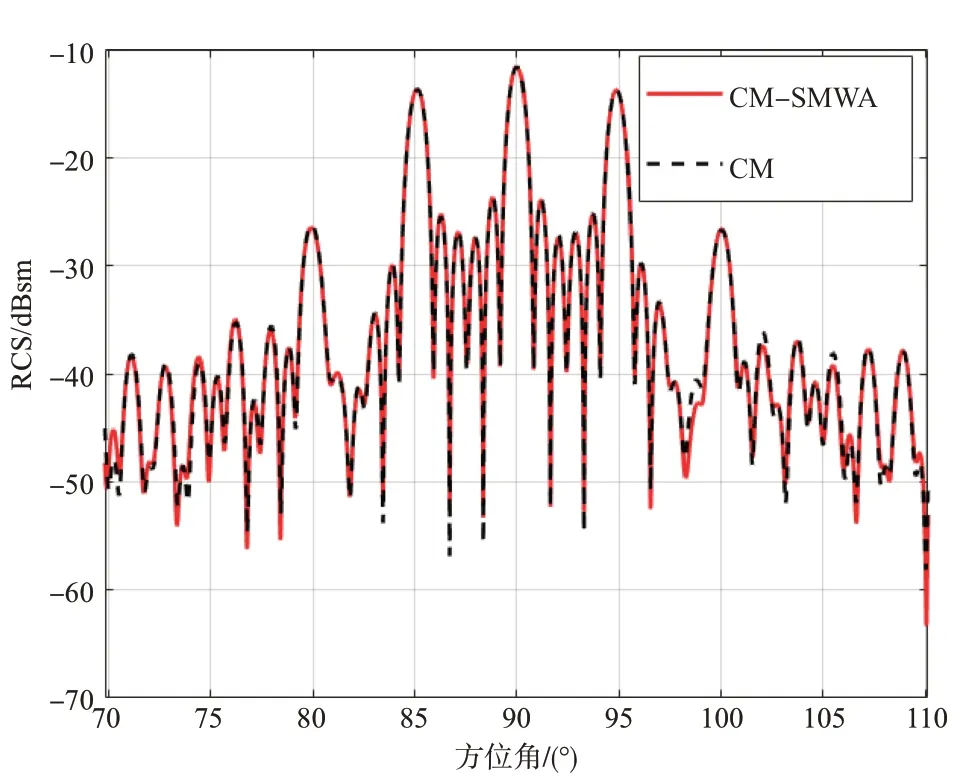
图3 76GHz(H-H)下高压线RCS仿真结果Fig.3 Simulation results of the power line RCS at 76GHz(H-H)
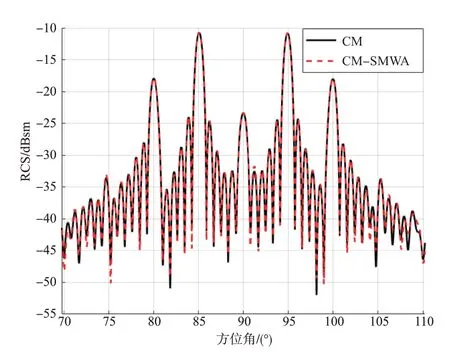
图4 76GHz(V-V)下的高压线RCS仿真结果Fig.4 Simulation results of the power line RCS at 76GHz(V-V)
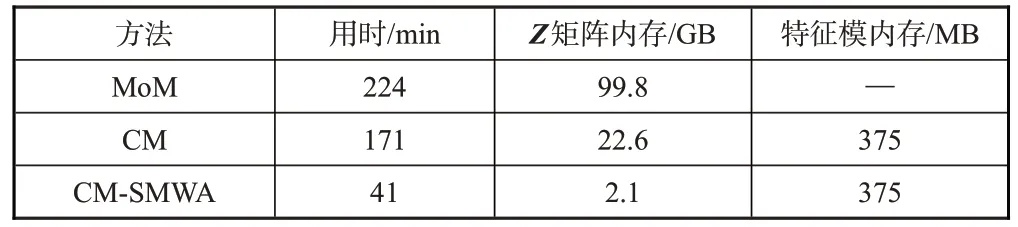
表2 三种不同方法的高压线仿真性能对比Table 2 Comparison of the CPU time and memory requirement between the different algorithms at 76GHz
图5 比较了更多基函数条件下的76GHz 仿真,仿真长度为73.6cm,仿真高压线基函数为440000个,这是MoM方法难以仿真的。用于查看不同频率差异的Bragg回波点的位置差异。
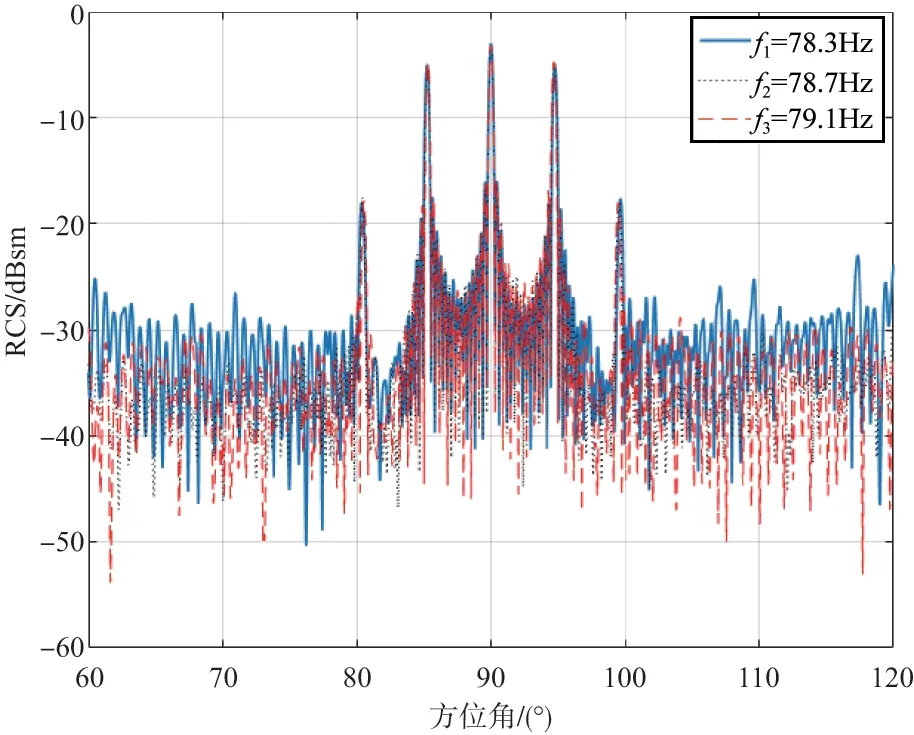
图5 长度为73.6cm高压线的RCS结果Fig.5 RCS results for power lines with a length of 73.6cm
如图5 所示,仿真长度为73.6cm,高压线的Bragg 点的宽度更窄,仿真频率由低到高渐变,根据式(1),频率变高后Bragg角度会变化,且n=2的Bragg点比n=1的Bragg点变化大。本文进行了不同频率条件下的Bragg 位置变化分析,如图6和图7所示。
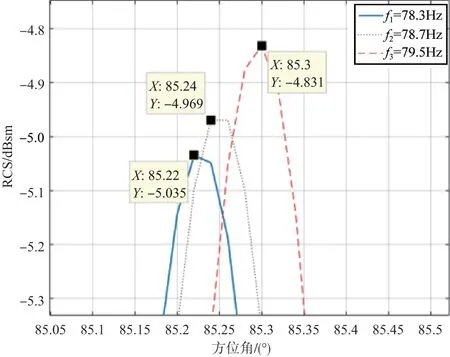
图6 随着频率增加Bragg点位置变动(n=1)Fig.6 Changes in Bragg point position with increasing frequency (n=1)
从图6和图7可以看出,随着频率的增加,Bragg点会向着垂直点(90°)移动,f2和f3频率差异相比于f1和f2更大,则相对于f1和f2角度移动得更剧烈。图7中n=2的Bragg点的位置相对于n=1 的Bragg 点位置离垂直点更远,由式(1)可以看出,f1和f2之间n=1位置的Bragg点移动0.02°,则n=2位置的Bragg 点移动了0.04°。仿真结果满足理论,说明仿真的Bragg点位置同样准确。
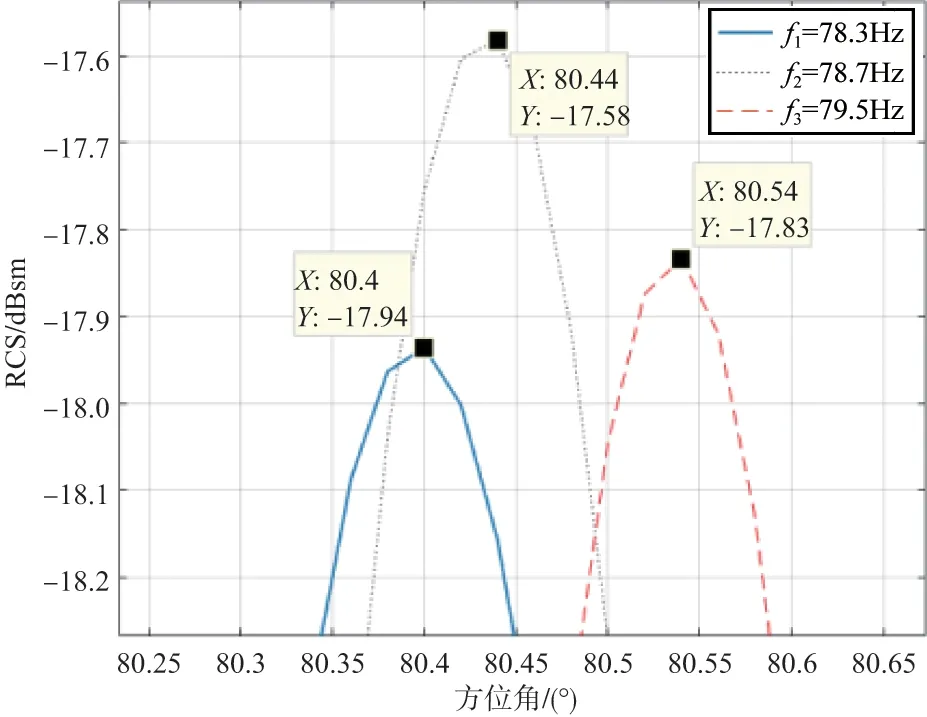
图7 随着频率增加Bragg点位置变动(n=2)Fig.7 Changes in Bragg point position with increasing frequency (n=2)
4 结论
本文提出了一种将CM与SMWA相结合的高压线RCS仿真方法,并采用此方法进行多频点的Bragg 走动验证。仿真结果表明,该方法在RCS计算的内存需求和计算时间方面都优于传统的MoM和CM方法。76GHz试验表明,与传统MoM 相比,对于长度为0.138m 的典型LGJ50-8 高压线,计算时间减少了81.6%,内存占用减少了97.5%。高压线RCS 仿真表明,随着频率变化,Bragg 走动特征比较明显,该特征可以用复杂地物环境下高压线来识别。Bragg频率走动特征与地面的其他目标差异较大,如果设计宽带毫米波雷达,通过频率来提取该特征,将使毫米波雷达极大提升直升机在复杂环境下高压线检测的性能,高压线检测性能提升后,直升机更容易发现预警高压线,在低空高速复杂环境下飞行将更加安全。

