基于加速度多重基线校正的移动车辆下桥梁动位移间接测量方法

林国伟, 王铭巍, 李岩*, 马俊

(1.济南城建集团有限公司, 济南 250000; 2.哈尔滨工业大学交通科学与工程学院, 哈尔滨 150090)

桥梁结构位移测量在桥梁荷载试验检测与健康诊断中占有重要地位,通过位移可以对桥梁的实际刚度和服役状态进行判断。常用的接触式位移测量传感器精度较高,但在实际测试过程中容易受环境条件和结构形式限制而难以找到相对静止参考点,或测试需要支架等固定参考点导致测试实验准备工作耗时费力[1-3]。典型的非接触式方法如全球定位系统(global positioning system,GPS)测试精度仅适用于变形较大的大跨度柔性体系桥梁,无法用于中小跨度桥梁;近年基于机器视觉的位移测量方法成为研究热点,但距离实用尚存在一定距离;同时,对光线和天气的敏感程度也限制了其在交通基础设施维护的广泛应用[4-7]。与之相比,加速度计无需固定参考点,且成本较低、易于布置,而桥梁位移响应理论上可以通过加速度信号积分的方式得到,因此基于测量的加速度进行位移间接估计已经被提议作为桥梁位移测量的有效方法[8-10]。

通过加速度信号积分得到位移主要有时域积分和频域积分两种方法。频域积分的运算中低频噪声会对积分结果起到支配作用,而加速度频谱信号的低频部分又包含着结构的准静态响应[11],因此采用截止频率进行高通滤波减小误差的方法并不可靠,导致频域积分对于传感器的低频精度要求较高。时域积分中振动信号的微小误差会累积放大使最终结果偏离实际值,产生基线漂移。陈为真等[12]提出了利用拟合多项式极值消除时域积分产生的误差趋势项的方法,得到了具有较好精度的位移时程曲线,但该方法仅对线性趋势项和常数误差项起作用,无法消除随机噪声产生的误差。Sekiya等[13]采用分离自由振动的方法,对强迫振动和自由振动分别进行积分并进行简单基线校正。经过尝试发现只有在采用高分辨率和低噪声的加速度传感器的情况下才能积分得到与实测位移相近的结果,说明该方法并不能完全消除传感器噪声产生的误差。Umekawa等[14]将加速度直接二次积分后以样条曲线拟合误差趋势项进行基线校正,但这种方法只适用于基线漂移不严重的情况,因此对于精度较差的传感器信号积分,有效地误差消除方法有待研究。Zheng等[15]联合基于递归最小二乘法、递归高通滤波器和递归积分器,通过多轮基线校正、滤波和积分,提出了一种在线实时加速度积分方案,结果表明利用最小二乘法进行基线校正可以有效减小加速度积分误差。但由于将速度和位移基线校正的目标基线设置为零水平线,导致该方法不能直接应用于桥梁不围绕零水平线振动的情况如车致振动等场景。

为此,现针对移动车辆过桥这一桥梁运营和动载试验中典型场景,提出一种基于动静分离和最小二乘法加速度时域积分的桥梁位移响应测试方法,并构建一种更加有效的基线校正策略。通过一座实桥现场试验对所提出方法的精度和适用性进行试验验证及相关参数分析。

1 基于实测加速度的移动车载下桥梁动位移估算方法

1.1 方法的框架和实现流程

由于加速度传感器测试得到的加速度信号与实际值会有一定偏差,该偏差在数值二重积分过程中会累积导致结果产生基线漂移。这种偏差存在于整个频段中,其带来的误差无法通过滤波完全分离[14],而需要参考数据整体的偏离情况进行校正。移动车辆作用下桥梁动力响应可视作自由振动响应和准静态响应的叠加,二者的基线并不相同,需分别考虑其各自基线校正方法。考虑移动车辆作用下桥梁动力响应及加速度测试信号特点,联合应用低通和带通滤波及多轮基线校正等误差处理方法,提出了一种新的基于加速度时域积分的位移响应估计算法,具体实现流程如图1所示。

fb为动静响应界定频率;fu为上限截止频率图1 基于动静分离和最小二乘法的加速度积分方法流程Fig.1 Flow diagram of the displacement estimation method based on dynamic-static separation and least squares method

现对所提出方法的具体实现流程总结如下。

步骤1从实测加速度数据中,截取汽车前轴上桥至后轴下桥的时间段。

步骤2采用最小二乘法对原始加速度数据进行第一次校正处理。

步骤3利用快速傅里叶变换(fast Fourier transformation,FFT)通过滤波得到准静态加速度和自由振动加速度。

步骤4将动静加速度分别积分得到速度。

步骤5对于自由振动速度,通过最小二乘法进行基线校正;对于准静态速度,采用减去均值的方法进行基线校正。

步骤6将动静速度分别积分得到位移。

步骤7对于自由振动位移,通过最小二乘法进行基线校正,对于准静态位移,不再进行校正。

步骤8将二者叠加得到估计位移。

1.2 基于动静分离的加速度积分原理

所提出方法在对桥梁加速度信号进行积分之前,首先采用低通和带通滤波方式对加速度信号进行处理,低通滤波得到结构准静态响应,带通滤波得到结构自由振动响应并滤掉其中的高频成分,减少估算误差。

其中滤波表达式为

(1)

式(1)中:N为加速度信号实测采样点数;X(k)为傅里叶变换后的加速度信号;H(k)为滤波器的频响函数,当选用低通滤波时,频响函数表达式为

(2)

当选用带通滤波时频响函数表达式为

(3)

式中:fb为动静响应界定频率;fu为上限截止频率;Δf=f/N为频率分辨率;f为采样频率。

如将车辆通过桥梁全过程引起的桥梁位移响应视作一个振动周期,则其中动静响应界定频率fb可通过车辆过桥时间确定。滤波上限截止频率fu可通过数值仿真或动力试验测试估算对结构车激动力响应起主导作用的自振频率范围来予以确定。

在时域上,桥梁动位移可以通过加速度的二次积分得到,公式为

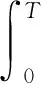
(4)

式(4)中:u(T)为T时刻位移;v(t)为t时刻速度;a(t)为t时刻加速度;v0为初始速度;d0为初始位移。

假设初始速度和位移等于0,采用梯形公式进行数值积分,位移计算表达式为

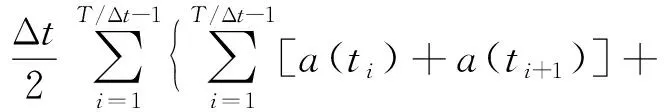
(5)

式(5)中:Δt为采样时间间隔;ti为数据采样时间点。

1.3 多轮基线校正的计算原理

为解决加速度积分得到的位移时程曲线基线漂移问题和提高积分估算位移精度,提出基于最小二乘法的多轮基线校正策略,分别对实测加速度信号及积分后速度和位移数据进行基线校正。同时,针对准静态响应基线的不可确定性,针对积分得到的准静态速度响应提出了消除均值的误差修正方法。

现对以上基线校正的原理和方法阐述如下。

1.3.1 基于最小二乘法的基线校正

采用最小二乘法拟合未处理数据的基线称为拟合基线。该方法的实质是构建一个函数,可得

(6)

寻求一个φ(t)逼近xu(ti),使其满足条件为

(7)

式中:φk(t)=tk(k=0, 1, …,m)为最佳平方逼近函数,其系数为ck,最高阶次为m;xu(ti)为未校正的数据值。

求解拟合基线目的是确定上述未校正加速度信号基线的偏移情况,从而进行校正。研究表明,以线形多项式未校正数据可以得到较好的结果[9],具体可根据桥梁实测数据进行拟合及试算确定多项式次数及系数。

将未校正数据减去拟合基线与目标基线的差值,得到校正后的曲线,即

x(t)=xu(t)-[φ(t)-f(t)]

(8)

式(8)中:x(t)为基线校正后的加速度或位移;f(t)为目标基线,对于自由振动信号,f(t)为零水平线。

1.3.2 基于消除均值的基线校正

由于汽车下桥后桥梁响应只剩下自由振动项,桥梁的静态位移恢复为0。汽车下桥时刻的准静态位移可由准静态速度根据式(5)表示为

(9)

将等式两边同时除以Δt/2可得

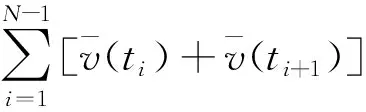
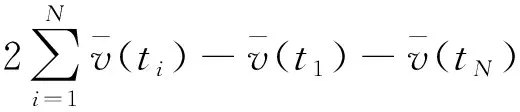
=0

(10)

(11)

基于此,提出对一次积分所得的准静态速度响应曲线校正公式为

(12)

2 工程实例应用与试验验证

2.1 工程概况与汽车动力荷载试验方案

选用黑龙江省双鸭山市西福桥作为工程实例验证所提出的位移间接估计方法。该桥例为一座预应力混凝土简支空心板桥,全长147 m,桥跨布置2×13 m+5×20 m。选取其中20 m桥跨开展汽车动载试验测试,为所提出位移估算方法应用及验证提供实测数据支持。该桥外观如图2(a)所示,半幅横断面、车辆加载位置以及传感器布设情况如图3所示。

图2 现场试验Fig.2 Field test

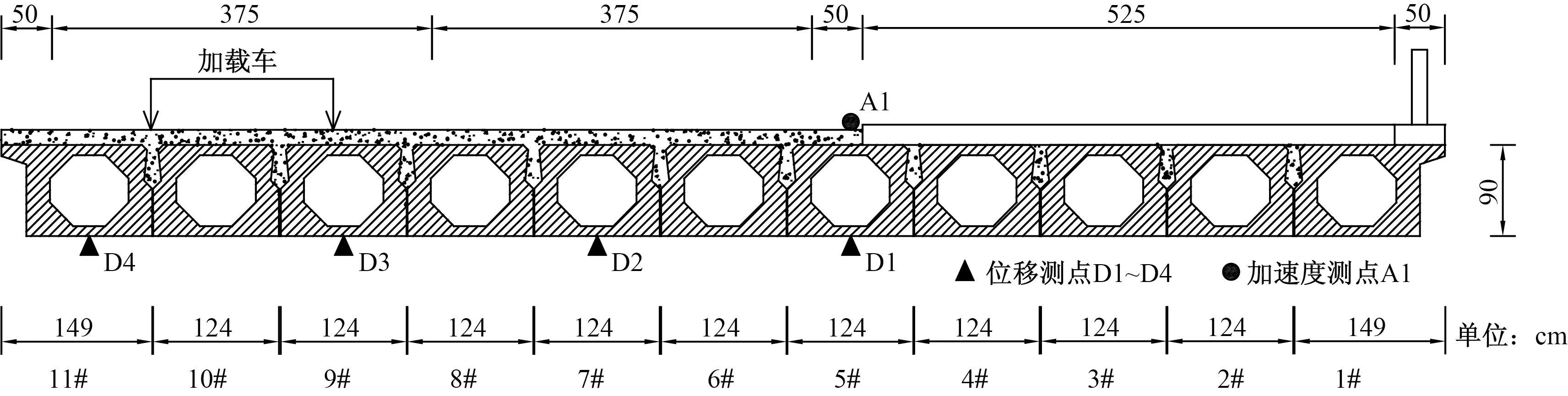
图3 半幅横断面、车辆加载位置以及传感器布设Fig.3 Half cross section, vehicle loading position and sensors layout

动载试验选用中国公路桥梁试验常用的3轴卡车,如图4所示,其参数:前轮轴重P1=6.88 t,后轮轴重P2=P3=19.61 t,前后轮轴距D1=3.85 m,前后轮距D2=1.35 m,中后轮轴距D3=1.35 m。桥梁横断面及车辆实际加载位置如图3所示。受现场试验条件限制,设置汽车以20～40 km/h不同车速匀速过桥工况。

图4 试验用加载车Fig.4 The truck used in field test

为采集移动车辆下该桥动力响应,分别于5#梁跨中布置加速度测点,5#、7#、9#、11#梁跨中布置位移测点。采用东华公司DH5922动态信号测试系统记录各测点处动力响应,采样频率为200 Hz。测试现场过程及位移传感器、加速度布置如图2(b)、图2(c)所示。现以车速30.4 km/h为例,给出实测得到的5#梁跨中加速度和位移响应如图5所示。

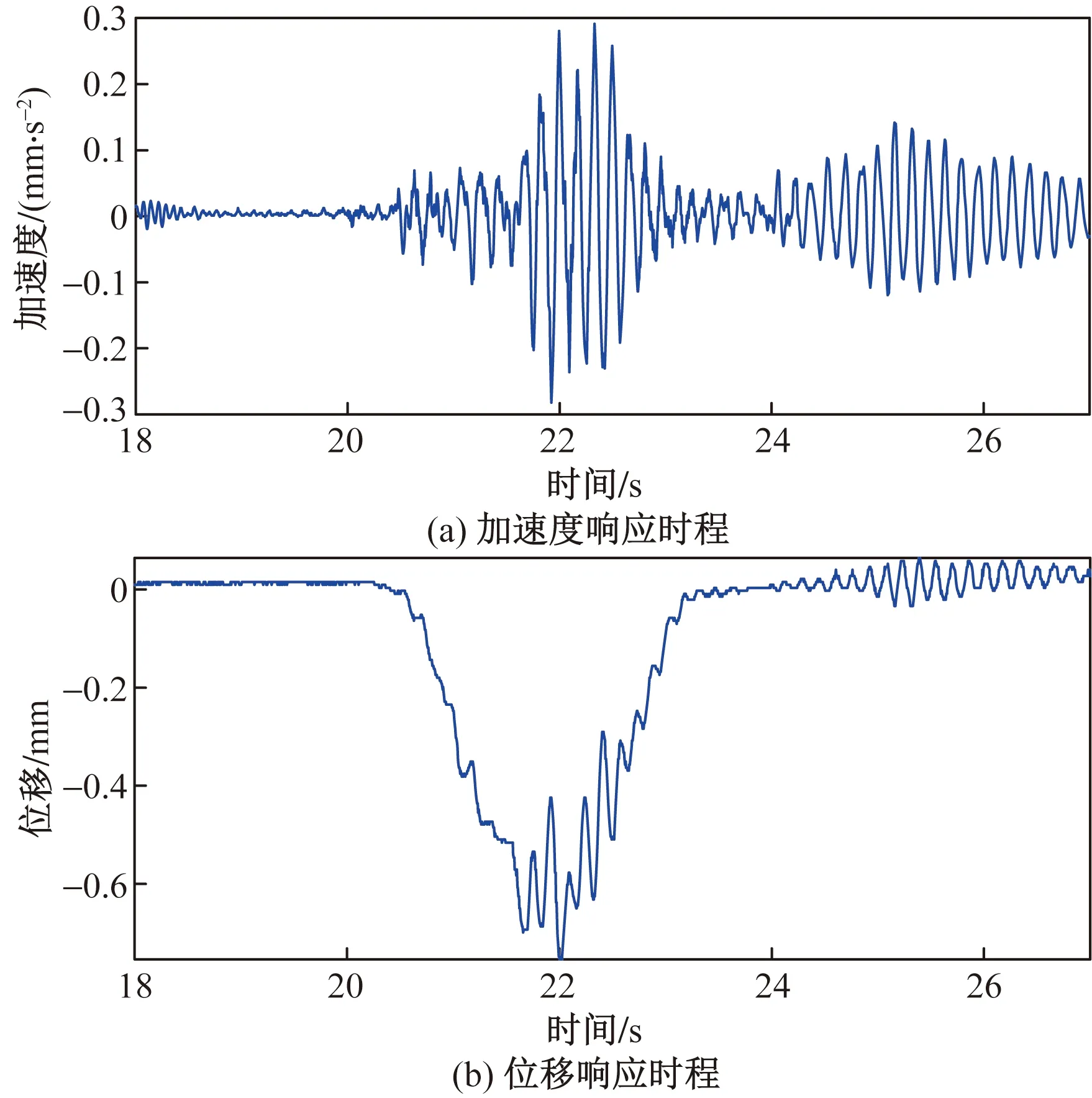
图5 汽车以30.4 km/h过桥时5#主梁跨中动力响应实测结果Fig.5 Measured dynamic response of 5# beam in mid span under moving truck at speed of 30.4 km/h

2.2 基于加速度的位移响应获取实现

选取车速30.4 km/h匀速过桥时20 m梁段5#梁跨中加速度时程信号为例,应用所提出方法进行动位移估计。首先,根据现场车辆过桥位置观测记录,准确截取汽车前轴上桥至后轴下桥的时间段。通过最小二乘法以一次函数拟合数据基线,对该加速度数据进行第一次基线校正,过程如图6所示。由数据处理前后的对比可知,加速度原始数据存在基线偏移的现象通过最小二乘法得以校正。

图6 第一次基线校正Fig.6 First baseline correction

现有研究表明,对桥梁车激动力响应起主导作用的自振频率范围包含在前几阶以内[16]。通过快速傅里叶变换对该实测信号进行频域分析,如图7所示。噪声干扰可能使高频成分中部分信号的幅值有一定的上升,因此仅考虑低频集中部分,选定滤波截止频率为20 Hz。

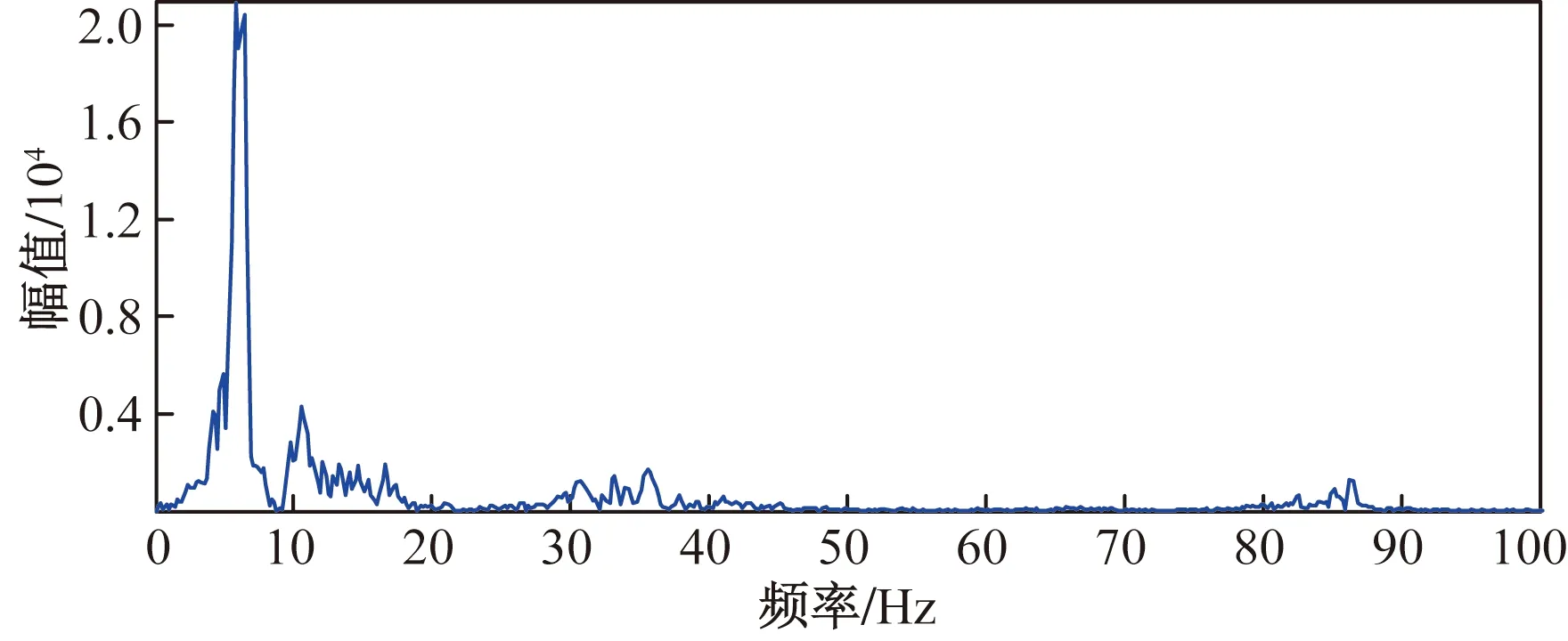
图7 加速度频谱分析Fig.7 Acceleration spectrum analysis

汽车通过桥梁时间为2.985 s,将该时间段中桥梁的准静态响应过程视作一个振动周期,则响应的频率约为0.35 Hz,由此将动静分离频率取为0.4 Hz。通过快速傅里叶变换将加速度信号分离得到准静态加速度和自由振动加速度,如图8所示。可以看出,滤波后的自由振动加速度曲线更为连续光滑,可知带通滤波可以有效地去除高频噪声干扰,后续的积分误差趋势项得以减小。

图8 加速度动静分离Fig.8 Dynamic-static separation

将上述步骤得到的准静态加速度信号进行积分,一次积分得到速度后,计算整体数据的平均值,按照所提方法进行基线校正。图9给出了积分和校正过程,可以看出,速度响应直接积分得到的准静态位移存在误差趋势项,导致产生基线漂移,而通过消除均值的基线校正能够较好地解决漂移的情况。

图9 准静态加速度积分及校正Fig.9 Quasi-static acceleration integration and correction

将自由振动加速度响应进行积分,采用所提方法,通过最小二乘法以一次函数分别拟合积分得到的速度和位移响应曲线,得到其基线并进行校正。图10给出了积分和校正过程。从积分位移基线校正前后的对比可以看出:未校正的自由振动时程曲线包含积分误差趋势项,导致基线产生漂移,而校正后的位移时程曲线更符合实际位移趋势。

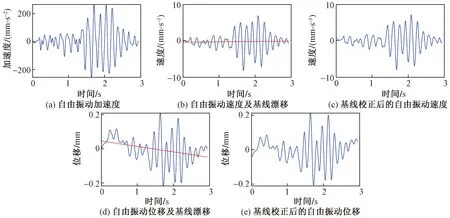
图10 自由振动加速度积分及校正Fig.10 Free vibration acceleration integration and correction

将积分得到的准静态位移与自由振动位移叠加得到最终估计位移,并与实测位移进行对比,如图11所示。可以看出估计与实测曲线形状基本吻合,说明了所提方法的有效性。

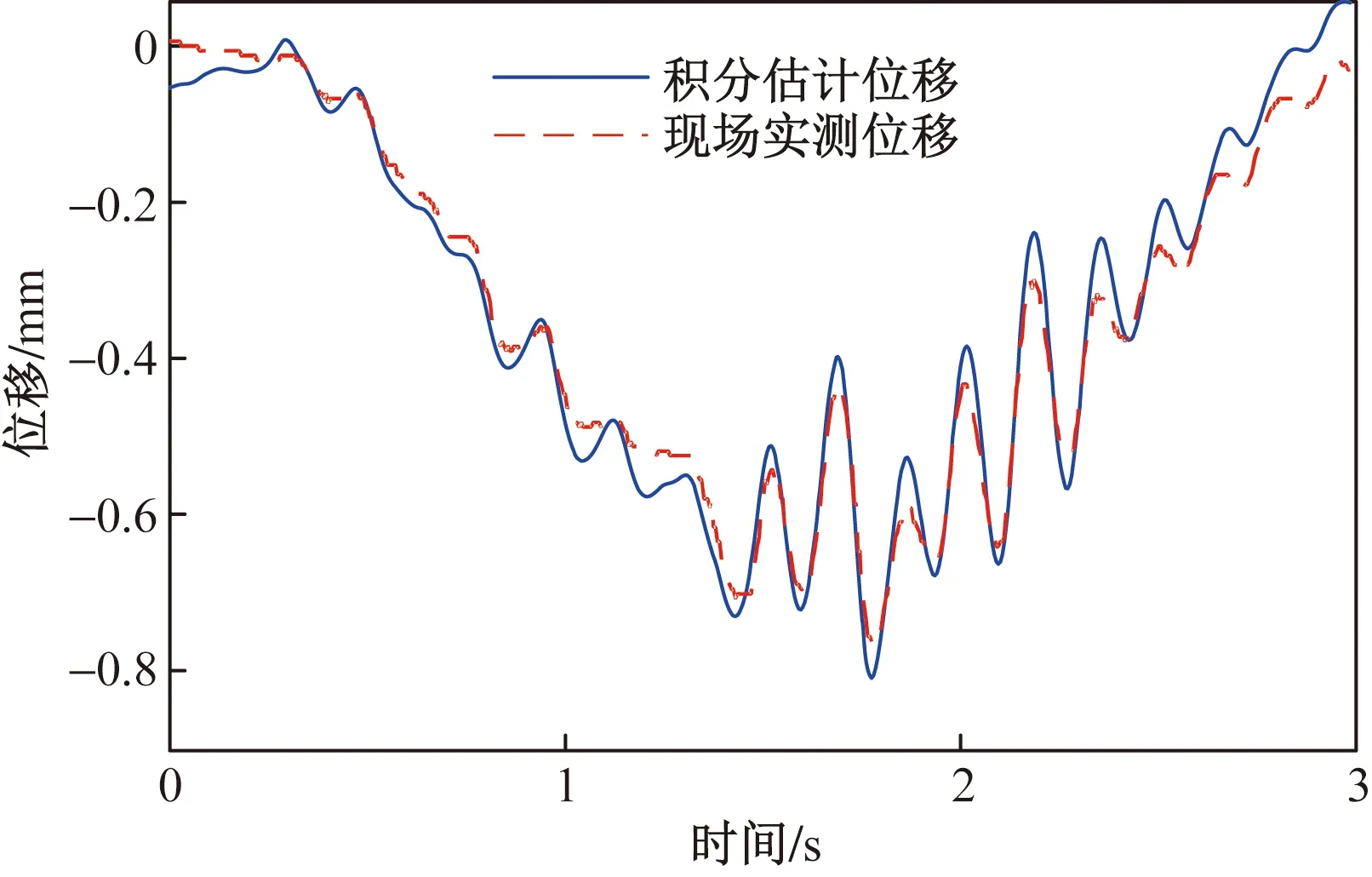
图11 车速30.4 km/h时实测位移与积分位移对比Fig.11 Comparison of estimated and direct measured displacement under moving vehicle with 30.4 km/h speed

2.3 试验结果分析

基于不同车速工况下实测加速度数据对试验中桥梁位移进行估计并与对应实测位移进行对比。图12给出了其他车速工况下的积分估计与实测动位移曲线的对比,结果表明二者的吻合度较好。

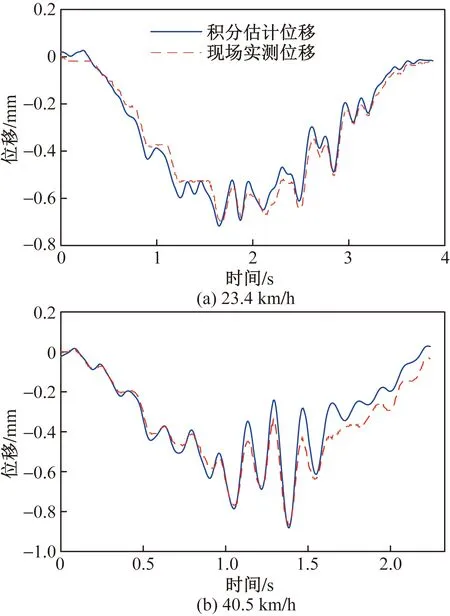
图12 其他车速下积分估计位移与现场实测位移的对比Fig.12 Comparison of estimated and direct measured displacement under moving vehicle with different speeds

为了评估此间接测量方法的准确性,构建相对峰值误差ζP和最大差值误差ζD两个指标对估计和实测位移时程曲线的吻合程度进行评估。

相对峰值误差公式为

(13)

式(13)中:dE为任意时刻桥梁加速度积分动位移;dM为任意时刻实测动位移。

最大差值误差公式为

(14)

式(14)中:σ(dE-dM)为估计值与实测值差值的标准差。

将所求评估指标列入表1。

通过积分估计动位移与实测动位移的曲线对比及误差分析发现,位移间接估计与实测值的峰值差值在0.015～0.041 mm,3个工况的平均值为0.026 mm;相对峰值误差在1.68%～5.29%,平均值为3.34%,说明积分所得位移准确度较好。同时,估计和实测位移的最大差值均小于3.4倍的差值标准差,说明两者吻合程度较好,且误差分布较为均匀。

3 结论

基于加速度估计位移既有理论,对时域积分原理和基线校正方法进行分析研究,提出联合实测加速度动静分离和最小二乘法基线校正的桥梁动位移间接测量方法。通过多种车速工况下的实桥试验验证了方法的精度和有效性。该方法操作简单,除布置加速度传感器外仅需记录汽车上桥与下桥时间,对不同桥型具有通用性。20 m跨度简支梁实桥试验表明所提方法估算得到位移与直接测量值吻合良好,多种车速工况下峰值相对误差低于5.29%,表明该方法具有较高的精度和实际应用价值。同时,试验验证依托桥例跨度较小,由此车载下位移响应幅值较低,导致相对误差增大。后继研究中,将针对不同跨度和桥型开展研究,进一步分析多种影响因素对方法适用性的影响,推动方法向应用发展。