超高速碰撞产生等离子体及电磁辐射效应的研究进展
巨圆圆, 张磊, 张庆明
(1.海军研究院, 北京 100161; 2.北京理工大学爆炸科学与技术国家重点实验室, 北京 100081)
超高速碰撞产生电磁辐射是固体物质在强冲击作用下的重要物理响应。通常,固体物质在受到超高速碰撞时,会发生断裂、破碎、成坑、成腔和出现粒子云的膨胀,随着碰撞速度的增大,会发生多形性固-固相变,还可能出现熔化现象,在更高碰撞速度下,还会出现气化,产生等离子体,并产生从低频到高频的电磁辐射,如微波和可见光等[1-3]。这种电磁辐射的形成过程非常复杂,与超高速碰撞的力学过程如变形、断裂、破碎、成坑、粒子云化、相变(包括多形性固-固相变、熔化、气化和等离子体化,也可说是物理过程)等紧密耦合在一起。一方面,这些力学过程直接关系到电磁场的产生、辐射的频谱特性;另一方面,碰撞产生的电磁场将影响其应力场,从而影响变形、断裂、破碎、成坑、粒子云化、相变等过程。超高速碰撞在天体碰撞领域、深空探测领域、航天器对空间碎片防护领域、军事领域(如空间毁伤方面)具有重要应用[4-6]。
目前为止,国内外学者在超高速碰撞产生等离子体及其电磁辐射效应方面已不断开展了大量的研究。现从实验研究、理论研究和计算机模拟3个方面分别予以介绍。
1 实验研究
1963年Frichtenicht和Slattery首次报道了超高速碰撞产生等离子体的现象[7]。通过实验手段观测到了等离子体信号,经过分析指出:等离子体信号的持续时间维持在微秒量级,在碰撞点处等离子体的电子密度很大,等离子体初始膨胀速度与其他喷出物的速度相近,其能量为几个电子伏,而在超过几十厘米的距离处,能量会变得很小。图1为超高速碰撞产生等离子体示意图。

图1 超高速碰撞产生等离子体示意图Fig.1 Schematic diagram of plasma produced by hypervelocity impact
超高速碰撞过程中,弹丸和靶板材料部分气化、电离产生等离子体,并向周围真空环境迅速膨胀[8-9]。大量实验结果表明,超高速碰撞产生的净电荷与碰撞体大小(质量)、碰撞速度有关[10-12]。在实验基础上得到了以下经验关系[9-12]。
Q∝mprojvimp
(1)
式(1)中:Q为净电荷,C;mproj为弹丸质量,kg;vimp为碰撞速度,km/s。
不同的研究者得到的指数值不尽相同。基于静电尘埃加速器实验,Dietzel等[9]得到α=0.9和β=2.7;利用相同的实验装置,McBride等[11]和Drolshagen[12]分别得到α=1.02和β=3.48;Ratcliff等[10]得到α=1和β=4.74。
Crawford等[13]在美国宇航局(National Aeronautics and Space Administration, NASA)实验室测量了超高速碰撞条件下膨胀等离子体的电导率,由于等离子体中包含离子、电子和中性粒子的不确定性,等离子体电导率是温度、压力、密度和电离度的复杂函数。实验表明弹丸以5.5 km/s的入射撞白云石靶板,可以使弹丸和靶板材料部分气化,产生等离子体。Hood等[14]预言电导率分布可用β近似,在高电离情况下,β=0;在部分电离情况下,β>0。
Crawford等[15-18]对超高速碰撞产生等离子体和电磁特性进行了实验研究。研究表明,超高速碰撞产生等离子体的电磁效应会干扰或毁伤卫星的电子设备;净电荷和碰撞体的质量呈线性关系,产生的电磁场和碰撞体的半径呈线性关系;超高速碰撞产生的电磁场和碰撞角度、碰撞速度以及弹靶材料相关。
Dugger等[19]给出了含有少量铝和镁的铝合金弹丸以5.5 km/s的速度碰撞与弹丸材料相同靶板的光谱辐射及光辐射强度,如图2、图3所示。
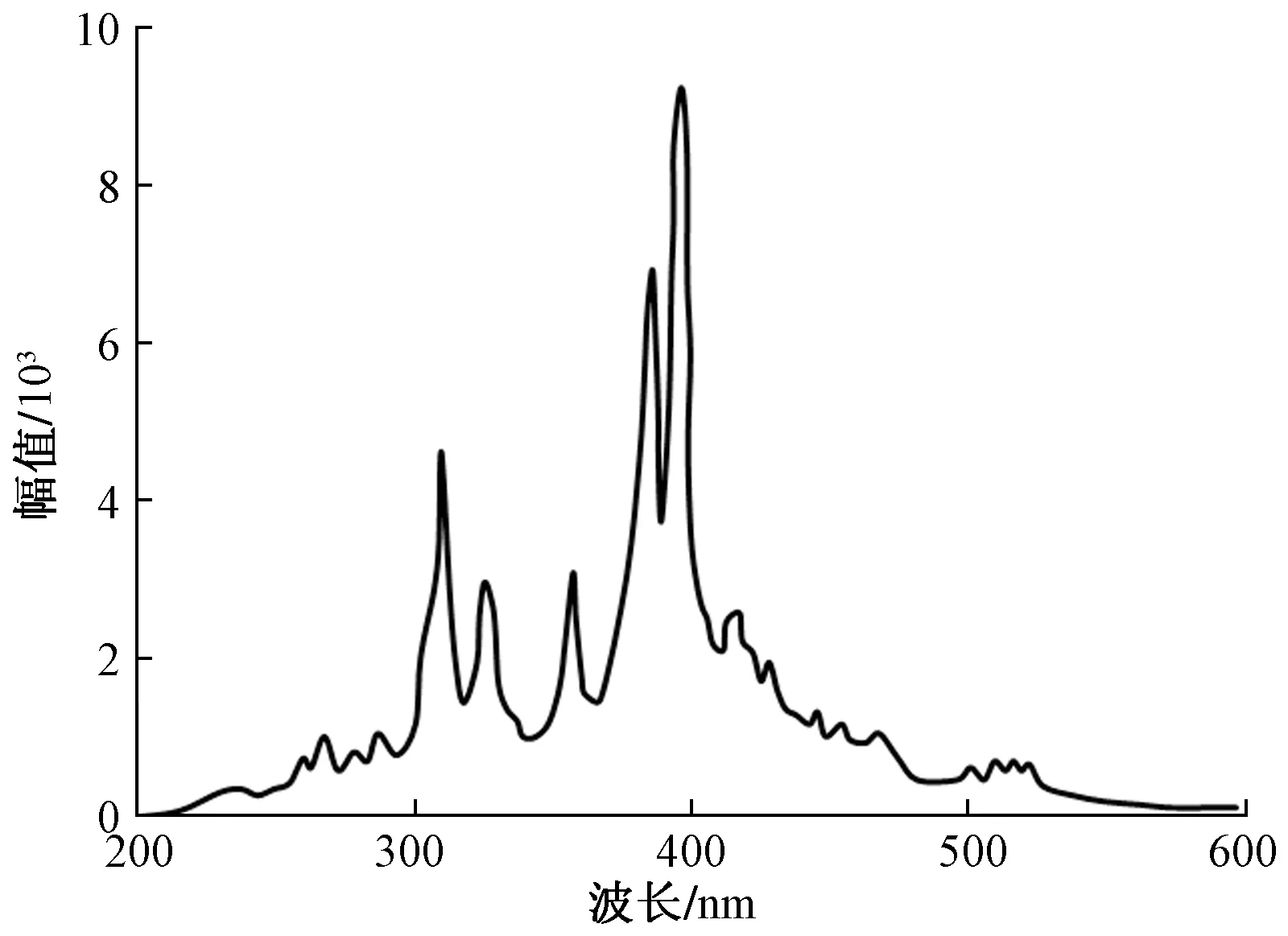
图2 超高速碰撞产生的光谱辐射[19]Fig.2 Spectral radiation induced by hypervelocity impact[19]

sr(球面度)表示立体角,1 sr=1 m2/m2=1图3 超高速碰撞产生的光辐射强度[19]Fig.3 Spectral radiation intensity of light induced by hypervelocity impact[19]
Kissel等[20]对超高速碰撞产生等离子体作用于航天器电子元器件的效应进行了研究,通过 DICAM-PRO分幅相机拍摄了碰撞闪光的实验照片。图4为弹丸以6.7 km/s撞击1.2 mm铝靶板得到的闪光图像。

图4 超高速碰撞产生的闪光现象[20]Fig.4 Flash of light induced by hypervelocity impact[20]
Ernst等[21]给出了超高速碰撞实验中的闪光强度信号。实验中弹丸材料为耐热玻璃,靶板材料为浮石,碰撞速度在4.05~6.14 km/s,碰撞角度在 30°~90°,实验结果如图5所示。可以看出,闪光曲线由两部分组成,首先出现闪光的强度峰值,该峰值的大小依赖于弹丸的材料性质和碰撞速度与角度;然后出现长时间的黑体衰减信号,该衰减信号的特征依赖于靶板的材料性质和实验参数。同时,还得到超高速碰撞的黑体衰减信号与时间存在关系式,并给出了实验中不同材料的α取值,如图6 所示。
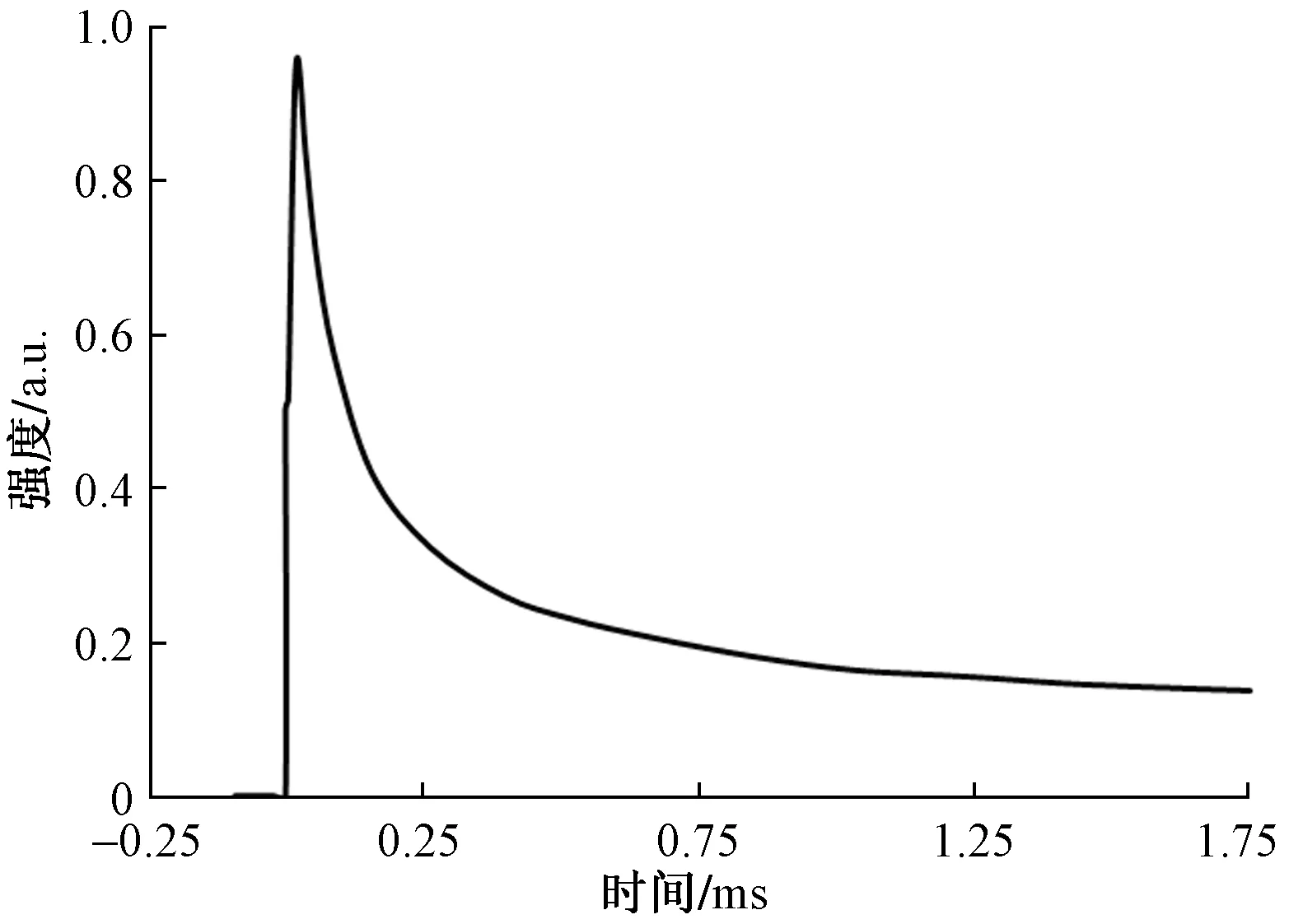
图5 闪光强度历史曲线[21]Fig.5 History of flash intensity[21]

图6 衰减曲线及衰减指数[21]Fig.6 Attenuation curve and its index[21]
Schultz等[22]给出了超高速碰撞产生闪光的总能量为

(2)
式(2)中:σ为Stephan-Boltzmann常数,5.67×10-8W/(m2·K4);T为色温;A为有效源面积;θ为碰撞角。碰撞闪光总能量LE和碰撞动能KE存在关系为
LE=ηKE
(3)
式(3)中:η为发光率,一般在10-6~10-5。
Lawrence等[23]给出了钛飞片以11.0 km/s碰撞铝板时的闪光强度,光辐波长和时间之间的三维关系图,如图7所示。可以看到,闪光强度随光辐波长和时间的变化趋势不尽相同。

Δt为弹丸碰撞靶板后的时间,碰撞瞬时t=0 μs图7 不同波长的闪光强度随时间变化的三维图[23]Fig.7 Three dimensional view of flash intensity at different wavelengths over time[23]
Harano等[24]对太阳能电池阵结构的超高速碰撞实验进行了研究,实验中采用郎缪尔探针对碰撞产生等离子体的电子温度和电子密度进行了测量,给出了一定碰撞速度下电子温度的量级,能达到几个电子伏。
文献[25-28]对超高速碰撞产生的微波辐射进行了大量实验研究。研究结果表明,微波辐射信号由正负脉冲信号和连续脉冲信号组成,碰撞速度、靶板材料和靶板厚度对微波辐射强度有很大影响。碰撞速度越大,微波辐射产生能量越大,且正比于碰撞速度的5.7次方(∝v5.7);导体材料靶板比绝缘体和半导体材料靶板受到超高速碰撞产生的微波辐射强度大;靶板越薄,碰撞过程中受到的毁伤程度越大,产生的微波辐射强度越大。图8为1 g聚碳酸酯弹丸以4 km/s的速度撞击铝靶板产生的微波辐射信号,图9~图11分别为靶板材料、碰撞速度和靶板厚度对微波辐射能量的影响。

图8 超高速碰撞产生的典型微波辐射信号[26]Fig.8 Typical microwave radiation from hypervelocity impact[26]

图9 靶板材料对微波辐射能量的影响[28]Fig.9 Effect of target material on microwave radiation energy[28]
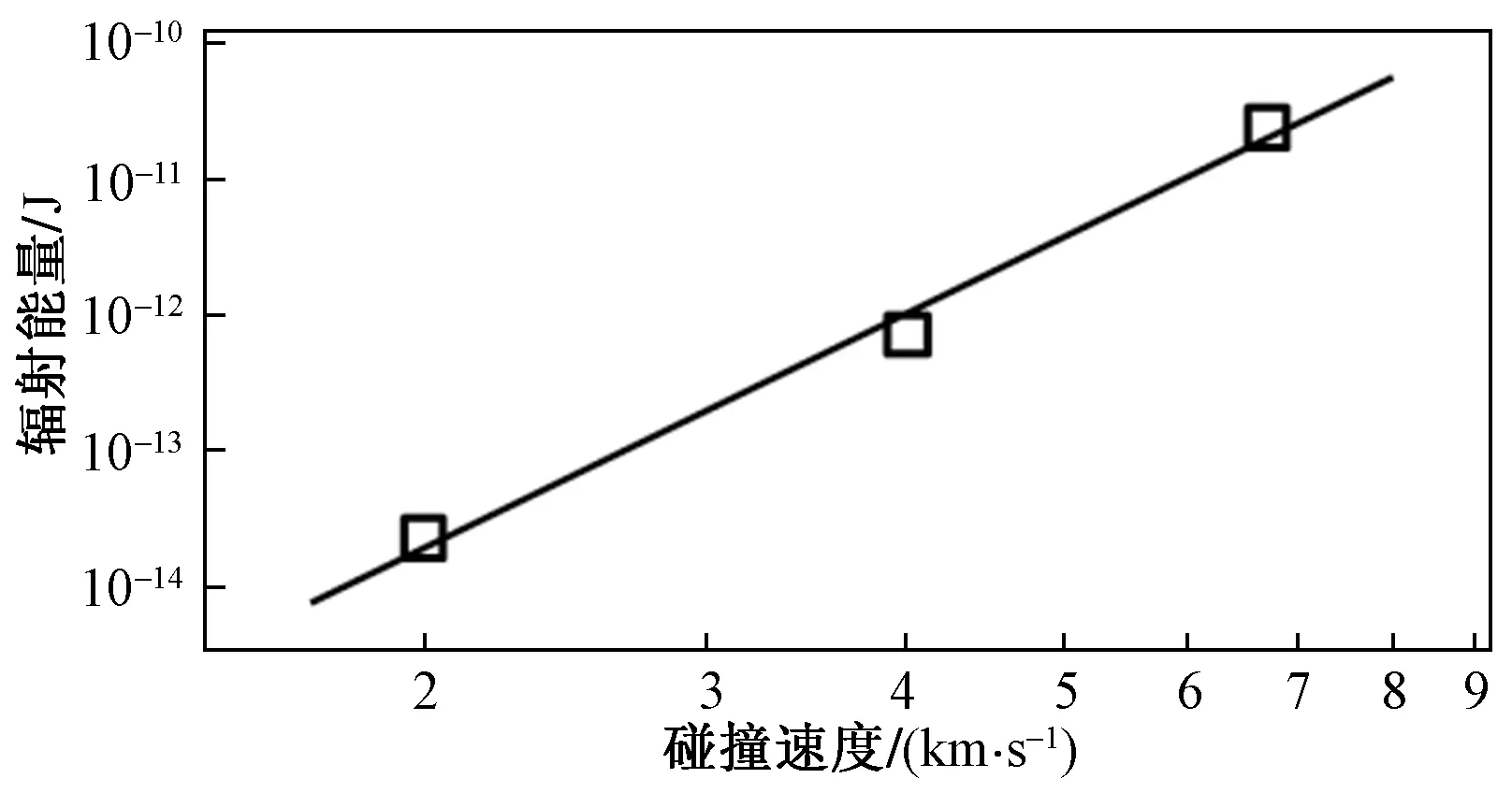
图10 碰撞速度对微波辐射能量的影响[28]Fig.10 Influence of impact velocity on microwave radiation energy[28]

图11 靶板厚度对微波辐射能量的影响[28]Fig.11 Effect of target thickness on microwave radiation energy[28]
Johnson等[29]、Lee等[30-31]利用Van de Graaff尘埃加速器对超高速碰撞产生等离子体的射频辐射进行了实验研究。质量为10-16~10-11g的铁弹丸以1~70 km/s的速度撞击不同材料和不同带电量的靶板,利用迟滞电压分析仪(retarding potential analyzers, RPAs)、光电倍增管、电场传感器等对超高速碰撞产生等离子体信号、闪光信号和电场信号进行了测试。结果表明,等离子体信号对靶板材料和靶板带电量依赖性较大,碰撞不带电靶板产生等离子体的膨胀速度大约为20 km/s。典型电场信号的去卷积可以用高斯函数描述,包括一个强脉冲和后续的展宽较大的脉冲。
中国学者对超高速碰撞产生等离子体及电磁辐射效应进行了初步研究。石安华等[32-33]、马平等[34]测量了直径为5 mm的铝合金(LY12)小球以1.98~4.30 km/s的速度垂直撞击材料为铝合金(LY12)和黄铜的半无限靶,得到了微波辐射强度随时间的变化以及微波辐射峰值的变化规律。实验发现,随着弹丸速度的增加,弹丸对同一靶材撞击产生的微波辐射强度明显增强,说明弹丸速度对微波辐射强度有较大影响;在弹丸速度相同情况下,撞击黄铜产生的微波辐射强度远大于撞击LY12铝产生的微波辐射强度,说明靶材对微波辐射强度也有一定影响。同时,还测量了LY12铝和黄铜靶在超高速碰撞下不同波长的闪光强度。
唐恩凌等[35-38]、马月芬等[39-40]对超高速碰撞产生等离子体及电磁辐射效应进行了实验研究。初步获得了超高速碰撞铝靶产生等离子体的临界条件、碰撞速度和碰撞角度对超高速碰撞产生等离子体的影响、等离子体时空分布规律;碰撞速度和碰撞角度对闪光强度的影响。图12、图13分别为直径6.4 mm的LY12铝球以5.35~5.97 km/s的速度在不同碰撞角度下撞击LY12铝板产生的等离子体平均电子温度和闪光强度。另外,采用磁线圈测量了铝弹丸以6 km/s左右的速度撞击铝靶产生的电磁场强度以及该电磁场对电子电路的干扰,如图14所示。实验结果表明超高速碰撞产生的电磁场最大幅值在15 μT,持续时间为1 ms左右。

图12 不同碰撞角度下等离子体平均电子温度[38]Fig.12 Average electron temperature of plasma at different impact angles[38]

图13 单峰型闪光强度[35]Fig.13 Single-peak flash intensity[35]

图14 超高速碰撞产生磁场及其对电路信号的干扰[40]Fig.14 Hypervelocity impact generated magnetic field and disturbance onto circuit signals[40]
2 理论研究
Srnka[41]认为在超高速碰撞产生等离子体初期存在热驱动的电流和诱发磁场。碰撞过程中碰撞点附近的温度和密度梯度驱动等离子体中带电粒子运动,由此发展了超高速碰撞产生磁场的简单模型。该模型基于等离子体法拉第电磁感应定律和广义欧姆定律,描述了磁感应强度随时间的变化率,公式为
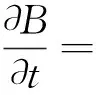
(4)
式(4)中:B为磁场强度;u为等离子体膨胀速度;μ、σ分别为等离子体磁导率和电导率;α为张量系数;kB为玻尔兹曼常数;n、T和e分别为电子密度、电子温度和电子电荷;符号×表示向量叉积。
Pert[42]从理论上深入分析了超高速碰撞产生等离子体的内部磁场,等离子体内部磁场演化的微分方程为


(5)
式(5)中:等号右边三项分别为层流项、扩散项和源项。
电子能量密度εe由微分方程式(6)给出,即

(6)
式(6)中:Qt为热流。
电子比能W由式(7)给出,即

(7)

(8)

(9)
式(8)和式(9)是关于电子能量和磁场演化的偏微分方程,只有电子回转半径比典型的等离子体尺度更大时才有效。在早期阶段磁场很弱,电子回转半径很大,等离子体运动受磁场的影响不大。随着磁场的增强,对等离子体运动速度的影响也会越来越大。最后,磁场增强停止,这时磁场梯度与电子压力梯度达到平衡,磁场的能量密度与等离子体的能量密度相当。
Lee等[43-44]在实验基础上提出了一种等离子体膨胀模型。他们将等离子体运动分为4个阶段来描述:动力学理论(kinetic theory)、磁流体(magnetohydrodynamics, MHD)、流体描述和单粒子运动(single particle motion, SPM)。超高速碰撞产生等离子体初期,其密度很高而体积很小,还没有达到热平衡,可以用动力学理论描述;等离子体形成之后剧烈振荡迅速达到热平衡,可以用流体理论描述;当等离子体膨胀到一定程度,粒子之间的相互作用非常小时,可以用单粒子运动描述。
等离子体形成之后迅速达到热平衡状态,其运动方程为

mng-∇·P+mnvv
(10)
式(10)中:m为粒子质量;n为粒子数密度;q为粒子电荷;v为粒子速度;E为电场;B为外部磁场;g为重力加速度;P为压力张量;ν为粒子碰撞频率。
式(10)等号右边四项在等离子体膨胀过程中的重要性极为不同。外部磁场和重力可以忽略,等离子体压力和等离子体振荡起主要作用。由于等离子体很快达到平衡,速度满足等温、各向同性的Maxwell分布,可以看作是理想气体,因此有
∇·P=∇(nkBT)=kBT∇n
(11)
式(11)中:kB为波尔兹曼常数;T为等离子体温度。
当德拜长度小于等离子体半径时,外部电场对等离子体运动没有影响,等离子体以热速度膨胀,该速度描述了等离子体中的粒子速度分布,公式为

(12)
式(12)中:vth,i为等离子体速度分布;Ti为等离子体温度分布。
在这种情况下,里根在1981年总统就职演说中强调:“在目前的危机中,政府不能解决问题,政府本身就是问题”,从而拉开美国社会保障改革的序幕。同一年,里根开始了他的“经济复兴计划”。这份计划概括地讲就是“三砍一稳”,即大砍联邦预算开支,大砍个人与企业的税率,大砍政府下达给企业的各种规章条例,以及要求制定一项稳定的货币政策[4]176。
等离子体频率为

(13)
式(13)中:ωp,e为等离子体振荡频率;ne为等离子体电子密度;ε0为介电常数。
除了等离子体振荡产生射频辐射外,等离子体膨胀运动使其密度和振荡频率降低,也会产生电磁辐射。随着等离子体的膨胀,德拜长度超过等离子体半径,外部电场使等离子体内部正负粒子分离,形成电流脉冲进而产生射频辐射。此时,等离子体内部粒子之间的相互作用变得很弱,只受到外部电场的作用,可以用单粒子运动描述。
假设等离子体受到均匀的外部电场作用,粒子运动方程为
F=qEext
(14)
式(14)中:F为等离子体受到的外部电场作用力;q为粒子电荷量;Eext为外界电场强度。
定义粒子初始速度为
(15)
式(15)中:v0为粒子初始速度;d为粒子在电场中运动长度;t为粒子在电场中运动时间;m为粒子质量。
假设靶板带正电荷,相应的外部电场方向沿靶板法向,等离子体中带正电荷的粒子将会加速运动远离靶板表面,反之亦然。给定等离子体中的粒子一个初始速度分布,每一个粒子随时间运动,将会产生一个电流脉冲。通过电流脉冲宽度可以得知等离子体速度分布,进而得到等离子体温度。
等离子体中粒子初始速度概率密度为

(16)
式(16)中:ηi为粒子i的电荷分数;Q为总电荷量。
电流脉冲为
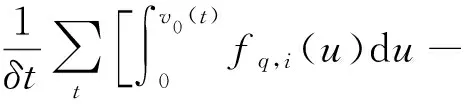

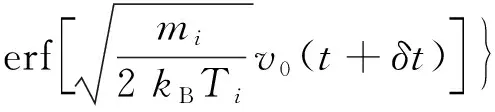
(17)
式(17)中:erf为误差函数。
弹丸超高速正碰撞靶板,在碰撞点周围会形成一个半球形弹坑,部分弹丸材料和靶板材料向外飞溅形成碎片云,同时,一小部分发生气化和电离,形成等离子体。等离子体初始密度很大,由大量带电粒子和中性粒子组成,迅速达到热力学平衡状态,其内部温度均匀,因此,发生电离的自由电子运动速度远大于带正电的粒子和中性粒子的运动速度,从而产生分离电荷,分离电荷积累会产生电场,电场会抑制自由电子的膨胀运动,因此,在一定区域内自由电子会发生振荡,并因而产生电磁脉冲向周围空间辐射。Close等[45-47]、Kelley等[48]、Janches等[49]通过估计净电荷和等离子体温度、电离度、膨胀速度,建立等离子体膨胀模型和电磁脉冲机制,并且和碰撞Cassini宇宙飞船上仪器的数据吻合很好。
超高速膨胀产生的净电荷Q可利用经验公式[12]进行估计,即

(18)
式(18)中:m为弹丸质量,kg;v为碰撞速度,km/s。
超高速碰撞产生的弹坑可以利用经验公式[50]估计,即
r0=km0.352ρ0.167v0.667
(19)
式(19)中:ρ为弹丸密度,g/cm3;k为经验系数,对铝k=0.42。
弹丸超高速碰撞靶板,在靶板中产生一个半球形弹坑,部分弹丸和靶板材料发生电离,形成等离子体,由式(12)和式(13)估计等离子体初始电子密度ne,0。等离子体形成之后迅速达到热平衡状态,其电子温度和其他粒子温度相同,并假设在等离子体膨胀过程中温度不发生变化,和外界没有能量交换。等离子体的电子温度为Te~v1.4[51],电离度为1%[52]。假设净电荷球形对称分布在等离子体表面,等离子体膨胀速度近似为粒子的等温声速,因此,电子密度随时间变化关系为

(20)

图15 等离子体密度变化曲线[45]Fig.15 Plasma density curve[45]


(21)
运动方程的WKB近似解(如图16所示)为

图16 等离子体膨胀运动历史[46]Fig.16 History of plasma expansion motion[46]


(22)
辐射功率可由Larmor公式计算(如图17所示),公式为

(23)
式(23)中:c为光速;N为等离子体中的电子数。
文献[53-55]在对实验结果分析的基础上,研究了超高速碰撞产生微波辐射的物理机制,提出了超高速碰撞微波辐射的微裂纹放电模型。当弹丸超高速碰撞靶板时,靶板中形成弹坑,其表面出现大量微裂纹。由于化学键的断裂或压电效应引起微裂纹表面的电荷分离,形成瞬时电流,并以一定的角频率振荡,向周围空间辐射电磁波。用电偶极子来描述分离电荷,在碰撞点附近产生的电场强度和辐射功率可以由下述方法计算,图18为微波辐射微裂纹放电模型的示意图。

图18 微波辐射模型[55]Fig.18 Microwave radiation model[55]
电子激发过程可以用Richardson-Dushan方程来描述为

(24)
式(24)中:A为常数;T为温度;φ为功函数;kB为波尔兹曼常数。

(25)
式(25)中:τ为瞬时响应时间;ω为测量频率(电流振荡频率)。
电场强度可以表示为

(26)
式(26)中:I为电流强度;l为裂纹宽度;c为光速;ε0为真空介电常数;r为碰撞点离测点的距离。
单个裂纹辐射功率为

(27)
式(27)中:Gr为接收天线增益;λ为波长。
由式(18)~式(21)可以得到总的辐射功率和功函数的关系(如图19所示)。

T为温度;n为微裂纹数图19 微波辐射能量和功函数关系[53]Fig.19 Relation between microwave radiation energy and work function[53]

(28)
式(28)中:K为常数;n为微裂纹数。
在实验基础上还提出了其他模型,比如弹性能模型。该模型认为在弹丸侵彻靶板过程中,作用于靶板的力F不变。弹性能W定义为

(29)
式(29)中:l为靶板厚度;E为靶板弹性模量。
微波辐射能量和弹性能有一定关系,弹性能和超高速碰撞产生的微裂纹数有关,即和靶板破坏程度相关,所以超高速碰撞产生微波辐射能量和靶板破坏程度相关。图20为计算得到的微波辐射能量和弹性能的关系。

图20 微波辐射能和弹性能关系[53]Fig.20 Relation between microwave radiation energy and elastic energy[53]
3 计算机模拟
目前,国内外对超高速碰撞产生等离子体电磁辐射的实验研究和理论研究相对较多,数值模拟研究几乎没有。近年来,各国学者利用分子动力学方法在原子层次上对超高速碰撞现象进行了大量研究,但主要集中在变形机制和冲击相变的研究方面[56-63]。图21为单晶铝超高速碰撞条件下的冲击Hugoniot曲线。

HLP为Harrison局部赝势;MD为分子动力学图21 单晶铝冲击熔化曲线[57]Fig.21 Shock melting curve of single crystal aluminum[57]
2011年加州理工学院提出了一种新的分子动力学方法——电子力场[64-67]。电子力场本质上是一种分子动力学模拟方法,它是量子力学和经典分子动力学的结合,能够显式地计算含有电子的体系,能够在时间尺度为皮秒、空间尺度为 104个原子上描述激发态电子动力学。但是,电子力场假设单电子可以用球形高斯波函数来描述,所以只能处理包含s电子的体系。图22为利用电子力场方法计算得到的金属锂等离子体相变图像。图22(a)为锂板以速度Up撞击活塞壁后,冲击波以速度Us向右传播的侧视图,并用颜色编码的电子描绘了压缩区域中的一部分的电离电子(朝向红色)和一小部分较高动能局域电子(朝向蓝色);图22(b)为图22(a)中相同时刻的活塞壁的前视图;图22(c)中0~4的颜色梯度表示原子核与电离电子之间的电子半径,蓝色表示原子核,红色表示电离的电子。

ρ0为压缩前介质密度;ρ1为压缩后介质密度;Us为冲击波速度;Up活塞速度;P0、V0、E0分别为压缩前介质压力、体积、内能;P、V、E分别为压缩后介质压力、体积、内能图22 冲击波引起锂原子电离[65]Fig.22 Ionized lithium atoms induced by shock wave[65]
为了描述更加广泛的元素,在电子力场基础上,引入有效核赝势(effective core pseudo-potentials, ECP)的概念,使电子力场能够描述包含p电子和d电子体系的电子动力学特性[68-70]。它的主要思想是将含有多个电子的金属原子进行简化,使其包含的电子数量显著减少,建立含有拟定参数的赝势来描述核电子和价电子之间的泡利排斥能,从而可以对含有p电子和d电子的体系进行快速求解。图23 为利用有效核赝势方法计算得到的硅脆性断裂过程中沿裂纹轨迹的电离电子数量。

图23 硅脆性断裂裂纹方向电离电子数量[71]Fig.23 Number of ionized electrons in the direction of silicon brittle fracture crack[71]
因此,基于有效核赝势思想的电子力场方法能够模拟超高速碰撞条件下金属铝的电子动力学行为,为研究超高速碰撞产生等离子体的电磁效应提供了一种新的方法。
4 结论与展望
国内外学者通过实验和理论研究已在超高速碰撞产生等离子体及电磁辐射效应方面取得了一定进展,初步建立了等离子体膨胀和电磁辐射模型,得到了碰撞参数、弹靶材料特性影响等离子体及电磁辐射效应的初步结论。通过电子力场方法和第一性原理对超高速碰撞产生的等离子体相变进行了初步探索,为从微观上揭示超高速碰撞产生等离子体的机理提供了一种崭新途径。但是,仍然有很多问题需要尽快深入研究。如:超高速碰撞产生等离子体和电磁辐射效应之间存在什么样的关系?超高速碰撞产生电磁辐射效应的机理是什么?电磁辐射的强度特性与碰撞参数之间有什么关系?电磁辐射特性与力学效应有什么关联?因此,从微观角度对超高速碰撞产生等离子体的电磁效应进行研究,结合已有实验结果,建立超高速碰撞产生等离子体的电磁效应的数学物理模型,对于揭示超高速碰撞电磁辐射机理、电磁辐射强度与碰撞参数之间的关系以及电磁辐射与力学耦合效应都具有十分重要的意义。

