基于完全集成经验模态分解和模糊熵分频的短期风电功率预测
文博, 陈芳芳, 胡道波, 罗银榕, 张倩倩
(云南民族大学电气信息工程学院, 昆明 650031)
中国制定了相应的“碳达峰”合“碳中和”计划,将力争于2030年前二氧化碳排放达到峰值,努力争取在2060年前实现碳中和。因此,风能、太阳能、地热能、核能等新能源的发展成了主要趋势。其中,风电在中国新能源电力中占有较大比例,且其因清洁环保、成本较低等优点成为新能源发展的主力。截至2021年7月底,中国非化石能源发电装机容量10.3亿kW,其中风电装机容量2.9亿kW[1-2]。但是,风力的波动性和随机性较大,易受天气因素的影响,给风电的利用率带来了较大限制。因此,短期风电功率的准确预测对电力系统稳定运行具有重要意义。
短期风电功率的预测方法主要可以分为物理方法、统计方法和组合预测方法三大类。物理方法对历史气象数据的精确性要求极高且模型与求解过程复杂,适应于某一特定地区的风电功率预测;统计预测法模型结构简单、计算速度较快,可以通过大量的历史数据可得到较好的预测结果,但是其预测精度随着时间序列的增加而迅速降低;组合预测方法采用其他方法对模型的输入、输出以及模型自身中的一种或者多种进行了优化并融合改进[3],具有强大的非线性映射功能,因此组合预测法是一种现在较为广泛的研究趋势。
文献[4]中采用变分模态分解(variational mode decomposition,VMD)分解将原始序列分解为N个中心频率不同的子序列,再用频率游程判别法将各子序列分为高频和低频分量,然后分别采用t-SSA-LSTM和t-SSA-ARIMA组合预测法对高频与低频分量进行预测,以此提高功率预测精度。文献[5]用完全集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)对原始风电功率序列进行分解,然后用精细复合多尺度熵(refined composite multi-scale entropy,RCMSE)对子序列进行重构,得到频率类别较为规律的序列分量。随后用基于哈里斯鹰改进的算法对极限学习机模型(extreme learning machine,ELM)进行优化,来提升预测精度,并引入AdaBoost来进一步提高预测精度。文献[6]用CEEMDAN对风电功率历史序列进行分解,再利用样本熵(sample entropy,SE)对所得序列分量进行重组,然后用模型堆叠(stacking模型)方法来构建预测模型,并用信息融合将历史功率序列与历史测风塔数据进行融合,以此构建高精度预测模型。
文献[7]提出了一种CEEMDAN和时间模式注意力机制改进的时间卷积网络模型,这也是一种分解-预测-重构的组合预测模型,首先用 CEEMDAN 对风电功率原始序列进行分解,然后使用该组合模型对各分量进行预测。文献[8]提出了一种RR-VMD-LSTM模型,首先使用鲁棒回归(robust regression, RR)和VMD对原始数据进行预处理,达到通过数据处理首先提高预测精度的效果,然后将处理过后的分解序列逐一输入到长短时记忆模型中分别进行预测。文献[9]将预处理后的信号用CEEMDAN分解,用辛几何模态分解(symplectic geometry mode decomposition,SGMD)对CEEMDAN分解后的最高频分量IMF1进行再分解。随后用粒子群算法对BiGRU网络进行优化,以此提高预测模型精度。但是,对原始序列分解之后,分解所得的子序列之和与原始序列之间存在较大的残差,重构后的序列可能存在模态混叠和频率混叠的情况。除此之外,传统的神经预测网络并没有对分解后的序列中的高频项和趋势项给予相应的关注。
针对上述问题,现建立一种基于模糊熵分频和CEEMDAN分解的短期风电功率预测模型。首先,利用CEEMDAN将原始风电功率分解为若干IMFs分量。随后采用模糊熵算法识别子序列的频率特征,并根据此特征将其分为高、中频分量和残差分量。分别建立SSA-LSTM-Attention和SSA-SVR模型来预测高、中频分量和趋势项。趋势项的频率低,振幅低,能反映一般外界对风力发电的影响,该项也会引起风电功率长期稳定的趋势变化。最后,叠加所有模型的预测结果得到风电功率预测值。并与其他模型对比以验证所提预测方法的优越性。
1 风电功率数据的分解与重构
1.1 CEEMDAN分解算法
经验模态分解(empirical mode decomposition,EMD) 是Huang等[10]针对信号的非线性、非平稳特点提出的一种自适应信号处理方法。根据数据本身特征对信号进行直接分解无须设置其他的基函数。EMD分解存在模态混叠现象,集合经验模态分解(ensemble empirical mode decomposition,EEMD)可以克服EMD的模态混叠问题,EEMD是一种噪声辅助数据分析方法。EEMD 在进行信号分解后可得到包括反映原始序列波动性的高频信号和反映其稳定性的低频残差信号。 由于残余噪声信号和加噪声信号不同,以此来实现的重构信号可能会导致产生的 IMF数量不同。虽然其整个过程能够有效地克服 EMD 方法的模态混叠缺陷,但并不能有效消除白噪声信号,所以使得重构误差过大。
CEEMDAN较 EEMD 而言分解速度更快且运算量也大幅减小。与CEEMD最后总体平均不同的是,它在得到第一次的IMF后就进行平均计算,这种处理方法有效地避免了白噪声信号从高频到低频的传递,从而影响最后的分析和处理。在接下来的每一个阶段都加入有限次的白噪声信号,能有效降低EEMD的重构误差[11],但也在一定程度上增加了运算量。其具体分解流程如下。
步骤1对风电功率原始序列C(t)添加白噪声,公式为
Cj(t)=C(t)+βknj(t)
(1)
式(1)中:t为原始功率分解的次数;Cj(t)为最新得到的功率序列;βk为第k个信噪比;nj(t)为第j次添加的高斯白噪声。
步骤2用原始功率序列计算残差信号。公式为
R1(t)=C(t)-imf1(t)
(2)
步骤3在R1(t)中加入正负成对的高斯白噪声,并对所得新信号R1(t)+β1E1[nj(t)]进行N次重复分解并求均值。由式(3)和式(4)得到分解后的第二个模态分量imf2及第二个残差信号R2(t)分别为
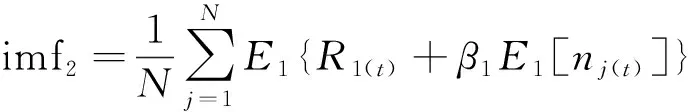
(3)
R2(t)=R1(t)-imf2
(4)
步骤4接下来不断地重复步骤3的计算过程,通过CEEMDAN不断地分解得到第k+1个模态分量imfk+1和第k个余量信号Rk。
步骤5重复上述步骤,最后得到若干个IMFs分量并计算出相应的满足条件残差分量。最终信号被分解为
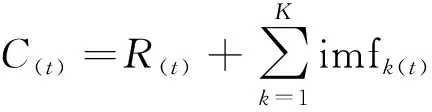
(5)
1.2 模糊熵
熵可以衡量时间序列的无序性。Shannon首次将熵引入信息论,提出了信息熵的概念来度量事件的不确定性。随后不同的熵方法被提出用于分析复杂性特征,包括量化金融市场效率[12]。由于模态之间的边界是模糊的,模态之间的关系也难以确定,为此提出了基于模糊理论的模糊熵方法,利用隶属函数计算不同隐藏模式之间的模糊相似度。具体而言,对于给定的时间序列x(t),t=1, 2,…,T,其中T为x(t)的长度,其模糊熵值计算如下。
步骤1基于时间序列x(t)构造嵌入向量X(i),嵌入维度为m,表达式为
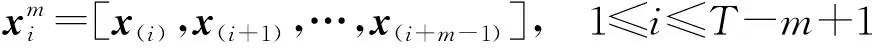
(6)

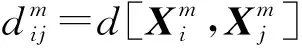
[x(j+k)-x0(j)]|}
(7)

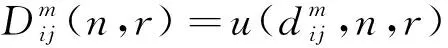
(8)
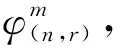
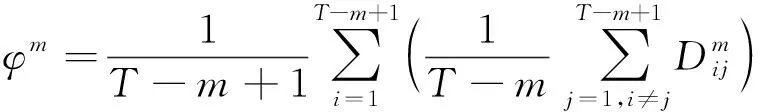
(9)

(10)
步骤5基于式(11)计算时间序列x(t)的模糊熵值。
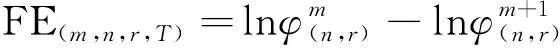
(11)
从式(11)可以看出,模糊熵值FE受参数m、n、r、T影响。其中m为嵌入维度,参数n、r决定模糊相似边界,T为样本长度。参考文献[13],嵌入维度m通常取2或3;而参数r设置不宜过大,否则容易丢失过多统计信息,因此,r一般取0.1σsd~0.25σsd,其中σsd为原序列的标准差;n取2或3。
2 风电功率预测模型构建
经过CEEMDAN分解后的原始数据大大降低了数据本身的复杂程度,将分解所得序列分为高频分量、中频分量以及趋势项。为了更准确地对各分量进行预测,搭建了长短期记忆网络(long short-term memory, LSTM)预测模型和支持向量回归(support vector regression,SVR)预测模型,分别对不同类型分量进行预测。在此过程中,为了更好地发挥预测模型的性能,选用麻雀算法(sparrow search algorithm,SSA)对模型进行优化,且为了区分不同分量信息的重要性,采用了注意力机制,以此达到优化模型性能、提高预测精度的目的。
2.1 LSTM原理
针对 RNN 网络出现的梯度消失和爆炸问题, Hochreiter等[14]提出一种长短期记忆网络(LSTM)。LSTM与 RNN 不同之处在于LSTM隐藏层内的循环递归单元中存在特殊的门控机制,有效地克服了梯度爆炸等问题[15-16]。一个LSTM模型有输入门、遗忘门和输出门[17]。LSTM非常适合处理和预测短期或者超短期内具有未知持续时间的时间序列,从而使其能够得到充分训练并且能展现出比RNN更加优异的性能。
LSTM网络采用反向误差传播算法对时间网络进行训练[18]。LSTM可以较好地对风速、风向、大气密度等相关时间序列进行预测,起到提高预测精度的效果,预测结果精度提高后更有利于进行相关的风电并网调度等一系列工作, LSTM的网络结构图[19]如图1所示。
LSTM中如遗忘门ft、输入门it、输出门ot等各变量可根据如式(6)~式(11)计算得出。
ft=σ(Wf[ht-1]+bf)
(12)
it=σ(Wi[ht-1,xt]+bi)
(13)
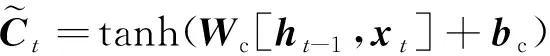
(14)
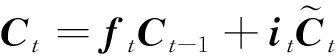
(15)
ot=σ(Wo[ht-1,xt]+bo)
(16)
ht=ottanhCt
(17)
式中:ht-1和ht分别为上一时刻和当前时刻的输出;xt为当前时刻的输入;Wf、Wi、Wc、Wo为各状态下的权重矩阵;bf、bi、bc、bo分别为各门偏置项向量;Ct-1和Ct分别为上一时刻和更新后的细胞状态向量。
2.2 SVR原理
支持向量回归(SVR)是由Vapnik[20]提出的一项数据挖掘技术,其以统计学理论为基础,基于VC维(Vapnik-Chervonenkis dimension)理论和结构风险最小化原理。SVR的基本思想是将影响因素映射到一个高维的特征空间。SVR具有出色的泛化能力,且对异常值具有鲁棒性,因此具有很高的预测精度。但是当数据集中有更多噪声时,SVR往往表现不佳,且其不适用于大型的数据集。鉴于SVR这些特点,将其用于对CEEMDAN分解后的趋势项进行预测,使得整体精度进一步提高。
SVR中非线性模型转化为一个高维的线性回归模型,表达式为
f(x)=ωTφ(x)+b
(18)
式(18)中:ω和b为模型参数。
由结构风险最小化原则,得到风险函数为
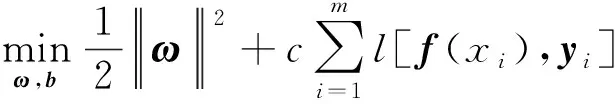
(19)
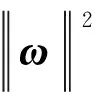
风险函数的最小值计算公式为

(20)

(21)
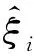
高维特征空间中内积运算可用核函数进行,为方便计算引入拉格朗日函数,将上述问题转化为对偶问题,可得非线性函数为
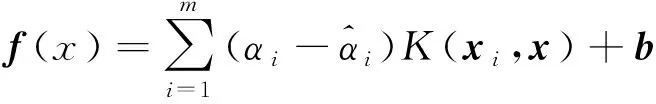
(22)

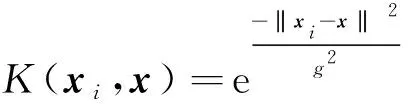
(23)
式(23)中:g为径向基核函数宽度。
2.3 SSA优化算法
麻雀搜索算法(SSA)[21]是于2020年提出的一种关于麻雀在觅食过程中各种行为的智能优化算法。麻雀是一种动作迅速的、记忆力好的群居动物,因此麻雀种群在觅食过程中具有一些更为显著的生物学特征,通过模仿麻雀的具体行为来获得最优值。
由麻雀的相关生物特征可概括为如下SSA的数学模型,在进行优化计算之前,必须将参数进行初始化,其中的参数包括种群大小、生产者数量、侦查员数量、最大迭代次数、搜索空间的维度以及搜索范围的上界和下界。随机生成的麻雀定义为xn,适应度函数用f(xi)表示。首先一个种群中n只寻找食物的麻雀可表示为

(24)
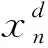
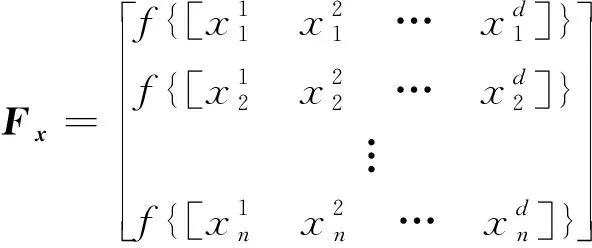
(25)
式(25)中:f为适应度值。
在SSA中,发现者的位置更新式为
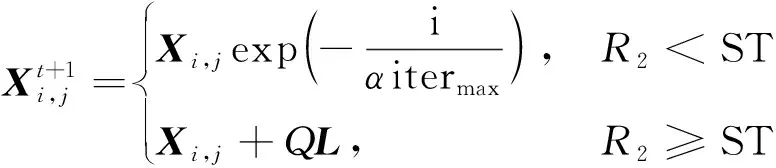
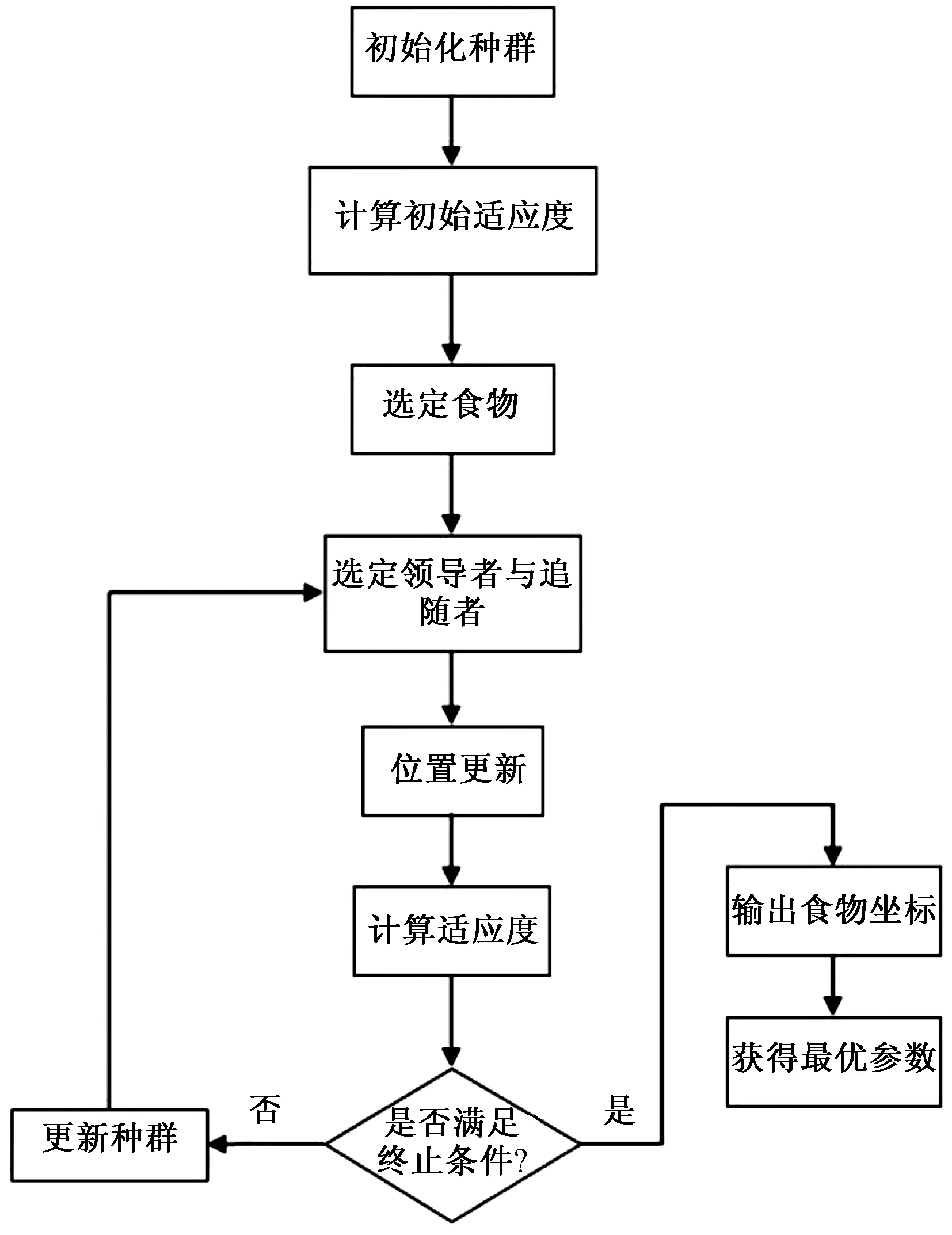
(26)
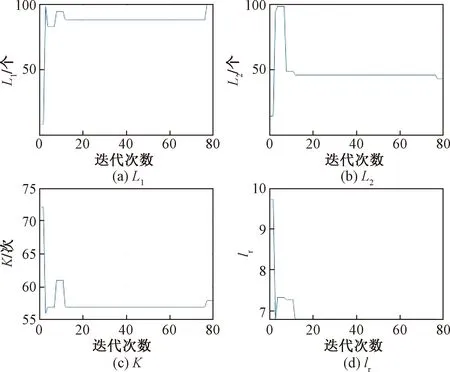
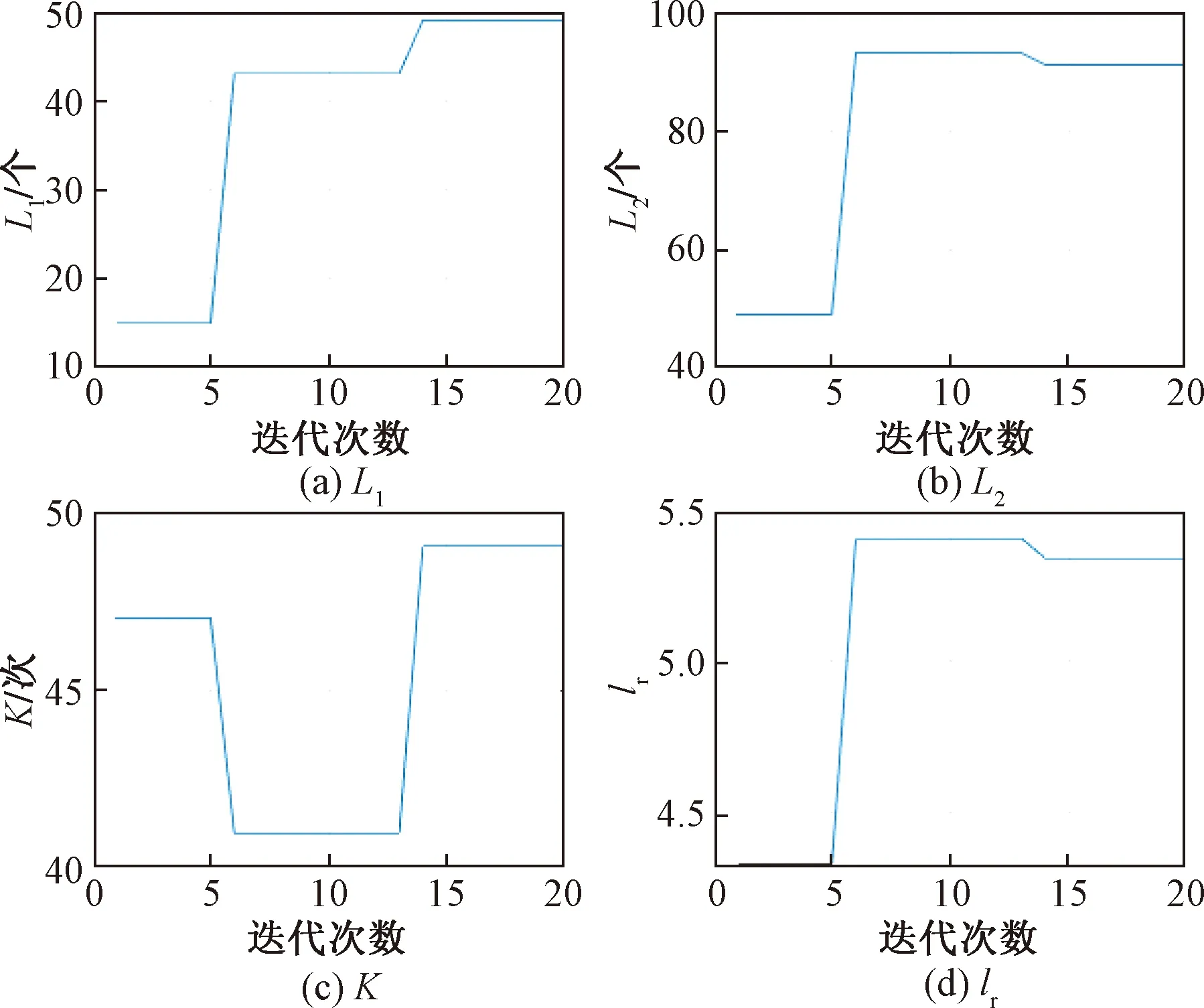
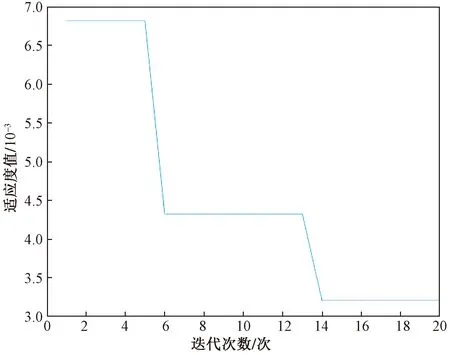
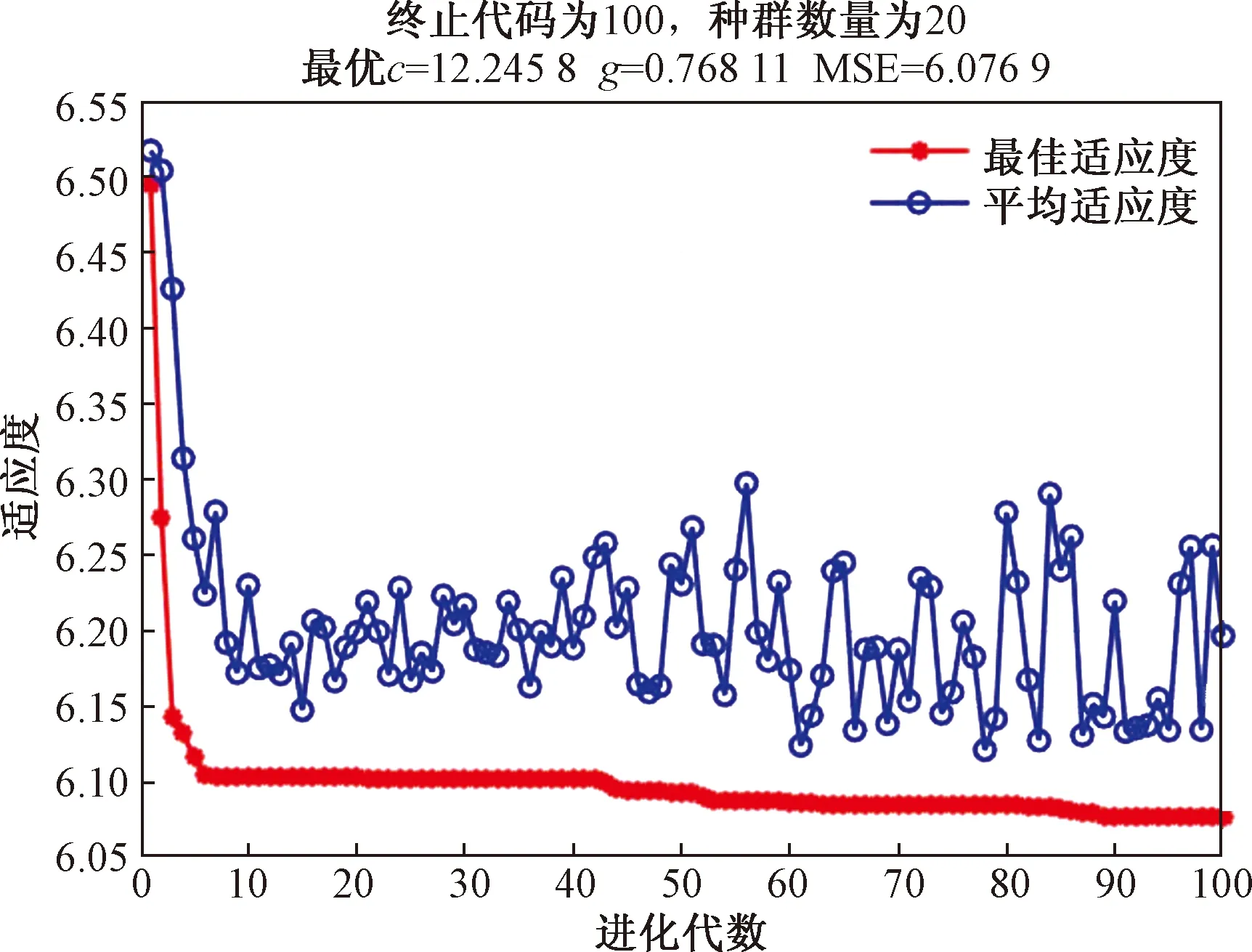
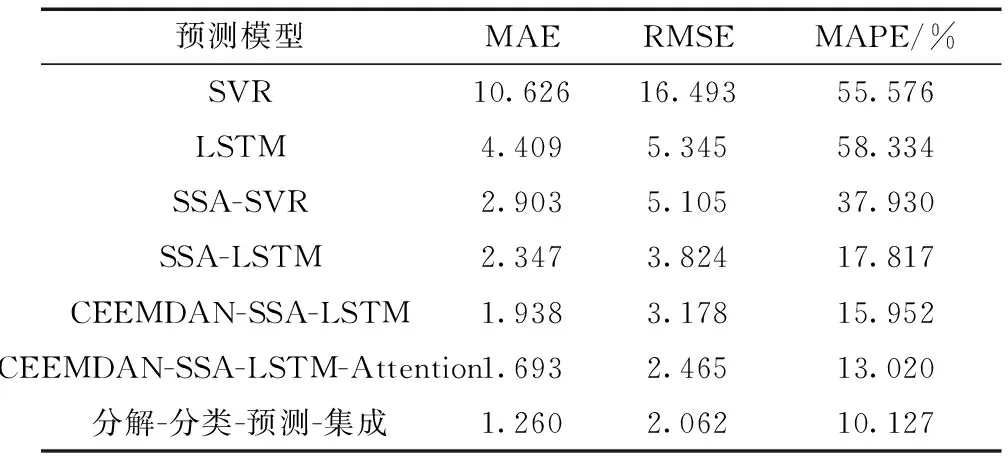
式(26)中:Q为服从正态分布的随机数;L为所有元素为 1的单位向量;R2为警告值,其范围是[0,1];ST为安全阈值,其取值范围是[0.5,1]。R2 由于加入者和发现者的身份不断地互换并一直寻找更好的食物来源。加入者的位置更新为 (27) 最后,根据麻雀寻优的规则和式(28)更新侦察员的位置为 (28) 步骤1初始化种群数量,并进行参数确定。 步骤2计算适应度值,并进行排序。 步骤3分别利用式(14)~式(16)来更新捕食者位置、加入者位置以及警戒者的位置。 步骤4根据计算出的适应度值来更新麻雀占有的新位置。 步骤5若满足条件,则停止迭代并输出结果,否则重复执行步骤2~步骤4。 SSA优化流程图如图2所示。 图2 SSA优化流程图Fig.2 SSA optimization flow chart Attention机制(Attention mechanism)的原理是在模型输出时会选择性地考虑输入中的对应相关的信息,计算每个特征的权重,对重要特征赋予较高的权重,对不重要的特征给予较低的权重。在解决循环网络的短期记忆问题时,能将有用的信息留下,并将不重要的信息进行忽略。 注意力模型的结构如图3所示。 图3 注意力机制模型结构图Fig.3 Structure of the attention mechanism model 设h=(h1,h2,…,hi,…,hn) 表示通过LSTM网络后得到的风电状态向量,hi是其中的一个状态向量,对应于hi的注意力αi,其计算公式为 ei=a(ct,hi) (29) (30) 式中:ei为得到的注意力值;ct为LSTM在t时刻的状态向量;α用来计算ct与hi之间的相关性的大小;αi由ei进行指数非线性变换得到。计算注意力加权特征向量ε的公式为 (31) 由于注意力机制使序列建模突破了距离的限制,因此注意力机制通常和循环神经网络联合使用。将注意力加权后的特征向量输入LSTM模型中进行训练,LSTM与AM的结构图如图4所示。 y为输出值;v为整合各部分权重后的新函数图4 LSTM-AM机制结构图Fig.4 Structure diagram of LSTM-AM mechanism 短期风电功率预测具体步骤如下。 步骤1使用CEEMDAN将原始风电功率序列分解为IMFs分量和一个残差量。 步骤2采用模糊熵算法对CEEMDAN分解出的子序列分量进行频率识别,重构成新的分量类型,并将其分为高频和中频分量。 步骤3针对高中频分量具有波动较大、振幅较大的特征,选择用注意力机制结合SSA-LSTM组合算法进行预测。 步骤4对于残差趋势项(RES)波动较小、信号较为平稳的特征,则采用SSA-SVR组合算法进行预测。 步骤5重构步骤3、步骤4中所得的序列预测分量,得到预测结果。 步骤6将不同模型预测所得的预测值通过误差评价指标来分析各个模型的相关性能。 短期风电功率预测流程图如图5所示。 图5 短期风电功率预测结构图Fig.5 Structure of short-term wind power forecast 以风电场2017年6—7月实际风电功率数据为例进行建模,其中包括风速、风向、大气密度等,且每两组数据之间的采样间隔为 15 min,算例中采集5 856个数据样本, 其中最高发电功率为49.017 MW,最低发电功率为3.234 MW,所得平均发电功率为14.62 MW。选用样本数据前90%作为训练集,后10%为测试集来进行训练、预测。 在采集风电功率相关的特征数据时,例如风速、风向、风电功率等特征,其数量级和数量单位都各不相同,有的数量级甚至相差极大,造成无法对各影响特征进行有效分析的问题。为了解决这一问题,将所有的历史数据先做归一化处理[22],即将所有数据映射到[-1,1],表达式为 (32) 式(32)中:xmin和xmax分别为输入数据的最小、最大值。 选用的误差评价指标为平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE) 和均方根误差(root mean square error,RMSE),各误差计算公式如下。 (33) (34) (35) 为了提高风电功率最终的预测精度,同时降低风能本身随机性和波动性对预测的影响。所以采用CEEMDAN分解算法对归一化后的原始数据进行预处理,其分解所得的各IMFs分量如图6所示。 图6 CEEMDAN分解分量Fig.6 CEEMDAN decomposition components 在图6中,将预处理后的数据分解为13个频率各异的IMF分量。IMFs分量按频率由高到低排列且各个分量之间保持较高的独立性。其中,高频信号分量波动性较大,其反映了原始功率序列较大的波动性,在预测时会产生较大的误差。低频信号分量较为平稳,接近一条平滑的曲线,其反映了原始序列平稳的变化趋势,在预测时能够较好地拟合效果。 在经过CEEMDAN分解后,不同的分量具有不同的频率特征。为了能更好地对模态分量的频率特征进行识别,CEEMDAN分解后使用模糊熵(fuzzy entropy,FE)复杂度算法将各模态分量进行类别划分。模糊熵算法是用来衡量时间序列动态状态的无序性,计算所得的FE越高,意味着时间序列的复杂度越高。因此,基于FE对模态分量进行分类,频率特征识别过程如下。 步骤1基于模糊熵算法计算模式k的复杂度FEk,k=1,2,…,M。 步骤2设置临界值λ0(2.3)和λ1(1.6)。 步骤3根据FE,对各模态分量imf进行类别划分。imf1,imf2,…,imfK被识别为短期扰动项(FE>λ0);imfK+1,imfK+2,…,imfL被识别为中期变化项(λ1 模糊熵算法参数设定采用嵌入维度m=2,r=0.141 4σsd,n=2。基于模糊熵值(FE)对模态分量进行类别划分,表1呈现了各模态分量的模糊熵值及分类结果。 表1 各分量模糊熵值及分类结果Table 1 Fuzzy entropy values and classification results of each component 根据不同序列分量的特点,并对不同分量的预测模型进行更合理的分析,分别选用合适的模型进行预测。对于较为平稳、波动性较小的序列,整体呈现出线性趋势,基本代表整个风电功率的长期走向趋势,采用对较平稳信号预测效果较好的SVR预测模型进行滚动预测并采用SSA对SVR相关参数进行参数寻优。由于高频类的信号波动性大,具有复杂的非线性关系。因此,选用经注意力机制进行权值分配后的LSTM 神经网络对中、高频分量类进行时序滚动预测,并用SSA对LSTM-Attention进行参数寻优。 根据高频序列中的相关特征进行建模预测分析。在SSA优化模型中,得到优化后的学习率最终稳定在0.006 8,最优迭代次数为58用K表示,且由优化后相关参数可知,第1隐含层和第2隐含层节点数最终稳定为100和43,分别用L1和L2表示。SSA优化效果随迭代次数的变化用lr表示。对高频序列模型进行SSA优化相关参数如图7和图8所示。 图7 SSA超参数随迭代次数的变化(高频序列模型)Fig.7 Variation of SSA hyperparameters with the number of iterations (high-frequency sequence model) 图8 SSA适应度变化曲线(高频序列模型)Fig.8 SSA adaptability change curve (high-frequency sequence model) 根据中频序列中的相关特征进行建模预测分析。在SSA优化模型中,得到优化后的学习率最终稳定在0.006 7,最优迭代次数为49,且有优化后相关参数可知第1隐含层和第2隐含层节点数最终稳定为49和90。对中频序列模型进行SSA优化相关参数如图9和图10所示。 图9 SSA超参数随迭代次数的变化(中频序列模型)Fig.9 Variation of SSA hyperparameters with the number of iterations(medium frequency sequence model) 图10 SSA适应度变化曲线(中频序列模型)Fig.10 SSA adaptability change curve (medium frequency sequence model) 对于高频分量和中频分量在分别进行SSA优化时,参数上的差异表现如图7~图10所示。对于一组数据在进行优化时,都选用了LSTM进行预测,但是由于数据频率波动上的差异,可将其按照一定的频率标准划分之后再进行优化,其优化参数也会大不相同,这证明了两组数据分别建立预测模型后再分开优化,预测精度也会随着优化参数的精确而进一步提高。而在对低频趋势项进行预测时,则选用泛化能力较为出色、且对异常值的鲁棒性较好的SVR进行功率预测。这种针对不同频率选用不同预测模型的方法,能更大限度地利用不同模型的优点,使得预测精度更佳。对SVR进行参数寻优,主要是对惩罚参数c、核参数g进行寻优[23],选用均方误差(mean square error,MSE)作为适应度函数的评价标准,其计算公式为 (36) 在迭代次数100、种群数量为20的情况下,经过不断优化可得最后的最优惩罚参数c为12.245 8,最优的核参数g为0.768 11,MSE为此时模型的误差评价指标,为6.076 9,结果如图11所示。 图11 SSA优化SVR相关参数Fig.11 SSA optimization of SVR-related parameters 由于原始功率波动性较大,且数据特征较为复杂。使用单一的预测模型进行功率预测时,会出现明显的不足,而在进行预测前,采用CEEMDAN分解能有效降低原始数据的复杂程度,为进一步分频预测打下基础。且使用不同的单一模型对同一数据进行预测时也会出现明显的差异,比如使用单一的LSTM和SVR对功率进行预测,则会发现LSTM在数据波动较大、数据量增多的情况下预测效果更佳,相反SVR在数据较为平滑、波动较小时预测效果更好,且其对于数据较多的情况往往难以展现其优点。所以采用不同模型进行分频处理,得到的整体预测效果更好。 为了更好地评估所提出模型的性能,选用SVR、LSTM、SSA-SVR、SSA-LSTM、CEEMDAN-SSA-LSTM、CEEMDAN-SSA-LSTM-Attention共6种预测模型与所提的“分解-分类-预测-集成”模型进行对比,结果如图12所示。 图12 不同模型预测值对比Fig.12 Comparison of predicted values of different models 分别计算SVR、LSTM、SSA-SVR、SSA-LSTM、CEEMDAN-SSA-LSTM、CEEMDAN-SSA-LSTM-Attention和“分解-分类-预测-集成”模型的评价指标MAE、MAPE、RSME的值,如表2所示。 表2 不同模型的误差评价指标Table 2 Error evaluation index of different models 由图12可得出,在功率波动较平稳的点SVR的预测效果明显优于LSTM,但是在波动较大的点,SVR显然达不到较好地预测效果,而LSTM则能较好地进行波动较大处的预测。充分验证了SVR对于较为平滑且稳定的点有较好的预测效果,而LSTM则可以对波动较大的数据点进行更好的预测处理。首先,经过对比可以发现,原始数据经过CEEMDAN分解后再进行预测,所得到的误差评价指标均要比直接进行预测时效果更好,从表2中不难发现CEEMDAN-SSA-LSTM预测模型相较于SSA-LSTM模型,MAE、RMSE和MAPE分别下降了0.409、0.664、0.048。此外,相较于传统的用经验来进行LSTM的超参数选择方法,在经过SSA优化后的LSTM能更好地体现预测性能,MAE、RMSE和MAPE分别下降了2.062、1.521、0.405。 所提出的“分解-分类-预测-集成”预测模型起到了较为明显的预测效果,针对低频的趋势项采用鲁棒性更强的SVR进行预测;对于波动和振幅较大的高、中频项则采用LSTM行预测,并采用SSA对这两个模型参数进行寻优。该模型相较于CEEMDAN-SSA-LSTM-Attention的MAE、RMSE和MAPE分别下降了0.433、0.403和0.03。并且使得预测效果更好,对整个预测都采用SSA-LSTM比采用SSA-SVR的MAE、RMSE和MAPE分别下降了0.556、1.281和0.201。同时,对于模糊熵重构的序列中的中、高频分量都采用了LSTM预测,但是在用SSA进行优化时,由于波动程度及幅值大小的整体差异,在进行参数优化时,所得到的优化参数也会各不相同,如前者第1隐含层和第2隐含层节点数最终稳定为49和90,而后者第1、2隐含层节点数最终为100和43。经过这种分频的优化使得模型的整体预测精度进一步提高。 对于所提出的分解-分类-预测的预测框架,经过实验分析得到如下结论。 (1)研究CEEMDAN分解方法、模糊熵分类法、SSA优化算法以及LSTM和SVR预测算法,提出了基于频率的不同对序列进行重构的模糊熵分类法和对不同频率序列采用不同模型进行预测的组合模型,目的是为了提高短期风电功率的预测精度。 (2)经过 CEEMDAN 分解对原始数据的预处理,把原本复杂的功率数据分解为多个简单序列,减小了原始数据的不平稳性。同时,考虑到子序列波动程度的不相同,采用了模糊熵将序列分量按FE值进行重构,分为高频和中频分量。 (3)使用SSA分别对SVR和LSTM预测模型进行超参数优化,使用SSA-LSTM对高中频分量进行预测;使用SSA-SVR对低频趋势项进行预测。由于高、中频序列分量的整体波动程度及幅值大小各不相同,因此在采用SSA对LSTM进行超参数优化时,会发现其优化参数也各不相同。在对不同频分量分类后,进一步提高了模型的整体预测精度。 (4)其他6种模型与所提出的模型进行对比,可以明显地发现所提模型在很大程度上克服了单一预测模型易陷入局部最优的缺点,且其有着更好的动态预测性能,因此,有着更为精确的预测效果。进一步证明了所提出模型的合理性及精确性,对风电功率的短期预测有着更好的实际应用意义。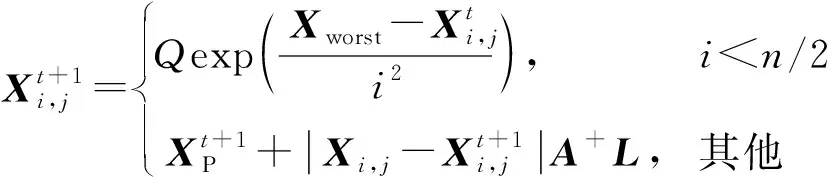


2.4 注意力机制
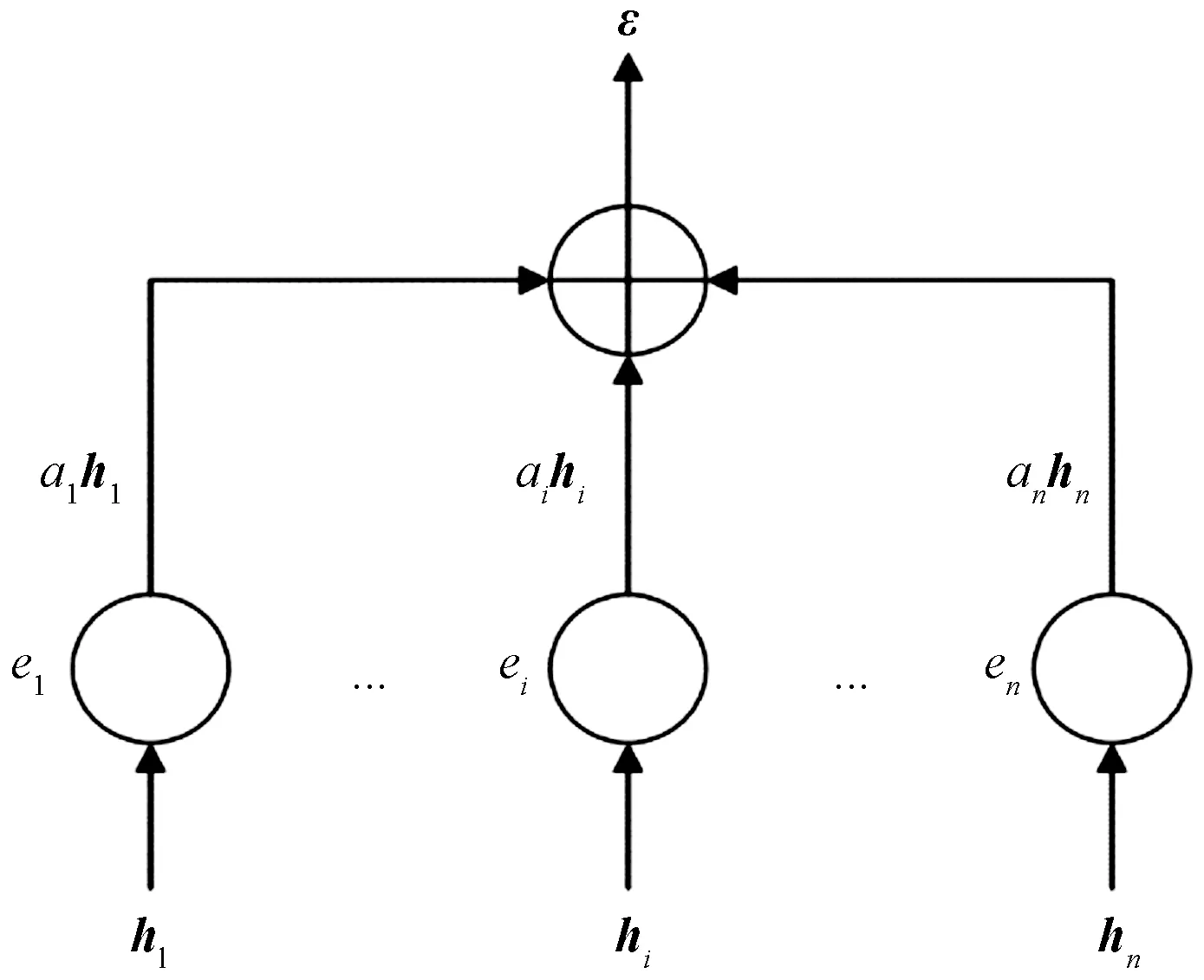
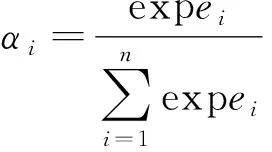

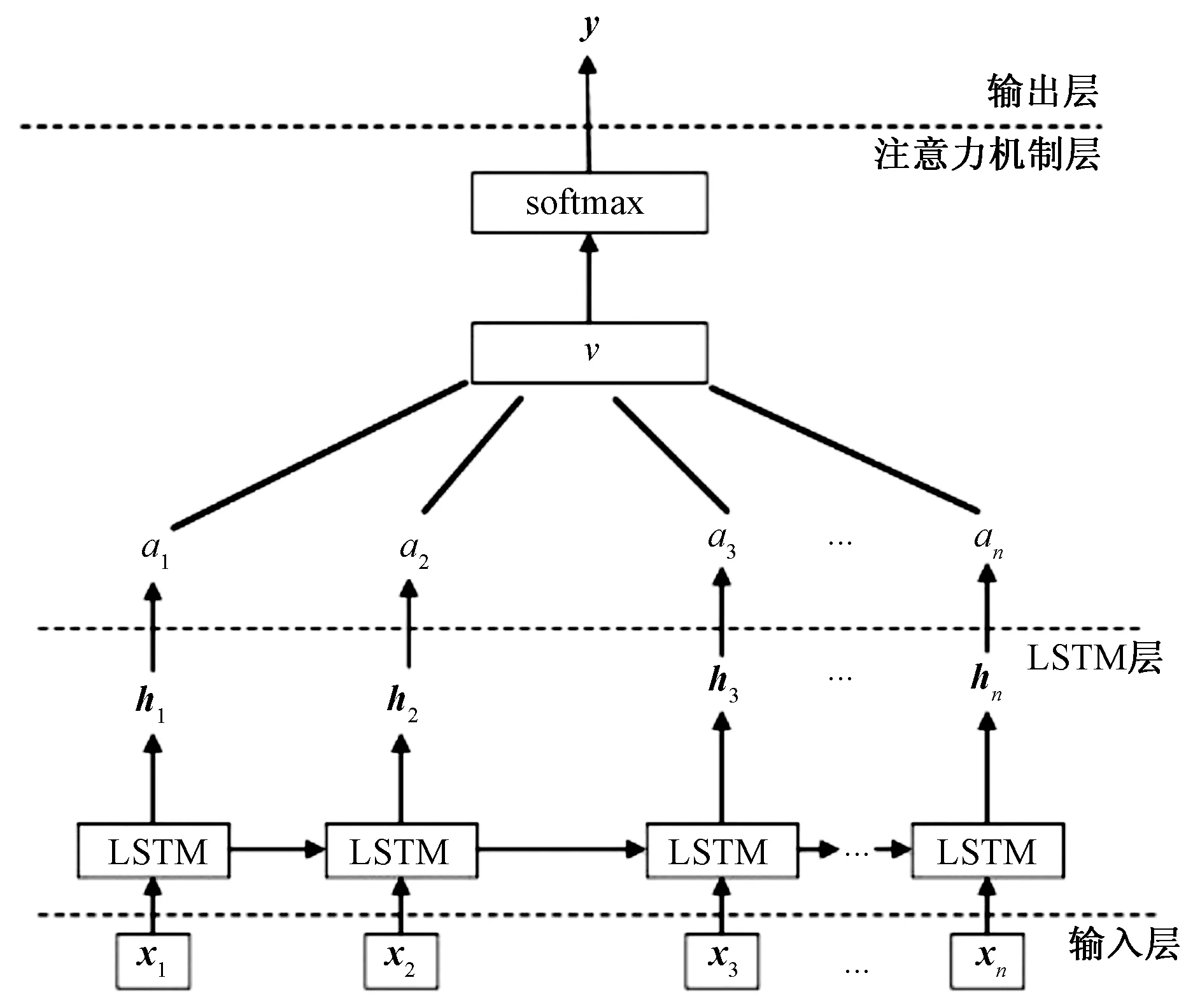
3 预测流程

4 短期风电功率预测与结果分析
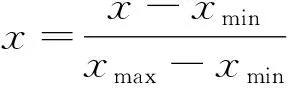

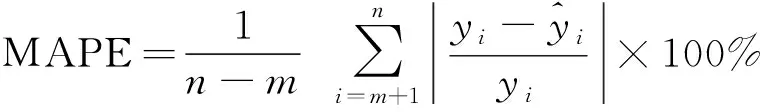
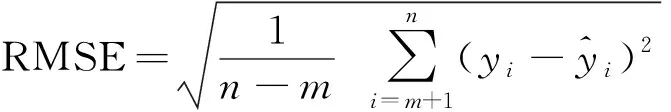

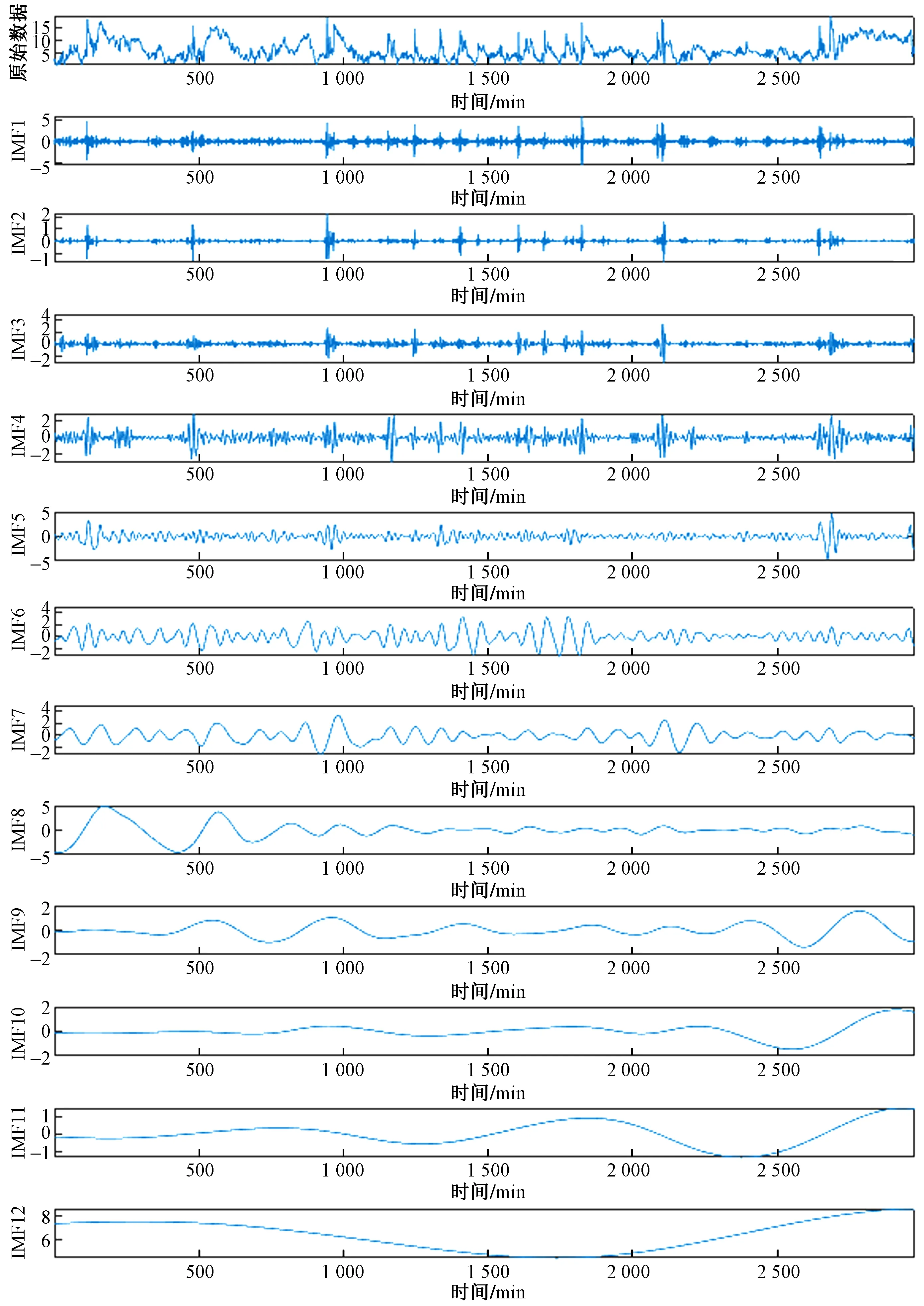
4.1 基于CEEMDAN的风电功率序列分解
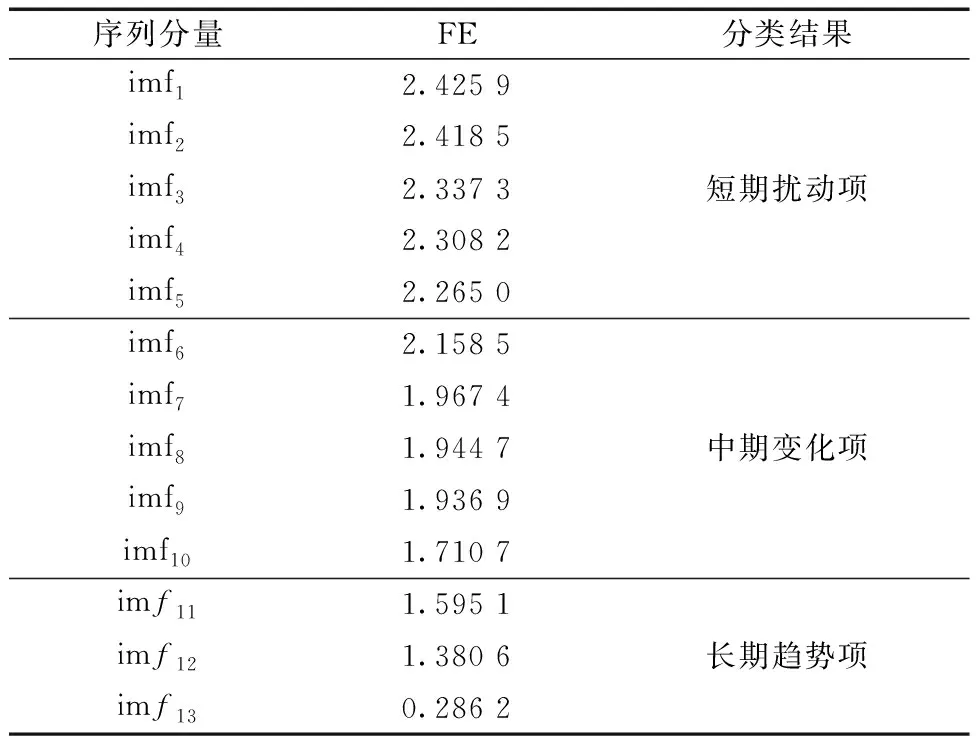
4.2 模糊熵模态分量特征识别
4.3 预测结果分析

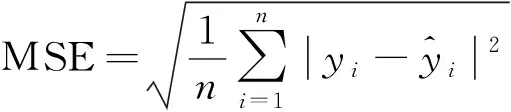

5 结论

