基于双重介质嵌入式离散裂缝模型的致密油藏产能影响因素

肖尊荣, 赵玉龙*, 张烈辉, 葛枫, 杨志冬, 刘香禺, 张东旭, 田野

(1.油气藏地质及开发工程国家重点实验室(西南石油大学), 成都 610500; 2. 中国石油西南油气田公司致密油气勘探开发项目部, 成都 610000; 3.中国石油新疆油田分公司百口泉采油厂, 克拉玛依 834000)

随着常规油气资源的不断枯竭,致密油藏逐渐成为勘探开发的热点[1-5]。中国致密油地质资源量为125亿t,是推动油气增储上产的重要力量[6]。致密油储层普遍存在强非均质性,其孔隙结构复杂,压力异常偏高,具有强应力敏感,表现出明显的超低孔超低渗特征,油气资源高效动用面临巨大挑战[7]。生产实践表明,长水平井段体积压裂是实现致密油资源经济高效开发的关键技术[8-11]。因此,建立考虑复杂缝网的渗流数学模型,进而开展致密油藏压后产能预测、生产动态规律预测等,是实现致密油藏经济高效开发不可或缺的技术手段。

针对上述关键问题,国内外学者开展了大量研究工作,相继提出了双重孔隙介质模型、离散裂缝模型和嵌入式离散裂缝模型[12-14]。双重孔隙介质模型假设裂缝均匀分布在储层中,基质为主要的储集空间且具有一定的渗流能力,裂缝为主要的渗流通道[15]。孙若凡等[16]基于该模型建立了致密油藏压裂水平井数值模型,进一步研究了应力敏感系数、裂缝半长、裂缝间距等因素对产能的影响。需要注意的是,双重介质模型不能较好地描述具有特殊导流能力的裂缝,在等效渗透率确定方面也存在困难。为了准确描述地层中具有特殊导流能力的裂缝,Noorishad等[17]、Baca等[18]提出了离散裂缝模型(discrete fracture model,DFM)。在离散裂缝模型中,基质被划分为矩形单元,裂缝被划分为线段单元,每条裂缝都由单元或控制体显性表征,裂缝参数通过裂缝诊断检测、裂缝扩展地质力学模拟等方法获得,模型具备较高计算精度[19]。不足的是,由于网格剖分时会在裂缝周围产生大量非结构化网格,导致DFM运算速度不佳。随后,Mi等[20]和Li等[21]提出了离散裂缝网络模型(discrete fracture network,DFN),与DFM不同的是DFN仅在裂缝相交处对裂缝进行离散,有效减少了网格的数量,提高了处理裂缝网络的能力;Altman等[22]基于DFN模型建立了科威特西部的Najmah-Sargelu致密油藏数值模型,研究了天然裂缝网络对产能的影响,并对该致密油藏制定后续开发生产方案提供了指导。当地层中裂缝分布复杂时,DFN网格剖分过程较为烦琐,并且当裂缝距离较近时,网格剖分质量较差,计算精度不高[21]。为此,Lee等[23]、Li等[24]将连续介质模型与离散裂缝模型相结合,提出嵌入式离散裂缝模型(embedded discrete fracture model,EDFM),采用不同方法模拟不同长度的裂缝:短裂缝被等效处理到基质网格渗透率中,结合边界元和格林函数模拟中等长度裂缝;对于长裂缝,借用井指数的概念,定义了一个传导率参数来描述基质网格与该网格中的裂缝段之间的流体交换。将短裂缝等效处理到基质网格渗透率中会导致模型的准确性受到影响,可能导致模拟油井产能存在偏差,且存在难以三维模型中准确表征裂缝形态的问题。饶翔等[25]发明了一种适用于三维任意形状裂缝面表征的方法。周瑞[26]使用商业软件Eclipse验证了该方法的正确性。牛骏等[27]通过建立耦合EDFM和扩展有限元建立了一种基于裂缝性页岩模拟生产动态过程中裂缝几何形态变化的方法。Monifar等[28]将EDFM(精细刻画水力裂缝)与双重介质模型(表征天然裂缝)相结合提出了双重介质嵌入式离散裂缝模型(dual porosity embeded discrete fracture model,DPEDFM)以解决EDFM中采用等效渗透率模拟中小裂缝引起基质网格渗透率缺少的问题。

为解决致密油藏多级压裂水平井开采过程中多相、多尺度传质导致的产能评价困难的问题,在DPEDFM的基础上,现采用全隐式差分求解,运用连接对理论组装矩阵,编制相应数值模拟器。最后,基于所建立的模型研究天然裂缝、水平段长度、人工裂缝间距等因素对致密油藏产能的影响规律。

1 数学模型建立及求解

1.1 模型假设

在建立的双重介质嵌入式离散裂缝模型中,基质和天然微裂缝在整个油藏区域是相互重叠的连续体,天然微裂缝以单一尺度、统一分布和全部联通的形式嵌于基质块中,两个连续体在空间上重叠,但拥有相互独立的属性体,如图1所示。模型其余假设如下。

m1、m2、m3、m4为4个正方形网格;f1、f2、f3、f4为4个天然裂缝网格;edf1、edf2为2个嵌入式离散裂缝网格;w1为井网格图1 双重介质嵌入式离散裂缝模型Fig.1 Dual porosity embeded discrete fracture model

(1)油井生产过程为等温、油水两相流动。

(2)将致密油储层简化为双孔双渗系统,基质网格和天然裂缝网格分别具有一套各自的储层性质。

(3)基于嵌入式离散裂缝模型简化储层中水力裂缝。

如图2所示为双重介质嵌入式离散裂缝模型流动单元划分示意图,该二维模型中包括一口水平井、一条水平裂缝。模型的基质部分被划分为4个正方形网格(m1、m2、m3、m4);同时,在空间上存在与基质部分相重合的4个天然裂缝网格(f1、f2、f3、f4);人工裂缝穿过m1、m2,被划分为2个嵌入式离散裂缝网格(edf1、edf2),并且与天然裂缝f1和f2相交。

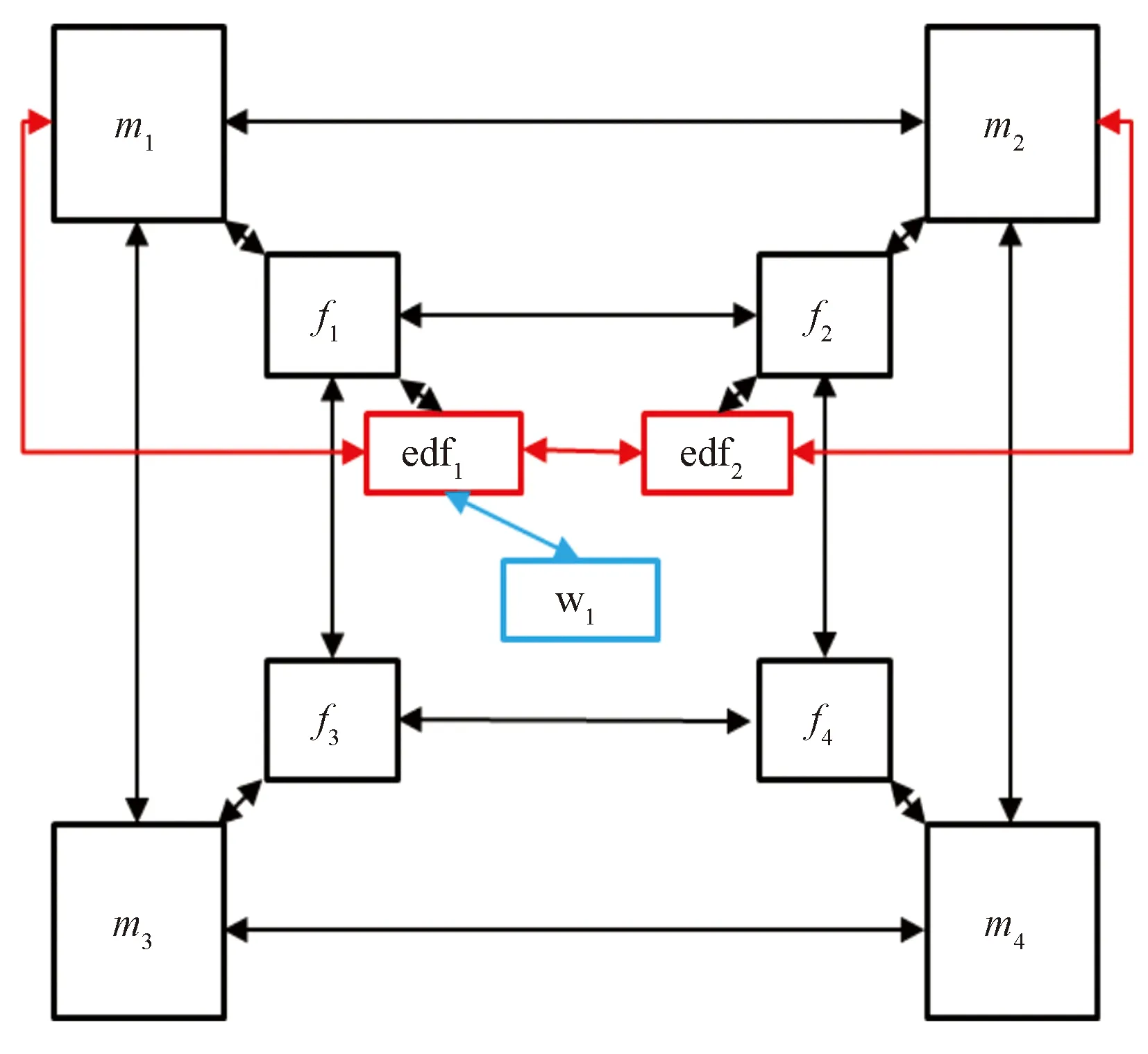
图2 连通性示例图Fig.2 Example diagram of connectivity

1.2 数学模型建立

考虑基质与天然裂缝中存在的流体微可压缩,岩石存在一定可压缩性,存在毛细管力;假设水力裂缝中存在的流体微可压缩、水力裂缝网格不可压缩且忽略网格中毛细管力。

1.2.1 油水两相流基本渗流微分方程

由两相物质平衡可得出方程式如下。

(1)基质、天然裂缝系统。

(1)

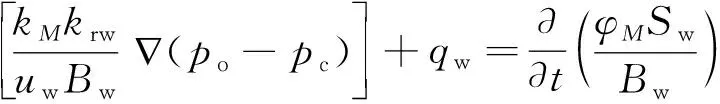
(2)

式中:M=m、f,分别表示基质和裂缝;kM为M网格的渗透率,D;kro、krw分别为油相、水相相对渗透率;po、pc分别为地层中油相压力、毛管压力,kPa;uo、uw分别为油相、水相黏度,Pa·s;Bo、Bw分别为油相、水相体积系数;qo、qw分别为油相、水相从其他类型介质中进入该介质时的流量,m3/d。

(2)沿人工裂缝局部坐标建立人工裂缝系统渗流方程。

(3)

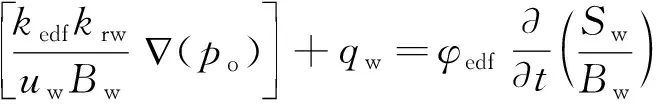
(4)

式中:kedf为人工裂缝网格的渗透率,D。

1.2.2 天然微裂缝渗透率应力敏感效应

分析应力敏感对产能的影响时,主要采用应用较为广泛的指数关系模型,即

k=k0e-α(p0-p)

(5)

式(5)中:k0为初始渗透率;p0为初始压力;e为自然对数;α为应力敏感系数,kPa-1。

1.2.3 传导率计算

在双重介质嵌入式离散裂缝模型中,会形成3种不同介质间窜流连接对,分别为基质-天然微裂缝、基质-人工裂缝、天然微裂缝-人工裂缝。不同介质间传导率系数计算式为

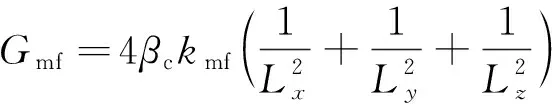
(6)

式(6)中:kmf为基质与裂缝间窜流时渗透率,D;Lx、Ly、Lz分别为基质网格在x、y、z方向上的长度,m;βc为传导率转换因子,取值为86.4×10-6。

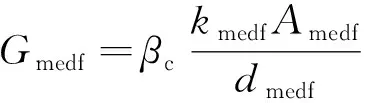
(7)

(8)

式中:Amedf、Afedf分别为基质网格、天然裂缝网格与嵌入式离散裂缝网格相交的面积,m2;dmedf、dfedf为平均正交距离,分别表示基质网格、天然裂缝网格与裂缝网格间的等效距离,m。

在人工裂缝与井眼相交时,采用垂直井网格和井底压力间的Peaceman模型,表达式为

(9)

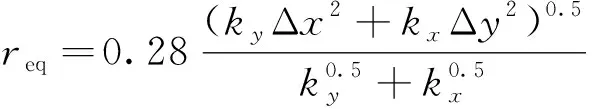
(10)

式中:Δx、Δy、Δz为井所在基质网格x、y、z方向尺寸,m;req为供给半径,m;rw为油井半径,m。

Peaceman模型是在未考虑裂缝的条件下提出的,Moinfar[32]结合EDFM模型对Peaceman模型进行了改进,即

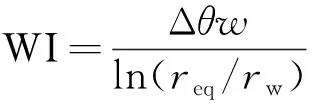
(11)

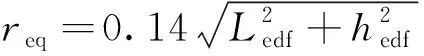
(12)

式中:w为人工裂缝裂缝开度,m;Ledf、hedf分别为人工裂缝段的长度、高度,m;Δθ为径向井包含在裂缝内的圆心角角度,rad。一般情况下,Δθ=2π。

1.3 数学模型求解

采用有限差分对双重介质嵌入式离散裂缝模型求解,得到其有限差分格式如下。

根据基质与人工裂缝的关系,分为无人工裂缝和有人工裂缝两种情况。无人工裂缝则有限差分格式中窜流相MEDFi,j=0,FEDFif,jf=0。

1.3.1 基质网格

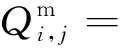
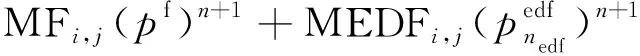
(13)

式(13)中:

式中:Vb为基质网格、天然裂缝网格或裂缝段体积;cl为液体压缩系数,MPa-1;Bi为原始地层压力下体积系数;下标i、j、if、jf、iedf、jedf分别为基质网格、天然裂缝网格、人工裂缝网格的i、j方向;上标n为时间步长;下标nedf为第n个与井眼连接的人工裂缝网格;MFi,j、MEDFi,j、FEDFi,j分别为基质与天然裂缝、基质与人工裂缝间窜流相。

1.3.2 天然裂缝网格

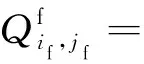
(14)

式(14)中:

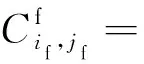
1.3.3 人工裂缝网格

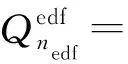
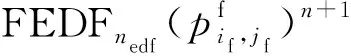
(15)

式(15)中:

如果存在裂缝向井眼中的流动,则有

(16)

式(16)中:EDFWnedf为人工裂缝向井眼的流动相。

2 模拟结果及讨论

2.1 模型验证

为验证本文模型的正确性,开展了双孔常规油藏采油过程的模拟。假设在所建立模型中,所有与基质网格空间上重合处均存在天然微裂缝,使用双重介质模型进行模拟;仅在水平井附近存在水力压裂缝,采用嵌入式离散裂缝模型进行模拟。并将模拟结果同商业软件Saphir计算结果进行了对比,随后采用某致密油藏实际水平井进行实例验证。采用商业软件Saphir验证模型时所建立模型大小为1 200 m×1 200 m×10 m,网格大小为40 m×40 m,人工裂缝半长为360 m,裂缝开度为0.005 m。流体参数见表1、图3。孔隙度、地层水体积系数、地层水黏度的计算公式如下。

表1 验证模型参数Table 1 Parameters of test model

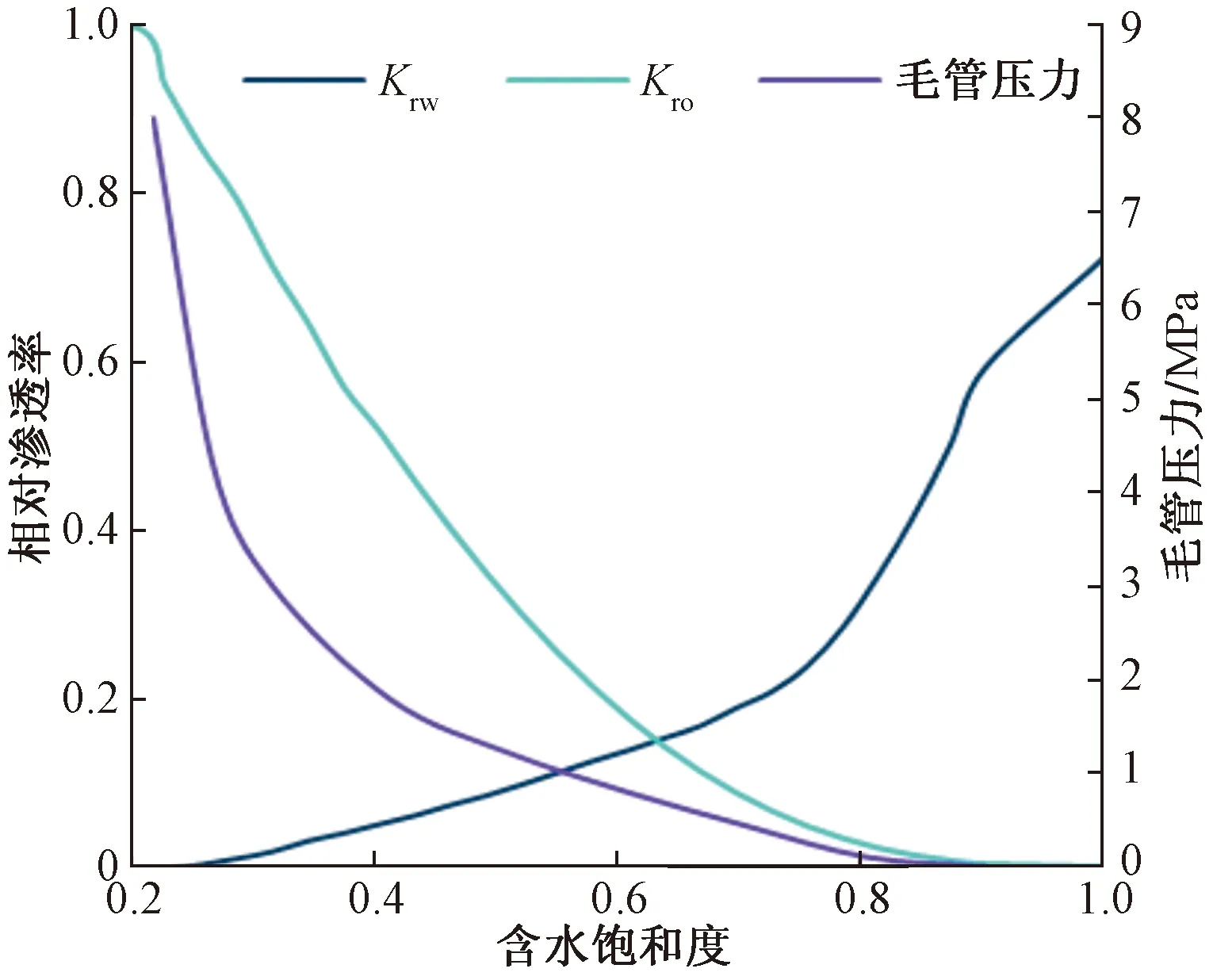
图3 油水相渗曲线和毛管压力图Fig.3 Relative permeability curve and capillary force chart

φ=φ0[1+Cf(p-p0)]

(17)

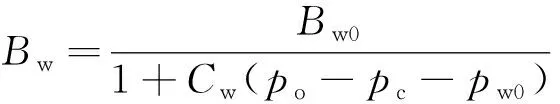
(18)

ρw=ρw0[1+Cw(po-pc-pw0)]

(19)

式中:Cf、Cw分别为岩石、水的压缩系数,MPa-1;φ、φ0分别为孔隙度、原始地层压力下孔隙度;Bw、Bw0分别为水的体积系数、原始地层压力下水的体积系数;p0、pw0、p分别为初始地层压力、初始水相压力、地层压力,大小为p0-pc,MPa-1;ρw、ρw0分别为地层水密度、原始地层压力下地层水密度,kg/m3。

从图4可以看出,Saphir模拟结果与本文模型的模拟结果具有较好的一致性;删除生产前50 d日产油量变化较大区间数据后,使用剩余数据进行方差分析,结果显示本文模型相对于Saphir日产油量平均误差为0.05。

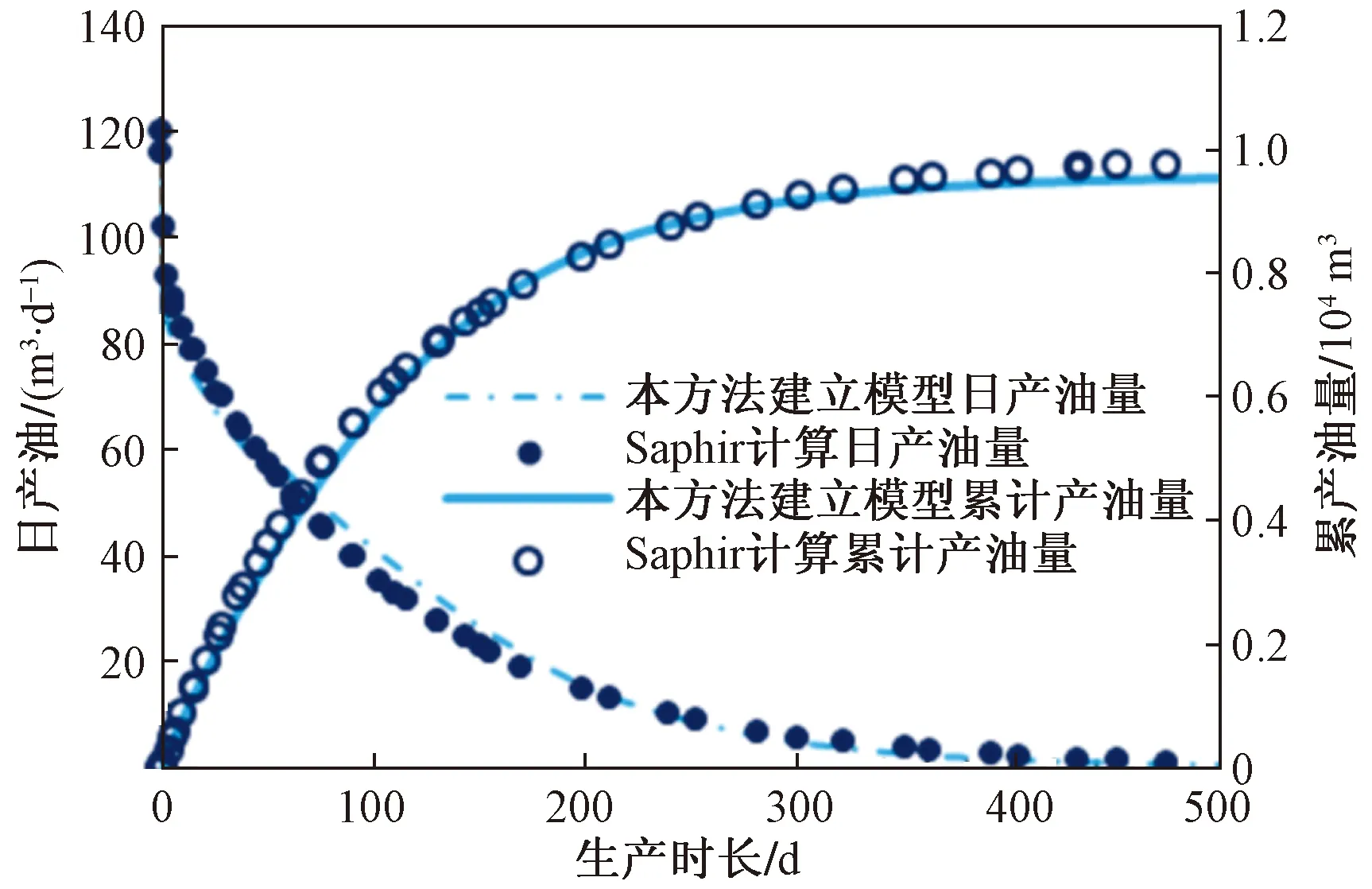
图4 产能对比图Fig.4 Production capacity comparison map

分别使用所编制模拟器与商业软件Petrel对新疆风城油田某多级压裂水平井(简称A井)开展生产历史拟合及产能动态预测;A井钻遇水平段长为1 378 m,所在主力层为三叠系百口泉组T1b2,通过测井解释以及室内岩心实验测得油层孔隙度为2.6%～13.8%,平均8.54%;渗透率0.01～3.51 mD,平均0.158 mD;含油饱和度46.4%～60.6%,平均53.8%。

使用商业软件petrel中的非常规裂缝模型(unconventional fracture model,UFM)对A井开展水力压裂缝网扩展模拟,水力压裂缝网如图5所示,并将压裂缝网导入所编写程序中。图5中矩形方框为SRV区,在此区域中附加前文所述天然裂缝模型以等效SRV区。获取流体属性、相渗等相关参数,如表2所示,所建立模型大小为1 800 m×600 m×20 m,网格尺寸为20 m×20 m×20 m。

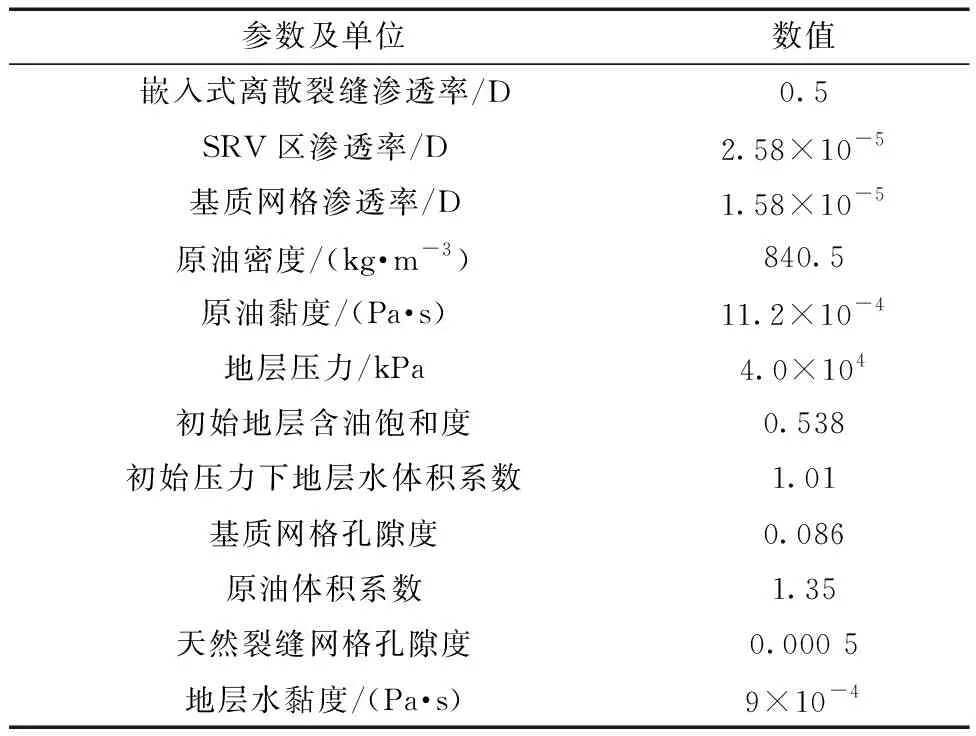
表2 实际矿场参数Table 2 Actual field data

图5 水力压裂缝网图Fig.5 Hydraulic fracture network diagram

生产历史拟合结果如图6所示,使用本模型对该油井进行生产历史拟合时,误差约为15%。在可接受范围内,结果具有较好的准确性;进而使用Petrel以及本文模型针对该井进行产能预测,预测结果如图7所示,结果表明本文模型预测结果与Petrel预测结果具有一致性;验证了所提出双重介质嵌入式离散裂缝模型(简称为DPEDFM模型)的准确性和适用性。

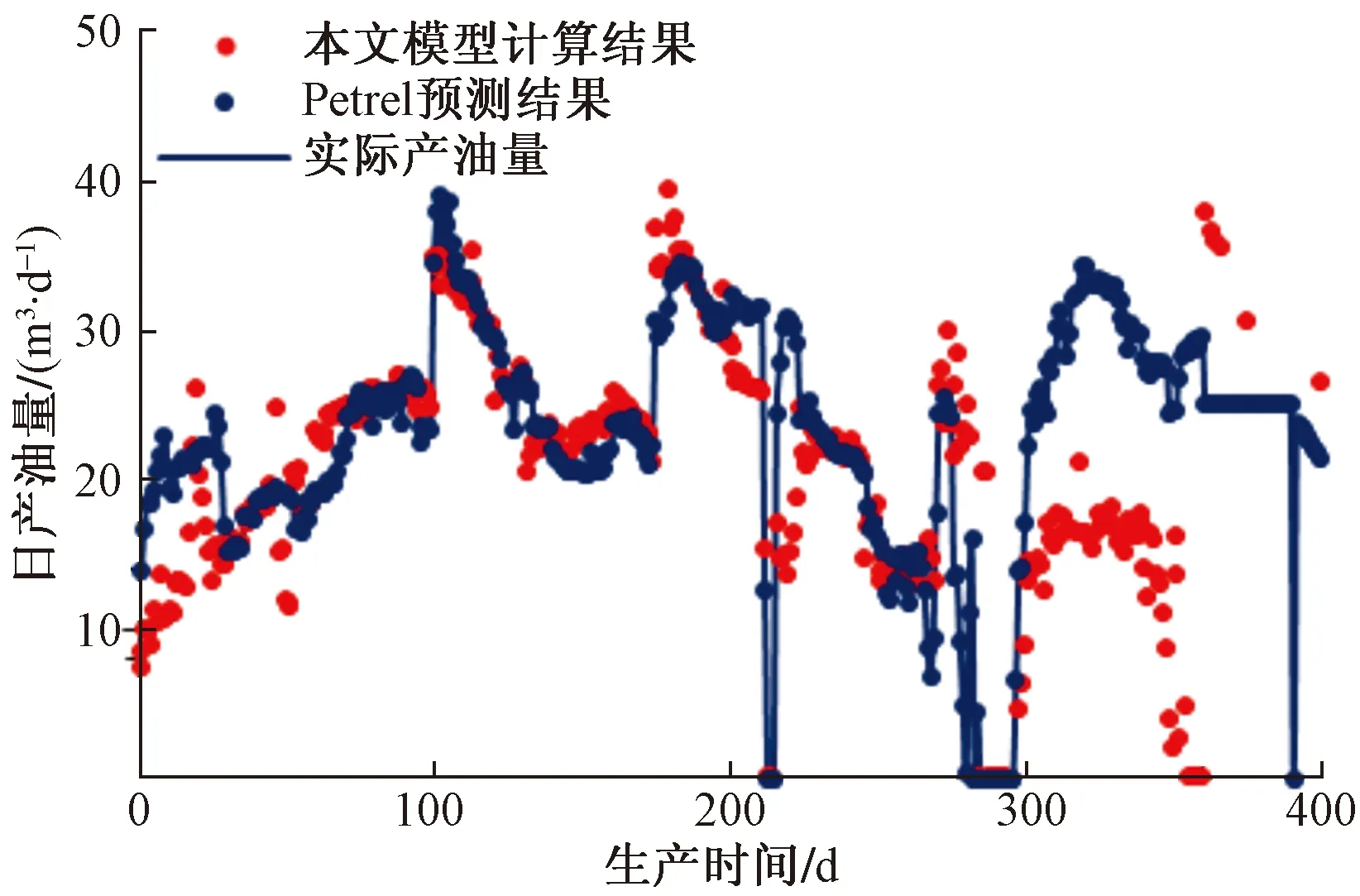
图6 日产油拟合对比图Fig.6 Daily oil fitting comparison diagram

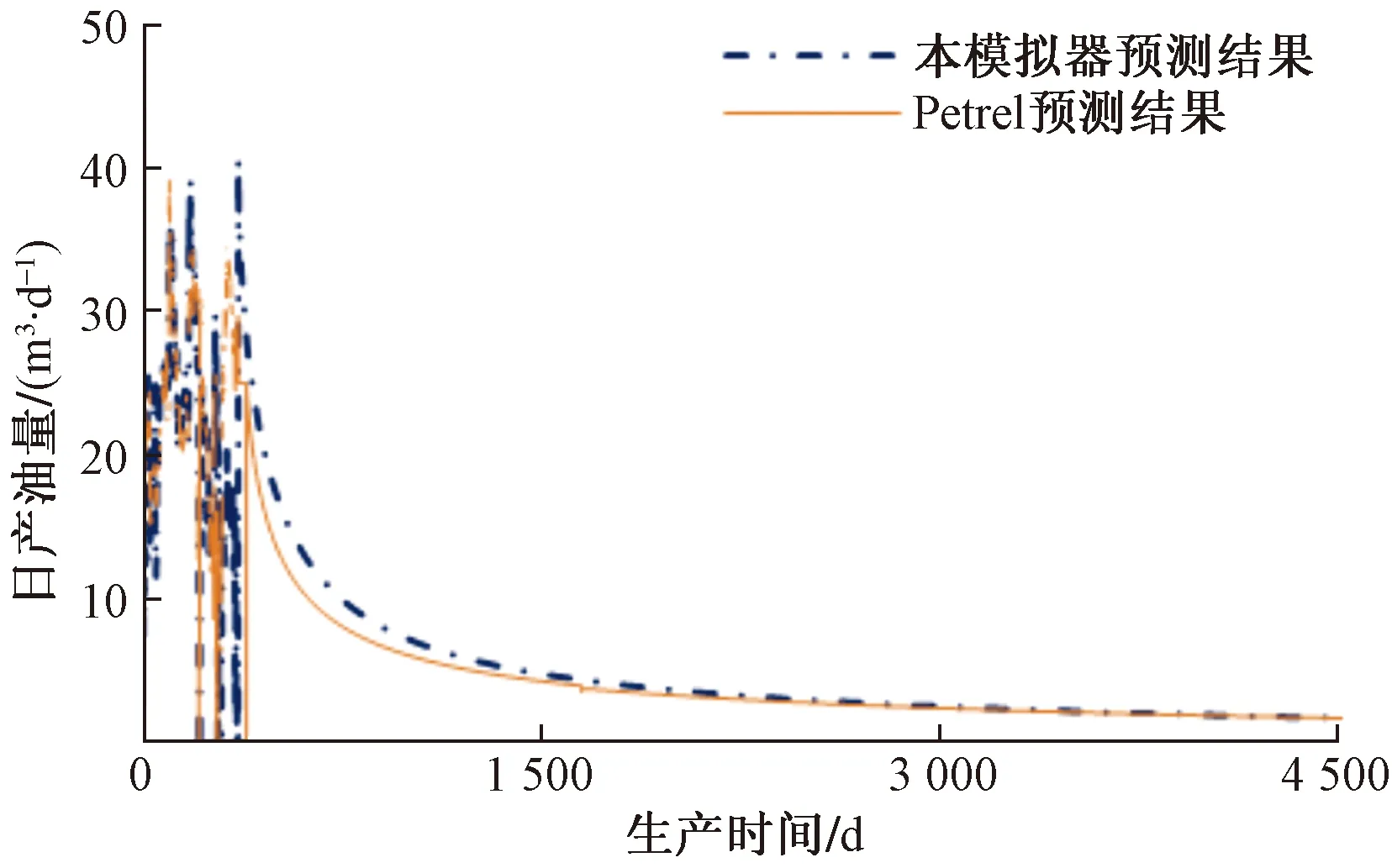
图7 日产油预测对比图Fig.7 Comparison of daily oil production forecasts

2.2 天然微裂缝对产能的影响

考虑致密油藏超低渗特征以及开发实际,将模型大小调整为1 800 m×600 m×10 m,裂缝长度为120 m,井底压力设置为15 MPa。为缩小网格尺寸对模拟结果的影响,将网格大小更改为20 m×20 m×10 m,天然裂缝均匀分布在整个模型当中,其渗透率设置为1.2×10-4D,基质网格渗透率均设置为0.8×10-4D,其余参数均采用表1中数据。

传统EDFM模型在处理天然微裂缝时,通常将其等效渗透率赋值到基质网格中且忽视天然微裂缝孔隙度,造成基质网格渗透率以及天然裂缝孔隙度缺失(简称为天然微裂缝属性体)。虽然上述属性数值较小,但其对原油渗流过程的影响不应该被忽视。为研究天然微裂缝属性体对产能的影响,设置水平段长度为1 200 m,分别设置裂缝条数为5、9、13、17,采用传统EDFM模型与本文模型进行模拟对比。

从图8可以看出,随着开井生产时间的增加,DPEDFM模型与EDFM模型计算得到的累计产油量差异逐渐增大,本文模型得到的累计产油量始终高于传统EDFM模型,这说明天然微裂缝属性体对累计产油量的影响不容忽视;随着开井生产时间增加,具有相同段数裂缝不同模型之间的日产油量差距逐渐减小,且裂缝条数越多,日产油量间差距缩小越快,这是因为裂缝段数增加,储层能量枯竭越快。模拟结果表明,传统EDFM模型计算得到的日产油量和累计产油量均低于本文模型,忽视天然微裂缝属性体可能会造成对油藏产能的错误估计。

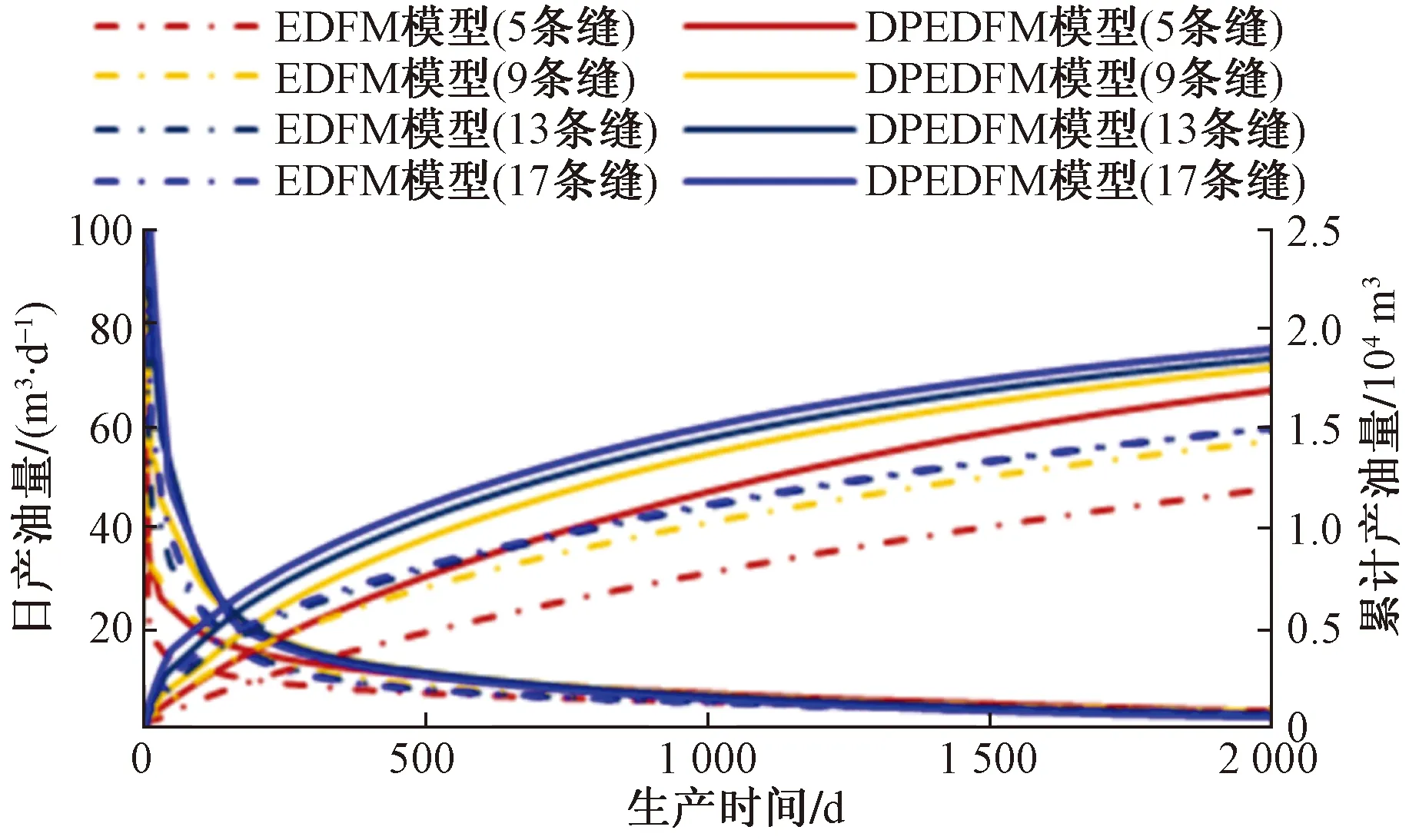
图8 不同模型产能曲线图Fig.8 Production capacity chart of different model

裂缝条数为13条时,两模型产水曲线如图9所示。可以看出,当生产时间达到80 d时,两模型累计产水量相等;EDFM模型产水速度下降更慢,这是因为在EDFM模型中,水力裂缝网格所在基质网格仅与水力裂缝网格间发生窜流,基质网格中的水直接流入水力裂缝中,地层水补充更及时;由于DPEDFM模型中水力裂缝网格同时与基质网格、天然裂缝网格相连接,模型初始产水速度更快,天然裂缝网格孔隙度非常小,因此产水速度下降更快。

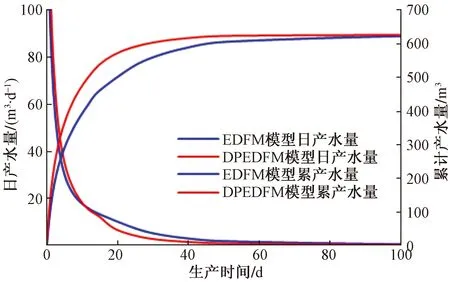
图9 DPEDFM模型与EDFM模型产水图Fig.9 DPEDFM and EDFM water production map

分析图10可知,DPEDFM模型在生产50 d时,裂缝处压力波已传至相邻裂缝,而EDFM模型在生产100 d时压力波才传至相邻裂缝。在生产相同时间时,DPEDFM模型中地层压力低于EDFM模型。综上所述,DPEDFM模型由于考虑了地层中天然微裂缝的影响,压力下降更快。

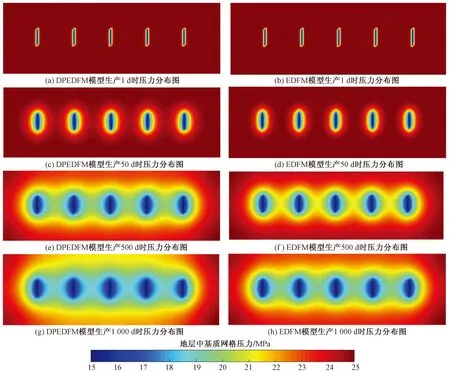
图10 DPEDFM模型与EDFM模型生产时地层压力对比图Fig.10 Reservoir pressure of DPEDFM and EDFM during production

2.3 水平段对产能的影响

2.3.1 水平井长度对产能的影响

水平井长度与经济成本有直接联系,增加水平井长度会增加经济成本,但同时也会提高产油量。为确定水平井长度与产能之间的关系,分别以2.1节中的矿场实际模型与2.2节所建立DPEDFM模型为基础开展了5组模拟实验,设置水力压裂缝长为120 m,裂缝间距为80 m,水平井长度为640～1 280 m;设置长为740 m～1 380 m、宽为220 m且中心与模型中心相重合的矩形为图5中矿场实际模型中SRV区。

从图11可以看出,随着水平井长度增长,日产油量、累计产油量增加且水平井长度越长,日产油量下降速度越快;如图12、图13所示,累产油量、采收率与水平井长度成近似线性关系且两模型的趋势线公式不一致。上述现象是因为增长水平井长度增大了水平井控制面积,生产前期,主要生产水平井控制面积内的流体,生产中后期,产能依靠控制面积外的储层维持;储层孔隙度、渗透率等储层参数改变,导致增长相同水平井长时,累计产油量、采收率增加的幅度不同。

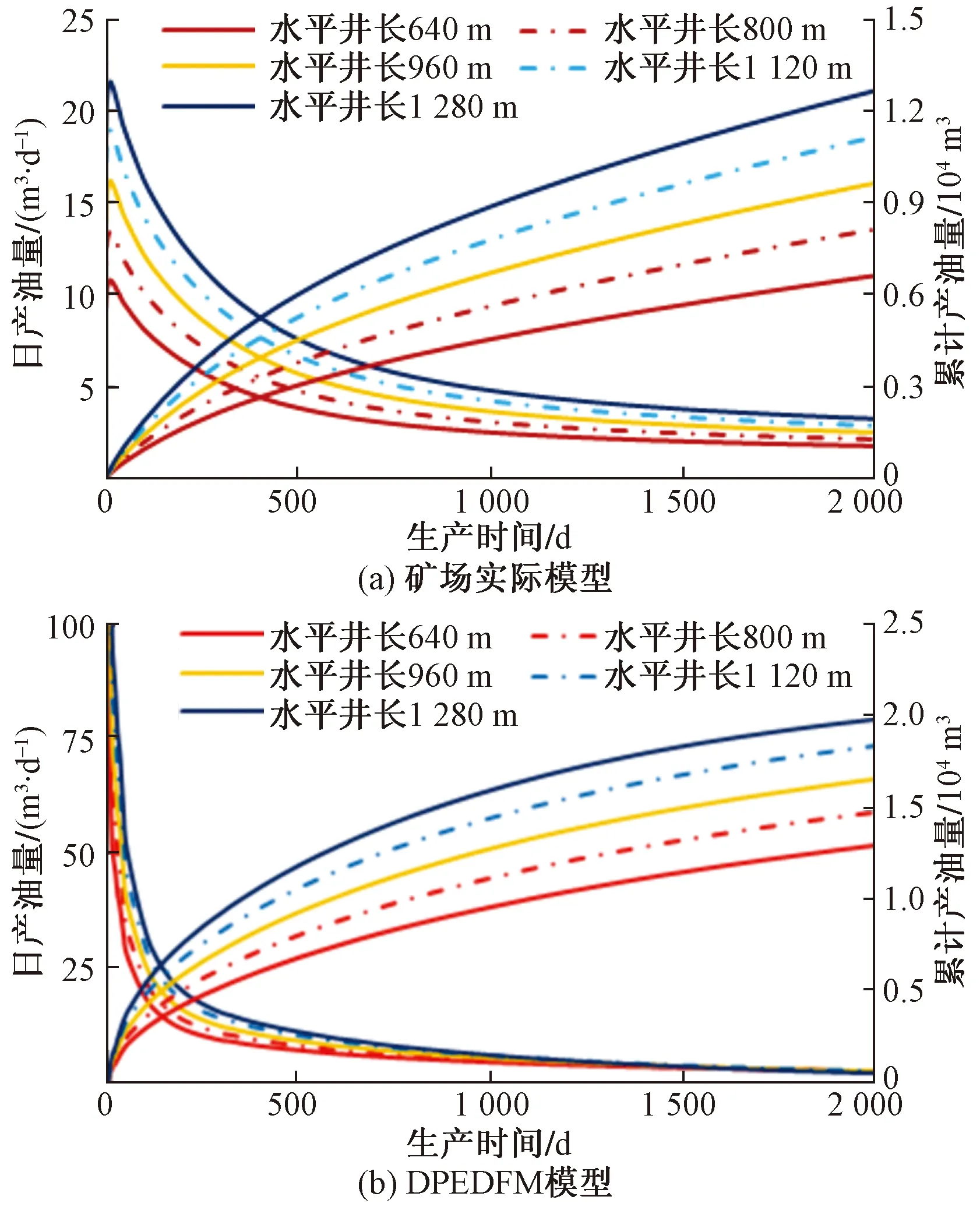
图11 不同水平段长时产能图Fig.11 Product capacity diagram for different length of well

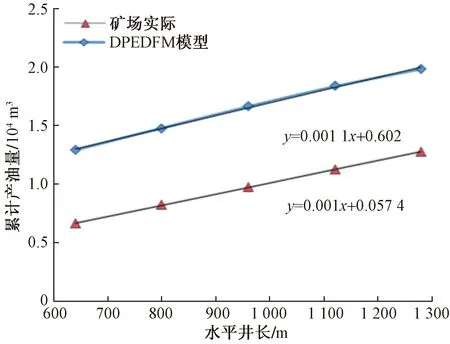
图12 不同水平井长度生产2 000 d时累产油图Fig.12 Cumulative oil production maps for 2 000 d at different horizontal well lengths

图13 不同水平井长度生产2 000 d时采收率图Fig.13 2 000 d recovery maps for different horizontal well lengths

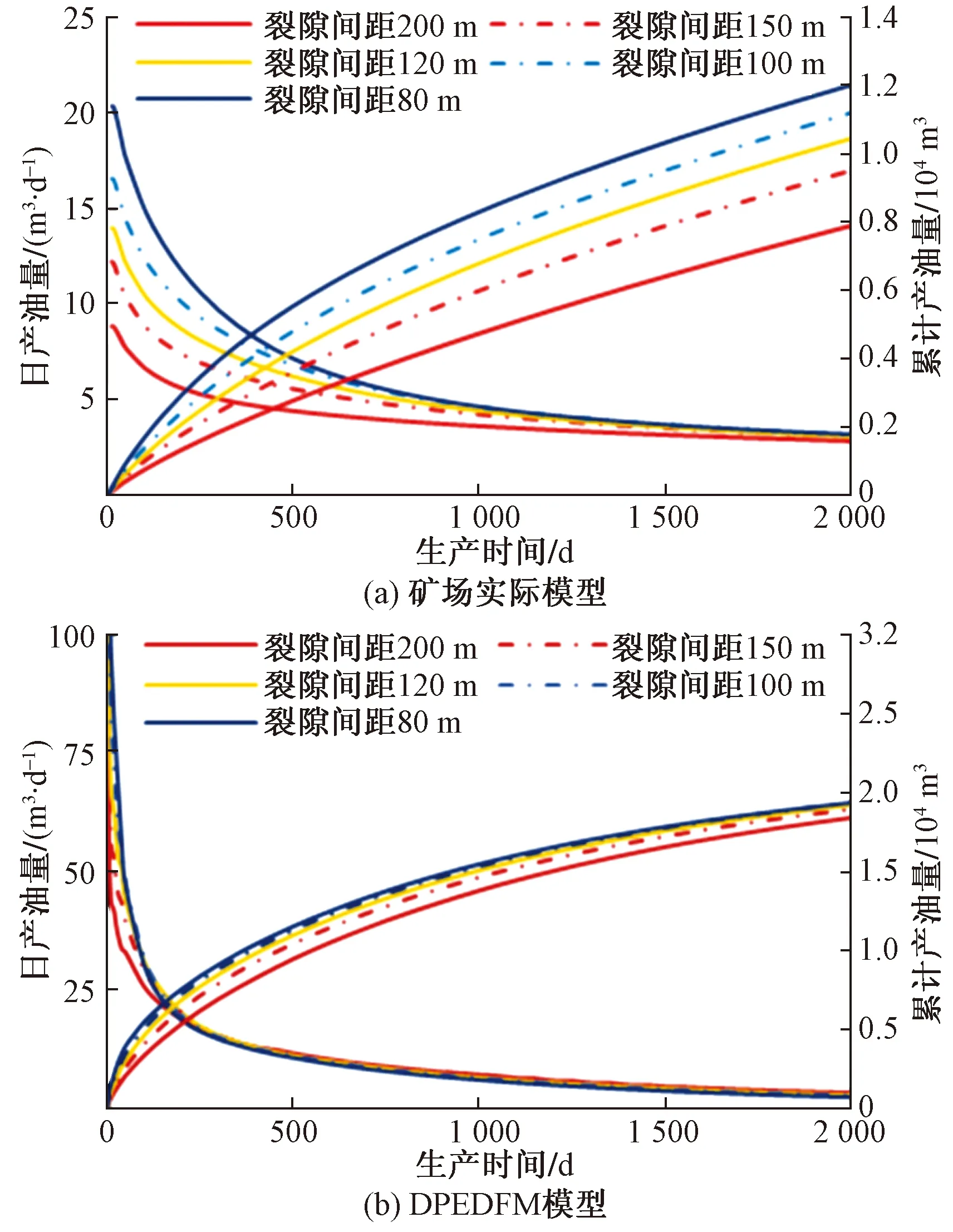
图14 不同裂缝间距时产能图Fig.14 Productivity comparison diagram at different fracture spacing

2.3.2 人工裂缝间距对产能的影响

水平井人工裂缝间距是开发方案设计时需要考虑的重要问题[33-34]。以矿场实际模型与DPEDFM模型为例,研究了裂缝间距对产能的影响。设置水平井长度为1 200 m,分别设置裂缝间距为200、150、120、100、80 m进行模拟,矿场实际模型中SRV区为1 300 m×220 m矩形,SRV区中心与模型中心相重合,模拟结果如图15所示。

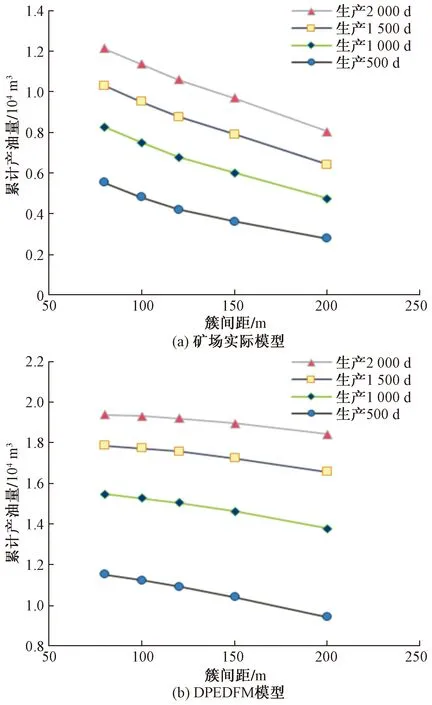
图15 不同生产时间和裂缝间距下累计产油量对比Fig.15 Comparison of cumulative oil production under different production time and fracture spacing

模拟结果表明,裂缝间距越小,在整个生产周期内,累计产油量越高。开井生产1 000 d以后,不同模型累计产油量之间的差距并未进一步扩大。在生产前期,裂缝间距越小,日产油量下降速度越快,以矿场实际模型为例,如图14(a)所示,在开井生产前1 000 d,裂缝间距为200 m的模型日产油量从8.89 m3/d降至3.62 m3/d,裂缝间距为80 m的模型日产油量从20.29 m3/d降至4.61 m3/d;开井生产1 000 d以后,不同裂缝间距下日产油量变化较小,且各裂缝间距日产油量之间的差距逐渐缩小,其原因在于,生产前期,小间距裂缝可以较好地改善近井地带流体渗流能力,改造区内原油通过SRV区内裂缝渗流至水平井内;生产中期,改造区原油开采殆尽,产能主要依赖未改造区域渗流。

2.4 应力敏感

天然裂缝作为致密油藏生产时的重要渗流通道,有必要开展应力敏感效应对产能影响分析。以矿场实际模型为例,设置水平段长1 200 m,裂缝条数定为7条,SRV区与2.3.2节中的矿场实际模型相同,基质中不考虑应力敏感,分别模拟天然裂缝应力敏感系数在0、0.01、0.02、0.03 MPa-1下的生产情况。选取SRV区中一点,分析在生产时间为500、1 000、1 500、2 000 d时该点的渗透率、压力变化情况,结果如图16和图17所示。

图16 产能对比图Fig.16 Production capacity comparison chart

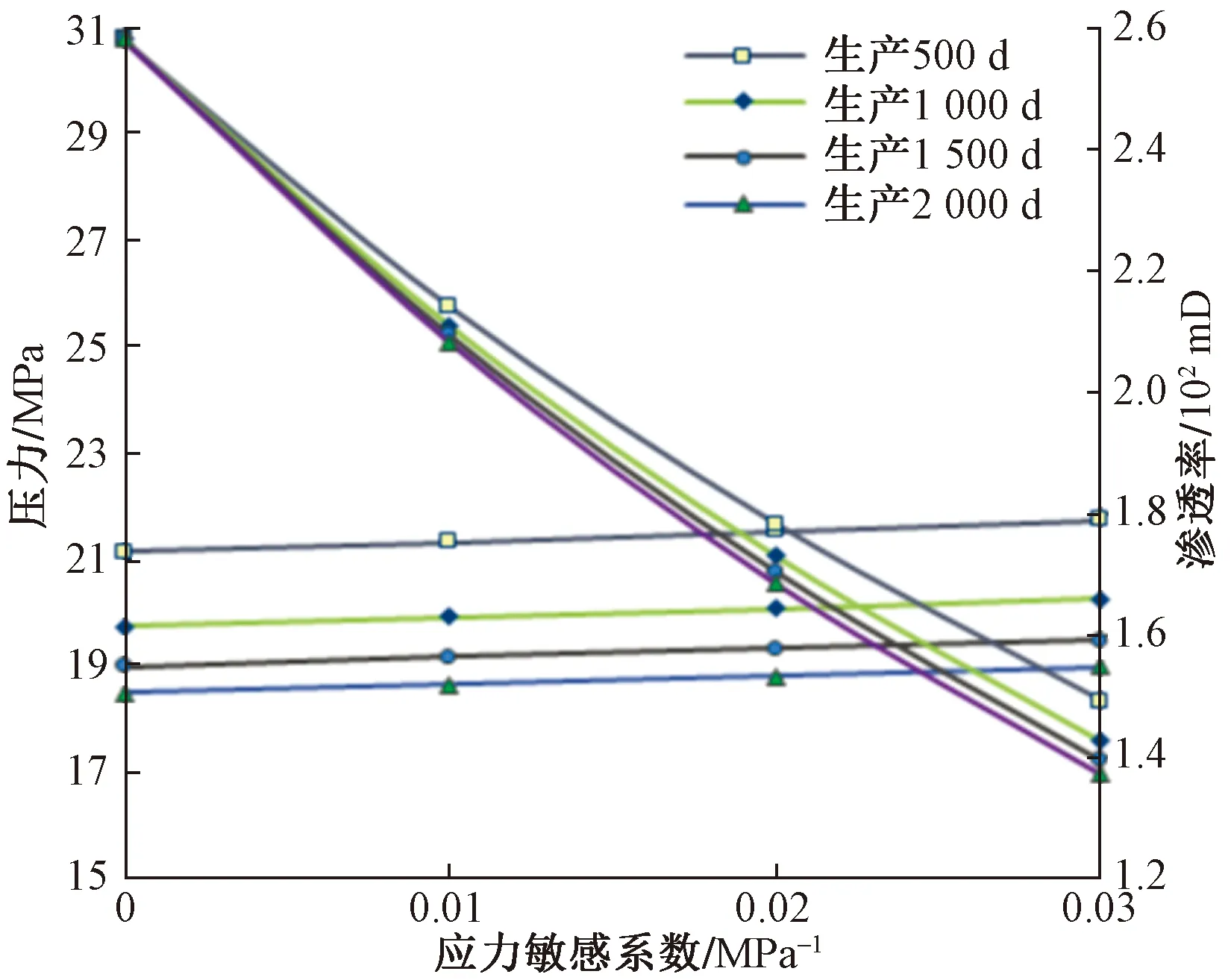
图17 日产油量对比图Fig.17 Daily oil production comparison chart

模拟结果表明,应力敏感系数越大,累计产油量越低,日产油量越低,且随着生产的继续,应力敏感对油藏产能的影响先增大后逐渐缩小,具体体现为图16中,应力敏感系数为0 MPa-1与0.03 MPa-1的模型生产1 d时日产油量相差0.21 m3/d,生产50 d时相差0.99 m3/d,生产500 d时相差0.65 m3/d,生产2 000 d时相差0.30 m3/d。其原因在于,各模型初始渗透率相同,开井生产初期,日产油量较大,改造区压降速度快,渗透率下降速度大;随着生产的继续,日产油量逐渐降低,改造区压降速度变慢,渗透率下降速度变慢。

3 结论

提出了适用于致密油藏流动模拟的数学模型,该模型在精细刻画天然微裂缝、基质和水力裂缝复杂传质机理的基础上兼具了计算速度快的优点。基于所建立模型编制数值模拟器,并使用商业软件Saphir、Petrel验证了模型的正确性。使用模拟器研究了天然微裂缝属性体、水平段长度、人工裂缝间距等多因素对致密油藏水平井产能的影响规律,得出以下结论。

(1)在致密油藏中,天然裂缝对流体渗流至关重要。在模拟过程中,考虑了天然微裂缝属性体的DPEDFM模型计算得到的日产量、累计产量和储层压力下降速度均高于传统EDFM模型。

(2)同一参数下的DPEDFM模型与EDFM模型在生产一定的时间后累计产水量相等,且DPEDFM模型产水速度下降更快。

(3)水平段长度与产能之间为正相关近似线性关系。不同模型增长相同水平段长时获得的累计产油量、采收率均不相同,因此在实际应用时应基于实际模型进行最佳水平井长的选取。

(4)裂缝间距对产能有一定影响,随着人工裂缝间距逐渐缩小,产能逐渐增大,动用油藏能量的能力越强。不同人工裂缝间距下产能之间的差异先增大后减小。减小裂缝间距对提升生产初期的产能效果明显,但对生产中后期的产能影响不明显。

(5)应力敏感效应会导致水平井产能下降,应力敏感系数越大,产能下降越快;且应力敏感对产能的影响随着开井生产时间的增加先增强后减弱。对于应力敏感较强的储层,建议采用注水、气进行开发,以达到稳产的目的。