圆弧形聚能装药结构爆破破岩效果数值模拟
张文明, 汪海波*, 李万峰, 姜自亮, 宗琦
(1.安徽理工大学土木建筑学院, 淮南 232001; 2.淮南矿业(集团)有限责任公司, 淮南 232001)
炸药的聚能效应就是在传统药包的一端形成一个聚能穴,这个穴将炸药爆炸产生的能量集中聚集,产生定向爆破的威力[1]。关于炸药的聚能现象,早在18世纪就发现了在药包的一端有空穴结构,炸药在起爆后会在一定的范围内聚集能量。关于高能炸药的“空穴效应”,是德国的冯·福斯特(von Foerster)率先提出的,他发现爆破能量可以通过空心凹穴汇聚形成聚能射流,形成的射流具有明显的侵彻效应,这是对“空穴效应”的第一个全面解释[2]。在聚能装药结构方面进行了大量的研究,例如在物理实验方面,杨仁树等[3]研究了切缝装药包的定向断裂控制爆破机理,分析了不同装药结构下爆生气体产生裂缝的主要特征,对比了主、次裂纹的动态能量释放率的异同。左进京等[4]分析了含有预制裂缝的空心孔在爆炸荷载作用下的力学响应。在数值模拟方面,基于流元法,黄涛等[5]模拟了双炮孔破岩,展现了裂纹的产生和演化、块体和爆破漏斗的形成。刘兵兵等[6]使用ANSYS/LS-DYNA,建立了水下钻井爆破数值模拟模型。分析了水下岩体在不同起爆方式和不同封堵材料下的钻爆效果,分别得到了水下岩体的压力时程曲线、速度时程曲线和垂直应力时程曲线。吴波等[7]研究了不同聚能管材料下双向聚能装药结构爆炸后随锥角的变化规律,对比了椭圆形外壳、直线形外壳和椭圆+直线形外壳3种形状的聚能射流效果。杨建辉等[8]对切缝药包聚能管壁厚分别为1、2、3、4 mm以及切缝宽度分别为 1、2、3、4、5、6、7 mm的工况进行了模拟,对各个工况下的应力变化进行了对比。李宏伟等[9]通过数值模拟研究了孔距对角岩爆破裂缝扩展的影响,结果显示,孔距的增加有助于孔周围裂缝的充分扩展,并在现场得到了验证。李必红等[10]用实验的方法对不同孔径的侵蚀效应进行拟合,并用LS-DYNA对不同工况进行模拟,得出了最优不耦合系数。赵根等[11]以环向聚能药包作用原理为基础,对聚能爆破致裂岩石的影响因素进行了深入研究,并成功地将自行研制的射孔型和切割型两种环向聚能药包用于现场。何满潮等[12]对巷道顶板预裂的炮孔间距进行了现场实验,得出了最佳间距,结合数值模拟验证其可靠性。
传统的聚能穴截面多为三角锥形,射流为线形,以造成被爆介质的破裂、贯穿。对于隧(巷)道掘进爆破,单一的贯穿裂纹并不利于槽腔岩石的破碎和抛掷。因此,现提出采用圆弧形聚能穴以减小单个裂纹长度、增大裂纹数量和破裂范围。研究聚能掘进爆破炮孔和药卷尺寸,利用ANSYS/LS-DYNA有限元软件,建立4个圆弧形聚能穴装药爆破几何模型,以期通过对比分析确定出最佳参数。
1 计算模型与参数
1.1 模型计算方案的选取
根据煤矿巷道掘进所用钻头直径和炸药药卷直径大小,炮孔直径采用42 mm,聚能装药结构为圆弧形,采用PVC材料、管壁厚度为1 mm,整个PVC管内壁直径为38 mm,外壁直径为40 mm,以满足顺利装入炮孔的需求。圆弧形凹槽半径为10 mm,聚能穴内边缘至管中心距离d分别为6、8、10、12 mm,如图1所示。

图1 不同工况聚能参数模型Fig.1 Models of different shaped energy parameters
使用ANSYS软件进行前处理建立模型,然后在LS-DYNA添加约束和计算,最后用LS-PREPOST导出数据,进行数据与曲线的处理。模型采用solid164实体单元。模型的尺寸厚度为1 mm,既可以减少计算时长,也能清晰地展现爆破效果。其中岩石采用Lagrange 网格建立圆形模型,空气和炸药采用Ale 网格建模,整体采用流固耦合算法。具体建立模型如图2所示。
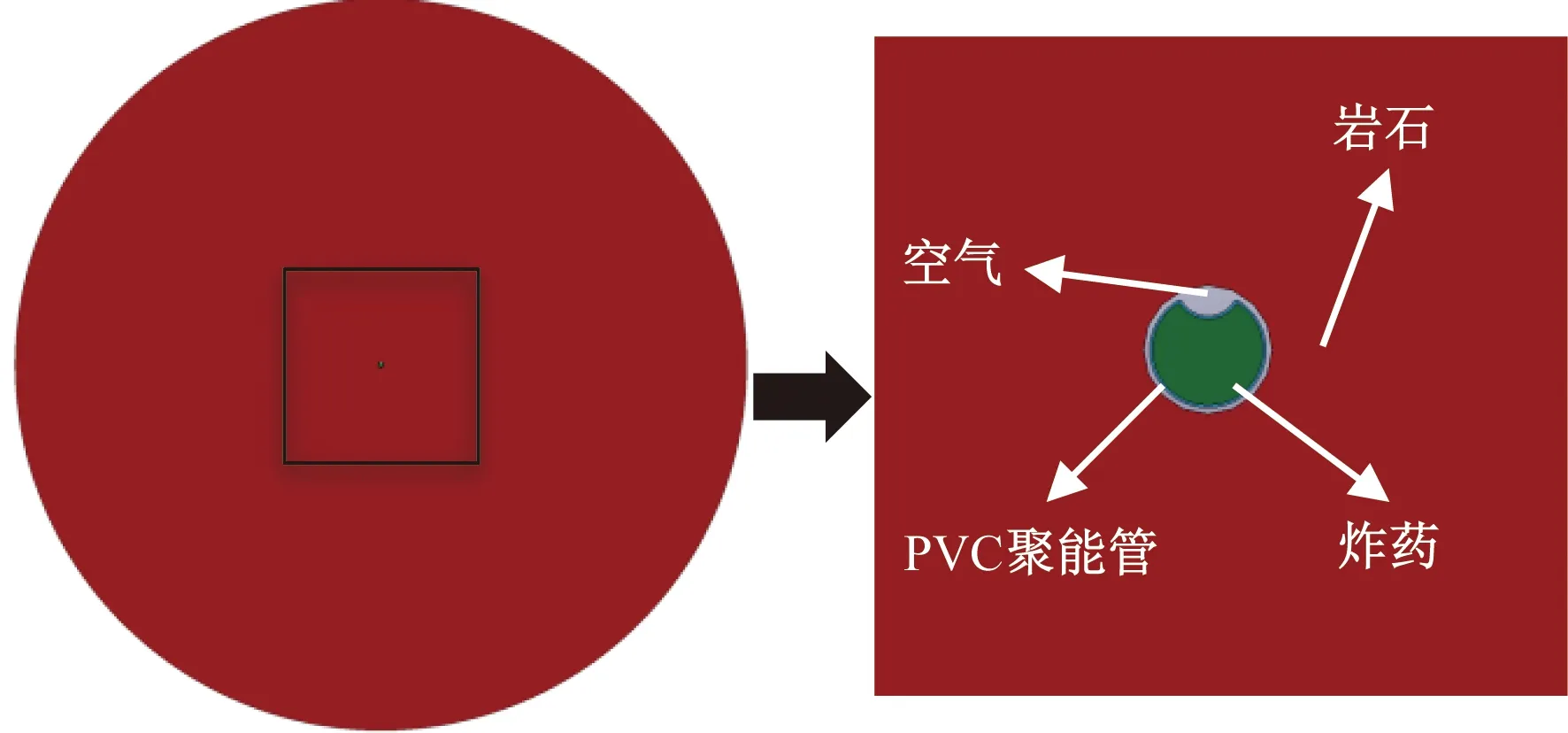
图2 计算模型Fig.2 Computational model
1.2 计算参数的选取
炸药采用*MAT_HIGH_EXPLOSIVE_BuRN材料模型,状态方程通过关键字*EOS_JWL 进行定义,炸药材料及状态方程参数见表1[13]。

表1 炸药材料及状态方程参数Table 1 The parameters of explosive material and state equation
JWL状态方程为
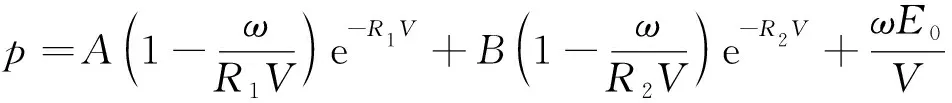
(1)
式(1)中:p为方程确定的爆轰压力。
空气采用*MAT_NuLL 空白材料模型,并同时使用*EOS_LINEAR_POLYNOMIAL 线性多项式描述其状态方程为
p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E
(2)
式(2)中:p为爆轰压力;C0~C6为常数;E为单位体积的内能;μ为相对体积简化式。空气本构参数及状态方程参数见表2[14]。

表2 空气材料参数Table 2 Air material parameters
岩体材料模型采用*MAT_JOHNSON_ HOLMQUIST_CONCRETERHT,本构参数及状态方程参数见表3[15]。
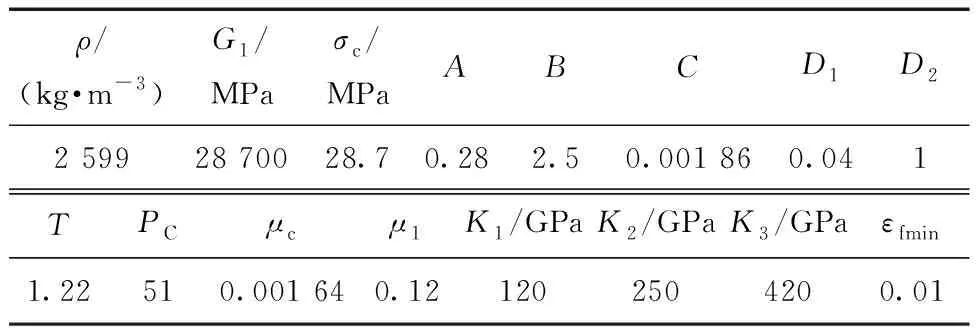
表3 岩体 JHC 模型参数Table 3 Parameters of JHC model for rock mass
聚能管采用PVC材料,PVC材料是一种热塑性材料,经过高温后会发生相变分解成HCl气体,由于爆炸是一个非常迅速的过程,爆炸所产生的爆轰波和爆生气体会用极短的时间使PVC管形成聚能射流,在这一瞬间可认为PVC材料发生了形变并未发生相变,故PVC 材料可选用随动硬化模型 MAT_PLASTIC_KINEMATIC来表征材料的力学变化,PVC聚能管物理力学参数见表4[16]。

表4 PVC聚能管物理力学参数Table 4 Physical and mechanical parameters of PVC shaped charge pipe
2 数值模拟结果分析
2.1 裂纹演化过程
为了研究岩体在爆炸后的裂纹发展情况,通过在k文件中添加*MAT_ADD_EROSION 单元失效关键字[17],将聚能穴内边缘至管中心距离为12 mm岩石模型的拉、压强度参数定义为单元失效阈值,从而能够直观地看到裂纹的演化和发展情况。
根据图3可以看出,在20 μs处,爆炸应力波接触到孔壁,所产生的径向压缩作用使得孔壁附近的岩体开始出现破碎,这时由于爆炸的时间较短,还没有出现明显的聚能现象。到40 μs时,在聚能管的作用下,爆炸应力波集中在聚能方向,裂纹开始沿着聚能方向发展,岩体的聚能方向开始出现一些细小裂纹。100 μs时爆炸应力波使得炮孔周围的细小裂纹更加绵密,爆生气体沿着细小裂纹进入裂纹表面产生的压缩作用,使得聚能方向的裂纹不断扩展。随着爆炸应力波的传播,裂缝逐渐扩展,直到350 μs,爆生气体沿着之前的裂纹进入岩体发生气楔作用,使得裂纹进一步扩展。到600 μs时爆炸应力波到达模型的边界,产生的反射拉伸波对裂纹的再次作用,爆炸应力波与反射拉伸波共同作用下在边界附近产生了一圈环向裂纹。但在反射拉伸波到达裂纹末端时,对裂纹表面形成的拉伸作用使得裂纹沿反射拉伸波传播方向进一步扩展。

图3 工况四爆破后岩体裂纹的演化情况Fig.3 Evolution of crack in rock mass of the fourth working condition
通过更改另外3个工况的k文件得到其裂纹发展情况,这里将4个工况以及无聚能装药结构的裂纹发展的第400 μs的岩体裂纹发展情况做对比来比较不同装药参数下的聚能效果,如图4所示。
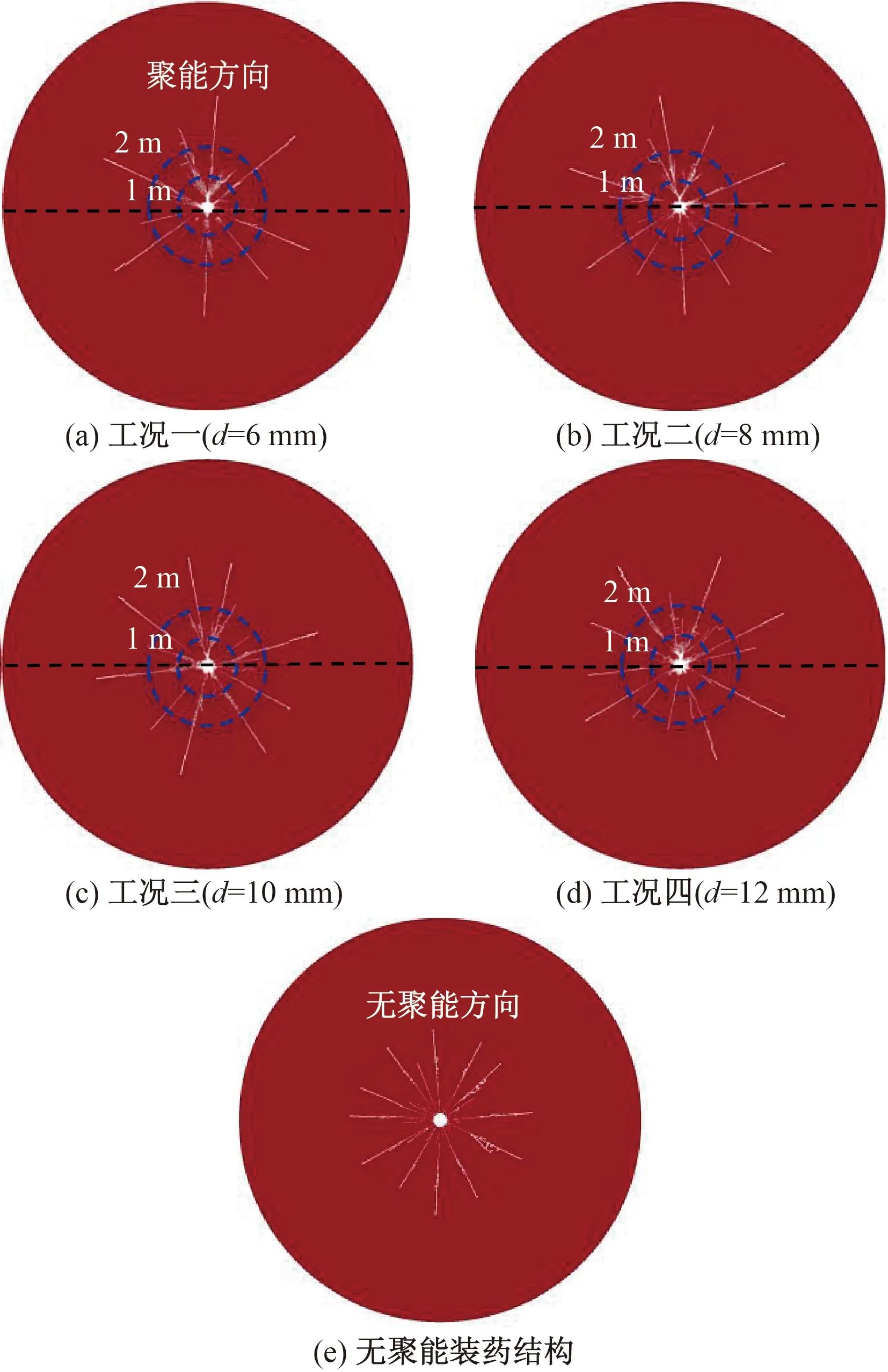
图4 不同聚能装药结构的岩体裂纹分布Fig.4 Rock fracture distribution with different polyenergy charge structures
由图4可以看出,将图4(e)与图4(a)~图4(d)做对比发现,有聚能装药结构的工况在聚能方向失效岩石单元的密集程度明显都多于无聚能装药结构,说明4种聚能装药结构都有一定的聚能效果。在爆炸后炮孔周围1 m范围内,在聚能方向图4(d)的失效岩石单元的密集程度较其他3个工况更加密集。在爆炸后炮孔周围2 m范围内,图4(c)的爆生主裂纹为6条,较图4(a)增加3条,较图4(b)增加1条,较图4(d)减少1条。分析认为导致这种现象的主要原因是在爆炸后在聚能装药作用下,爆炸应力波在聚能方向较非聚能方向产生更多细小裂纹,爆生气体沿着爆炸初期的细小裂纹传播,逐步发展成主裂纹。而在这一过程中由于各个工况聚能效果的差异,导致爆炸应力波在聚能方向使得岩体产生的细小裂纹数量也存在差异,在爆生气体的作用下使得聚能方向和非聚能方向的主裂纹的数量出现了差异。
2.2 有效应力分布特征
为了更加清晰地确定4种不同工况的聚能效果,以模型的炮孔中心为坐标原点,定义y轴的正方向为聚能方向,负方向为非聚能方向。在聚能方向和非聚能方向选取距炮孔中心15、25、35、45、55 cm的单元,通过LS-PREPOST后处理导出各个工况的相关数据,得到各个工况第一主应力峰值及聚能穴内边缘至管中心距离12 mm时有效应力随时间变化曲线图,如表5、图5所示。
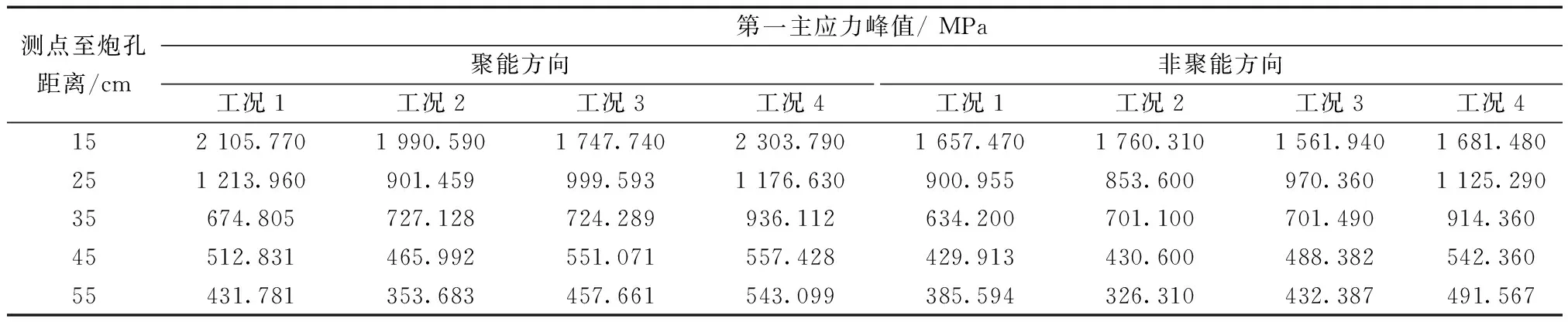
表5 不同工况下第一主应力峰值统计表Table 5 Statistics of the first main stress peak under different working conditions

图5 工况四炮孔周围有效应力时程曲线Fig.5 Time course curve of effective stress around the fourth working condition gun hole
由表5、图5可以看出,随着至炮孔中心距离的增大,应力峰值在初期迅速增大而后逐渐衰减。对于非聚能方向,爆炸初期,也就是在0~200 μs时,爆炸能量在岩体中迅速蔓延,使得岩石的有效应力快速增加,并达到峰值。随着爆炸应力波的传播,在200 μs后炸药释放的能量不断被消耗,岩石受到的有效应力不断减小并逐渐趋于平稳。对于聚能方向,在0~100 μs内,炮孔周围岩体受到爆炸应力波的作用,有效应力会迅速增加,由于时间很短,聚能管还未被破坏,导致爆炸应力波的能量在聚能穴处聚集,使得聚能方向的有效应力值在前50 μs会明显大于非聚能方向,直到增加到应力的最大峰值。100 μs后聚能管已经破坏,对炸药形状几乎没有了约束作用,聚能效应明显下降,爆炸应力波在岩体中不断衰减,有效应力也会逐渐下降。但随着爆炸的进行,岩体中爆炸应力波发生叠加,使得在100~200 μs出现短暂的震荡期,即峰值后应力不再单调递减,而是类似于脉动应力。在200 μs后,聚能现象已经消失,爆炸应力波没有了叠加作用而不断衰减,有效应力也随之下降最后趋于平稳。
结合表5、图5可以得出:4个工况在爆炸后均出现了较为明显的聚能效果。其中聚能穴内边缘至管中心距离6 mm和聚能穴内边缘至管中心距离12 mm的聚能效果明显大于聚能穴内边缘至管中心距离8 mm和聚能穴内边缘至管中心距离10 mm。通过图5(b)可以看出,爆炸的有效应力到达峰值后聚能穴内边缘至管中心距离为6 mm有效应力的平稳值在220~410 MPa,较聚能穴内边缘至管中心距离为12 mm有效应力的平稳值增加60~135 MPa,说明爆炸后炸药能量分配到非聚能方向能量距圆心6 mm偏多。
进一步得到不同工况下岩体的有效应力峰值随距离的衰减关系以及峰值变化规律,如图6所示。

图6 各个工况下不同位置有效应力峰值的变化情况Fig.6 Variation of the peak effective stress at different positions under each working condition
由图6(a)所示,随着距炮孔中心距离不断增加,应力波在岩体中会逐渐衰减,导致有效应力峰值会不断减小。对比4个工况聚能方向的有效应力峰值可以看出:4个工况的聚能方向的有效应力峰值明显大于非聚能方向。其中聚能穴内边缘至管中心距离为12 mm的有效应力峰值最大,约为2 303.5MPa。
在距炮孔15 mm处,对于聚能穴内边缘至管中心距离为6 mm的聚能方向和非聚能方向,峰值相差约为211.2 MPa,对于聚能穴内边缘至管中心距离为8、10、12 mm峰值相差分别约为230.3、125.58、622.31 MPa。这4种工况峰值差值先减小后增加,从聚能穴内边缘至管中心距离为6 mm到8 mm峰值差值减小,由于装药结构发生变化,导致有效装药量发生改变。在聚能穴内边缘至管中心距离为10 mm到12 mm峰值差值增加,其主要原因是因为聚能穴内边缘至管中心距离12 mm的单位装药量为10.47 cm3,相比之前3个工况单位装药量分别增加了1.22、0.79、0.38 cm3,随着药量的增加,使得药量的作用超过了聚能穴内边缘至管中心距离变化的作用。
结合图5、图6(b),在与炮孔中心距离相同的情况下,到达有效应力峰值的时间先增大后减小,有效应力时程曲线斜率先减小后增大。以距炮孔中心距离15 cm聚能方向为例,聚能穴内边缘至管中心距离6 mm到达有效应力峰值的时间为53.5 μs,曲线斜率为39.36。较之聚能穴内边缘至管中心距离8 mm曲线斜率减小13.3%,较之聚能穴内边缘至管中心距离10 mm曲线斜率减小27.7%,而较之聚能穴内边缘至管中心距离12 mm曲线斜率增加17.3%。
2.3 岩体的损伤演化
当炸药发生爆炸时,能量在前200 μs聚能现象较为明显,在不添加失效准则时把炮孔周围聚能穴内边缘至管中心为12 mm时前200 μs的岩体损伤演化历程展示如图7所示。
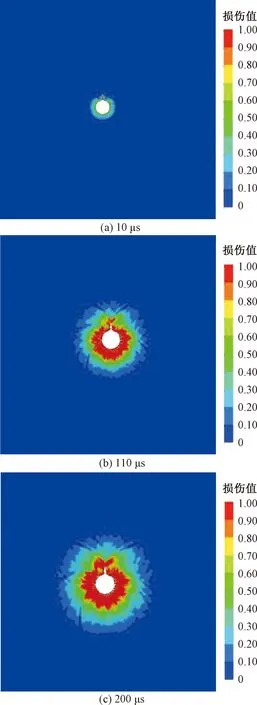
图7 工况四岩体损伤云图Fig.7 Rock damage cloud map of the fourth working condition
数值模拟中通过损伤值H(0 为了进一步比较不同工况炮孔周围岩体损伤程度,以距炮孔周围15 cm时聚能方向和非聚能方向为测点,得到4种工况前500 μs的损伤时程曲线如图8所示。 图8 不同工况下的时程损伤值Fig.8 Amount of time-range damage at different working conditions 由图8可以看出,对于聚能方向,聚能穴内边缘至管中心距离6、8、12 mm的损伤值都达到了1,表明岩体最终完全损伤破坏。对比聚能穴内边缘至管中心距离6、8、12 mm发生完全损坏的时间可知,聚能穴内边缘至管中心距离12 mm率先达到损坏,聚能穴内边缘至管中心距离6 mm次之,说明聚能穴内边缘至管中心距离12 mm在爆炸后能量迅速向聚能方向发展,导致岩体在聚能方向受到较大的爆炸应力波,使得岩体先于非聚能方向达到完全损伤破坏,相对其他工况聚能效果最佳。 对于非聚能方向,4种工况的损伤值均未达到1,即所取测点的岩体未发生完全损伤破坏。聚能穴内边缘至管中心距离6 mm的损伤值为0.61,分别是聚能穴内边缘至管中心距离8 mm损伤值的1.11倍,聚能穴内边缘至管中心距离10 mm的1.65倍,聚能穴内边缘至管中心距离12 mm的1.09倍。 对于聚能方向和非聚能方向,聚能穴内边缘至管中心距离6~12 mm 4个工况的损伤值差值分别为0.63、0.45、0.47、0.44。综上所述,聚能穴内边缘至管中心距离12 mm的岩体损伤程度最大,聚能穴内边缘至管中心距离6 mm次之。 岩石的内部结构复杂多变,且岩石的力学性质除受到岩性影响外,还受应力状态、受载荷作用时间等因素的影响。而在模拟仿真的过程中,岩体模型不可能完全真实地反映岩石特性,使得模拟计算会产生一定的误差,但根据实验目的不同,可进行针对性的简略。为了探究不同聚能装药结构的聚能效果,通过岩体模型的裂隙演化进行对比分析,而为了让裂隙演化更加真实可靠,对岩体单元的大小进行了多次验证并进行了数值收敛实验,直到两个相邻试验模拟结果的差值减小到5%,使得实验结果更加符合真实情况。 (1)在裂纹定向扩展方面,圆弧形聚能装药结构可以明显增强聚能方向的爆炸能量,对岩体裂纹的扩展起到导向作用。 (2)随着聚能穴内边缘至管中心距离的增加,岩体的有效应力峰值出现先减小再增大的现象。反映了聚能药包的聚能效果不仅与聚能穴内边缘至管中心距离有关系,还与有效装药量存在一定关系。 (3)聚能穴内边缘至管中心距离为12 mm的聚能药包在距炮孔15 cm处最先且最快达到完全损伤破坏,相对于其他工况岩体损伤程度最大。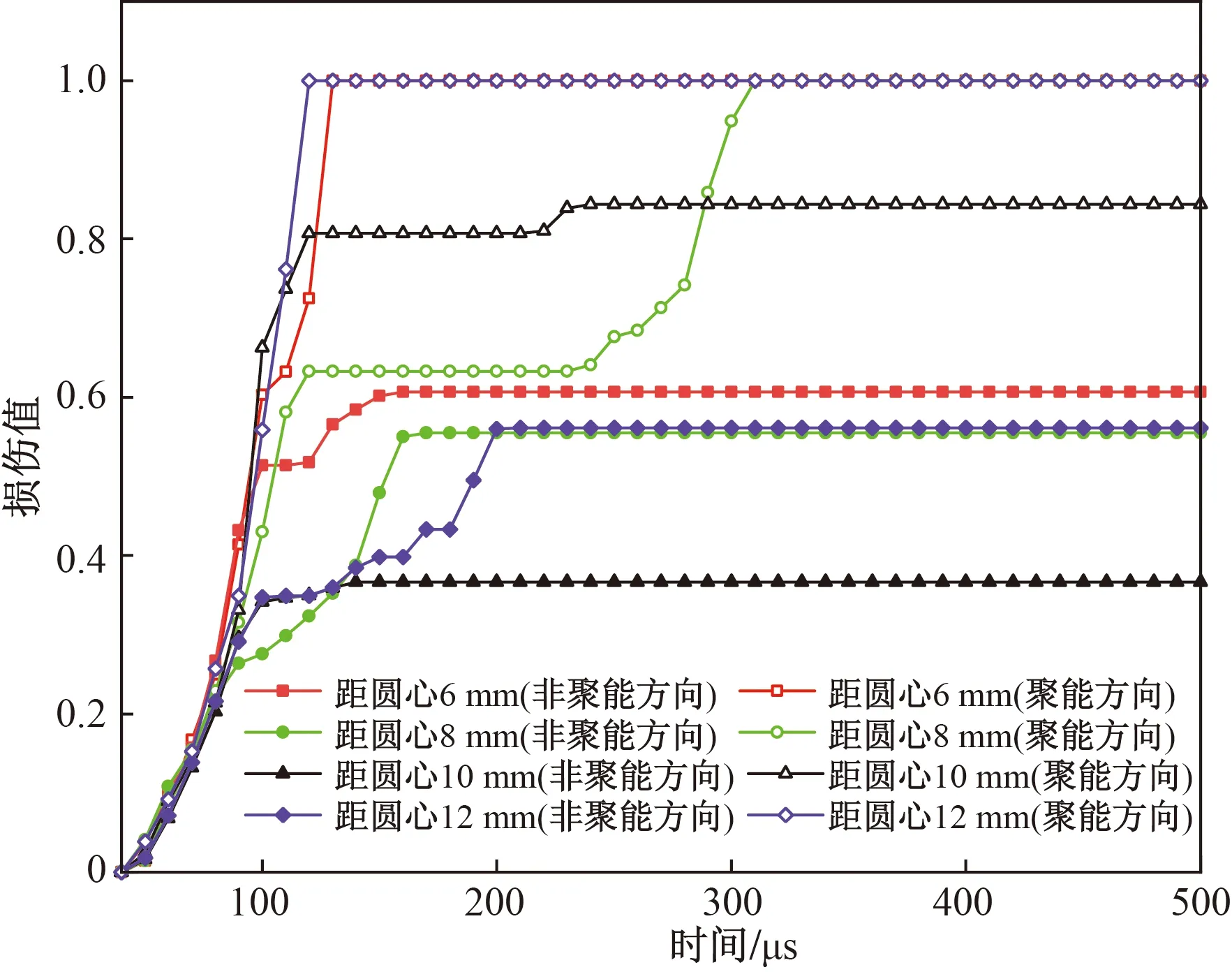
2.4 模拟有效性和误差分析
3 结论

