概率犹豫模糊环境下基于累积前景理论和VIKOR的多属性群决策方法
王志平, 张梦, 傅敏, 王沛文
(1.大连海事大学理学院, 大连 116026; 2.大连海事大学航运经济与管理学院, 大连 116026)
多属性决策作为现代决策科学的一个重要组成部分[1]正在被应用于生活中多个领域。而考虑了多个观点的多属性群决策方法的研究变得日益重要,特别在信息模糊性和犹豫决策这两个方面[2]。
语言模型在多属性群决策中是非常重要的[3]。由于外部环境的复杂性和信息的模糊性,在现实中很难准确客观地评价。犹豫模糊集作为模糊集的扩展,在可能有多个值时确定隶属度。然而,缺点是假设犹豫模糊元素中每个隶属度的出现概率相等[4]。此后,2017年,Xu等[5]改进犹豫模糊集并提出犹豫概率模糊集,为隶属度添加了概率信息,更准确地描述了决策信息。在此基础上,逐步有学者提出犹豫概率模糊环境下的距离度量定义[6],构建犹豫概率模糊集的得分函数、偏差函数和比较规律[7]。
继提出前景理论[8]后,后悔理论[9]、失望理论[10]、累积前景理论[11]等心理行为决策理论相继提了出来。其中,累积前景理论创新了价值函数和权重决策函数,将累积概率代替单个概率,弥补了前景理论的不足,目前已经得到了有效应用。例如闫书丽等[12]运用累积前景理论解决动态风险灰靶决策问题;高建伟等[13]将累积前景理论用于概率犹豫模糊集的多属性决策问题。
关于累积前景理论在概率犹豫模糊环境中的研究鲜少。有的部分研究模型过分考虑决策者主观心理因素,而忽略了客观求解的影响,同时在排序方式上也很主观,导致结果并不够理性。基于折衷优化思想提出多准则妥协优化解[14](VIKOR)排序方法,克服了传统方法中方案排序方式的局限,并具有同时考虑群体效用最大化和个体遗憾最小化以及融入决策者主观偏好的优点。因此,现基于概率犹豫模糊环境,构建主客观结合模型,进行多属性决策问题研究。
综上所述,现提出在概率犹豫模糊环境下,基于累积前景理论的VIKOR多属性决策方法模型。首先,用概率犹豫模糊语言规范法则对初始信息进行规范化处理,同时利用群体一致性原则对决策者权重系数进行调节,使评估结果更加接近事实;其次,通过最小相对熵原则,主客观结合求取整体属性权重,不仅让权重计算更简便,也更合理;再次,利用累积前景理论,构建正、负价值矩阵和权重矩阵,进而得出更加理性的正、负理想解矩阵;然后创新性地将累积前景理论和VIKOR法相结合进行排序择优;最后和其他方法的结论进行比较和分析,验证所提方法的可行性与合理性。
1 理论基础
1.1 概率犹豫模糊集
定义1[15]给定任意非空集合X,则定义在有限集合X上的一个概率犹豫模糊集可以表示为
H={〈x,h(p)|x∈X}
(1)

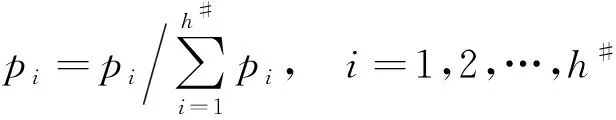
(2)
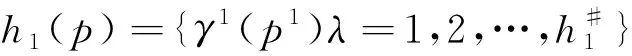

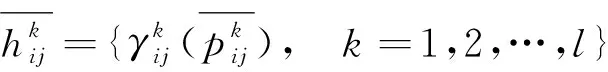
(3)
定义4[19]设h1(p)和h2(p)是两个概率犹豫模糊集,如果两个模糊集的元素数量相同,则同时给出两个概率犹豫模糊集的坎贝拉距离测度公式为
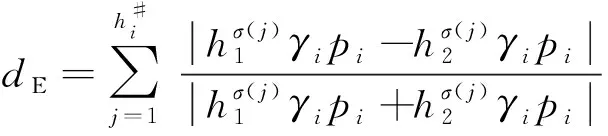
(4)

定义6[20]设h(p)是一个概率犹豫模糊集,其得分函数定义为

(5)
基于得分函数,其偏差度函数可以定义为

(6)
在得分函数和偏差度函数的基础上,任意两个概率犹豫模糊元h1(p)和h2(p)可按照以下原则进行比较。
(1)如果s1[h(p1)]>s2[h(p2)],则h1(p)>h2(p)。
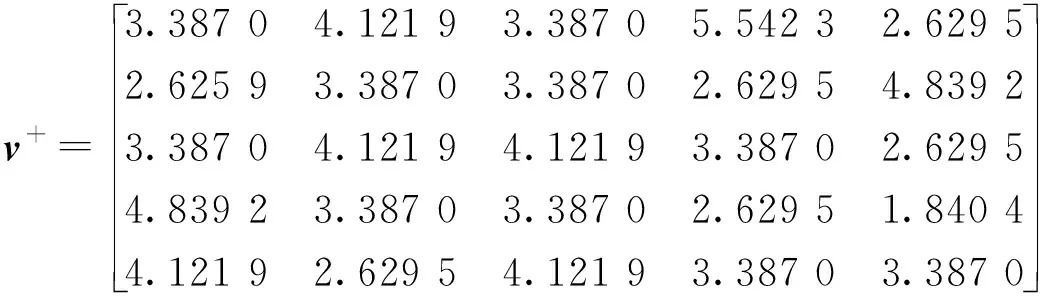
(2)如果s1[h(p1)] (3)如果s1[h(p1)]=s2[h(p2)],且d1[h(p1)]>d2[h(p2)],则h1(p) Tversky和Kahneman提出的累积前景理论[11],允许损失和收入有不同的权重函数,并通过累积的概率代替单个概率计算概率权重,满足一阶随即占优,将适用范围扩展,同时适用于风险决策和不确定决策,是行为决策理论中的标志性理论。累积前景价值的计算主要由两部分构成,即价值函数和决策权重函数,公式如下。 (7) 价值函数体现了决策者在面临收益时更倾向于风险规避以及面临损失时更倾向于风险追求的特性,即 (8) 价值函数的值是基于每个备选方案距离参考点的收益或损失的距离。因此,关键是选择一个合适的参考点,通常情况下,选取数据的中间值、期望、积极和消极的解作为理想参考点。分别选取备选方案与正、负理想点之间的距离作为参考来得到偏差程度 (9) (10) (11) 式中: (12) (13) 式中:δ为风险收益态度系数;ε为风险损失态度系数,且0<δ,ε<1。 表1 决策者k的决策矩阵Table 1 Decision matrix of decision maker k (14) (15) 很显然,ρk表示的是决策者dk与其他决策者的一致性程度,即决策者dk提供的评价信息在整个评价小组中的受支持程度。同时反映了决策者dk的重要性。在某种程度上来讲,如果dk越重要,相应的调节系数ρk越大,那么决策者dk权重应当适当增加。因此,由事先赋予的主观决策者权重ηk和调节系数ρk来最终确定决策者权重,公式为 (16) 通过主客观结合的方式确定整体属性权重,构造了两个模型来分别获得客观属性的权值和整体属性的权值。首先进行客观部分的求解,然后考虑主观因素确定整体属性权重。 2.3.1 基于得分函数客观权值的确定 对于实际应用中的多属性决策问题,得分函数通常被认为是描述概率犹豫模糊集中信息特征的有效工具。然而,当两个概率犹豫模糊集的分数值相同时,需要区分它们。为了克服这一缺点,基于平均值和犹豫度的犹豫模糊语言元素的得分函数可以完全反映概率犹豫模糊集的分散度和特征,而不必在决策过程中分离绑定的值[21]。其公式为 (17) 考虑到概率犹豫模糊环境下多属性决策情况的复杂性,基于得分函数,进一步得出客观属性决策模型为 j=1,2,…,n (18) 2.3.2 基于最小相对熵原理的总权重确定模型 实际上,决策者通常在属性值及其重要性上有所不同,而且每个决策者的权重都会取决于个人判断而有所不同。因此,综合所有决策者对属性权重和客观的决策信息的评价是很重要的。采用一种基于最小相对熵原理[15]的合适而有效的方法进行了主观和客观属性的权值进行结合。该方法不仅考虑了所有决策者的意见,还考虑了决策者权重和客观的决策信息,公式为 j=1,2,…,n (19) 针对在属性权重、专家权重都未知的情况下,利用群体一致性调节法和基于最小相对熵原理的主客观相结合法对决策者、属性权重进行求解之后,提出了一种基于累积前景理论和VIKOR法进行结合的排序方式,来解决多属性群决策问题,利用以下步骤构建整体算法模型,技术路线图如图1所示。 图1 技术路线图Fig.1 Technology roadmap 步骤3通过式(17)~式(19),利用主客观结合的思想求得属性权重ω=(ω1,ω2,…,ωn)T,即通过式(17)求出得分函数,基于得分函数继而求得客观属性权重,最后基于最小相对熵原理得到总权重信息。 (20) (21) 步骤5利用式(10)~式(13)求出决策权重值后,得到累积前景价值矩阵,公式为 (22) 步骤6利用VIKOR法进行综合排序。 (1)通过式(23)、式(24)确定正负理想前景价值。 (23) (24) (2)利用式(25)和式(26)计算群体效益值Si、个体遗憾值Ri和利益比率Qi。 (25) (26) (27) (3)根据Qi、Ri、Si由小到大的顺序对备选方案进行优劣排序,Qi、Ri和Si的值越小,方案越优。 实例源自文献[15],假设先有几个车辆专家对几款车的安全性能进行评价排序;别克A1、丰田A2、福特A3、奥迪A4、特斯拉A5,对这5款车选取了能够反映其安全性能的5个属性C={C1,C2,…,C5},其中C1表示刹车系统、C2表示防抱死系统、C3表示稳定性系统、C4表示安全气囊系统、C5表示车身薄板。3位车辆专家用D={D1,D2,D3}表示,并且这3位专家针对这5款汽车的5个属性给出了概率犹豫模糊决策矩阵。专家给出的主观属性权重均为0.2,根据专家从业经验、教育经历、社会阅历给出的专家初始权重分别为0.4、0.4和0.2。 参考文献[22-25],求解步骤如下。 步骤1对初始决策矩阵根据式(2)和定义2进行标准化处理得到标准化矩阵,如表2~表4所示。 表2 专家1给出的标准化决策矩阵Table 2 Standardized decision matrix given by expert 1 表3 专家2给出的标准化决策矩阵Table 3 Standardized decision matrix given by expert 2 表4 专家3给出的标准化决策矩阵Table 4 Standardized decision matrix given by expert 3 表5 专家整体加权决策矩阵Table 5 Overall weighted decision matrix of experts 步骤3通过式(17)~式(19),利用主客观结合的思想求得属性权重ω=(0.530 3,0.031 7,0.109 6,0.127 4,0.201 0)T。 步骤4通过坎贝拉距离公式,分别求出各备选方案与正、负理想解之间的距离后,通过式(20)和式(21)确定备选方案的收益、损失矩阵,如式(28)和式(29)所示。 步骤5利用式(10)~式(13)求出决策权重值后,再根据式(22)得到累积前景价值矩阵,如式(30)所示。 步骤6通过式(23)~式(27),利用VIKOR法进行综合排序:A1>A3>A2>A4>A5。 为了证明本文方法的可行性及有效性,将其与其他方法进行了比较,3种模型的方案比较结果如表6所示。 表6 不同方法排序结果Table 6 Sorting results of different methods 3.3.1 与文献[15]中前景理论方法比较结果分析 文献[15]的结果为A5>A4>A1>A3>A2。与本文方法所得结果不同的原因是因为文献[15]中运用了前景理论的方法,只适用于少数结果而不能应用于很多结果,且并不满足随即占优的不足。而累积前景理论方法在数学模型中能较好地兼容前景理论,更好地将多种风险态度融入模型中。实际上前景理论是累积前景理论的一个理论特例,因此,累积前景理论方法比前景理论方法更加客观、可靠;而前景理论方法更加偏主观。同时,在排序方法上,采用多准则妥协优化解法,通过主客观结合的方式进行综合排序,得到的结果更加接近现实。从表6结果看,文献[15]结果认为方案A5是最佳选择,而本文方法的结果为方案A1是最佳选择。 (28) (29) (30) 两者之间的差异,可能是由于文献[15]模型中的前景理论单纯依靠单个概率计算概率权重,比较片面,且排序方式上更加主观,导致结果较主观。例如,方案A5的特斯拉汽车,区别于其他4款传统汽车,是一款新能源汽车。所以相较于其他4个方案的传统汽车更加新颖,或许由于慕新心理,导致有些专家主观偏爱。因此本文模型更加有说服力。 3.3.2 与TOPSIS法比较结果分析 将累积前景理论与TOPSIS排序方式相结合,得到的结果为A3>A1>A2>A4>A5。本文方法与TOPSIS方法的差异只有排名前两位的A1和A3不同,说明原方法确实偏主观。在排序方法上,VIKOR方法在TOPSIS方法的基础上提出了一个具有优势率的折衷方案, 能够同时考虑群体效用最大化和个体遗憾最小化以及融入决策者主观偏好,因此具有更高的排序稳定性和可信度。得到的结果也更加接近现实,更加能够证明本文方法的可行性和适用性。 3.3.3 与前景理论+VIKOR结合法比较结果分析 将前景理论与VIKOR排序方式相结合,得到的结果为A1>A5>A4>A3>A2。本文方法与前景理论+VIKOR方法得出的最优方法结论相同,说明引用VIKOR方法能更准确地得到最优结论,在考虑群体效用最大化和个体遗憾最小化的基础上,能更好地反映决策者偏好,因此该方法得到的排序更加稳定可靠。 3.3.4 与改进的聚集算子比较结果分析 将文献[26]提出的改进的聚集算子方法用到本文算例中,得到的结果为A3>A5>A4>A1>A2。结果与本文方法差别较大,本文方法假设决策者并不完全理性,说明在决策过程中,纳入决策者心理特征是有必要且十分重要的。 (1)将累积前景理论与VIKOR相结合,既完善了决策者的心理行为,又考虑了决策者的主观偏好。 (2)摒弃传统欧式距离的距离公式,采用加权的坎贝拉距离公式,使结果更加客观。 (3)调节决策者确定客观专家权重,通过最小相对熵原理主客观结合确定综合属性权重值。 虽然在原有的方法上,本文方法进行了一定程度上的改进,使多属性决策过程更加客观;但是仍有需要深究改进之处。未来可考虑在决策过程中引入后悔理论等方法,从不同角度考量决策者的心理行为;且研究中的决策者数量较少,实例不够复杂,在实际应用中的可行性还需要进一步考量。1.2 累积前景理论
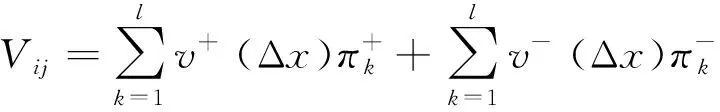
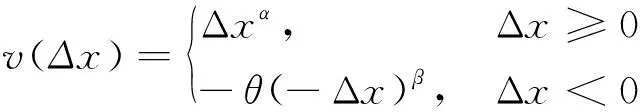

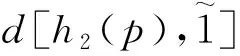
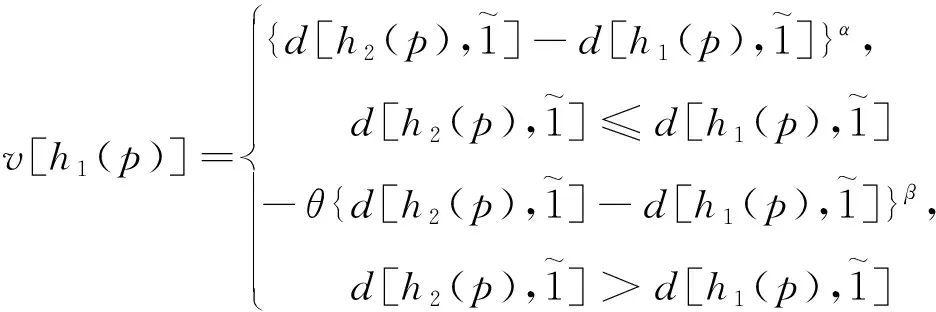


2 概率犹豫模糊多属性决策方法
2.1 多属性群决策问题描述
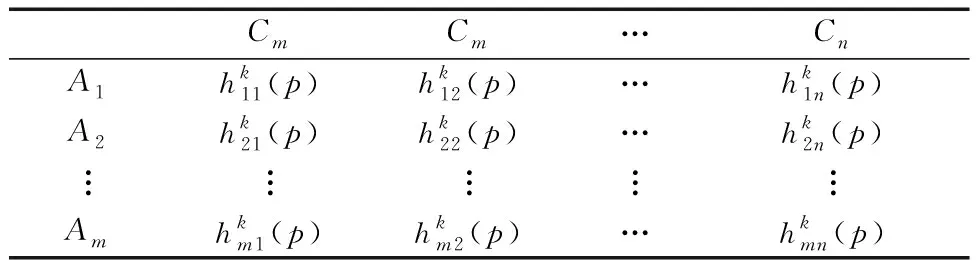
2.2 调节决策者权重系数
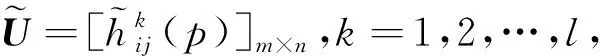
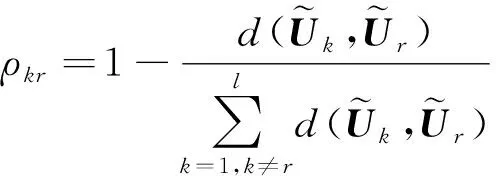
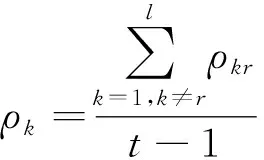

2.3 整体属性权重确定模型
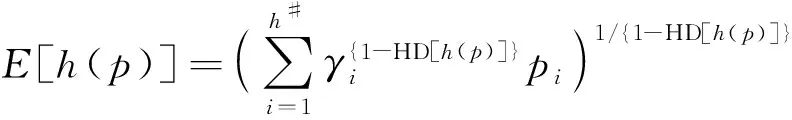
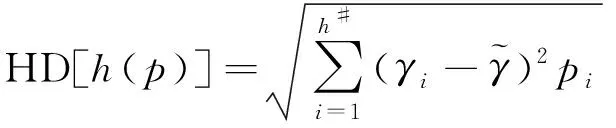
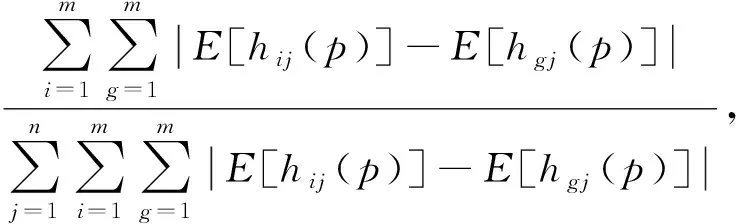
2.4 基于累积前景理论的VIKOR排序模型构建
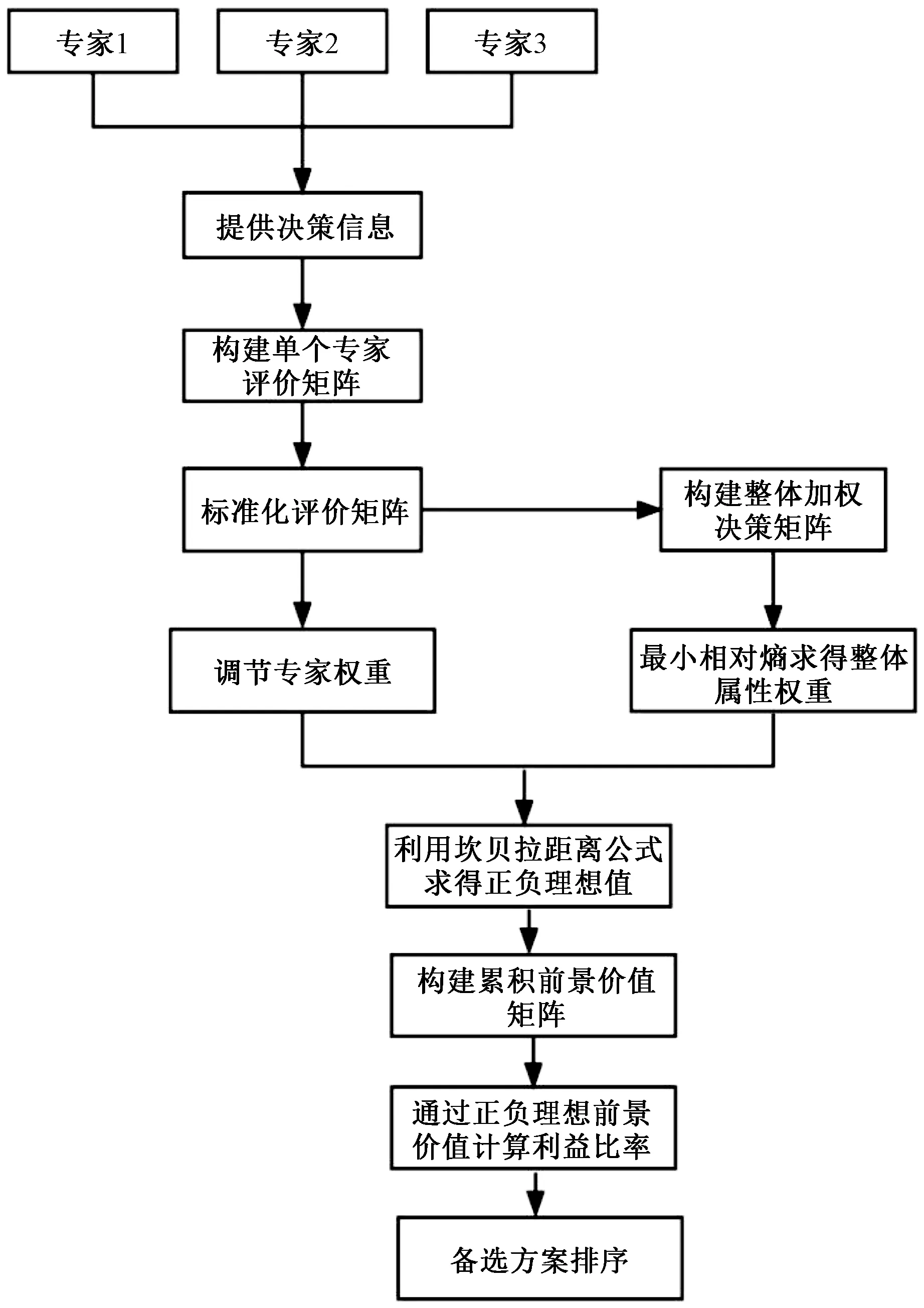
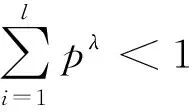

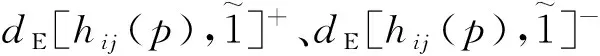

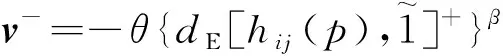
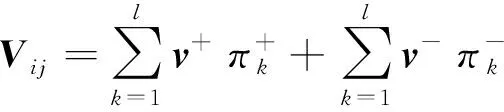
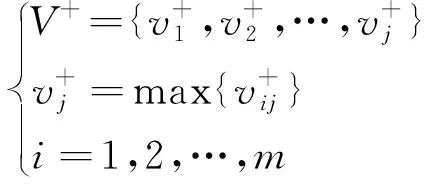


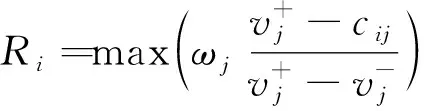
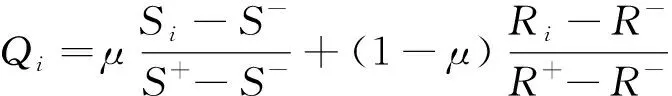
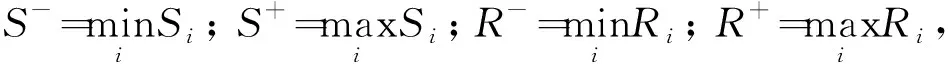
3 实例分析
3.1 问题描述
3.2 问题求解
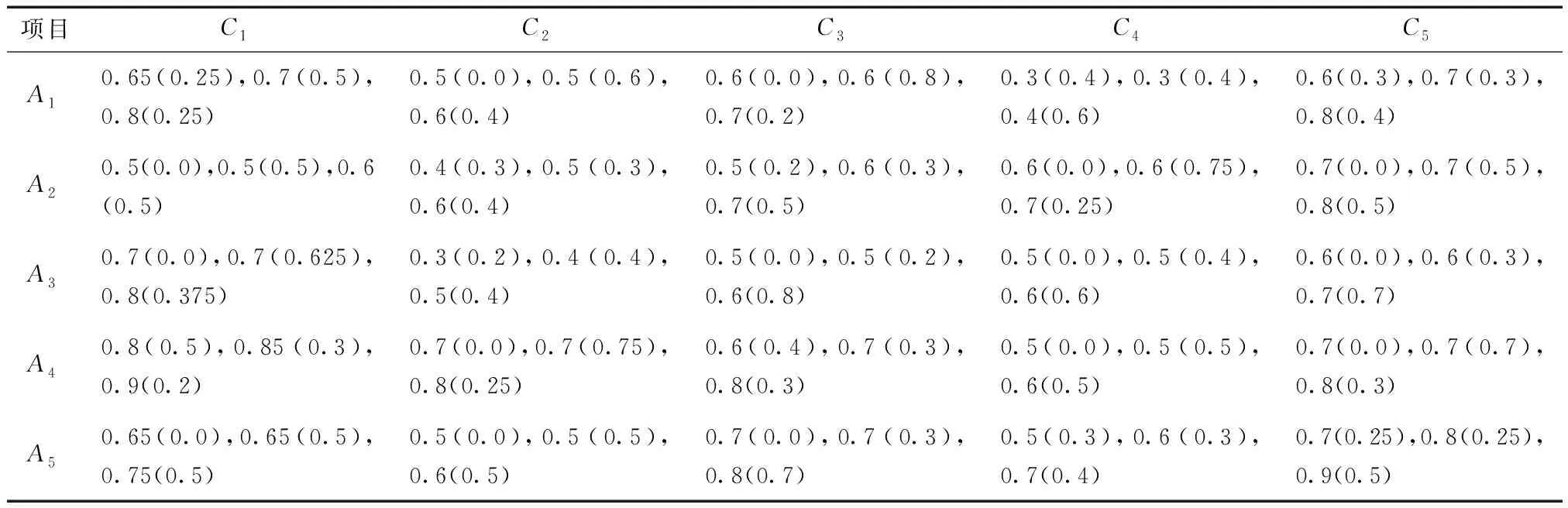
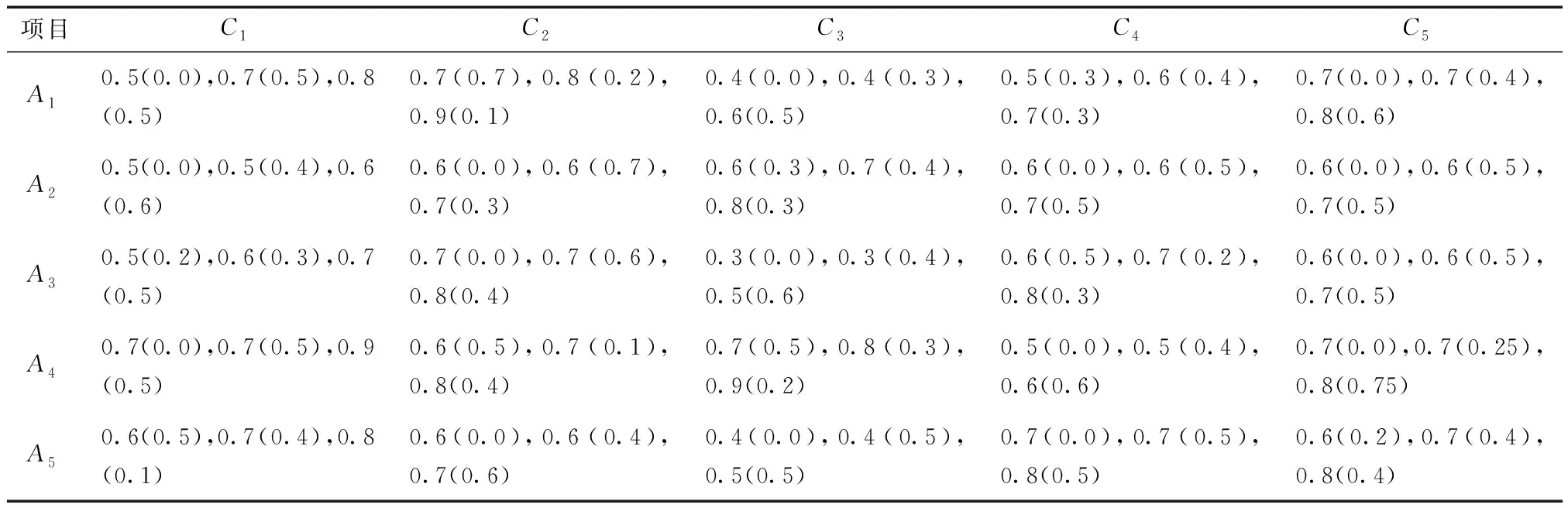

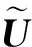
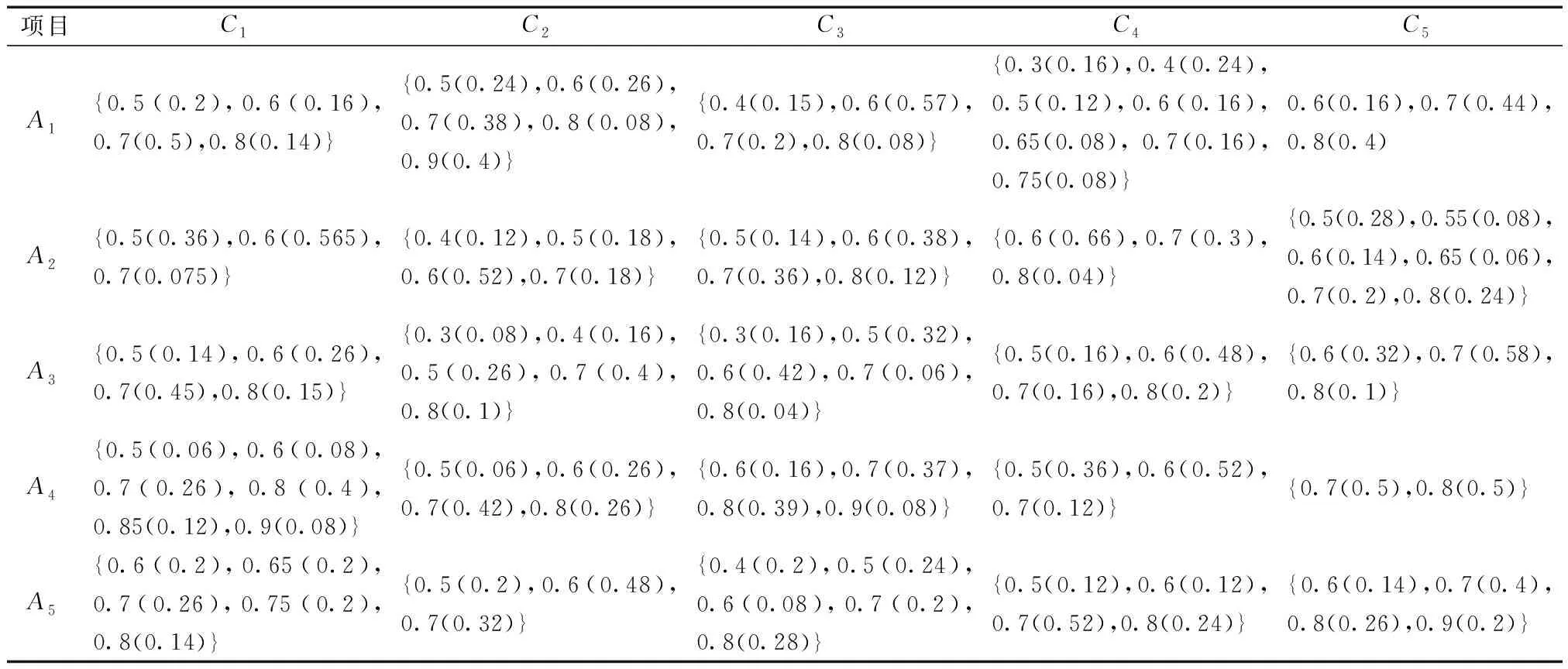
3.3 对比分析
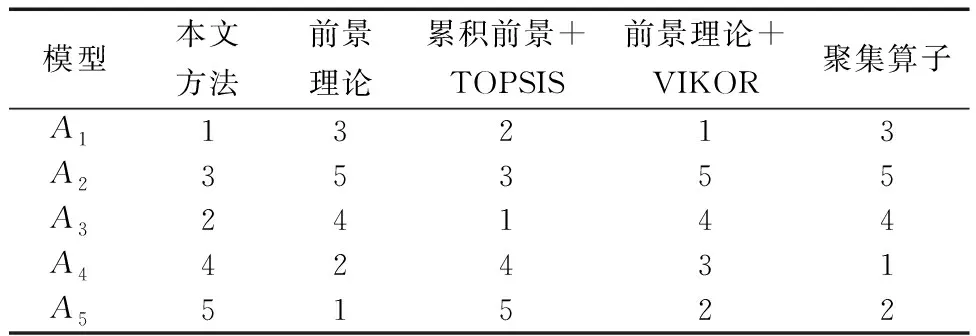


4 结论

