双混沌自同步流密码算法的设计与应用*

李 宏,张子睿,陈 平

(广东工业大学 自动化学院,广州 510006)

0 引 言

视频通信给人们带来了极大的便利,也带来了隐私泄露的重大风险。近年来,视频信息泄露等网络安全问题屡见报道,而利用密码技术进行加密防护是保护视频数据安全的有效方法。

在现有的加密算法中,AES和DES等传统分组密码算法虽然具有良好的安全性,但不适用于实时视频加密应用场景。由于视频数据传输量大,实时性强,且数据冗余度高,用于文本加密的传统分组密码难以满足视频安全及实时加密传输需求[1]。而混沌加密算法具有良好的伪随机性、初值敏感性以及较高的运算效率,具备良好的安全性能,同时还能满足视频传输的实时性需求,因此混沌流密码算法相比传统分组密码更加适用于实时视频加密应用场景中[2]。

混沌加密算法主要分为开环加密算法和闭环反馈加密算法两大类。在开环混沌加密算法中,由于密文信息不参与混沌系统的迭代运算,混沌序列的产生机制与明文信息无关,因此,密码分析者可以通过选择明文攻击、选择密文攻击等密码分析方法来获取加密算法的等效密钥。闭环反馈混沌加密算法则是将密文信息反馈到混沌系统中,混沌系统所生成的混沌序列与明文或密文相关,一旦明文信息改变,则混沌系统将产生完全不同的混沌序列,因此,密码分析者无法直接获取闭环系统的等效密钥,只能通过密码分析方法获取加密算法的原始密钥来破译密文信息,从而加大了密码破译难度。值得注意的是,在闭环反馈混沌加密算法中,有一类基于混沌反控制的自同步流密码算法[3-5],在实际应用场景如手机、ARM、FPGA多媒体混沌保密通信系统中具有重要的应用价值。

由于文献[3-5]提出的基于混沌反控制n维自同步混沌流密码算法(n-dimensional Self-synchronous Chaotic Stream Cipher Algorithm,n-D SCSCA)(n=3,7,8)具有较好的安全性能及应用价值,因此本文通过密码分析方法分析此类密码算法存在的安全漏洞,并基于n-D SCSCA的算法模型提出改进算法以提高密码算法的安全性能。n-D SCSCA算法模型的安全漏洞源于自同步功能,由于该功能将密文反馈回非线性反控制器中,因此该算法无法抵御选择密文攻击与分别征服攻击相结合的密码安全分析。

为了提升此类算法模型的安全性能,本文提出一种三维双混沌自同步流密码算法(3-dimensional Dual-chaotic Self-synchronous Stream Cipher Algorithm,3D DCSSCA),基于混沌反控制方法设计混沌系统。该算法由两个离散时间混沌系统构成,将第一个混沌系统状态变量作为第二个混沌系统的反控制器,由于反控制器保持非线性特性,且密文不参与反控制器的运算,分析者无法通过消除反控制器这个非线性项以进一步破译密钥参数,因此改进算法能够抵御选择密文攻击与分别征服攻击相结合的密码分析方法。相比n-D SCSCA算法模型,该算法不仅保持了自同步功能,也能解决存在的安全漏洞,并且具有良好的实际应用价值。

1 双混沌自同步流密码算法的设计及其安全性分析

1.1 n维自同步流密码算法的安全性分析

在进行密码算法设计之前,先具体分析文献[3-5]所提出的n-D SCSCA)(n=3,7,8)存在的安全漏洞。此类算法均属于闭环反馈混沌系统,均采用取模取整方式截取状态变量或多个状态变量乘积低八位对视频信息进行加密。通过文献[6-7]提出的选择密文攻击与分别征服攻击相结合的分析方法可以破译此类算法大部分密钥参数。n-D SCSCA(n=3,7,8)的算法结构及其对应的密码分析方法如表1所示,此类密码算法的一般表达式为

x(k+1)=f(aij,x(k),p(k))+g(σlp(k),εl)。

(1)

式中:k=0,1,2,3,…,p(k)为密文反馈变量;aij,σl,εl(i,j=1,2,…,n;l=1,2,3)为密钥参数;f(aij,x(k),p(k))表示采用密文反馈的标称系统;g(σlp(k),εl)表示一致有界的反控制器;x(k+1)=(x1(k+1),x2(k+1),…,xn(k+1))T,x(k)=(x1(k),x2(k),…,xn(k))T(n=3,7,8)表示状态变量。

解密端明文表达式的一般形式为

m(k)=s(k)⊕p(k)=

mod(⎣xi(k)…xi+j(k)/2w」,28)⊕p(k)。(2)

式中:k=0,1,2,3…;1≤i,j≤n;w≤64;⎣·」表示取整操作;⊕表示异或操作;mod(·,28)表示截取数据低八位操作;m(k)表示明文信息;s(k)表示解密序列。

表1 n-D SCSCA(n=3,7,8)的算法模型及其对应的密码分析方法

由表1可知,文献[3-5]所提出的基于混沌反控制自同步流密码算法均采用mod和sin函数作为反控制器,并将密文信息作为控制器的反馈控制变量,以实现加密端和解密端混沌方程的自同步。由于选择密文攻击允许密码分析者通过选取特定的密文信息将其反馈至控制器中,使控制器的运算结果为0,则解密端混沌方程退化为线性方程。具体是将p(k)=0代入式(1),得到退化后的线性迭代方程为

x(k+1)=f(aij,x(k))。

(3)

由式(1)和式(3)对比可知,退化后的线性方程因消除非线性项,为接下来采取分别征服攻击进行密钥参数破译提供了可行性。

由于存在自同步特性,此类算法模型对初值条件不敏感,加密端和解密端混沌方程在不同初始条件下均能实现快速同步,因此密码分析者能够任意选取对破译有利的初始条件进行攻击。上述的选择密文攻击已经选择密文为p(k)=0,则式(2)可以简化为

m(k)=mod(⎣F(k)(c,aij)」,28)。

(4)

式中:k=0,1,2,3…;F(k)(c,aij)表示初始条件和密钥参数的关系表达式;aij表示密钥参数;c表示初始条件值。

式(4)可以采取单个状态变量或者多个状态变量乘积的低八位进行加密和解密操作,根据这两种情况采取不同策略的分别征服攻击方法进行密钥参数破译。对于采用单个状态变量的情况,则选择初始条件为

{c}={x1(0),x2(0),…,xn(0)}T=

{(c1,0,…,0),(0,c2,0,…,0),…,

(0,0,…,cn-1,0),(0,0,…,0,cn)};

对于采用多个状态变量相乘的情况,则选择初始条件为

{c}={x1(0),x2(0),…,xn(0)}T=

{(c1,0,…,0),(0,c2,0,…,0),…,

(c1,c2,0,…,0),(c1,c2,c3,…,0),…,

(c1,c2,…,cn-1,0),(c1,c2,…,cn-1,cn)}。

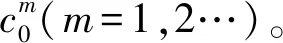
(5)

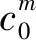
1.2 三维双混沌自同步流密码算法的设计

本文基于表1的算法模型及其安全分析结果,提出一种三维双混沌自同步流密码算法3D DCSSCA以改进加密算法的安全性能。双混沌自同步流密码算法由两个离散时间混沌反控制系统构成,其中第一个混沌系统迭代产生的状态变量作为第二个混沌系统的反控制器,第二个混沌系统生成的混沌序列则用于明文的加密操作,并将密文变量反馈至第二个混沌系统中,从而实现加密端与解密端混沌系统的自同步功能。三维双混沌自同步流密码算法3D DCSSCA具体设计流程如下:

首先,根据文献[8]的理论推导过程设计一个三维离散时间混沌系统,得第一个混沌系统f1(bij,z(k),σ,ε)的迭代方程为

(6)

式中:z(k+1)=(z1(k+1),z2(k+1),z3(k+1))T;z(k)=(z1(k),z2(k),z3(k))T(k=1,2,3…)表示状态变量;bij(i,j=1,2,3),σ,ε表示系统参数。

在设计第二个混沌系统之前,先设计一个三维渐进稳定标称系统:

(7)

利用混沌系统自身全局有界、高增益的动力特性,将式(6)迭代产生的状态变量z3(k)作为式(7)的控制器,使得渐进稳定标称系统全局有界且具有正的Lyapunov指数,从而得到第二个混沌系统f2(aij,x(k),z3(k))的表达式为

(8)

式中:z3(k)和xi(k)(i=1,2,3)分别表示控制器与混沌状态变量。由于式(6)和式(8)两个系统都是基于渐进稳定标称系统进行混沌反控制得到,因此所选择的参数必须保证标称系统为渐进稳定,据此参数具体选择如下:b11=0.09,b12=-0.37,b13=0.1,b21=-0.1,b22=-0.18,b23=-0.37,b31=0.27,b32=-0.27,b33=0.19;a11=0.205,a12=-0.595,a13=0.265,a21=-0.265,a22=-0.125,a23=0.595,a31=0.33,a32=-0.33,a33=0.47;ε=3.3×108;σ=2.5×105。由于控制器的反控制作用,式(6)和式(8)系统在全局有界条件下Lyapunov指数全部为正,因此成为混沌系统,通过仿真得到式(8)的混沌吸引子相图如图1所示。至此完成了两个混沌系统的设计。

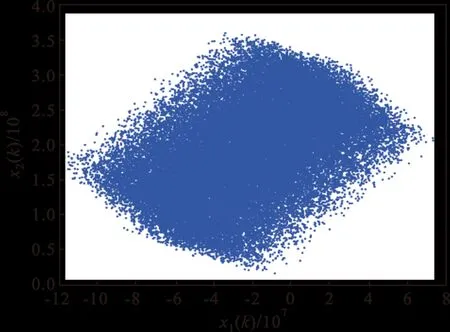
(a)x1(k)-x2(k)相图

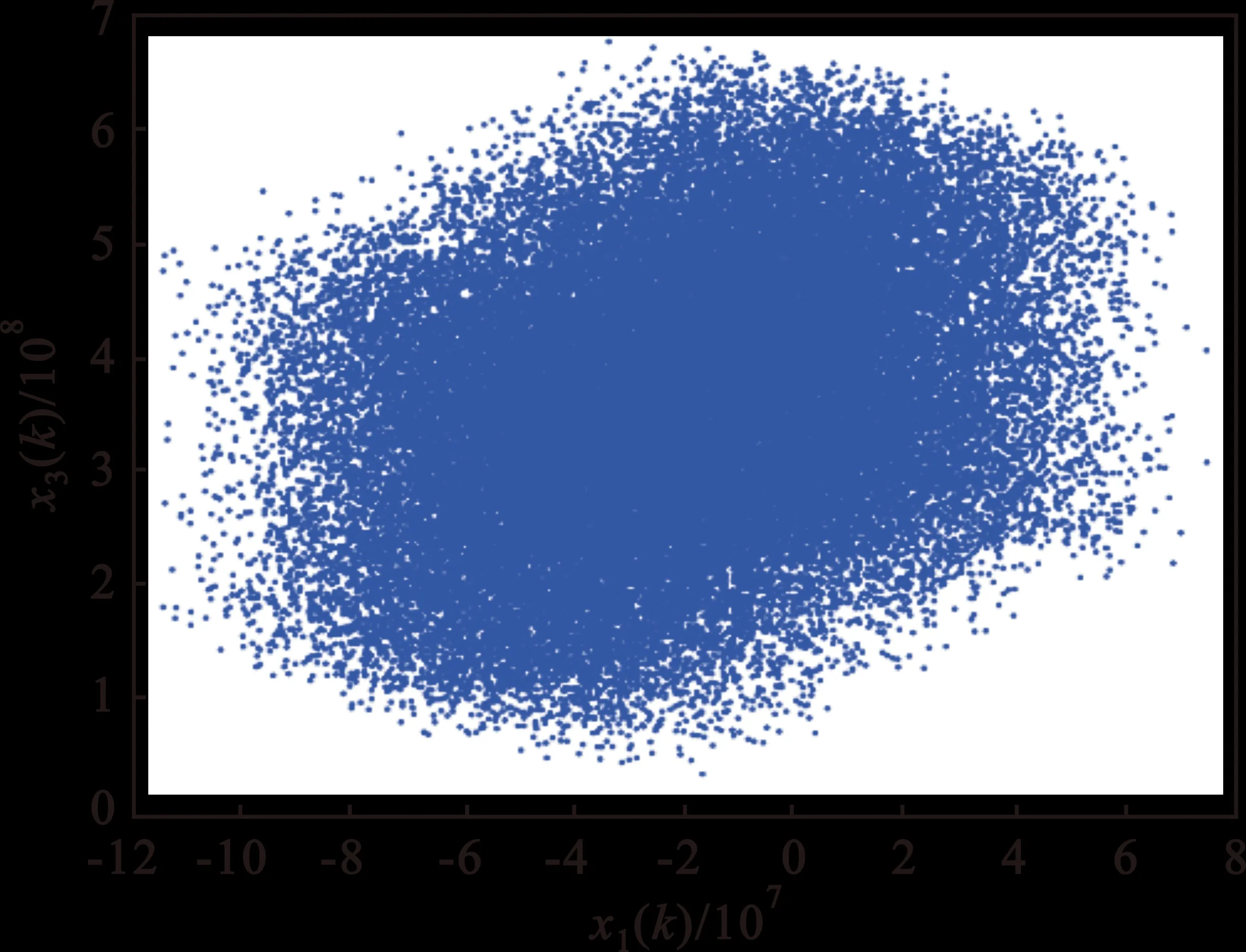
(b)x1(k)-x3(k)相图

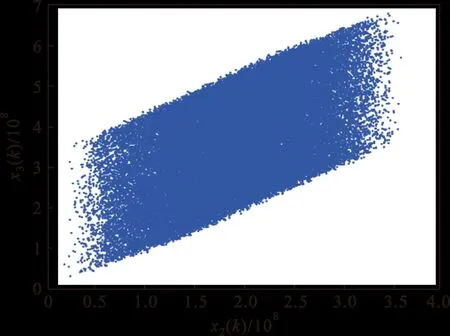
(c)x2(k)-x3(k)相图图1 混沌吸引子相图

接着,进一步设计解密端与加密端混沌方程之间的自同步功能。将密文变量p(k)反馈回式(8)中,得3D DCSSCA算法的数学表达式为

(9)

p(k)=(mod(⎣x3(k)」,28))⊕m(k)。

(10)

为了进一步证明解密端与加密端的混沌方程满足自同步功能,在加密方程与解密方程中分别设置不同的状态变量初始值并进行仿真,结果如图2所示,3条曲线Δxi(k)(i=1,2,3;k=0,1,2,3…)分别表示解密端与加密端混沌方程3个状态变量的误差。迭代次数k≈8时,Δxi(k)=0,证明经过短暂几次迭代后加密端和解密端的混沌方程实现自同步,至此完成自同步设计。

图2 自同步误差仿真结果

本文提出的3D DCSSCA算法的主要特点总结如下:

1)3D DCSSCA算法与表1的n-D SCSCA算法存在重要区别,表1的密码算法均直接采用一致有界的非线性函数作为标称系统的反控制器,而本文所设计的3D DCSSCA则采用混沌系统产生的状态变量作为反控制器。在密钥参数一致的情况下,加密端和解密端混沌方程控制器的结果保持一致,因此能够实现加密端与解密端的自同步,对实际信道具有抗干扰能力。

2)正是由于3D DCSSCA控制器与密文无关因此能够抵御密码攻击。在选择密文攻击的条件下,密码分析者无法通过选取特定的密文信息以消除控制器这一非线性项,非线性项的存在有利于抵御密码分析。尽管3D DCSSCA仅仅采用单个状态变量的低八位进行加密的方法,但却能有效抵御选择密文攻击与分别征服攻击相结合的密码分析方法。

1.3 双混沌自同步流密码算法的安全性分析

对3D DCSSCA密码算法进行安全性分析。由选择密文攻击方法可知,密码分析者可以任意选择有利于破译算法的密文信息,并得到对应的明文信息。选取密文信息p(k)=0并代入式(9),得混沌迭代方程的数学表达式为

(11)

其中k=0,1,2…。将p(k)=0代入式(10),得明文表达式为

m(k)=(mod(⎣x3(k)」,28))⊕0=

(mod(⎣a32x2(k)+a33x3(k)+z3(k)」,28))。

(12)

将k=1代入式(12)中,得到第二次解密结果为

m(1)=(mod(⎣x3(1)」,28))=

(mod(⎣a32x2(0)+a33x3(0)+z3(0)」,28))。

(13)

对于3D DCSSCA算法,遍历多个非0分量初始条件的所有可能选择方式,得初始条件xi(0)(i=1,2,3)的7种选择方式的集合为

{x1(0),x2(0),x3(0)}=

{(c1,0,0),(0,c2,0),(0,0,c3),(c1,c2,0)

(c1,0,c3),(0,c2,c3),(c1,c2,c3)}。

(14)

在选择密文攻击的情况下,根据式(14)中的7种初始条件,可以得到对应明文信息mi(1)(i=1,2,…,7)。值得注意的是,密文信息pi(1)(i=1,2,…,7)以及对应的明文信息mi(1)(i=1,2,…,7)均已知,虽然密文信息pi(1)(i=1,2,…,7)保持不变,初始条件ci(i=1,2,3)一旦改变,明文信息mi(1)(i=1,2,…,7)也会相应改变。因此,将式(14)中7种初始条件带入式(13)中,分别得到与初始条件相对应的明文信息表达式:

(15)

由式(15)可以看出,第二次解密结果mi(1)(i=1,2,3,4,5,6,7)中均包含着非线性控制器z3(0)。z3(0)在明文信息表达式中作为一个独立的加法项,不与3D DCSSCA的初始条件相乘,故密码分析者无法通过选取合适的初始条件值来获得密钥参数表达式的正确信息。同理,随着迭代次数的不断增加,mi(k)(k=2,3…)中仍含有z3(k)(k=1,2,3…)。特别地,由于z3(k)是第一个混沌系统迭代产生,故在解密过程中,mi(k)表达式中的非线性控制器z3(k)均不相同,因此能够抵御分别征服攻击。

综上可知,本文所提出的3D DCSSCA密码算法与n-D SCSCA闭环反馈自同步混沌流密码算法相比,由于采用双混沌方法进行优化改进,将第一个混沌状态变量反馈到第二个混沌系统,因此能够有效抵御选择密文攻击与分别征服攻击相结合的密码分析方法,安全性能得到改善,且计算量约减少至1/3,因此能够提高加密效率。

2 实时视频混沌加密监控系统的应用

2.1 系统设计方案

基于3D DCSSCA算法的实时视频加密监控系统的设计方案如图3所示。

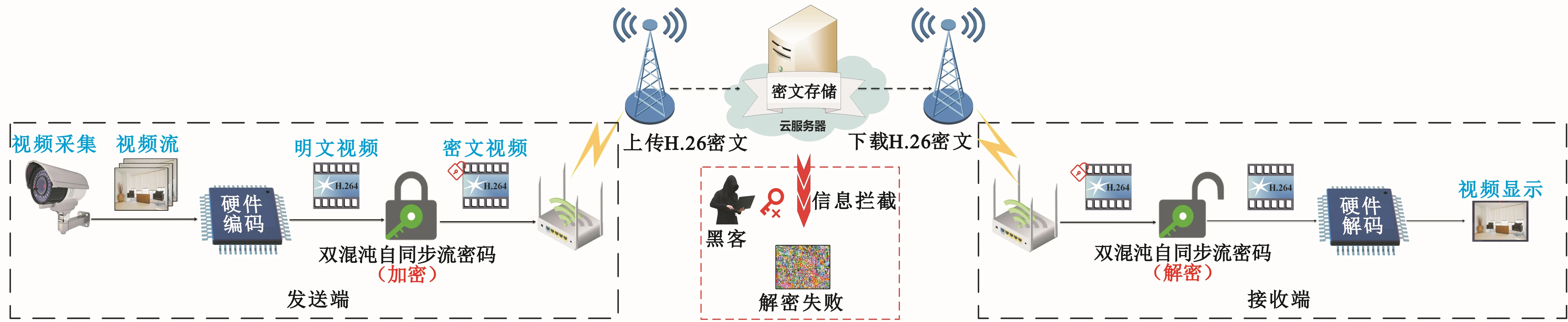
图3 实时混沌加密监控系统总原理

系统分别采用两块四核ARM Cortex A9开发板作为视频监控系统的发送端和接收端:在发送端,ARM实现视频采集、视频转码、视频预览、H.264视频硬件编码、混沌加密、TCP/IP网络发送;在接收端,ARM实现TCP/IP网络接收、混沌解密、H.264视频硬件解码、视频转码、视频显示。系统分别采用两块四核ARM Cortex A9开发板作为视频监控系统的发送端和接收端:在发送端,ARM实现视频采集、视频转码、视频预览、H.264视频硬件编码、混沌加密、TCP/IP网络发送;在接收端,ARM实现TCP/IP网络接收、混沌解密、H.264视频硬件解码、视频转码、视频显示。ARM实现视频采集、视频转码、视频预览、H.264视频硬件编码、混沌加密、TCP/IP网络发送;在接收端,ARM实现TCP/IP网络接收、混沌解密、H.264视频硬件解码、视频转码、视频显示,其中混沌加密与解密采用本文设计的3D DCSSCA密码算法,对H.264码流进行实时加密与解密。为了提升系统传输帧率,采用多核多线程技术提升系统的处理速度。为了减少加密数据量并且保持加密数据格式可识别,系统只加密H.264载荷部分,不加密头格式部分。在安全方面,假如盗窃者能够完整获取密文信息,仍然无法通过选择密文攻击以及分别征服攻击进行破译。在应用方面,尽管实际信道存在干扰信号,接收端仍然可以通过自同步功能正确解密视频数据。

2.2 混沌加密与解密方案设计方法

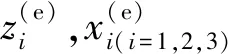
图4 混沌加密与解密设计原理

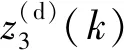
2.3 多核多线程技术

本文提出的3D DCSSCA密码算法相比表1的7维和8维密码算法,减少至约1/3的乘法运算量,体现出良好的加密效率。图3监控视频实际应用场景要求系统的传输帧率至少为25 frame/s,系统完成一帧视频加密所需的操作及耗时主要包括视频采集tcp、视频编码tec、视频加密tenc、视频传输ts,经测试得到操作总耗时T=tcp+tec+tenc+ts≫40 ms,因此单线程处理方式无法满足25 frame/s的实时性指标。为了提高系统帧率采用多核多线程技术,其原理是系统功能拆分为多个线程,每个线程耗时为ti(i=1,2…),线程耗时满足ti≤40 ms,则系统能够满足帧率要求。因此,通过多核多线程,结合3D DCSSCA密码算法高效的加密效率,系统能够取得良好的实时性能。

3 实验结果与分析

根据3D DCSSCA密码算法原理,对图3系统方案及图4的加密与解密原理进行系统的硬件实现,系统实物如图5所示。左边的ARM开发板为发送端,主要完成视频采集、编码、加密、显示与发送功能;右边的ARM开发板为接收端,主要完成视频接收、解密、解码与显示,并通过WiFi设置连路由器并形成以太网,配置双方IP地址为192.168.1.108和192.168.1.109,发送端与接收端配置完密钥参数之后可进行实时保密通信。

3.1 硬件实验结果

在上述硬件平台上进行3D DCSSCA加密算法的视频保密通信测试,分别测试密钥匹配情况下和密钥失配情况下的实验效果。在视频分辨率为1 280 pixel×720 pixel的情况下,发送端原始视频采集与显示的实验结果如图6(a)所示;在密钥匹配的情况下,即

σ(e)=σ(d)=σ,ε(e)=ε(d)=ε,

接收端正确解密与解码的实验结果如图6(b)所示;在密钥失配的情况下即上述密钥之间存在至少一个参数不相等时,接收端解密失败的实验结果如图6(c)所示。

图6 基于双混沌自同步流密码算法的实时视频混沌加密监控系统实验结果

由实验结果可知,当密钥匹配时,接收端能够正确解密视频并且实时显示;当密钥失配时,接收端解密失败,视频解码错误无法显示正确视频图像。因此,该系统成功实现了视频加密监控功能。另外,经测试,在视频分辨率为1 280 pixel×720 pixel的条件下,系统平均视频传输帧率高达30 frame/s,满足实时视频传输的帧率技术指标。

3.2 安全性分析

3.2.1 TESTU01测试

现有低维混沌系统的统计特性可能可以通过NIST或Diehard测试,其具体原因是在迭代次数少的情况下并未暴露混沌退化现象。相比NIST和Diehard测试,TESTU01是更为严格的统计特性测试,即使混沌系统能够通过TESTU01测试中的初级测试套Small Crush测试与中级测试套件Crush,也很难通过样本数据量高达10 Tb的高级测试套件Big Crush。

3D DCSSCA的TESTU01测试结果如表2所示,其10 Tb的测试数据样本通过截取混沌变量低8位s(k)=mod(⎣x3(k)」,28)的方式产生。由测试结果可知,本文所提出的三维混沌加密系统能够顺利通过TESTU01测试,证明3D DCSSCA加密序列具有良好的统计特性。

表2 TESTU01测试结果

3.2.2 密钥参数敏感度测试

当混沌系统的密钥参数失配误差很小且加密信息无法正确解密时,表示密钥参数对失配误差非常敏感;若失配误差值越小,则混沌系统的密钥敏感度越好。

Δa11∝10-8Δa12∝10-8Δa13∝10-9Δa21∝10-8Δa22∝10-8Δa23∝10-9Δa31∝10-2Δa32∝10-8Δa33∝10-9Δb21∝10-18Δb22∝10-17Δb23∝10-18Δb31∝10-18Δb32∝10-17Δb33∝10-18Δx1(0)∝10-18Δx2(0)∝10-13Δx3(0)∝10-12

根据图7,可得破译各个密钥参数的攻击复杂度为

O(Deducingaij,bij,xi(0))=

O(10243)≫2128。

(16)

由式(16)的计算结果可知,3D DCSSCA能够有效抵御穷举攻击。

4 结束语

针对n-D SCSCA算法模型存在安全漏洞的问题,本文提出了改进算法3D DCSSCA,能够有效抵御选择密文攻击与分别征服攻击相结合的破译方法,提高了n-D SCSCA算法模型的安全性能。由于3D DCSSCA算法方程计算量相对较少,在多核多线程技术优化下,系统帧率可到每秒25帧以上,体现出良好的安全性能和加密效率。未来的研究工作是将密码算法进一步应用到视频监控系统场景之中,解决高分辨率视频保密通信安全性能、格式兼容性及实时性问题。