永磁转子表磁检测偏心修正系统开发
王 明,荣佑民,黄 禹,张 勇,曾真寅
(1.华中科技大学机械科学与工程学院,武汉 430074;2.广东机电职业技术学院先进制造技术学院,广州 510000;3.麦格雷博(深圳)电子有限公司,深圳 518000)
0 引言
近年来随着稀土永磁产业飞速发展,永磁体已广泛应用于医疗[1]、交通[2]、仪器仪表[3]等众多领域,学者们对永磁体的性能也愈加关注。表磁(永磁体的表面磁感应强度)是永磁体性能的重要指标之一[4],表磁测量的精准性直接影响着产品的质量。
目前,永磁转子磁感应强度分布的主要分析手段:有限元分析[5]、数值解析[6]及实验测量。有限元分析用于求解静态、动态磁场问题,通过灵活设置边界条件及材料性质,能够仿真计算出不同材料和结构形式的永磁体理想磁感应强度;数值解析的基础理论一般为,基于安培分子环流定律的等效电流模型以及基于库伦定律的等效磁荷模型。有限元分析和数值解析大多不单独使用而是配合实验,对构建出的转子模型进行理论验证[7];实验测量则是基于霍尔效应用高斯计对磁极的表面磁场进行直接测量,适用于实际产线上快速检测产品性能。HIROSE等[8]利用霍尔器件对回旋加速器中的大型永磁体进行磁场的精确测量,王晓明等[9]则基于LabWindows/CVI软件及B&H测试仪研制了一套可实时显示、查询永磁体磁场分布系统。
在实验测量永磁转子过程中,由于转子表面是坚硬的硅钢片,为了减少检测探头的磨损,探头不会直接接触转子表面。而转子在安装的过程中存在着随机偏差,这就导致在转动检测时会出现偏心现象。因为磁感应强度与检测距离之间有很强的相关性[10],偏心现象会严重影响磁场数据采集的准确性。针对这种现象,目前普遍存在两种方法,一是使用可变性柔性探头[11]紧贴磁体表面测量,但转子表面并不光滑,在转动过程中会出现滑动摩擦,难免会损伤探头和转子;二是使用高精密的机械设备,但这样会极大地增加成本。
本文针对测量永磁体转子表面磁场分布时存在的偏心现象,基于安培分子环流模型,利用毕奥-萨伐尔定理开发了一种表磁偏心修正的系统。该系统仅需在测量前建立校准数据库,便可极大地保证对永磁转子表磁的精确测量。
1 磁场分布的数学描述
1.1 永磁转子的基本结构
永磁转子的组成部分一般可分为转子铁芯以及永磁磁极。相较于传统的电励磁电机由绕组产生磁场,永磁转子则是由永磁体产生磁场。而根据永磁体放置的位置以及方式的不同,可分为以下3类:插入式、内置式和表贴式[12]。插入式转子充分利用了转子磁路不对称所产生的磁阻转矩,提高电机的功率密度,但其漏磁系数和制造成本较高,因此多用于传动永磁电机。内置式[13]转子具有较强的抗退磁能力,同时它还有峰值转矩大、功率密度高、恒功率运行范围宽等特点;但由于其成本高、永磁体漏磁相对较大,故多用于中高速永磁同步电机。表贴式转子结构较为简单,磁链谐波分量较少,更容易产生正弦波磁动势,响应速度快,但同时它调速范围较小、功率密度低,抗退磁能力较差,并且没有磁阻转矩,所以适合用于伺服驱动。
1.2 永磁转子空间磁场分析
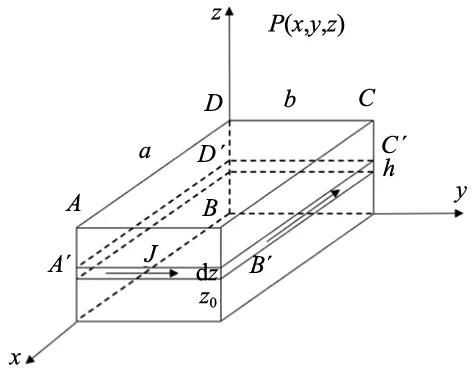
在研究转子空间磁场分布时,可以将转子磁极上的永磁体等效成理想的矩形永磁体。现有一块尺寸为a、b、h(如图2)的矩形永磁体沿一个方向均匀充分充磁化且达到饱和状态,此时磁体内部磁化矢量可视为一个常矢量。根据安培分子环流假设可知,外部空间任意一点的磁场均由永磁体内部所有的分子电流激发的磁场叠加形成。而由于磁体是均匀磁化,磁体内的分子电流相互抵消,所以空间中任意一点的磁场仅由永磁体表面闭合的电流环路产生。
假设磁体面电流密度为J,在永磁体外部空间中的任意一点P(x,y,z)处,由面z0和z0+dz0构成的薄层电流环产生的磁场为dB。则总磁场为:

(1)
式中:Bx,By,Bz分别为薄层电流环A′B′C′D′在P点产生磁场的x、y、z方向分量。可以将该电流环分为4段,下面以A′B′为例。
由毕奥-萨伐尔定律得:
(2)
式中:μ0=4π×10-7H/m为真空磁导率,r为从源点(即电流元所在位置)指向点P的矢径。于是有:
(3)
dBy1=0
(4)
(5)
式中:G=(x-a)2+(y-y0)2+(z-z0)2。

(6)
式中:Ei是以ε1,ε2,ε3为自变量的函数,且(i=1,2,3),于是可推导出4段电流叠加产生的磁场:

(7)
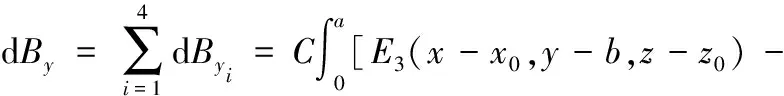
(8)
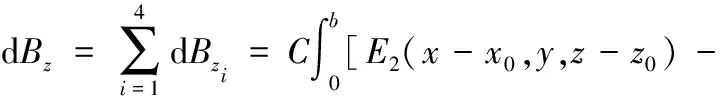
(9)
将式(7)~式(9)代入式(1),于是空间内任一点(x,y,z)的总磁场为:
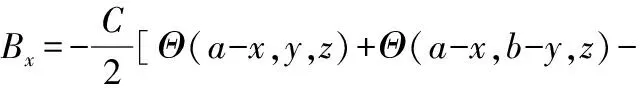
(10)

(11)
Bz=-C[W(b-y,a-x,z)+W(x,b-y,z)+
W(b-y,x,z)+W(x,y,z)+W(a-x,y,z)+
W(y,x,z)+W(y,a-x,z)+W(a-x,b-y,z)]
(12)
式中:辅助函数Θ、W的表达式分别为:
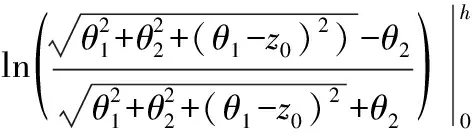
(13)

(14)

2 偏心修正模型
实际检测中主要对转子径向磁场进行测量,而由上述分析可知,饱和充磁的矩形永磁体磁场是有关空间位置、磁体尺寸、面磁化电流密度的函数,并与面磁化电流密度呈线性相关。通过坐标变换及磁场叠加可以得出,多块永磁体的磁场分布具有类似的规律。现假设有一个永磁体,已知其在位置(x0,y0,z0)的磁感应强度B0,在位置(x0,y0,z1)的磁感应强度为B1;另一个具有相同尺寸结构的永磁体在位置(x0,y0,z1)的磁感应强度为B2,则其在位置(x0,y0,z0)的磁感应强度应为B3:
(15)
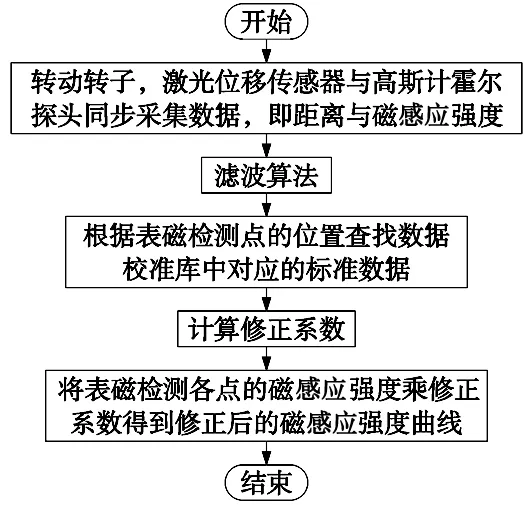
永磁转子中各个磁极的永磁体具有相同的尺寸参数,基于此可以设计出如图3、图4用于检测偏心识别及修正的方法。总体可分为两个大步骤,即校准数据库的预生成,以及实际校正过程中校准系数的计算。
2.1 基于三次样条的双向插值
在进行校准数据库生成时,为准确反映永磁转子任意位置的磁感应强度信息,需要对实验采样得到的数据进行处理。插值法不仅可以填充现有的数据,而且还可以对现有的数据进行平滑处理[14],很好地满足了实际需求。
常见的插值方法有线性插值、最近邻插值、三次样条插值等。其中线性插值仅适合较为简单的规律,不能保证在插值点的导数连续性,这就导致其插值得到的数据光滑性较差;最近邻插值未考虑周围点的影响,会产生明显的锯齿现象;三次样条由于其性质:曲线在衔接点处光滑;样条的一阶导数和二阶导数连续,因此通过样条插值可以得到一个收敛性好、光滑性好的曲面[15],同时样条插值还可以利用较低阶的多项式来实现较小的插值误差,这样便避免使用高阶多项式出现的“龙格现象”。
2.1.1 三次样条插值函数的定义
设区间[a,b]上给定一个分割:
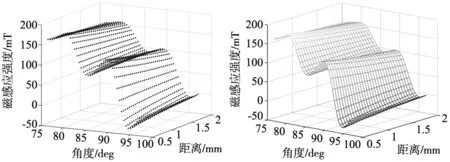
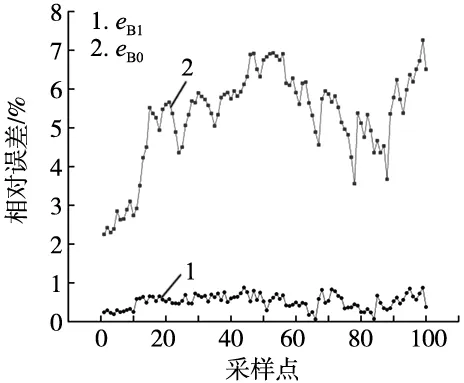
Δ:a=x0 S(x)为[a,b]上的函数,且满足下列条件: (1)S(x),S′(x),S′′(x)在区间[a,b]上连续; (2)S(x)在每个子区间[xi,xi+1]上是三次多项式(i=0,1,2,…,n-1); 则称S(x)为关于分割Δ的一个三次样条函数。 如果再给定函数f(x)在分割Δ的节点上的函数值fi=f(xi),(i=0,1,2,…,n)且满足条件: (3)S(xi)=f(xi),i=0,1,2,…,n,即经过所给的每个节点。 那么就称S(x)为函数f(x)在[a,b]上关于分割Δ的三次样条插值函数。 2.1.2 三次样条曲线的构造与求解 关于样条插值函数的求解学者们已做大量研究[16],这里只做简单介绍,不进行具体推导。本文考虑使用三弯矩法对三次样条插值函数进行求解[17]。S(x)在子区间[xi,xi+1]上是三次多项式,可令: Mi=S′′(xi),Mi+1=S′′(xi),hi=xx+1-xi 于是有: (16) (17) (18) 利用样条插值函数的性质(3)及其一阶导连续可得下列方程: μiMi-1+2Mi+λiMi+1=Ti (19) (20) 式中: 。 通过求解上述方程组,可以求得Mi(i=0,1,2,…,n),代入S(x)即可以求得每个子区间[xi,xi+1](i=0,1,2,…,n-1)上的三次样条插值函数。 如图3所示流程,根据标准永磁转子的磁场数据进行校准数据库生成。首先,绘制标准转子的磁场曲线,如图5所示。磁场曲线具有标准的对称性,因此只需将其中半个磁极的数据作为采集点,本次设定的采集点间距为0.5°。 对于每个采集点,收集其磁感应强度-距离信息。在实际表磁检测中,一般设定探头的检测距离为1~1.5 mm左右,而由偏心产生的误差在±0.5 mm以内,因此本次磁感应强度-距离表格中距离的设定范围为0.5~2 mm,采集间隔为0.05 mm。图6为其中一个采集点的磁感应强度-距离曲线。 圆周方向编码器分辨率为36 000脉冲,径向方向激光位移传感的精度为0.01 mm,基于此进行双向三次样条插值。首先对圆周方向的磁感应强度进行插值,得到在检测距离确定时转子在任意位置的磁感应强度,图7a为圆周方向插值前后磁感应强度与真实值的对比图;然后进行径向插值,得到转子上任意点在不同距离上的磁感应强度,图7b为径向插值前后磁感应强度与真实值的对比图。双向插值后的数据可合成磁感应强度曲面,即数据校准库。最终磁感应强度曲面效果如图8所示。从图7和图8的比对中可以看出,进行双向三次样条插值后,磁场曲面更加光滑,各个位置的磁感应强度的与真实值更加贴近。 表磁检测系统主要由两坐标运动平台,旋转平台、检测单元、电控柜、HMI触摸屏及上位机组成,如图9所示。两坐标运动平台采用光栅尺作为位移传感器,精准控制位移距离;旋转平台使用套筒治具对转子进行轴心定位,并在检测中配合编码器对转子在不同角度的磁场数据进行采集;检测单元由高斯计(SHENZHEN MAGNET LAB的TM-10A型数字式)以及激光传感器(PanasonicHG-C1030)构成;HMI触摸屏和上位机作为检测过程中参数的人机交互界面,实时展示并计算磁场数据,并与高斯计和PLC进行通讯;同时工作台上还嵌有启动、急停等按钮。 试验人机交互下偏心检测修正系统的修正误差,探究该方法的准确性,以及在实际表磁检测中的适用性。 选取一个待检测的永磁转子,随机初始一个轴心位置偏差,设定探头检测距离为1.00 mm。选取并测量100个采样点的磁场数据,并根据校准数据库计算修正系数进行逐点校正。 修正误差的计算公式可表述为式(21)和式(22): (21) (22) 式中:i=1,2,3,…,100,Bti表示第i个采样点在当前距离测得的磁感应强度,Bmi表示该采样点经修正过后的磁感应强度,Bri表示该采样点在设定距离处实际测得的磁感应强度。 图10为修正前后采样点磁感应强度相对偏差的对比图。经过偏心修正后,采样点的磁感应强度相对偏差可控制在0.9%以内。这里仍然存在着误差的原因有以下几个方面: (a) 插入式 (b) 内置式 (c) 表贴式 图2 矩形永磁体磁场解析计算示意图 图3 校准数据库生成图 图4 实际表磁检测的校准 图5 标准转子磁场数据曲线 图6 磁感应强度-距离曲线 (a) 磁感应强度随角度变化曲线 (b) 磁感应强度随距离变化曲线 (a) 散点图 (b) 插值前的磁场曲面 图9 表磁检测实验平台 图10 相对误差对比图 (1)硬件方面,检测探头即高斯计与激光位移传感器本身存在着最小分辨率; (2)真实转子的磁场分布与理论分析会有些许出入,比如转子充磁未完全充分均匀、外界干扰等。 实验表明,该修正方法针对现有的偏心现象有明显的效果,0.9%的相对误差已完全满足了对永磁转子表面磁场的检测要求。 本文针对在使用高斯计直接对永磁转子表面磁场分布进行测量时出现的偏心问题,基于分子环流模型,利用毕奥-萨伐尔定理分析了转子磁极的空间磁场分布,开发了一种用于表磁偏心修正的系统。该系统首先通过对采样点的磁感应强度收集,建立校准数据库;并对离散采样点的数据进行基于三次样条函数的双向插值,对数据库进行扩充;然后在实际检测中通过计算各测量点的修正系数对其进行逐点修正。 最终得出以下结论:①使用分子环流模型分析永磁转子空间磁场分布具有较强的适用性;并根据推得的磁场表达式可知,磁体的径向磁感应强度与采样点的距离及位置相关,且与面磁化电流密度呈线性相关;②三次样条双向插值在原有数据进行扩充,可使得到的磁场分布曲面更加光滑并与实际值更加贴近;③经该系统修正后的磁场数据与真实值的相对误差可控制在0.9%以内,该修正系统是可行的且精准度较高。

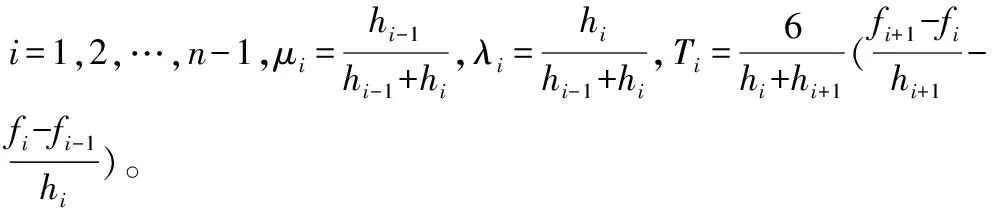


2.2 磁场曲面双向插值
3 表磁检测偏心修正实验
3.1 检测系统组成
3.2 偏心检测的修正误差





4 结论

