基于改进遗传算法的多线性缓冲区联合调度*

王子若,刘明周,王小巧

(合肥工业大学机械工程学院,合肥 230009)

0 引言

路由调度问题是定制化生产模式下需要解决的难点问题之一,其直接影响着生产运营效率。多品种小批量的定制化生产模式下,依赖于人员经验进行生产过程的调度与管理难以进行成本的控制。例如,对于汽车整车生产制造商,路由调度策略是指在制品经过缓冲区域存放位置的路由方案集合,在定制化生产模式下汽车涂装作业采用混合型产品生产线[1],日均产车量500左右,但换漆次数高达70%左右,造成涂装作业在油漆、时间、成本等方面的资源浪费,成为汽车生产的瓶颈工艺之一。因此,亟需解决定制化生产模式下的汽车生产过程中在制品的路由调度最优化问题。

路由调度主要用于解决复杂场景下车辆路径规划[2-5]及重排序调度[6-8]等问题,其方法主要包含整数规划、启发式规则、智能优化算法等。整数规划方法是基于约束和目标建立精准的数学模型[2-5],但该问题经证明为NP-Hard问题[9],无法精确求解。启发式规则方法主要是建立车辆入库及出库规则约束实现车辆路由排序[6],但因其仅基于规则调度,对不确定的生产过程适应性差。智能优化算法是一种适合并行处理的具有全局优化性能和通用性强的算法[10],包含解决静态问题的启发式算法,如遗传算法[11]、蚁群算法[12]、改进启发式方法[13],以及解决动态问题的强化学习算法,如Q-学习[14]、DQN算法[15-16]、Actor-Critic[17]等,但因其训练复杂、实际生产动态因素较多、无法保证有效性等原因,实际生产中应用效果不佳。

但因涂装车间具有多线性缓冲区域的生产工艺布局,在涂装车间实际生产节拍45JPH下需要更高效的方法,以此来适应生产节拍的需求。因此,根据涂装车间内生产工艺布局及上下游生产需求,以多线性缓冲区为切入点,综合考虑涂装作业处颜色切换问题和总装车间生产需求,以喷涂工位处颜色切换次数最少和总装生产需求队列偏差最小为目标,输入待喷涂车辆集合,建立多影响因素及多目标MILP模型,入库操作基于启发式规则进行路由推荐,出库操作通过改进遗传算法求解,输出涂装车间喷涂作业前多缓冲区域的车辆路由调度方案及涂装喷涂作业车辆序列,解决了定制化生产模式下的车辆调度问题,减少生产过程的管理复杂度和降低整体的生产成本。并在此基础上,提出一种新的改进遗传算法进行路由调度策略的优化,通过不同实例验证了方法的有效性和可行性。

1 多存储区联合路由调度模型

1.1 问题分析

1.1.1 生产流程及布局分析

汽车制造厂商为满足市场多样化需求,其四大核心工艺均采用混合型产品生产模式,车辆生产物流顺序为冲压-焊装-涂装-总装,而信息流根据订单需求逆推,造成实际生产下线顺序与目标作业顺序之间总具有差距,且在涂装喷漆作业处面临频繁换漆问题,为解决现存难点问题,汽车制造厂商设置多个线性缓冲区域进行车辆重排序调整车辆队列,线性缓冲区域由多条平行的车道组成,每条车道设置多个车位,遵循先进先出规则。通过多个线性缓冲存储区多次进行车辆重排,最大限度满足目标需求,实现车辆路由控制。

1.1.2 优化目标分析

通过分析涂装作业及上下游生产需求,以颜色切换次数和后续生产需求序列偏差最小为优化目标。

(1)颜色切换次数。由于客户个性化需求,车辆颜色种类设置多样,多于喷涂工位处喷头数量,当出现两个连续的车辆需面漆颜色不一致时,则定义为发生了一次颜色切换,产生以下影响:①换漆时残留在喷枪管道内的油漆以及挥发在空气中油漆分子,产生大量油漆浪费;②清洗过程产生大量存在较大污染的废水,因此车间旁建造废水处理站;③颜色切换耗费时间,妨碍生产节拍;④换漆时空气中油漆分子消杀不彻底,产生油漆污染,降低质量合格率。因此,将颜色切换次数作为车辆重排序的度量指标之一。

以0-1变量θi,r代表喷涂作业第r顺序车辆i是否需要进行颜色切换,需要切换为1,不需要切换时为0,如式(1)所示。

(1)

涂装序列集合总颜色切换次数如式(2)所示。

(2)

(2)生产需求序列偏差。生产完成的车辆需要按照后续生产需求序列进入下一车间,一般在车间之间设置缓冲区用于车辆重排序,但由于车间内部空间布局限制,车辆重排序具有较大难度。为缓解这一难点问题,将后续生产需求序列作为调度排序的目标生产序列,将生产下线与后续生产需求队列对比,若车辆提前不计入序列偏差,将车辆延迟的实际顺序与计划顺序差值记为该车辆的偏差值,如表1所示。

以变量λi代表喷涂作业集第i个任务与后续生产需求序列是否存在偏差,如式(3)所示。生产需求序列偏差计算如式(4)所示。

(3)

(4)

1.2 数学模型

1.2.1 问题描述

通过汽车生产流程分析,本研究将车辆经过多个线性缓冲区联合调度操作划分为多个过程,可近似归纳为3个工序:工序1仅包含入库操作,由待排序队列进入缓冲区域;工序2是先进行出库、再执行入库操作,由缓冲区域进入缓冲区域;工序3仅包含出库操作,由缓冲区域进入输出队列。

待排列车辆集合已知为C,工序类型1依次选择集合中车辆进入缓冲区,直至集合C车辆全部离开,可得车辆路由策略B1。工序2是将前序产生的车辆路由策略B1为已知输入,依次选择待排列车辆进入下一缓冲区,可得车辆路由策略B2。工序3是将前序产生的车辆路由策略B2为已知输入,依次选择其中车辆按照顺序进入喷涂工位,形成涂作业车辆队列集合。将下游生产需求队列与喷涂作业车辆队列集合Q计算绝对序列偏差,并计算颜色切换次数,选择最优路由策略Bi。

综上所述,汽车涂装车间多存储区联合车辆路由调度问题可归结为:待排列车辆经过多个缓冲存储区进行路由调度,已知缓冲区域的生产布局、总装生产需求队列U、待排列车辆集合C,以颜色切换次数最少及生产需求队列偏差最小为目标,输出每个缓冲区域内路由策略Bi及喷涂作业车辆队列集合Q。

1.2.2 符号说明

针对本模型所涉及到的符号,为便于理解,变量符号定义说明如表2所示。

表2 变量符号说明

1.2.3 模型假设

通过分析涂装车间生产作业流程及工艺布局实际情况,为确保模型实现,对该问题做出以下假设:

(1)假设1:以固定时长内涂装生产计划进行一次调度,待排列车辆队列集合C为已知,总装生产需求队列集合U为已知,缓冲区域布局固定且已知。

(2)假设2:涂装喷涂工位为单机器作业,同一时刻仅可工作一台车辆的颜色喷涂。

(3)假设3:涂装车间内所有缓冲区域均为线性缓冲区。

(4)假设4:针对路由调度过程,假设喷涂工位处夹具可作用于所有车型,忽略夹具更换时长。忽略喷涂工位针对不同颜色车辆、不同车型面漆的时长差异。

1.2.4 建模

通过问题分析可分别针对不同工序建立数学模型,因3个工序模型类似,下面就工序1的数学模型进行详细描述。根据车辆所处位置确定其移动顺序及目标位置,其决策变量为xi,m,r和ti,m,xi,m,r为0-1型变量,当车辆i存放在存储区域的m行r列的位置为1,未存放则为0;ti,m为连续型变量,表示车辆i在存储区域内m行转移的时刻。

(5)

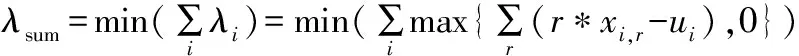
(6)

(7)

(8)

ti,m=r,∀i∈[1,S],m∈[1,M]

(9)

(10)

(11)

ti,m+1≤ti+1,m,∀i∈[1,S-1],m∈[1,M]

(12)

xi,m,r=1,∀i∈[1,S],m∈[1,M]
xi′,m,r+1=1,∀i′∈[1,S],m∈[1,M]

(13)

1+ti,m≤M(2-xi,mA,r-xi′,mA,r+1)+ti′,m,∀i,i′∈[1,S],
m∈[1,M2],mA∈[1,M1],r∈[1,R-1]

(14)

M*br≥|xi,r*ci,j-xi′,r+1*ci′,j′|
∀i,i′∈[1,S],r∈[1,S-1]

(15)

式(5)、式(6)为目标函数。式(5)为喷涂作业颜色切换次数之和。式(6)为喷涂作业集Q与下游生产需求序列的偏差成本。式(7)～式(12)为工序1的约束条件。式(7)代表在任意时刻,存储区域的m车道r车位至多可存放一辆车身,车辆数量限制。式(8)代表在任意时刻,车辆i进入存储区域必须具有存放位置,车辆空间存储限制。式(9)将车辆i在存储区域内转移的时刻以其在存储区域内m车道上的车位顺序号r表示,并将其进行线性化处理,得出式(10)。式(11)代表在任意时刻,线性存储区中同一车道内前面车位优先安排存放车辆,不存在间隔存放车辆的可能,线性存储方式约束。式(12)代表在任意时刻,线性存储区中因其同一车道路由顺序限制,顺序约束。

工序2与工序1约束相同,其先执行出库、再执行入库操作,增加式(13)、式(14)两个约束,放置在存储区域m车道上第r车位的车辆i可用式(13)第一个式子表示,放置在存储区域m车道上第r+1车位的车辆i′可用式(13)第二个式子表示,结合式(12)求解出式(14),两个车辆存放顺序约束。

工序3为车辆由存储区域进入输出队列,在基础之上增加式(15)约束,表示产生输出队列Q={q1,q2,q3…,qs},其队列中顺序为第r位的车辆与前一车辆颜色不一致时需换漆,换漆约束。

2 改进遗传算法设计

2.1 改进遗传算法流程

通过改进遗传算法的计算流程及编码设计方式,实现车辆路由控制。本研究针对多存储区划分多过程分别求解,将每个过程按照入库、出库操作区分,其中车辆入库基于启发式规则进行制定路由策略,车辆出库基于遗传算法寻找最优策略,如图3所示,改进遗传算法的具体执行步骤为:

步骤1:根据涂装车间待排列车辆及颜色属性进行编码设计,采用单层编码设计。

步骤2:根据种群初始化策略设定初始种群。

步骤3:进行交叉操作,采用GOX交叉策略,染色体长度为S,选取单位长度为3的基因段,寻找与其基因元素相同但顺序不同的基因段进行交换,进而生成新的子代,交叉操作流程如图1所示。

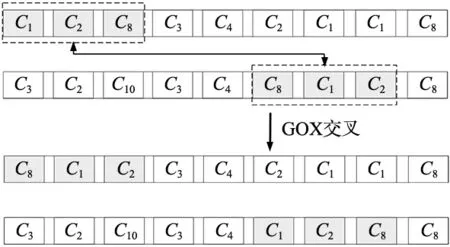
图1 GOX交叉策略流程

步骤4:进行变异操作,采用随机片段交叉变异方式,选取同一染色体上两个基因之间片段互换顺序达到随机变异的效果,产生新的子代,如图2所示。

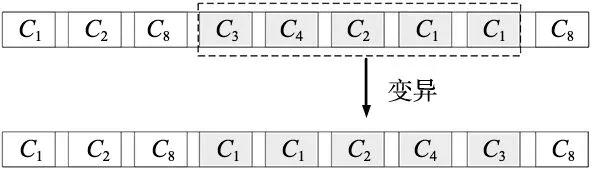
图2 变异策略流程

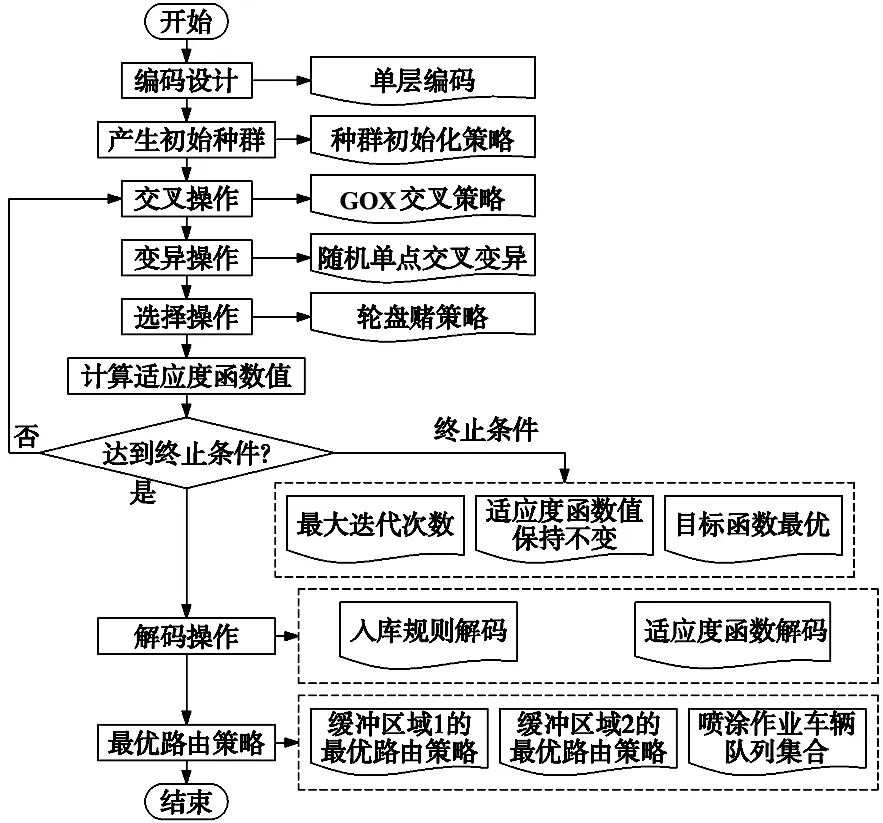
图3 改进遗传算法流程

步骤5:进行选择操作,采用轮盘赌策略进行子代选择策略。

步骤6:计算子代的适应度函数值。

步骤7:判断是否达到终止条件,若未达到终止条件,则返回步骤3产生下一次迭代,若达到终止条件则进行下一步操作。终止条件为:①最大迭代次数;②子代的适应度函数值连续多代保持不变;③目标函数达到最优。

步骤8:终止,根据入库规则及适应度函数进行解码操作。

步骤9:解码完成,得到路由策略B1、B2及喷涂作业车辆队列集合Q,完成一次求解。

2.2 编码设计

本研究采用基于车辆位置的单层编码方式表征,每条染色体的长度为待排列车辆队列长度S。每条染色体的排布代表车辆离开缓冲区域的一种出库方案,如图4所示,其中染色体上每一个数字代表车辆放置在存储区域所在车道m,且染色体上对应数字出现第r次就代表在该车道上第r顺序车位,每个基因代表缓冲区内m车道r车位的放置的车辆i,其排布顺序代表缓冲区对应车辆出库顺序。如bi,1,1代表缓冲区域内第一条车道第一个车位放置的车辆i,以此类推。

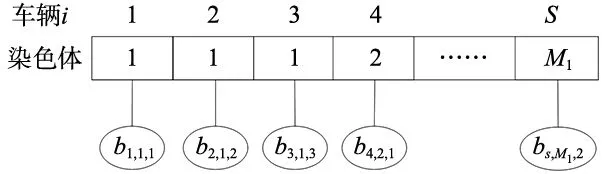
图4 染色体单层编码

2.3 解码设计

本研究的车辆入库过程基于启发式算法求解,车辆出库过程采用遗传算法求解,因此其入库操作的解码说明其启发式规则,出库操作的解码根据适应度函数结合编码表征。

(1)车辆入库启发式规则

①颜色匹配规则:设置车道颜色属性为最后进入车道的车辆颜色,当待排列车辆颜色与车道颜色属性相同时,选择该车道。

②颜色相同,车道号最小规则:当待排列车辆颜色与多个车道颜色属性相同时,选择车道号最小的车道。

③无颜色匹配,颜色数量判断规则:当待排列车辆颜色与所有车道颜色属性均不相同时,选择排除车道属性对应颜色的车辆已放完的车道。

④无颜色匹配,投票数最小规则:当待排列车辆颜色与所有车道颜色属性均不相同时,且车道属性对应颜色的车辆均未放完,选取待进入队列中m-1辆车,车辆颜色与车道颜色属性相同时车道投票数加1,选择投票数最小的车道。

(2)计算适应度值

针对本研究所涉及的3个工序,分别给出适应度函数。工序1和工序2为单目标,通过适应度函数表征;工序3为多目标,采用非支配排序求解Pareto集[18]。

(16)

(17)

工序1与工序2仅考虑颜色切换次数最少单目标,适应度函数以式(16)、式(17)表征。式(16)中θi,r代表存储区域内放置在r车位的车辆i是否需要切换颜色。式(17)为以颜色切换次数最少为目标建立的适应度函数。

工序3综合考虑涂装喷涂作业颜色切换与总装生产需求,为多目标优化,求解Pareto最优解集,将其映射到目标空间构成Pareto前沿,建立颜色切换次数和于总装生产需求偏差的二维目标空间,根据决策者偏好选择最优策略。

2.4 种群初始化策略

在遗传算法的计算过程中,入库操作的初始化种群规则已在解码设计中说明,针对出库操作的初始化种群策略主要如下:

(1)先进先出策略:按照车辆进入车道存放时间先进先出。

(2)颜色相同策略:车辆出库选取每个车道首部车辆,与出库前一车辆颜色相同车道出车,若多个相同颜色车辆,按照最小车道号顺序出车。

(3)颜色不同重寻策略:车辆出库选取每个车道首部车辆,与出库前一车辆颜色没有相同的情况下,寻找存储区内前m列,相同颜色的车辆向后排,相同颜色车辆越多出车顺序越靠后。

3 实例

3.1 背景

以某新能源汽车制造厂涂装车间为例,将多缓冲区联合路由调度结果运用到车间生产,构建车辆路由调度系统。该厂涂装车间内喷涂工位前设置两个缓冲区:缓冲区1为中涂存储区,设置5个车道、11个车位,可容纳55个车辆,即M1=5、R1=11;缓冲区2为分色存储区,设置5个车道、5个车位,即M2=5、R2=5,可容纳25个车辆。待喷涂车辆集合先进入中涂存储区排序,经移行机移动至分色存储区重排序,最后进入喷漆工位喷涂操作,工序1为由待排列队列进入中涂存储区,工序2为中涂区进入分色区,工序3为分色区进入喷涂工位,且设置一个机器人进行车辆颜色喷涂,该机器人不区分车型。喷涂完成车辆离开涂装车间进入PBS区域进行重排序,按照总装生产需求进入总装车间。根据该厂生产计划进行算例设计,生成3个算例,分别包含240、480和720个车辆。

3.2 结果分析

将3个算例分别代入改进遗传算法计算,为了便于展示结果,选取18个车辆表达路由策略,输入车辆队列已知为:

C={c1,6,c2,1,c3,2,c4,8,c5,7,c6,5,c7,1,c8,3,c9,4,c10,4,
c11,1,c12,2,c13,3,c14,5,c15,3,c16,6,c17,7,c18,6}

车辆总装生产需求已知为:

U={u2,1,u3,2,u4,8,u5,7,u17,7,u7,1,u11,1,u8,3,u9,4,
u10,4,u6,5,u14,5,u12,2,u13,3,u15,3,u1,6,u16,6,u18,6}

参数设置如下:种群大小N=200,交叉概率P=0.85,变异概率Pm=0.05,迭代次数T=300。

将已知待排序车辆集合通过改进遗传算法求解出来的可行解集采用非支配排序表征,分别在颜色切换次数及总装生产序列偏差两个维度进行表征,绘制两目标Pareo前沿如图5所示。

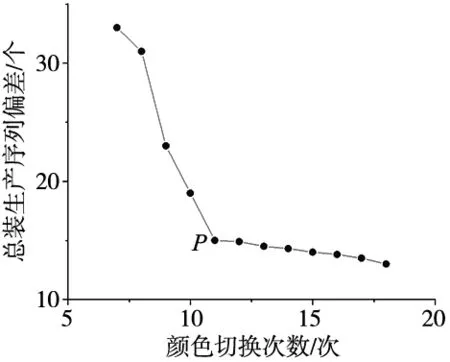
图5 两目标Pareto前沿

以图5中P点标识的路由策略说明,工序1以待排序车辆队列为已知输入,输出中涂存储区的车道及顺序集合,路由策略B1如图6所示。

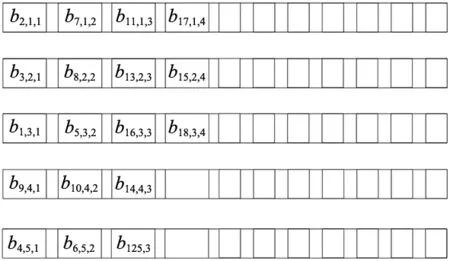
图6 中涂区车辆路由策略

针对车辆从中涂存储区进入分色存储区的工序2分析,其先执行出库操作,由移行机将中涂区车辆先移出库区,再执行入库操作,以中涂存储区车辆路由排布为已知输入,车辆调度的路由策略B2如图7所示。

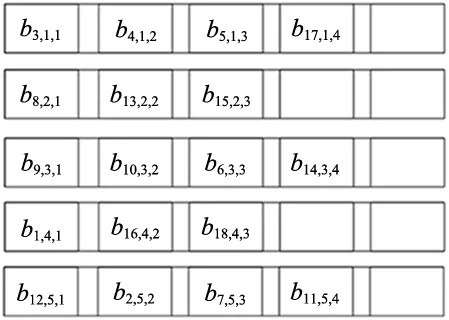
图7 分色区车辆路由策略

针对车辆由分色区进入喷涂工位产生输出车辆队列的工序3分析,其仅涉及出库操作,以分色存储区的车辆路由排布为已知输入,可求得喷涂工位处输出队列:

Q={q3,2,q12,2,q4,8,q5,7,q17,7,q2,1,q7,1,q11,1,q9,4,
q10,4,q6,5,q14,5,q8,3,q13,3,q15,3,q1,6,q16,6,q18,6}

其在可视化界面中展示如图8所示。

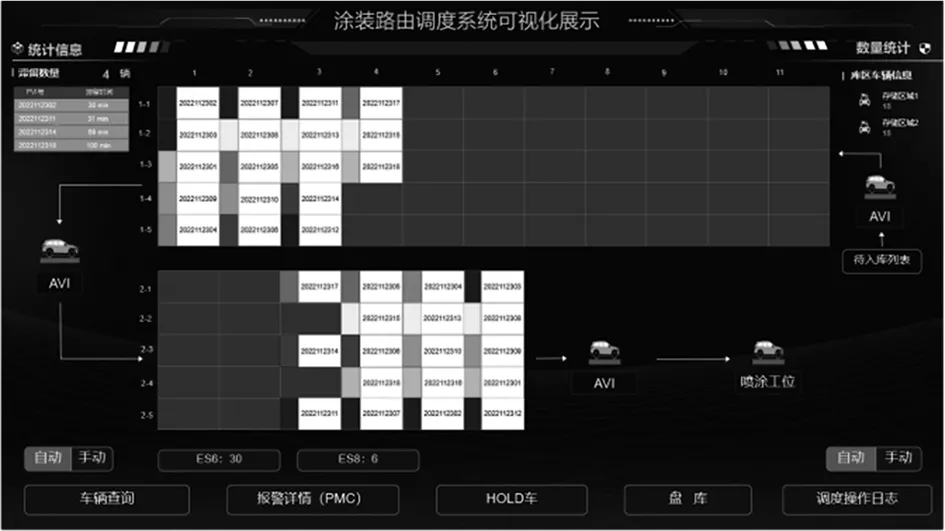
图8 涂装路由调度系统可视化界面

表3通过计算分别为240、480、720个车辆的算例,将使用改进遗传算法与未使用所产生的结果进行对比。

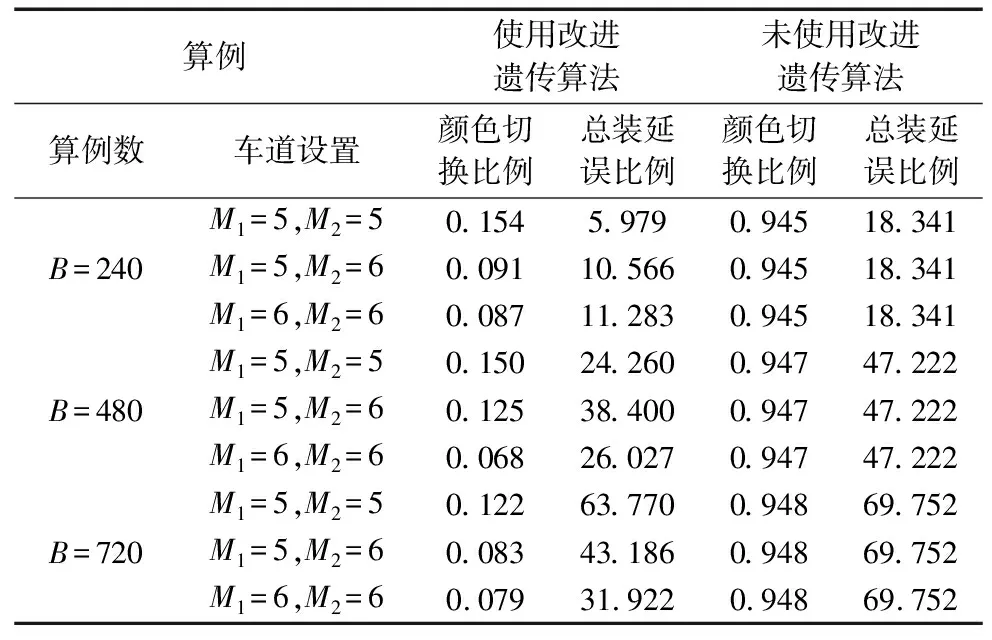
表3 不同算例车辆路由调度结果对比

通过3个不同规模算例在不同布局设置的缓冲存储区内使用与未使用本方法的路由策略在两个目标维度对比分析可知:

(1)在算例规模相同的条件下,缓冲区域内车道数设置越多,即缓冲区容量越大,使用改进遗传算法计算后的路由策略在颜色切换次数及总装生产需求延误两个目标维度上优化效果越优。

(2)在缓冲区域布局设置相同的条件下,在一定规模范围内,问题规模越大,本方法计算的路由策略与未使用对比的效果越显著。通过计算,在置信水平为0.95条件下,本系统可使涂装作业切换成本下降83.26%左右,总装生产需求偏差成本下降12.31%左右。

(3)使用本算法进行多存储区域联合路由调度与遗传算法进行单存储区路由调度[19]相比,在缓冲区域车道数量明显低于其的情况下,颜色切换比例维度下降43.38%左右,且总装需求延误维度也得到一定程度提升。

4 结论

本文针对涂装作业车辆在多个缓冲区的重排序问题研究,以最少化喷涂作业颜色切换次数及总装生产需求序列偏差最小为目标,综合考虑车间布局、时间、空间约束,将其划分为3个过程分别建立MILP数学模型,通过改进遗传算法结合启发式规则进行车辆路由调度,可得出结论如下:

(1)针对汽车生产过程,上下游需密切配合,将某一工艺独立研究意义不大,需综合考虑该工艺及上下游需求,进行多目标、多影响因素研究,综合考虑涂装与总装需求建立多目标模型,调度结果愈佳。

(2)针对车辆重排序问题,缓冲区域容量设置与颜色切换、下游生产需求延误在一定范围内成反比,缓冲区容量越大,同等条件下,车辆重排序在目标维度的表现上越佳。

(3)将车间内部多缓冲区域联合进行路由调度所产生的效果较单缓冲区路由调度可产生更优策略,增加重排序过程,可解决较大的规模问题,满足生产实际需求。

(4)通过改进遗传算法的计算流程及编码,结合启发式规则实现车辆重排序,可高效求解,产生更优策略。