基于信息融合的稀疏自编码故障诊断*

普会杰,刘 韬,褚 惟

(昆明理工大学a.机电工程学院;b.云南省先进装备智能维护工程研究中心,昆明 650500)

0 引言

机械设备在使用过程中会由于疲劳磨损、工作环境恶劣等问题,容易发生性能和健康状态的退化[1]。而滚动轴承、齿轮故障是大多数机械设备性能失效的主要原因之一,因此对滚动轴承、齿轮的故障诊断就显得尤其重要。

在故障诊断研究中,普遍采用信号处理与模式识别相结合的诊断方法[2],特征提取和模式识别是故障诊断的核心技术。如利用经验模态分解、小波分解等,提取特征并送入支持向量机、极限学习机等模型进行故障诊断。由于特征提取的部分参数和信号分量的选择等依赖先验知识,因此存在一定的不确定性。此外,传统分类模型的泛化能力不佳,输入特征的微调有时甚至会导致分类效果明显下降,而且当输入的特征维度较大时,分类器的训练也变得困难,模型训练效率变低。

近年来,深度学习被广泛应用到故障诊断,它利用机器学习的深度结构,自动学习高层次的本质特征[3],根据输入自动提取更具鉴别性的高层次特征,解决了传统提取特征的弊端。JIA等[4]结合机械大数据和深度学习理论,提出了一种新的机械装备健康监测方法。HU等[5]将降噪稀疏自编码用于风机转速预测。张绍辉[6]提出利用稀疏自编码深度学习模型对各个传感器采集到的数据进行融合,采用稀疏自编码与平方预测误差相结合的模型有效监测轴承故障,并对故障部位进行准确定位。汪鹏等[7]提出了一种基于参数稀疏自编码器的故障诊断方法,通过编码过程分析信号组成成分来判断旋转机械的故障。袁宪锋等[8]提出了一种基于栈式稀疏自编码网络、改进灰狼智能优化算法以及支持向量机的混合智能故障诊断模型,对不同滚动轴承故障类型的振动信号实现更精准的识别。张绍辉等[9]提出了一种基于频谱包络曲线的稀疏自编码算法,并用齿轮箱故障数据进行了验证,在保证诊断模型识别效果的同时,降低算法的计算复杂度,提高诊断模型的适用性。

自动编码器以其良好的特征提取和降维性能,被广泛应用于机械设备的故障诊断。目前大多数研究集中在将时域信号、频域信号直接输入到深度学习模型中或者人工提取特征后再将其送到网络模型,通过不断训练调整参数和人工调整来提高的模型泛化能力。但是,将时域信号直接输入深度学习模型,存在信号截取规则随机导致分类结果差异较大;而以频域信号作为输入,又存在频谱中各频段信息的有效信息不一致,降低了模型学习效率;包络谱低频信息虽然在一定程度上提高了计算效率,但变转速设备难以从包络谱里面提取到有用的信息,限制了该方法的应用。

因此,本文提出了一种基于信息融合的稀疏自编码故障诊断方法,充分利用振动加速度信号、速度信号、位移信号里的有效信息进行故障诊断,降低模型复杂度的同时,提高了诊断准确率和泛化性。

1 理论基础

基于信息融合的稀疏自编码故障诊断方法包括数据信息融合、稀疏自编码器和SoftMax分类器三部分。信息融合层次分为数据级融合、特征级融合、决策级融合[10]。数据级融合信号的特点是数据量庞大、维数繁多,且融合在底层发生,可以提供最完整的信息,精度属最高。3种融合关系如图1所示。

通过频域积分方法对原始振动加速度进行一次、二次积分得到速度、位移信号,并结合频谱信号,将3个信号进行数据层融合作为自编码器的输入。稀疏自编码器可视为一个深度自适应学习网络,可以无监督自适应学习特征。SoftMax分类器[11]将稀疏自编码器提取的特征经过非线性变换,输出分类结果。

1.1 信号积分转化

在进行信号采集的过程中,可能会受到仪器设备或环境等因素的限制,部分物理量往往要通过另外一些采集到的物理量进行转化,如将振动加速度信号转化为速度、位移信号。加速度传感器广泛用于获取振动信号,因为与速度和位移传感器相比,振动数据可以快速捕获,并且采集系统需要安装的附加设备更少。基于振动加速度信号,可以通过傅立叶变换和积分运算获得速度和位移信息[12-14]。常用的将振动加速度信号转化为速度、位移信号的方法有时域积分和频域积分两种方法。

1.1.1 时域积分

设采集到的振动加速度信号a(t)为:

a(t)=x(t)+ε

(1)

式中:ε是采集时产生的误差。

一次时域积分得到速度信号v(t):

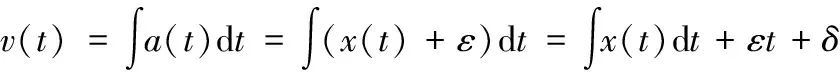
(2)

二次时域积分得到速度信号s(t):

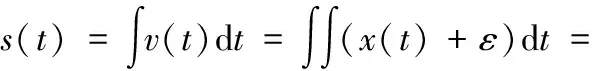
(3)

时域积分,方法原理简单,但多次积分后,测量误差ε的作用被放大,导致一次、二次积分得到的速度、位移信号与真实情况有很大偏差[15],位移振幅值将产生严重偏移趋势项,很大程度影响测量的准确程度。理论上加速度信号在时域上进行两次积分可以得到位移信号,但实际的结果不理想。

1.1.2 频域积分

频域积分算法是将时域数据通过傅里叶变换转换为频域数据,在频域中解决时域计算无法解决的响应问题,得到精确解[15]。积分在频域里积分的原理是:将信号做傅里叶变换,将变换结果在频域里做积分运算,最后做傅里叶逆变换得到积分后的时域信号。

加速度信号a(t)在某一频率的傅里叶变量形式表示为:

a(t)=Aejwt

(4)

初速度为0时,对加速度信号进行时间积分可以得到速度信号分量,即:

(5)

式中:V为速度信号分量v(t)对应的系数。

一次积分在频域里的关系为:

(6)

初速度和初位移分量都为0时,对加速度信号的傅里叶变量两次积分就能得到位移信号分量,即:

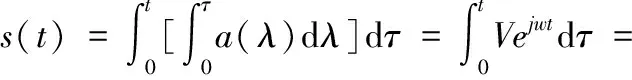
(7)

式中:X为位移信号分量s(t)对应的系数。

两次积分在频域里的关系为:

(8)

将振动加速度信号中所有不同频率的傅里叶分量按照积分在频域里的关系式计算后,进行傅里叶逆变换就能得到相应的速度信号和位移信号。利用频域积分的计算结果较时域积分算法会更准确,故选用频域积分算法来求速度、位移信号。

1.2 稀疏自编码器

自编码器是一种无监督自适应学习神经网络,由输入层、隐含层和输出层组成,通过对输入的编码和解码两个过程提取输入数据的隐含层特征,稀疏自编码器基于自编码器在目标函数的变化上加入系数惩罚项,通过稀疏惩罚项,提取稀疏的数据特征,有效降维并改善聚类的效果,自编码器的结构如图2所示。

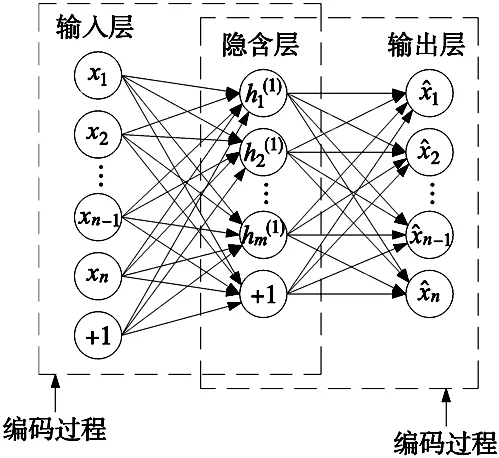
图2 自编码器结构图

编码过程:设输入的无标签样本数据为:{x1,x2,…,xn-1,xn},利用编码器激活函数fθ对输入数据进行编码转化为隐含层矢量hm,即:

(9)

(10)

式中:fθ的激活函数为tanh函数,编码层的权重矩阵和偏置参数为w和b。

(11)

式中:fθ′是解码层的激活函数,解码层的权重矩阵和偏置参数分别为w′和c。

在进行隐含层矢量重构的过程中,通过构建误差损失函数对网络的误差进行计算,从而得到最优的输出结果,损失函数J为:

(12)

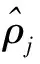
(13)

当神经元输出接近于1时表示活跃,输出接近于-1时表示是被抑制。

通过相对熵来测量2个分布之间得差异,引入相对稀疏性因子ρ,于是惩罚因子可以定义为:

(14)

在自编码器中加入稀疏性约束,将式(14)作为惩罚因子加入原损失函数J中。

1.3 基于信息融合的稀疏自编码故障诊断模型

基于信息融合的稀疏自编码故障诊断模型的方法流程如图3所示,主要包括数据预处理、模型训练和故障诊断3个过程,具体的做法如下:

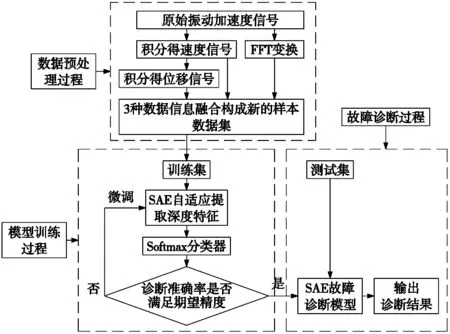
图3 基于信息融合的故障诊断模型的流程图

步骤1:数据预处理过程:将原始振动加速度时域信号a(t)经一次频域积分得到速度信号v(t),同时将原始振动加速度信号a(t)做快速傅里叶变换得到频谱信号,然后将一次积分得到的速度信号v(t)再经一次频域积分得到位移信号s(t),最后将频谱、速度、位移信号融合成一个复合信号作为样本数据集;

步骤2:模型训练过程:对融合后的复合信号划分训练集和测试集,通过构建的稀疏自编码网络进行无监督学习训练,自适应学习,得到深度特征向量;然后,将提取的深度特征向量送入SoftMax分类器进行故障模式识别,与真实标签进行对比后,若未达到期望的识别精度,则对模型进行微调直至达到期望的诊断准确率,保存训练好的SAE故障诊断模型;

步骤3:故障诊断过程:将划分好的测试集数据送入训练好的SAE故障诊断模型,输出诊断结果,完成故障诊断过程。

2 实验验证与结果分析

为验证所提方法的有效性和实用性,本文引入了滚动轴承故障实验数据和RV减速器行星轮故障实验数据进行验证。

2.1 滚动轴承故障诊断实例

滚动轴承故障实验数据选用某大学轴承振动加速度数据[16]。滚动轴承有正常、内圈故障、滚动体故障和外圈故障4种状态,3种故障状态下损伤直径又分为0.177 8、0.355 6、0.533 4 mm的3种损伤尺寸大小,故滚动轴承的故障实验数据有10种状态。

滚动轴承数据样本划分如表1所示。其中振动加速度信号的FFT变换后的频谱信号有1024个采样点,为了减少模型训练时间和探讨速度、位移信号融合对模型的有效性,对频域积分后的速度、位移信号只选取占频谱信息一定比例的长度来进行数据融合,即选取的速度、位移信号的点数占频谱信号点数的15%、30%、50%。

表1 滚动轴承数据样本集划分

2.1.1 滚动轴承故障诊断的步骤

首先,对滚动轴承加速度振动信号做一次、二次频域积分得到速度、位移信号,同时对振动加速度信号做快速傅里叶变换得到频谱信号,对频谱、速度、位移3种信号分别做归一化处理到[-1,1]。

其次,每个样本的频谱信号点数取1024,对速度、位移信号的点数长度只选取频谱信号点数的15%、30%、50%,即对速度、位移信号每个样本取154、308、512个点3种方式。

最后,为了对比不同输入对结果的影响,将划分好的样本数据集按照以下3种方式输入到稀疏自编码网络。方式1:归一化后的原始加速度信号;方式2:原始加速度信号作快速傅里叶变换后的频谱信号;方式3:频谱信号、速度和位移信号融合后的复合信号。方式3输入的复合信号的每个样本的长度有3种,取整后分别为1332、1640、2048。故障标签类型个数为10,所以3种输入方式的输出层神经元个数都为10,经稀疏自编码提取深度特征后,再通过SoftMax分类器输出诊断结果。

2.1.2 诊断结果

采用方式1、方式2输入的稀疏自编码网络分别构建了1、2、3层的网络模型,并对每种情况的诊断模型训练并测试了10次,取10次测试结果的平均值。方式1和方式2的在不同层数下的平均诊断率如图4所示。

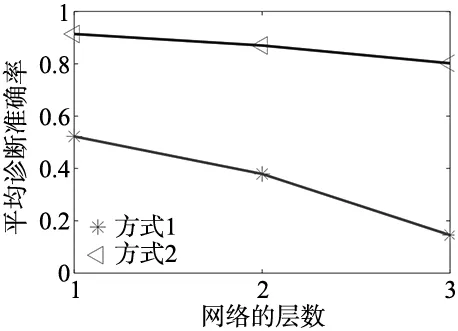
图4 方式1、2在不同深度下的平均诊断率对比

由图4可以看出,在不同的网络层数下,振动加速度信号的频谱作为输入,诊断准确率总是高于振动加速度作为输入的诊断准确率,这表明相比于振动加速度信号,频谱信号作为输入效果更好,但单独使用频谱信号作为输入,模型的诊断精度还有待提高。

利用t-SNE方法,对方式1、方式2、方式3提取的深层特征向量进行可视化,如图5所示。

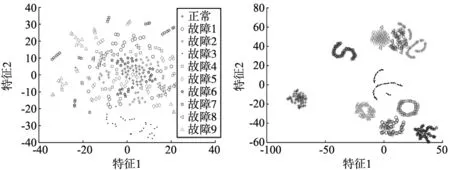
(a) 方式1输入 (b) 方式2输入

由图5可以看出,方式1输入,经稀疏自编码网络提取的深度特征散点图混叠,轴承的10种状态完全不可分;方式2输入,经稀疏自编码网络提取的深度频谱特征降低了不同状态的重叠程度,10种状态的特征散点图基本可分,但仍有极小部分划分错误,且3种不同故障尺寸的内圈故障之间的区分不够明显;方式3三种不同比例混合的复合信号作为输入,且只采用一层网络结构提取的深度特征,就能将轴承的10种状态完全区分出来。因此,频谱、速度、位移信号融合后提取到的深层故障特征更显优势,更适合分类器来做故障识别。

方式3输入中3种不同比例混合的复合信号,经10次测试后的平均准确率如表2所示。

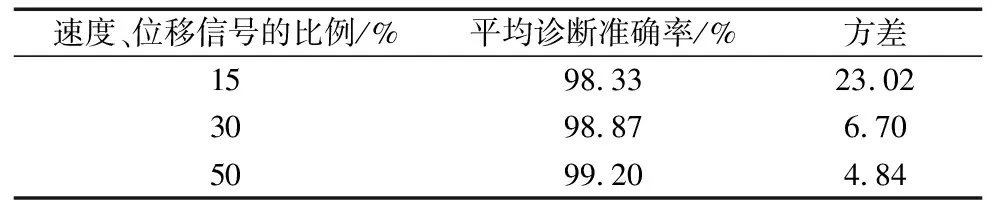
表2 方式3中3种不同比例混合的结果

由表2可以看出,输入的复合信号随着速度、位移信号信息量的不断增加,轴承的平均诊断准确率不断提高,并且方差也逐渐减小,说明速度、位移信号的信息增加会提高模型的稳定性,从而更加准确识别出轴承的状态。

2.1.3 对比分析

方式1中的振动加速度信号、方式2中的频谱信号和方式3中的3种不同比例混合的复合信号输入的诊断结果进行对比,利用测试集在这5种不同输入方式的故障模型上分别进行10次实验,方式1和方式2输入均选取诊断效果最好的层数模型结果进行对比,10次测试对比的结果如图6所示。

图6 5种不同输入方式10次测试的结果对比

将振动加速度信号直接输入到SAE网络的平均诊断准确率最低,仅为52.24%,方差为29.24;将振动加速度信号转换为频谱信号输入到SAE网络的平均诊断准确率为91.40%,方差为12.27;在频谱信号的基础上融合了速度、位移信号后,诊断准确率明显提高,平均诊断准确率分别为98.33%、98.87%、99.20%,方差分别为23.02、6.70、4.84。通过对比,可以得出结论:频谱信号融合速度、位移信号后,模型的故障诊断准确率会明显提高,且随着速度、位移信息量的增加,诊断模型的稳定性会更好。

2.2 RV减速器故障诊断实例

采用某大学工业机器人RV的实验数据[17]。RV减速器行星轮故障实验在RV减速器测试台上进行,实验台如图7所示。

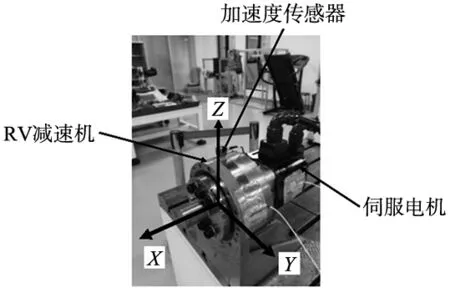
图7 工业机器人RV减速器故障实验台

RV减速器的实验数据选用减速器输出轴单向无负载的持续运动故障数据,RV的状态主要有5种:正常、点蚀故障、断齿故障、裂纹故障、磨损故障,故障主要发生在行星轮上。

故障数据样本划分如表3所示。同样对频域积分后的速度、位移信号只选取频谱采样点数的一定比例长度来进行数据融合,即选取速度、位移信号的点数占频谱信号点数的15%、30%、50%。

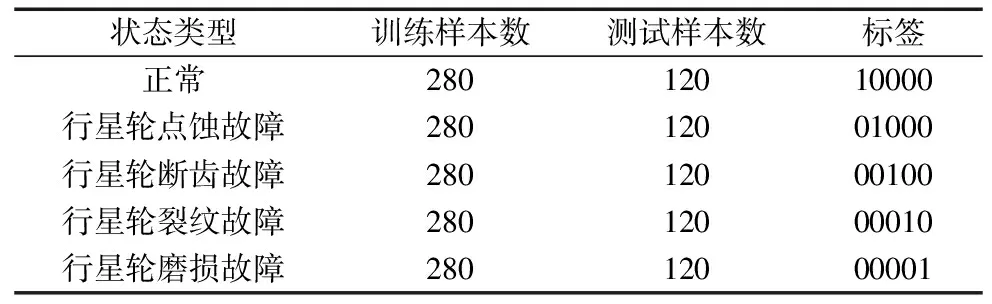
表3 RV故障数据样本集划分

2.2.1 RV行星轮故障诊断的过程

首先,对采集到的RV振动加速度信号做一次、二次频域积分得到速度、位移信号,同时对振动加速度信号做快速傅里叶变换得到频谱信号,对频谱、速度、位移3种信号分别做归一化处理。

其次,选取每个样本的长度为1875,且对速度、位移信号的点数长度选取频谱信号点数的15%、30%、50%,即取282、563、938个点3种方式。

最后,同样按照以下3种方式输入到稀疏自编码模型。方式1:归一化后的振动加速度信号;方式2:原始振动加速度信号做快速傅里叶变换后的频谱信号。方式3:3种不同比例的复合信号。方式1和方式2每类RV状态的样本数为280,每个样本的数据长度为1875。方式3输入的复合信号的每个样本的长度有3种,取整后分别为2439、3001、3751。RV的状态为5类,所以3种输入方式的输出层神经元个数都为5,经稀疏自编码提取深度特征后,通过SoftMax分类器得到最终的诊断结果。

2.2.2 诊断结果

同样对方式1、方式2输入分别构建了1、2、3层的模型,并对不同层数的诊断模型训练并测试了10次,取10次测试结果的平均值,方式1、2在不同层数下的平均诊断率如图8所示。

图8 方式1、 2在不同深度下的平均诊断率对比

图8中,在不同的稀疏自编码网络层数下,振动加速度信号的频谱作为输入的诊断准确率总是高于振动加速度作为输入的诊断准确率,但单独用频谱信号作为稀疏自编码的输入,诊断精度还未达到预期目标。

利用t-SNE方法,对方式1、方式2、方式3输入提取的5种深层特征向量进行可视化,如图9所示。

(a) 方式1输入 (b) 方式2输入

由图9a可以看出,将RV的振动加速度信号作为稀疏自编码网络的输入,提取的深度特征散点图除断齿故障呈聚集状态,其余4种状态完全不可分;图9b图输入频谱信号,提取出来的深度频谱特征改善了不同状态间的混叠程度,5种状态的特征散点图大致可分,但正常、点蚀、裂纹、磨损状态的特征散点图还存在部分混叠,且类间距并不大,同一种状态的聚集程度并不明显;图9c～图9e图在频谱的基础上分别融合了15%、30%、50%的速度、位移信息,3种情况下的特征散点图RV的5种状态都可以明显区分出来,且不同状态的类间距明显增大,同一种状态的聚集程度也有明显改善。因此,将频谱、速度、位移信号融合后作为稀疏自编码网络的输入来提取RV行星轮的深层故障特征是完全可行的。

2.2.3 对比分析

方式1中的振动加速度信号、方式2中的频谱信号和方式3中的3种不同比例混合的信号输入的诊断结果进行对比,在这5种故障诊断模型上分别进行10次测试,方式1和方式2输入均选取诊断效果最好的层数结果进行对比,10次测试对比的结果如图10所示。

图10 5种不同输入10次测试的结果对比

将RV的振动加速度信号直接输入到SAE网络的平均诊断准确率最低,仅为71.30%,方差为15.41;输入为频谱信号后,平均诊断准确率为94.20%,虽然识别准确率明显提升,但方差为19.93,模型的稳定性较差;在频谱信号的基础上融合了速度、位移信号后,3种不同比例的混合信号10次测试的平均诊断准确率均为100%。通过对比,可以得出结论:频谱信号融合速度、位移信号后,诊断准确率会明显提高,且频谱信号输入中只需要融入15%的速度和15%的位移信息量,诊断模型的精度就可以达到100%,且稳定性较好。为节省模型的训练时间,对于RV减速器行星轮5状态的故障识别,只需要融合15%的速度、位移信息量即可达到预期诊断目的。

3 结论

振动加速度信息、速度信息、位移信息能更全面包含设备状态信息,本文将三者进行数据融合,并利用稀疏自编码与SoftMax分类器构建深度学习网络,对滚动轴承、RV减速器行星轮进行状态识别,最终得出以下结论:

(1)稀疏自编码具有强大的特征提取和降维性能,可以自适应提取深层故障特征,能有效解决传统手工提取特征区分度差、代表性弱的问题。

(2)相比于单一数据输入,频谱、速度、位移信号进行数据融合后的复合信号作为稀疏自编码网络的输入,滚动轴承和RV行星轮的多组对比实验结果表明,相比经典方法,所提方法在保证识别准确率和降低模型复杂度的同时,有效提高了其泛化性。