基于DWT的PCA+SVM优化算法在人脸识别应用中的研究

刘 敏

(合肥财经职业学院人工智能学院 安徽合肥 230061)

PCA+SVM 是人们常用的面部识别算法，识别性能较好。但PCA+SVM 算法也需要提高识别精度，以应对大规模的人脸数据。所以，如何提高PCA+SVM 算法在人脸识别领域应用的精确度，是目前研究的一个重要方向。小波变换(dwt)是一种时频分析方法，具有多分辨率、局部性和优秀的压缩性等特点。小波变换可以将讯号分解为频率不同、时间不同的多个子讯号，从而实现讯号的降维和特性的抽离。所以通过小波变的方式优化PCA+SVM算法，可以增强人脸识别的精确度。

一、PCA算法和SVM算法原理

PCA+SVM 算法的基本思路是，首先利用PCA 算法将高维度的人面图像数据向低维度空间进行降维处理，再将降维处理后的数据送至SVM分类器进行分类处理。

（一）PCA算法。PCA算法是一种常用的降维方法，其基本思路是将高维数据通过线性变换映射到低维空间，从而达到数据维度的降低。在图像处理中，PCA算法可以通过对图像数据的协方差矩阵进行特征值分解来提取图像的主成分，进而实现对图像的降维操作。

假设有一个n 维的样本数据矩阵X，每个样本有m 个特征值，则可以通过以下步骤来实现PCA算法：

第一步：对数据进行中心化处理

计算出数据矩阵X每个特征值的均值，然后将数据矩阵X的每个样本向量减去其均值，得到新的中心化数据矩阵Y。

第二步：计算数据的协方差矩阵

协方差矩阵C可以从一个中心化数据矩阵Y与Y的转置矩阵YT与相乘得到。

第三步：特征值分解协方差矩阵

特征向量和对应特征值用特征值分解协方差矩阵C求得。

第四步:选取主成分

按特征值从大到小的顺序取前k 个特征量，组成投影矩阵w。

第五步：进行降维操作

降维后的数据矩阵Z由原始数据矩阵X乘以投影矩阵计算得来。

（二）SVM分类器。SVM 是一种二分类模型，其基本思想是将原始数据映射到高维空间中，然后在高维空间中找到使正负样本分离最好的最优超平面(surface)。在SVM 中，对于一个二分类题，假设训练集中有n个样本，每个样本以m维的特征向量表示，其中xi 表示第i 个样本，yi 表示该样本的类别标记，取值为+1或-1。那么SVM分类题的基础模型就可以表现为：

其中，C表示惩罚因子，b表示一个分类超平面的截距，w表示一个分类超平面的法向量，εi表示松弛变量。

二、DWT小波变换的原理

DWT变换是一种基于小波分析的信号处理方法，可以将信号分解为不同尺度的子信号，并且能够提取信号的局部特征。在图像处理中，DWT可以将图像分解为不同尺度和方向的子图像，适用于图像的多尺度表示和特征提取。

DWT的基本思想是将信号分解成不同的尺度，对各种尺度的子信号进行低通和高过滤。具体地，对于一个长度为N的信号x，可以进行J级DWT分解，得到J+1个子信号，其中第j级的低频子信号Lj和高频子信号Hj可以分别表示为：

其中，h、g 分别表示低通、高滤，L0 为原始信号，Lj 为第j级低频子信号，Hj为第j级高频信号，n为点索引。

三、基于DWT的PCA+SVM算法优化

（一）算法流程。本文提出的基于DWT 的PCA+SVM 算法优化方法的流程如下：

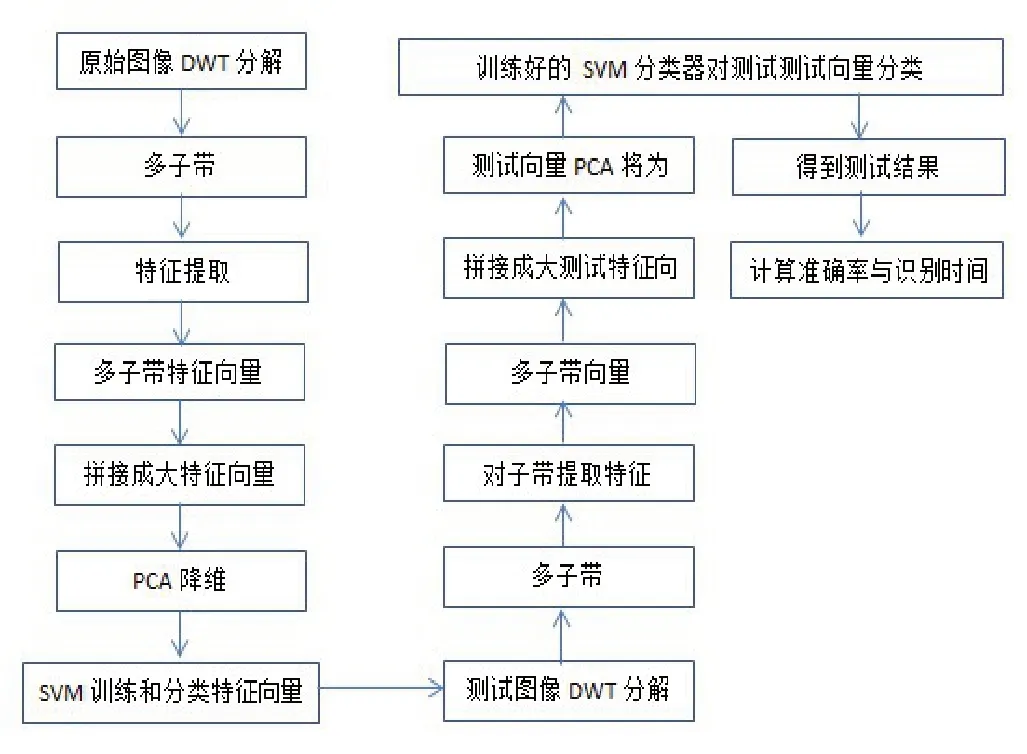
图1 DWT+PCA+SVM算法优化流程图

（二）算法实现步骤。本文提出的使用DWT 的PCA+SVM算法优化方法的具体步骤是：

1.用DWT分解原人的脸部形象为多条子带。DWT是一种多尺度分析方法，其基本思想是通过对信号进行多级低通和高通滤波，得到一系列尺度不同、频带宽度逐渐减小的子信号。在人脸识别中，将原始人脸图像分解为多个子带，可以有效提取图像的多尺度信息，提高人脸识别的鲁棒性。

假设有一个大小为N×M的原始人脸图像I，DWT分解的过程可以分为以下步骤：

Step1：将原始图像I分解为四个子图像

将原始图像I 分成四个子图像，即LH、HL、HH 和LL，其中LL子图像是低频子带，而LH、HL和HH子图像是高频子带。这个过程可以通过一个二维的 DWT 变换原始的图像来实现，得到如下公示：

其中，Lj+1、Hj+1、Vj+1、Dj+1分别表示第j+1 级DWT 变换的低频、水平高频、垂直高频和对角高频子带。

Step2：LL子图像再次分解

将LL子图像使用DWT再次分解，求得LL子图像的下一级分解系数。这个过程可以重复多个等级，直到子带的数量达到规定的要求。

Step3：重复Step1和Step2，得到所有的子带

对于其他三个子图像（LH、HL 和HH），可以重复Step1 和Step2 的过程，分别对这些子图像进行DWT 分解，得到对应的子带。

最终，将所有得到的子带拼接在一起，得到一个多尺度子带图像序列$D={D_1,D_2,...,D_n}$，其中n为子带数目。

实现这一步功能的主要代码在MATLAB软件中表示如下。

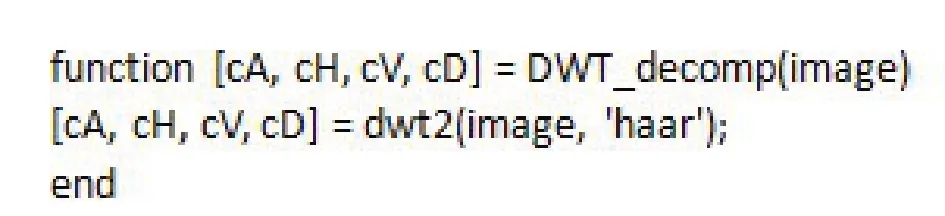
图2 实现相关功能的主要代码

2.对每个子带进行PCA降维操作，选取最重要的特征子集作为输入数据。对于每个子带，我们可以按照以下步骤进行PCA降维操作，并选取最重要的特征子集作为输入数据：

Step1：将子带重构成矩阵X：

其中，xi为子带中的一张人脸图像。

Step2：对矩阵X的各个列进行零的均值化处理：

其中，ui和σi分别为第i列的均值和标准差。

Step3：计算X的协方差矩阵C：

Step4：对C 协方差矩阵特征值的分解，求得特征值λ 和特征向量V：

Step5：按特征值由大到小排序特征向量，选择前k 位的特征向量作为特征的重要子集。

Step6：将重要特征子集组成的矩阵乘子带矩阵X，得出降维后的子带矩阵Y：

基于Matlab实现的PCA降维的主要代码如图3所示：

图3 实现相关功能的主要代码

3.把特征向量传入已训练的SVM 分类器进行分类。SVM分类器是一种二分类算法，可以将样本点划分为两个类别，例如“是”或“否”，“正”或“负”，“真”或“假”等。在人脸识别中，一般将SVM分类器用于将人脸图像分为“是该人脸”和“不是该人脸”两个类别。在使用SVM分类器前，先要对训练集进行训练，以确定SVM 分类器的参数，后在将特征向量传入SVM 分类器进行分类。

主要有以下几个步骤来进行SVM分类器的训练：

Step1：读取训练集数据：将训练集中的图像数据读入程序中，并将其转换为特征向量。

Step2：规范数据：对训练集合数据进行规范处理，以杜绝各特点之间的大纲差异。

Step3：SVM 分类器参数的确定：通过交叉验证等方法确定 SVM 分类器的参数，如惩罚系数，核函数参数等。

Step4：训练SVM分类器：利用训练集数据和确定的 SVM分类器参数对SVM分类器模型进行训练。

Step5：测试SVM分类器：将测试集合数据送到SVM分类器中进行测试，该分类器经过训练，计算识别率和准确度。

在执行上述步骤时，可以使用MATLAB 软件，调用其中的SVM 工具箱，对SVM 分类器进行训练和测试。下面是具体步骤：

Step1：读取训练集数据并转换为特征向量：使用imread()函数读取图像数据，并使用reshape()函数将图像矩阵转换为向量。将每个人的面部形象分别转化为一个matrix 中储存的特征向量。

Step2：标准化数据：使用zscore()函数对矩阵中的数据进行标准化处理，使各特征的均值为0，标准差为1。

Step3：确定SVM 分类器参数：使用fitcsvm()函数训练SVM分类器，并通过交叉验证等方法确定惩罚系数和核函数参数等参数。

Step4：训练SVM分类器：使用FitcSVM()函数对SVM分类器模型进行训练，并测试训练集数据使用Predict()函数。

Step5：测试SVM 分类器：利用Predict()函数将测试集合数据发送给训练良好的SVM 分类器进行测试，计算识别率和准确度。

（三）实验结果和分析。本文训练样本来自剑桥大学AT&T实验室创建的ORL人脸数据库中的图像，因为无论从形态、光线强度还是特征的几个关键点来看，这个人的人脸数据库中的图像都是标准化的，所以优化算法的实验不用预先处理图片，就可以直接使用ORL人脸数据库中的图片。在ORL人脸数据库中，部分人脸图像如图4所示：

图4 ORL人脸库中的图像

此次训练样本选择ORL人脸图片库中抽取了10个人脸后5张图片前5张为测试样张。选择10、20、30、40、50个重要特征向量为基，分别测试PCA+SVM 算法与本文提出的PCA+SVM优化算法基于DWT 的识别率进行比较，两种算法的识别率见表1。

表1 样本识别率

从图5可以看出，基于DWT 的PCA+SVM 多尺度人脸识别算法在识别准确率方面优于传统PCA方法。

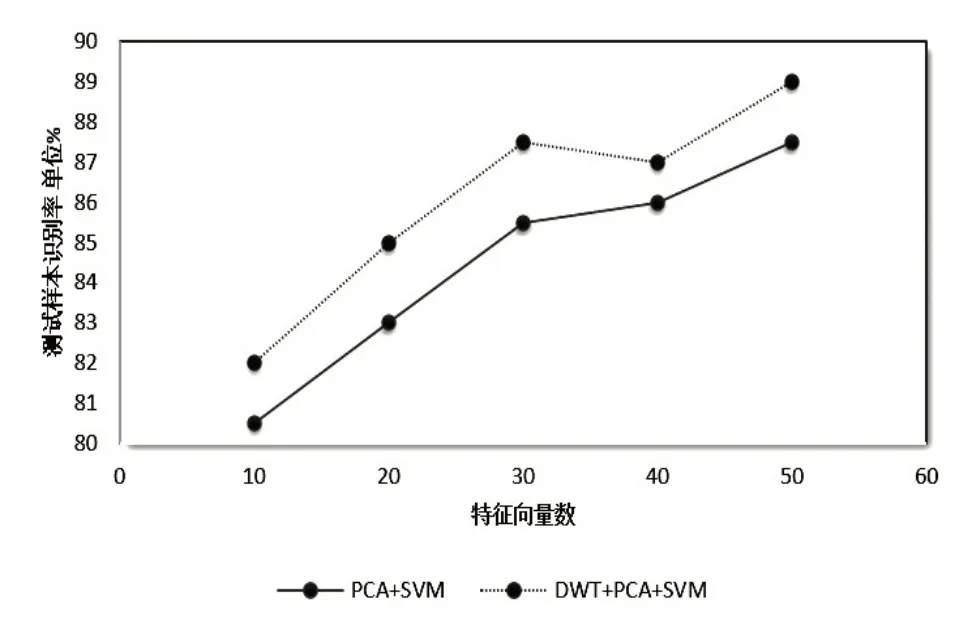
图5 两种算法识别率对比图

实验中将实训样本分为50%用于实训，50%用于验证；测试样张采用每人后5幅照片作为训练样张，剩余前5幅照片作为测试样张。识别率表示正确分类的测试样本数占全部测试样本数的比例，本实验使用的评价指标为识别率，识别率越高，说明使用的算法越优。从表1 和图5 中可以看出基于DWT 的PCA+SVM算法优胜于单纯的PCA+SVM算法。

四、结语

本文研究了基于DWT 的PCA 和SVM 算法的人脸识别方法，并对该方法进行了优化。通过DWT 将原始人脸图像分解为多个子带，然后对每个子带进行PCA降维操作，并选取最重要的特征子集作为输入数据，最后利用SVM分类器对人脸进行识别，从而实现快速准确识别面部特征。

实验结果表明，本文提出的方法在人脸识别精度上都传统的PCA+SVM方法更优。通过实验分析发现，DWT分解能够在一定程度上增加识别准确率，而PCA降维能够降低数据的维度和复杂度，提高分类的效率，最后通过SVM分类器能够进一步提高识别的准确性。

这项研究为人脸识别技术的发展提供了一种新的思路和方法，也为人类面部识别系统在实际应用中的应用提供了可行的解决方案。未来的研究方向可以在该方法的基础上进一步探索，如结合深度学习等新兴技术进行优化，以获得更好的效果。