开放大学统计课程融入Excel实例的教学实践探析

吴集林，陈燕平，姚家育，谢凡

（佛山开放大学，广东 佛山 528000)

0 引言

统计基础[1]或统计学概论[2]是开放大学经管类专业的必修课，是一门阐述搜集、整理、分析统计数据的方法论的科学，目的是探索数据的内在规律性，运用统计的思维去发现数据、分析数据。通过本课程的学习，学生掌握统计学的有关理论和方法，具有基本的统计思维，掌握搜集数据、整理数据、分析数据的方法。教材各章节的例子，是基于手工或计算器的工具来进行运算的，如果基于手工计算或统计，要耗费比较多的时间，并且容易出错。本来统计软件有SPSS、R语言、SAS等软件，但对于开放大学经管类的学生来说，并没有开设过统计软件的课程，计算机知识主要是学了计算机应用基础（含Word、Excel、PPT 等模块），没有其他的统计软件基础。其实，对于统计基础的实例，完全可以利用Excel实现。关于Excel在统计分析中的应用已有文献[3],但是文献主要是针对统计专业的学生而编写，难度相对大一些，本文根据开放大学经管类学生的特点，结合统计基础课程内容，有针对性地融入统计基础课程的实例的Excel实现。

1 统计分布数列

统计分布数列，也称分配数列、次数分布，是在统计分组的基础上，将总体的所有单位按组进行归类整理，形成总体中各单位在各组间的分布。体现形式的这样一个表格的内容一般是三列，第一列指的是总体按某标志值进行分组，第二列是各组分配的单位数（也称次数或频数），第三列是各组所占的比重（也称频率）。根据教材中做统计分布数列的过程，各组的单位数是在排序的基础上，一个一个手工统计的结果，其实在具体操作的时候，可用Excel实现。

首先介绍下面实例要使用的Excel函数countif的用法，

该函数的语法规则如下：countif(range，criteria)

第一个参数表示范围，第二参数表示条件，函数的功能是对指定区域中符合指定条件的单元格进行计数。

案例1：已知某班40 名学生的数学考试成绩，要求完成成绩的统计分布数列。

用Excel操作步骤如下：

1) 建一个Excel文件，在A列输入40个学生的成绩，输入完成后将成绩按升序排列，发现60分以下和90分以上的比较少，绝大部分在70至80之间，可将成绩分成5个组：60分以下，60～70，70～80，80～90，90分以上；

2) 在E列至G 做一个表，内容如下：

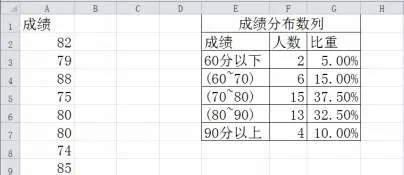
图1 学生成绩表的分布数列

3) 其中F 列和G 列的数据通过公式来实现，在单元格格F3 输入函数=countif(A:A,"<60")；在单元格格F4 输入函数=countif(A:A,"<70")-countif(A:A,"<60")；在单元格格F5 输入函数=countif(A:A,"<80")-countif(A:A,"<70")；在单元格格F6 输入函数=countif(A:A,"<90")-countif(A:A,"<80")；在单元格格F7 输入函数=countif(A:A,"<100")-countif(A:A,"<80")。

4) 在G3 输入公式=F3/40，并复制到G4、G5、G4、G7等 单元格格，G列单元格格格式为百分比。

本例的重点是掌握条件统计函数countif 统计某范围中满足某条件的数据的次数。

2 平均指标与变异指标

平均指标，又称统计平均数，主要用于反映社会经济现象某一数量标志在一定时间地点条件下达到的一般水平，平均指标有算术平均数、众数、中位数，其中算术平均数指的是总体标志总量除以总体单位总量的结果。众数是总体某一标志值出现次数最多的那个标志值。中位数指的是总体中各单位标志值按大小顺序排列，处于中点位置的标志值。变异指标反映总体某一标志值的变化程度，标准差是常用的变异指标，计算公式为，如果数据比较多，用这个公式来算，计算量也挺大的。

首先介绍下面实例要使用的几个函数的用法：

第一个函数average，语法规则为average (range),得到某范围中的数的平均数；

第二个函数mode，语法规则为mode(range),得到某范围中的数的众数；

第三个函数median，语法规则为median (range),得到某范围中的数的中位数；

第四个函数stdevp，语法规则为stdevp (range),得到某范围中的数的标准差。

案例2：已知某班40 名学生的数学考试成绩，计算算术平均数、众数、中位数、标准差等指标。

用Excel解题操作步骤如下：

1) 在A列输入40名学生的成绩；

2) 在D2 输入公式=average(A2:A41)得到平均成绩，D3 输入公式=mode(A2:A41)得到众数，D4 输入公式=median(A2:A41)得到中位数，D5 输入公式=stdevp(A2:A41)得到标准差。

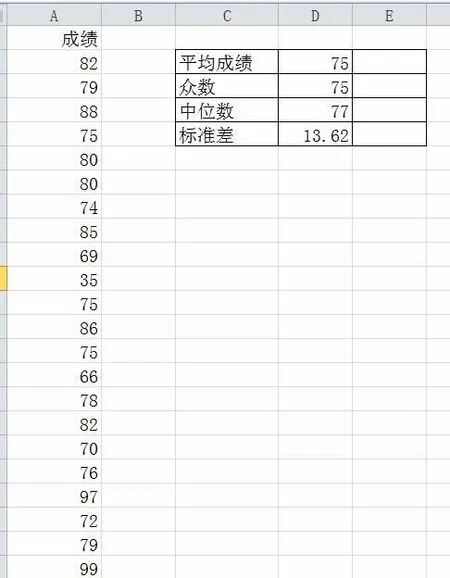
图2 学生成绩的平均指标与标准差

本例的重点是掌握众数函数mode、中位数函数median、平均数函数average及标准差函stdevp的使用。

3 相关系数与回归分析方程

相关系数指的是在线性相关条件下，说明两个现象之间关系密切程度的统计分析指标，通常用“r”表示，

回归分析是在相关分析的基础上，根据其变量之间的数量变化规律，运用一个相关的数学模型近似地表示变量间的平均变化关系，并进行推算和预测的一种统计分析方法。用直线方程来表示两个变量之间的变动关系，并进行推算和预测。一元线性回归方程：yc=a+bx，其中，不管是相关系数还是回归直线方程，如果用手工计算，计算量都挺大。但是利用Excel中的相关系数的函数和散点图表，可以很迅速地求得结果。

首先介绍下面实例要使用的Excel知识：

首先是理解函数correl，语法规则为correl (array1,array2)，得到两个数组的相关系数；

第二是通过插入散点图，并通过设置趋势线来获得回归直线的图像和直线方程。

案例3：有10 个家庭的月收入与消费支出如下，求月收入与消费支出的相关系数，并拟合消费支出对家庭月收入的回归直线方程。

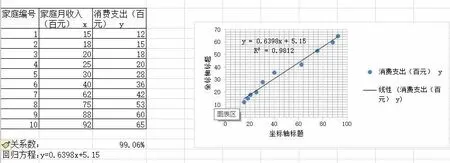
图3 月收入与消费支出的相关系数与回归直线图

用Excel解题操作步骤如下：

1) 在B 至D 列输入家庭月收入和消费支出的数据；

2) 在D15输入相关系数的公式=correl(C4:C13,D4:D13)，可迅速求得相关系数99.06%；

3) 先选择区域C4:D13,插入散点图，图表布局选择“布局3”，选择其中一个具体的点，右击，设置趋势线的格式，勾选“显示公式”和“R平方值”。

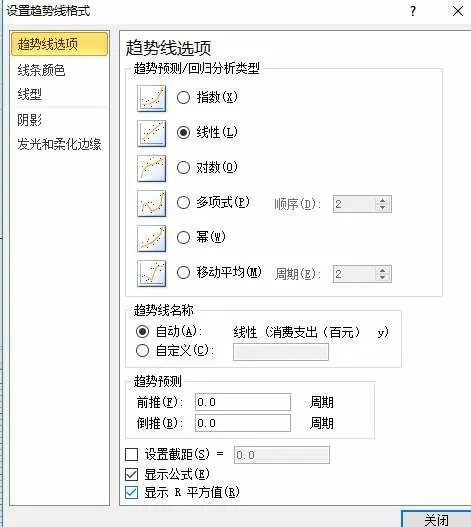
图4 设置趋线格式

于是图表区域中显示了回归直线方程和R 的平方，R的平方指的是相关系数的平方。

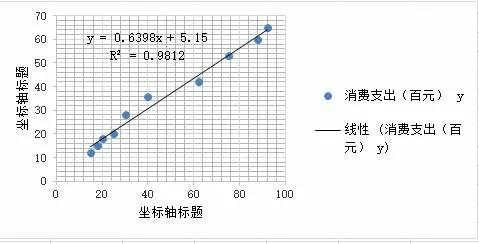
图5 回归直线与相关系数平方

本例的重点是掌握相关系数correl 以及利用散点图中的趋势线得到回归方程。

4 动态数列

教材的第八章是动态数列，讲一系列动态指标的计算，比如发展水平、平均发展水平、逐期增长量、累计增长量、环比发展速度、定基发展速度、环比增长速度、定基增长速度、平均发展速度。我们根据一个经济量的动态数列，利用Excel公式，可以迅速地计算一系列指标的数据。

案例4：根据我国1992年至2010年的国内生产总值，计算一系列的统计动态数列的指标，年份和产值为下表中的A列和B列的数据。

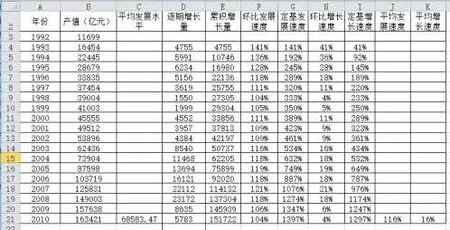
图6 统计指标动态数列

用Excel解题操作步骤如下：

1) 先从A列和B列输入年份和产值；

2) 求平均发展水平，在C21输入公式=average(B3:B21)；

3) 求逐期增长量 在D4 单元格格输入=B4-B3 ，并复制到本列的其他单元格格，因为是相对引用，被减数与减数引用的单元格会发生相应的变化；

4) 求累积增长量 在E4输入公式=B4-$B$3，并复制到本列的其他单元格格，因为被减数是固定的，所以要用绝对引用；

5) 求环比发展速度，在F4输入公式=B4/B3，并复制到本列的其他单元格。因为是相对引用，被除数与除数引用的单元格会发生相应的变化；

6) 求定基发展速度，在G4输入公式=B4/$B$3，并复制到本列的其他单元格，因为被除数固定，这里使用绝对引用；

7) 求环比增长速度，在H4输入公式=B4/B3-1，并复制到本列的其他单元格；

8) 求定基增长速度，在I4 输入公式=B4/$B$3-1，并复制到本列的其他单元格；

9) 求平均发展速度，在J21输入公式=(B21/$B$3)^(1/18)；

10) 求平均增长速度，在K21输入公式=J21-1。

本例的重点是在理解这一系列指标的概念，设置公式时先设置好最上的一个，注意公式引用的单元格是绝对引用还是相对引用，然后将公式复制得到一系列指标的结果，注意公式中哪些地方是绝对引用，哪些地方是相对引用，掌握绝对引用和相对引用的技巧[4]。

5 结论

本文根据广东开放大学专科统计基础或国家开放大学专科统计学概论中的章节内容，对于统计分布数列、综合指标、相关和回归分析、动态数列中的案例，用Excel中的公式或图表来实现，使得教学的重点放到主要理解概念和公式，而不是将大量的时间用在统计实例的演算过程，计算结果的求得用Excel 来实现，能大大简化计算过程的烦琐教学演示，这样既加深了对概念的理解，又提高了同学们利用Excel 解决实际问题的能力。