基于改进粒子群算法的AGV任务调度方法研究
杨铖,刘钰铭
(1.乌江能源投资有限公司,贵州 贵阳 550081;2.贵州大学现代制造技术教育部重点实验室,贵州 贵阳 550025;3.贵州省装备制造数字化车间建模与仿真工程研究中心,贵州 贵阳 550025)
0 引言
自动导引车(Automated Guided Vehicle,AGV)作为现代智慧物流中的重要工具,有力推动了传统企业向智能化、自动化方向转型和发展。目前,化肥农资产品以铁路运输为主,其运载环节采用传统的手工搬运和叉车搬运作业模式[1]。这种传统作业模式存在人力成本高、作业效率低下、自动化和智能化程度低等问题,难以满足当前化肥企业的需求。国内外学者对AGV任务调度方法展开了大量研究。Zou等人[2]通过构建多目标混合整数线性规划模型并利用多目标进化算法求解多品种小批量生产制造车间取送货的任务调度问题;Hu等人[3]对自动集装箱码头的AGV调度和存储分配问题建立了混合整数规划模型并通过基于贪婪的多阶段分解方法进行求解;石楠路等人[4]构建了考虑AGV换电过程的作业调度混合整数模型以减少等待时间,提高作业效率;霍凯歌等人[5]通过时间窗限制、负载均衡、现场实际情况等约束条件构建整数规划模型对生产运行总成本进行求解;颜骥等人[6]为解决多无人机多任务分配中的时序约束问题,扩展了分布式的一致性包算法;杨玮等人[7]以AGV执行任务的路径代价、时间代价以及任务均衡值代价为目标,建立多AGV仓储系统任务分配模型并提出了基于变邻域模拟退火的算法,提高了大规模任务下的求解精度和效率。尽管在各种应用场景中已有不少研究,但目前针对铁路化肥运载环节的相关研究尚在探索中。
因此,本文根据某化肥企业的实际需求,在化肥铁路物流运输的运载环节引入AGV 来探索高效率的智能物流作业模式,分析化肥站台运载作业的特点,确定以运载任务工作量均衡为主要调度优化目标并构建出对应的数学模型,提出基于混合策略改进粒子群算法(Improved Particle Swarm Optimization,IPSO) 求解任务分配调度问题,以提高作业效率,推动企业智能化转型,增强企业竞争力。
1 问题建模
1.1 问题描述
本文将在化肥站台堆区环境下的多AGV 任务调度问题分解为运载任务生成、匹配选择和分配三个子问题。假设火车有M节货厢,三种不同载重规格的货厢分别有a1、a2和a3节,当前在充电停靠区S的AGV群组中有K辆空闲可用的AGV。站台堆区多AGV 任务调度问题可以描述为:每次火车进站运载化肥,M节货厢产生N个任务需求Task(T1,T2,...,TN),其中每个任务Tn的载重量不超过AGV 的额定载重量w,表示不同规格货厢的任务基数且Task的数量N远大于AGV 的数量K。通过每次火车停靠的位置确定任务运载的目的位置,将化肥运载任务需求Task发布给各AGV,各AGV 接收到任务后从充电停靠区S出发,按照一定的执行顺序完成给定的运载任务。
从国外的资产评估人才培养模式中我们看出,无论是重视准入考试的美国还是重视高等教育的澳大利亚,其对资产评估人员的后续教育都一丝不苟。对后续教育未能完成的资产评估师的惩罚都十分严厉。我国的后续教育开展时间较短,处罚力度也相对较轻,造成许多资产评估师对后续教育相对敷衍。因此,我国资产评估协会可以成立专门的后续教育培训机构,负责我国资产评估师的后续教育的培训以及监管。除去正常的后续教育,各资产评估机构还应多开展关于资产评估行业的研讨会,和其他资产评估人员互相交流研究心得,互相促进对资产评估行业的理解。
1.2 模型构建
以某化肥企业站台堆区的运载环境为依据,通过栅格建模方法构建出化肥站台堆区的环境布局,规划示范点研究。该示范点的具体环境布局如图1所示,主要包括以下部分:1) 充电停靠区S:以S标记的栅格为AGV日常停靠和充电区域;2) 运载任务T:以T 标记的栅格为待运载的化肥;3) 任务目的地G:以G标记的栅格为化肥运载目的地,即火车货厢;4) 站台堆区结构柱:以O 标记的栅格为站台堆区的结构支撑柱,该结构柱位于运载任务T与运载目的地G之间且其不等间距分布;5) 行驶道路:站台堆区中的白色栅格为AGV的行驶道路。
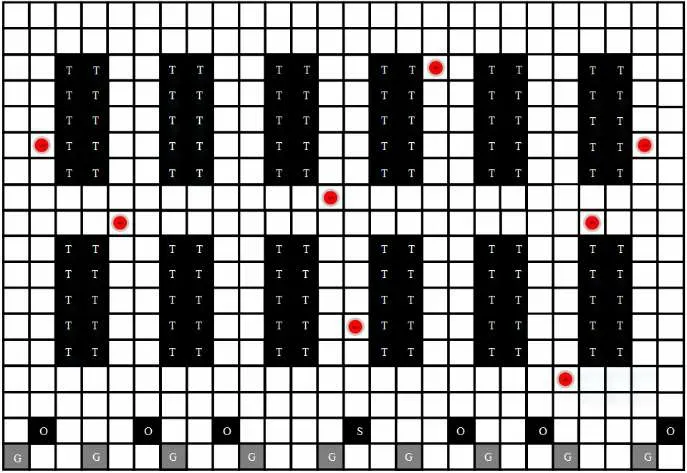
图1 化肥站台堆区示范点栅格地图
根据上小节问题描述,结合化肥站台堆区的实际情况,不失一般性,做如下约束与假设:1) 火车进站时全部AGV可用并且停放在充电停靠区S里;2) 任务的下达不受限制,即任一任务都可由任一AGV 执行;3)所有AGV 同质,不考虑化肥被运载至货厢后的情况;4) 每一运载任务有且只能由一AGV 执行,AGV 可以执行多个运载任务,但每个AGV必须完成目前所执行的运载任务才能去执行下一运载任务;5) AGV每次从S出发执行任务时电量充足且AGV 在运行过程中无需充电;6) AGV 执行任务过程不可中断,不允许出现任务中断或者任务变更的情况;7) 站台堆区上的化肥都已码垛整齐堆放在相对应的位置上并且每个位置上的化肥重量相同,不超过AGV 的额定载重量;8) 站台堆区上的结构柱不会阻挡火车货厢厢门,影响运载任务,即所有货厢均能正常进行货物装载工作;9) 不考虑化肥被运载至货厢后的情况,即不考虑化肥在货厢内的卸载情况。
根据对站台堆区化肥运载问题的描述与分析,多AGV任务调度问题所定义的符号和变量如下所示:
1) 符号、集合和参数定义
免耕播种技术是农机和农艺有效结合的重要产物,是一次技术的改革。农业生产过程中,积极推广应用免耕播种技术具有保墒、增加土壤肥力、减少土地流失、抑制土地荒漠化、降低作业劳动强度、减少成本投入等显著的效益。
①M表示火车每次进站的货厢数量表示总的运载任务数;S表示AGV充电停靠区;K表示参与运载任务的AGV总数量。
步骤4:采用实数编码的编码方式对任务进行编码,并通过基于Circle 混沌反向学习的种群初始化策略生成初始解集。
②fd表示权重因子,d∈{ }1,2 ;ae表示不同规格货厢的数量,e∈{}1,2,3 ;av表示不同规格货厢的任务基数,v∈{1,2,3} ;ωq表示单位代价系数,q∈{1 ,2} ;πk表示AGVk执行运载任务的序列;x表示AGV 的调度方案,x={π1,π2,...,πK}。
③h表示每次火车进站每节货厢的编号,h=1,2,...,M;i,j表示运载任务索引号,i,j= 1,2,...,T;k表示AGV的索引号,k= 1,2,...,K;g表示站台堆区中每一托盘的化肥重量。
步骤7:重新计算种群里各个粒子的适应度值,并确定和更新各粒子历史最优位置和群体全局最优位置。
⑤dki,j表示AGVk 在运载任务i和运载任务j间的空载成本代价,其中i≠j;dki,h表示AGVk将任务i运载至货厢h的重载成本代价;dkS,1表示AGVk从充电停靠区S到首个运载任务的成本代价;dkp,S表示AGVk最后一个运载任务p到充电停靠区S间的成本代价。
尼康为这款产品开发和制造的快门单元,其快门叶片是由碳素纤维和复合材料制成。对组装好的相机快门进行循环测试证明,D700相机的快门在极端环境中经过约150000次的测试。自我诊断式快门可持续地监控并保持快门的精确性。
yikh表示0-1决策变量,若AGVk将任务i运载至货厢h则为1,否则为0;zkij表示0-1决策变量,若AGVk执行完任务i后执行任务j则为1,否则为0。
河道基坑在开挖前,相关人员必须做好图纸审查要求,对于施工图纸审查核实设计要求,在接近建基面时,不可再用大型挖机开挖,宜使用小型挖机或人工挖除,在保证不惊扰建基面以下的原地基情况下,展开施工。
根据问题描述和相关符号定义,建立以运载任务工作量均衡、运载任务总代价为双重优化目标的数学模型,具体表示如下:
站台堆区多AGV 运载任务的分配问题是典型的NP-hard 问题,难以利用传统的数学方法在短时间内得到问题的精确解。本文设计了一种改进粒子群算法,用来解决站台堆区多AGV 任务分配问题,以便为各AGV 合理分配运载任务,得到全局近似最优分配方案。
动机性访谈能够增强患者的自我效能感的原因在于:(1)护理人员将患者的当前行为与期望之间冲突有效扩大,以此引导患者进行自我理性思考;(2)采用开放式的方式和相关访谈技巧增进了护理人员与患者之间的和谐关系,引导了患者理性思考;(3)跨理论模型能够充分理解患者,并对患者改变的动机予以肯定,让患者更为强化改变现有行为的意愿[16-17]。
其中,式(1)定义了目标函数,即求解最小总成本代价和最小化各AGV 运载任务的工作量差距;式(2)表示每次火车进站所有AGV的总运载任务代价成本;式(3)表示各AGV运载总重量均衡;式(4)表示AGVk运载任务自身成本代价和任务间的关联成本代价;式(5)表示AGV 将任务i运载至相对应货厢h的欧式距离;式(6)表示AGV执行完任务i要去执行任务j间的欧式距离;式(7)表示每次火车进站各AGV 运载任务的总重量;式(8)表示每次火车进站AGV 运载任务的平均重量;式(9)、(10)表示一个运载任务只能由一辆AGV执行;式(11)表示全部运载任务都分配给到相对应的AGV执行。
2 基于混合策略的改进粒子群算法
约束条件为:
2.1 任务粒子的编解码设计
为建立粒子群算法与站台堆区多AGV 任务分配问题的映射关系,本文设计了一种实数编码方案,粒子的每一位置代表着一种候选的任务分配方案,粒子位置的每维分量表示一个运载任务需求,通过求解最优粒子位置,可得到最佳任务分配方案。每一候选任务分配方案中包含两方面的信息,一个是任务对应的AGV序号,另一个则是任务执行的顺序。粒子编码如式(12)所示。
Xi为粒子群中第i个粒子位置,表示一种任务分配的方案;J表示运载任务总数;xij为第i个粒子位置的j维分量,代表着某一运载任务,其中,xij为实数,满足1 ≤xij 初始种群的优劣在一定程度上影响着任务分配方案的质量,传统的种群初始化方法容易导致后期种群多样性丧失,陷入局部最优。为保证初始种群的多样性,增强算法寻优能力,尽可能得到全局最优解,本文提出了基于混沌反向学习的种群初始化方法,先利用混沌模型生成初始粒子种群,改善初始种群粒子的分布情况,提高种群粒子个体的多样性,然后,通过反向学习方法进一步丰富种群的多样性,提高种群的质量,增强粒子群算法的全局探索能力。混沌序列初始化的主要思想是利用混沌其自身强随机性、非周期和多样性的特性,将初始解通过映射变换至混沌变量域,利用混沌模型方程产生混沌序列,然后再将混沌序列线性地映射回到原优化变量空间。本文采用Circle混沌模型[8]对粒子种群进行初始化,其映射定义表达式如式(13)所示: 种群初始化具体步骤为:先通过Circle 混沌映射模型生成粒子种群P,接着对混沌种群P中的每一粒子个体利用反向学习方法构建粒子反向种群RP,然后计算粒子种群P和粒子反向种群RP中每一个粒子个体的适应度值并对适应度值进行排序,最后,从粒子种群P和粒子反向种群RP的综合排序中选择适应度较优的个体组成粒子初始种群Pop。 尽管现在从语义网上提取信息的技术有了很大的进步,但是产生的RDF知识库仍然存在大量的噪音和与事实不一致的问题,需要添加一些额外的一致性约束。本节就是根据扩展的有效时间的现实意义,分析时态RDF数据存在的不一致性,根据不同情况进行了分类,并对存在的所有类型的不一致性提出修复算法。 在粒子群算法中,惯性权重系数ω在平衡全局搜索和局部开发方面发挥着重要的作用。因此,为了更好地提高算法性能,本文采用自适应非线性更新策略来调整惯性权重ω的值,具体如式(14)所示: 其中,ωmin和ωmax为惯性权重基准的初始值和终止值;t为当前迭代次数;Tmax 为算法设定的最大迭代次数;a,b和c为正数,作用于惯性系数非线性更新;通过惯性权重系数变化曲线图可以看出,权重系数自适应非线性更新策略在迭代前期一定时间内保持较大的值,增强全局搜索能力,以便能在解空间寻找更多可能的最优解区域;在迭代后期保持较小值的同时减小幅度变化,提高局部搜索性能,更快收敛到最优解。通过自适应非线性更新权重系数很好地平衡了粒子群算法的全局和局部搜索能力,兼具收敛速度的同时有效地提高了粒子群算法的收敛精度,避免局部解的产生。 粒子群算法在经过多次迭代后,大量种群粒子会出现趋同性,发生聚集现象,容易导致算法陷入局部最优。为解决该问题,提出基于差分学习的粒子变异策略来对粒子进行变异扰动,增加种群的多样性,扩大粒子的搜索广度,跳出局部位置,以增强算法全局寻优能力,其主要根据种群聚集程度对全局极值粒子采用差分进化算法中变异和交叉双重操作生成新的全局极值位置,用以替代历史全局最优位置,具体操作如下: 首先,计算每代粒子种群的适应度方差σ2,种群适应度方差σ2可以反映当前种群的多样性和聚集程度,当σ2越大时,种群粒子就越分散,种群多样化越大,不易陷入局部解,反之,当σ2越小时,陷入局部解的概率越高[9];其种群适应度方差计算如式(15)、(16)所示: 其中,N表示粒子种群的规模大小;Fi表示种群中第i粒子的适应度值;Fmean为当前粒子种群的平均适应度; 然后,当种群适应度方差σ2小于预设定扰动阈值ε或者连续it次迭代全局最优粒子gbest的适应度值不变化时,利用差分进化算法中的差分变异算子对全局最优粒子产生偏差粒子DP=(dp1,dp2,...,dpD),其变异表达式如下式(17)所示: 其中,gbest=(gbest1,gbest2,...,gbestD)为当代种群中最优粒子位置;F为缩放因子;X=(x1,x2,...,xD)和Y=(y1,y2,...,yD)为当代种群中随机选择且相互不同的粒子个体; 最后,利用差分进化算法中的交叉操作将偏差粒子DP与种群最优粒子gbest在每一维度以一定概率选择变异,最终实现对全局极值粒子的变异操作: 其中,Newgbestd代表变异全局最优解每一维的值。 采用IPSO算法求解多AGV任务分配问题的具体步骤为: 步骤1:确定火车进站货厢数量、停靠的位置和AGV的数量。 2) 决策变量 步骤8:判断是否需要进行全局最优位置变异,若需要,则采用基于差分学习的粒子变异策略,更新全局极值位置;否则转步骤9。 步骤3:设置算法参数,包括种群规模Ps、最大迭代次数Gmax,权重系数ω、学习因子c1,c2、扰动阈值ε、最大停滞迭代数it等。 不论是中国还是西方,都有对于“洪荒”的记录,洪水爆发,世界变得一片荒凉。因此笔者认为也可以利用中西方对于“洪”的相同文化认知,将“洪荒之力”译为“the power of the Flood”,除此以外,“洪荒之力”代表可以毁灭世界的力量。而在西方神话中,我们也可以找到与花千骨相对应的“妖神”,那就是海神Tethys。泰西斯是希腊神话中的海之女神。在早期神话中,她是一位创世女神,因此我们也可以利用Tethys这一意象,将“洪荒之力”译为“thepowerofTethys”。 步骤5:计算种群里各个粒子的适应度值,并确定和更新各粒子历史最优位置和群体全局最优位置。 步骤6:利用权重自适应非线性更新策略更新惯性权重系数ω,更新种群每个粒子速度和位置。 ④xi表示运载任务i的横坐标;yi:运载任务i的纵坐标;xj表示运载任务j的横坐标;yj:运载任务j的纵坐标;xh表示火车货厢h的横坐标;yh:火车货厢h的纵坐标。 步骤2:根据运载任务生成和选择环节确定总任务量和每个任务与货厢间的匹配关系。 步骤9:迭代次数更新G=G+ 1,判断是否达到终止条件G≤Gmax,若未达到,则转步骤6,反之,则算法终止,输出最优解。 混凝土碳化是指混凝土在水化过程中生成物Ca(OH)2与空气中的CO2再次反应生成CaCO3和水,导致水泥浆体中碱度下降和水的损失,从而引起混凝土开裂和钢筋锈蚀。引起混凝土碳化主要因素有组成混凝土的各种主要材料以及混凝土的配合设计。所以,在预防混凝土碳化的主要措施有:尽量减小水灰比,以减小单位体积混凝土的水泥用量;同时尽量选择低钙、低碳水泥和粉煤灰,降低混凝土的碳化反应;最后,应合理确定外加剂的掺量,使混凝土碳化影响减至最小。 步骤10:对求解的最优解进行解码操作,得到站台堆区AGV任务分配最佳方案。 2018年10月20日,中国—中东欧国家图书馆联盟在杭州正式成立,通过《中国—中东欧国家图书馆联盟成立宣言》和《中国—中东欧国家图书馆联盟2019—2020年行动计划》,联盟秘书处设在杭州图书馆。联盟成立后,各成员将在书目数据共享、文献交流互换、人员交流与培训、文化交流等方面展开合作,共同推进中国与中东欧各国图书馆的持续发展。 以图1所示的化肥站台堆区示范点为仿真实例对IPSO求解站台堆区多AGV任务分配问题的有效性和优越性进行验证。仿真实验中的算法均采用Matlab2020b 软件编程,测试环境为AMD Ryzen7-4800H@2.90GHz 处理器,16G RAM、64 位的Windows 10操作系统。 (六)牧草种植及秸秆青贮等加工利用情况 2011年全县发放优质黑麦草、甜高粱、青贮玉米和三叶草等优质牧草大约3吨,种植牧草近3 000亩。目前秸秆利用率较低,2011年仅利用玉米秸秆700亩。青贮技术尚未广泛应用。 为验证IPSO算法求解站台堆区多AGV任务分配问题的可行性,本文假设3辆AGV在示范点中执行20个运载任务,其中运载任务的位置和货厢的位置在站台堆区示范点随机生成,具体任务如表1所示。 表1 算法运行时间 IPSO算法求解站台堆区多AGV任务分配问题的适应度变化曲线如图2 所示,任务分配结果如表2 所示。从适应度变化曲线图中可以看出IPSO算法收敛速度较快,在迭代到第20代附近时即可找到问题的可行解,并且在迭代后期粒子通过变异策略能够跳出局部最优,让算法具有较强的寻优能力;从任务分配结果可知,IPSO算法能够很好地均衡每个AGV的任务,在兼顾任务数量均衡合理分配的同时也保证各AGV执行任务代价相对均衡,避免过大代价差异。由此,通过该实验验证了IPSO 算法求解站台堆区环境下AGV运载任务均衡分配问题的可行性。 表2 任务分配结果 图2 IPSO算法适应度变化曲线图 为验证IPSO算法求解站台堆区多AGV任务分配问题的优越性能,本文首先在三种不同条件的仿真场景下将本文改进粒子算法(IPSO)和基础粒子群算法(PSO)、遗传算法(GA)、基于概率分层的简化粒子群优化算法 (PHSPSO)、社会学习粒子群优化算法 (SLPSO)以及基于自适应策略的改进粒子群优化算法 (MPSO)进行对比仿真实验,其中,场景参数如表3所示;然后进行不同AGV数量下的算法性能对比,最后进行不同任务规模下的算法性能对比,进一步验证所提算法的优越性。上述仿真实例的任务在站台堆区示范点中随机生成。 为尽可能避免算法随机性的影响,每种算法在10、30 和50 任务规模的仿真实验条件下独立运行30次,且以1 000次最大运行迭代次数为算法终止条件。表3统计了在A1、A2和A3仿真场景中,六种算法任务分配方案的数据结果,表中列举了不同算法求解分配方案的适应度值的最优值Fmin、最差值Fmax、平均值Favg和标准差Fstd,以及分配的成功率P,其中分配的成功率是指满足约束条件的任务分配方案次数与实验总分配次数的比值。图3 是六种算法在A1、A2、A3仿真实验中平均适应度的收敛曲线。 从A1、A2 和A3 三组实验结果可知,六种算法中的IPSO 算法和MPSO 算法在三组实例中能合理分配任务,其成功率达到100%,而其他算法在随着任务规模的增加和AGV 数量的变化任务规划的成功率均出现了不同程度的降低。相较于其他对比算法,虽然IPSO 算法在Fstd和Fmax 指标上不是每次最优的,但其整体性能表现出一定的优越性,能得到最优的Fmin 与Favg,并且具有较快的收敛速度。上述仿真结果表明,IPSO算法能在不同条件约束下有效解决站台堆区多AGV任务分配问题,规划出质量较高的分配方案。 (3) 在塔-线体系导地线和杆塔同时发生共振时,同阶共振的两个相邻单塔会出现共振方向相同和相反两种振型形式.在同阶情况下,与单塔模态频率相比,塔-线体系中的单塔共振频率值要小,而且垂直向要比水平向更加明显. 通过分析可知,任务的规模决定了算法粒子求解的维度,随着任务量的增加会使算法粒子的维度不断增大,从而导致算法寻优的难度剧增;而AGV 的数量决定了算法粒子每一维度的上下限,随着AGV数量的增加会使算法粒子的搜索空间不断扩大,导致算法需要更强的局部搜索能力,以确保能搜索到可行解。因此,为进一步验证IPSO算法的优越性,进行不同任务规模下的算法性能对比实验和不同AGV 数量下的算法性能对比实验。其中,不同任务规模的算法对比实验条件为:在站台堆区环境下选取10 辆AGV 分别进行30、40、50、60、70 和80 规模的运载任务,算法终止条件为迭代1 000 次,每种算法在不同任务规模的仿真实验条件下独立运行30 次;不同AGV 数量的算法对比实验条件为:在站台堆区环境下分别选取3、8、10、20、30、50辆AGV执行60个任务,算法终止条件为迭代1 000 次,每种算法在不同任务规模的仿真实验条件下独立运行30次。表5和表6为不同任务规模和不同AGV数量条件下的实验结果。 ①灰狼优化算法的初始化种群个体是随机产生的,在一定程度上不能保证初始化种群的多样性,导致优化结果精度不高。本文算法的初始点是由定位数学模型计算出的初步定位结果以及离未知节点最近的信标节点的坐标产生,缩小了可行解空间,减小了计算量,同时加快了收敛速度。 水磨石地面通常遇到的典型问题是开裂,如果使用伸缩缝,受损情形可能只局限于部分区域.小且浅的裂缝可暂时不作处理,随着裂缝的加深和范围变大,有必要移除裂缝周边的受损材料,然后采用兼容的水泥浆或环氧树脂填隙[8].如果修补区域表面积较大,则需要分析原水磨石中的水泥强度等级,骨料种类、粒径、级配,制备成与原水磨石相近的原料进行嵌补,正式操作前应进行比对,若存在色差,则需要加入调色剂.嵌补之后进行机械磨光处理,经修补后原裂缝或缺失的表面应与周围地面匹配. 表5 不同任务规模条件下的算法对比结果 表6 不同AGV数量条件下的算法对比结果 从表5 和表6 的实验结果可知,与其他对比算法相较,IPSO算法无论是在不同任务规模条件下还是不同AGV 数量条件下的所有实验场景中得到的Fmin和Favg均优于其他对比算法,从中可以看出IPSO 算法具有较好的全局搜索能力,能搜索到质量较好的可行解。仿真结果表明了,在任务规模增大的情况下,IPSO算法仍具有良好的性能,能满足不同规模场景下的任务分配需求;除此之外,还能在任务规模一定,AGV 数量逐渐增加的情况下,算法仍保持良好的性能,求解出合理的任务分配方案。 本文对化肥站台堆区上多AGV 运载任务的调度问题进行了研究,首先,根据站台堆区现实环境设计化肥堆放方案,确定堆放布局并通过地图环境构建方法,然后,构建出化肥站台堆区环境模型,并结合企业实际需求,建立以运载任务总代价、运载任务工作量均衡为双重优化目标的数学模型,最后,提出基于混合策略改进粒子群算法为各AGV 合理分配任务。实验结果表明,相比GA、PSO、MPSO、PHSPSO 和SLPSO等算法,IPSO 算法无论是在不同任务规模条件下,还是不同AGV 数量条件下的所有实验场景中,得到的Fmin 和Favg均优于其他对比算法,验证了所提方法的可行性和优越性。2.2 基于Circle混沌反向学习的种群初始化策略
2.3 权重自适应非线性更新策略
2.4 基于差分学习的粒子变异策略
2.5 IPSO求解多AGV任务分配问题的步骤
3 算例验证与结果分析



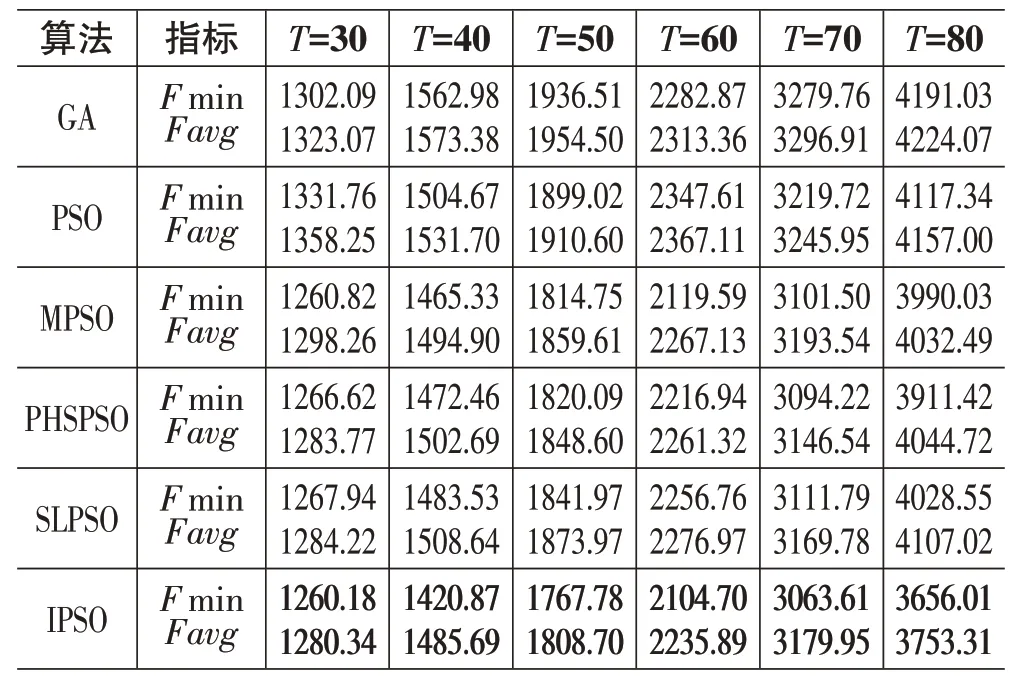

4 结束语

