基于等效平面法的切削仿真方法研究及优化*

陈树梁,徐 雷,任清川,牟宗亮

(四川大学机械工程学院,成都 610065)

0 引言

由于有限元仿真相比传统切削试验法成本低,而且能得到切削运动过程中更加直观地观察细节的变化规律,如材料的应变应力、刀具和切屑间接触应力、局部切削温度分布等,因此越来越多的国内外相关学者尝试运用有限元仿真来对金属铣削工艺和切削工艺过程进行研究[1]。对于常见侧铣和立铣,铣刀以侧边的周刃为主刃,端刃为副刃,当铣削过程中参与铣削工作的主刃长度远大于副刃时,则主刃参与主要的切削工作,便可以忽略副刃的作用,将铣削过程视为斜角切削[2],并且可以通过等效平面法,用二维正交切削仿真近似等效三维切削仿真来减少仿真时间。其中等效平面是指切屑在前刀面内速度方向与切削速度方向组合而成的平面,切削过程中材料的应变、剪切和切削流动都发生在等效平面内[3]。

但是目前,等效平面法的应用在铣削中的应用还不是很普遍,大部分学者还是基于主剖面而不是等效平面来进行斜角切削的二维仿真,导致仿真结果存在不小的误差。黄志刚、OZEL等[4-5]基于刀具主剖面建立了高硬度模具钢得二维切削有限元模型,分析了铣削加工过程中刀具温度的分布情况和铣削力的变化规律。也有一些学者采用了等效平面法,但是对等效平面法的应用还不是很完善。LI等[6]基于等效平面法得到刀具等效前角并构建了二维切削仿真模型,但并未对刀具其他参数进行等效处理。STEPHENSON等[7]基于等效平面法,对刀具的前角、后角和圆角多个参数进行了等效处理并建立了二维仿真模型,但并未对工件的参数进行等效处理。另外前面的研究中刀具参数大都是基于法剖面测量的,而实际上标准铣刀的给定的刀具参数是主剖面(正交平面)的参数。

针对以上问题,本文基于等效平面法,建立了主剖面内刀具参数和等效平面内刀具参数之间的转换模型,同时优化了等效平面法,除了对刀具参数进行等效处理外,也对工件的许多参数也进行了相应的等效处理。并建立了三维斜角切削仿真模型、基于优化的等效平面法的二维正交仿真模型以及基于优化之前的等效平面法的二维正交仿真模型3种仿真模型。并对3种模型的仿真结果进行了对比验证。

1 等效参数的推导

1.1 三维斜角切削几何模型

斜角切削与正交切削的区别在于斜角切削过程中切削刃与切削速度方向不垂直,即刃倾角λs≠0,这也导致把切屑流向与切削刃法线方向不一致,而两个方向的夹角称作流屑角ηc,影响流屑角的不确定因素很多,很难准确确定其值[8]。Stabler实验法则认为:在λs≤45°的情况下,流屑角几乎不受切削速度、前角、工件材料和刀具材料的影响,而是基本上等于刀具的刃倾角[8]。而本文仿真模型的刃倾角为30°,因此后面以ηc=30°进行计算。三维斜角切削的几何模型[9]如图1所示。

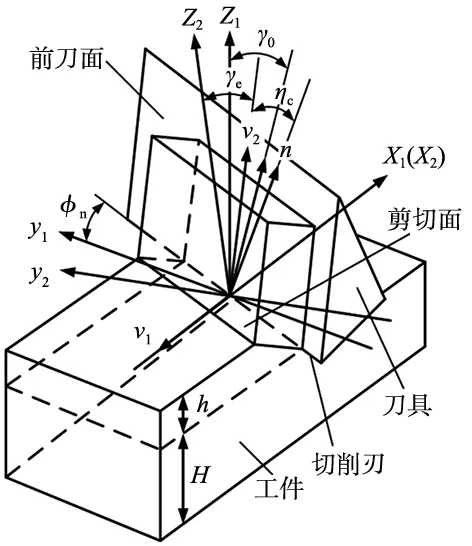
图1 三维斜角切削几何模型图

图中ηc为流屑角;Φn为铣刀的螺旋角,相当于斜角切削模型中的刃倾角λs;前角γ0为主剖面内测得的刀具前角,等效前角γe即为等效平面内测得的刀具前角。

1.2 刀具等效参数推导

1.2.1 刀具等效前角

为了求解刀具等效前角和等效后角,在坐标系O-X1Y1Z1中建立了前刀面和后刀面在主剖面和等效平面内的几何关系,其几何关系如图2所示。

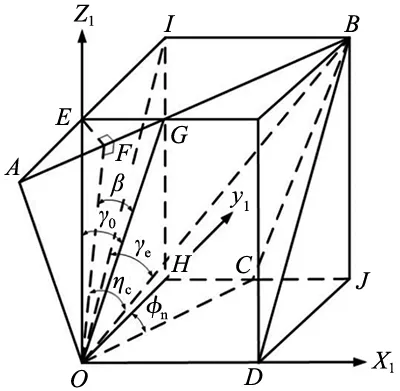
图2 斜角切削前刀面几何关系示意图

图中OC为切削刃其中一段;XOZ平面为主剖面(正交平面);YOZ平面为基面;XOZ平面为切削平面;OABC平面为前刀面;OB为切屑流出方向;OIBD平面为等效平面。

过E点做EF垂直AB,因为OE垂直AB,所以AB垂直OEF平面,即AB垂直OF,且∠FEG=Φn根据FG=EG·sinΦn可得:

sinβ=sinΦnsinγ0

(1)

求得β之后,可以推导出OC,BC的长度:

OC=BF-FG=OB·(sinηc-cosηctanβ)

(2)

(3)

根据OC,BC的长度可以进一步求得HC和CJ的长度:

HC=OC·sinΦn=OB·(sinηc-cosηctanβ)sinΦn

(4)

(5)

然后根据式(2)～式(5)可以推导出等效前角γe的关系式:

(6)

1.2.2 刀具等效后角

同理,求等效后角只需将图2中的前刀面看成后刀面即可,则由式(6)求出的为等效后角的余角。令α0为后角,αe为等效后角,则:

(7)

1.3 工件等效参数推导

1.3.1 等效切削厚度

如图2所示,根据式(2)和式(3)求出的OC,BC可以推导出EI,OE:

EI=OC·cosΦn

(8)

OE=BC·cosγ0

(9)

根据EI,EA可以得到∠IAE和∠LDM,即等效平面与正交平面的夹角(两平面交线方向与切削速度方向平行),令其为θ,则:

(10)

等效切削厚度he为切削厚度h在等效平面内的投影厚度,因此可以求得二维正交仿真模型的等效切削厚度:

(11)

1.3.2 等效基体厚度和等效比热

前面基于等效平面法求解了二维正交仿真的刀具等效参数和工件等效切削厚度,对于工件基体部分,二维正交仿真同样需要转换成等效平面内的参数。对于切削仿真,需要获取的主要结果主要是力和热。力是失量,有方向,且基体应力场分布主要受切削层应力场影响,而切屑流出方向在等效平面内,因此以等效平面内的等效基体厚度He来建立二维正交切削仿真,基体的应力场仿真结果会更接近三维切削仿真。与等效切削厚度类似,等效基体厚度He和实际基体厚度H的关系如下:

(12)

而热是一种能量场,其本质就是大量微观粒子运动的宏观表现,热的传导是由于物体内部或物体之间的温度差引起的[10]。因此工件的热传递会沿着工件材料形状传播,因此以正交平面内的实际基体厚度进行二维正交仿真能得到更精确的基体温度场。另外基体产生的应变几乎都是弹性应变,不会生热,即应力场分布不会影响温度场分布,但是温度场是会影响应力场,而以等效平面建立的二维正交切削仿真的基体等效厚度与实际基体厚度不等,所以得到的基体温度场与实际温度场不符,会导致基体应力场结果与实际不符。实际上基体的温度场分布随着切削进行处于一个近似动态平衡的状态,所以以等效平面建立的二维正交切削仿真得到的基体温度场与实际基体温度场整体分布是一致的,只是基体等效厚度为实际基体厚度的cosθ倍,而传导到基体的热量是一定的,导致单位体积获得的热量减少,使得仿真得到的基体温度比实际温度低,且比热和温升的关系为:

(13)

为了解决这个问题,不妨设工件基体部分的材料比热为等效比热ce,令等效比热为实际比热的cosθ倍,即:

ce=c·cosθ

(14)

这样同样的热量导致的温升可以提高cosθ倍,可以抵消体积变化带来的影响。因此通过使用等效基体厚度和等效比热建立的二维正交切削仿真对工件基体部分的应力和温度都能做到较好的预测。

1.3.3 等效摩擦系数

根据等效平面法的原理,两种模型在等效平面内的的主切削力是相等的,因此两种模型接触面的正压力大小是不同的,并且根据两种模型的几何关系可以得到两种模型接触面的正压力与主切削力关系:

Fn=[-1 tanΦntanγ0]·Fx

(15)

Fne=[-1 0 tanγe]·Fx

(16)

式中:Fn、Fne分别为三维斜角模型和二维正交模型的正压力,Fx为主切削力。

而两种模型的切削速度相同,因此会导致两种模型摩擦力做工(生热)不同,为了解决这个问题,不妨将二维正交切削模型接触面摩擦系数设置为等效摩擦系数μe,令:

(17)

这样就能使二维正交切削模型接触面的摩擦力和温度与三维斜角模型相符。

2 切削有限元模型

2.1 几何模型及边界条件

为了验证基于等效平面法用二维正交切削模型等效三维斜角切削模型的可行性和准确性,分别建立了三维斜角切削模型和二维正交切削模型,其中三维斜角切削模型中的刀具参数设置为:前角16°,后角16°,螺旋角为30°。二维正交切削模型中的刀具参数设置为其在等效平面内的参数,根据式(6)和式(7)计算得到刀具的等效前角为25.52°,等效后角为16.13°。

对于切削参数和工件参数,三维斜角切削模型的切削厚度h为0.03 mm,基体厚度H为0.17 mm,切削宽度b为0.6 mm,接触面的摩擦系数μ为0.3,根据式(10)计算得到θ=21.356 6°,由此进一步得到二维正交切削模型的等效切削厚度he为0.032 2 mm,等效基体厚度He为0.182 5 mm,接触面的等效摩擦系数为0.322,另外因为工件材料的比热随温度变化,工件材料的等效比热ce为相应温度下比热c的0.93倍。两个模型的切削速度都为3.351 m/s。

三维斜角切削仿真模型和二维正交切削仿真模型分别如图3和图4所示,图3中x轴为切削速度方向,切削刃与XOY平面平行,且与Y轴成30°夹角,即刃倾角。工件模型设计成与刀具契合的形状而不是长方体,这样可以使仿真更快进入稳定切削状态,节省仿真时间。工件模型中工件基体外表面部分设置边界条件为完全固定,刀具设为刚体。为了保证两种模型结果的准确性,刀具和工件采用一样的网格密度和分布。

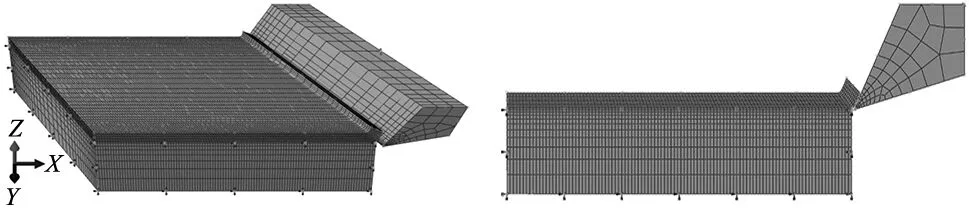
图3 三维斜角切削仿真模型 图4 二维正交切削仿真模型

2.2 工件材料本构模型

本文模型的工件采用7075铝合金材料,因为J-C本构模型能够较好地满足7075铝合金材料在铣削加工过程中的参数变化,以及很好地反映其高应变率情况下的力学特性[11]。因此采用J-C本构模型进行仿真,其本构方程如下[12]:

(18)

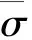
表1 7075铝合金的J-C本构模型参数

3 切削仿真结果对比分析

3.1 三维斜角切削仿真结果分析

首先验证二维正交切削模型是否能够代替三维斜角切削模型,三维斜角切削仿真的应力和温度结果分别如图5和图6所示。

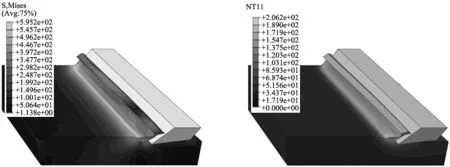
图5 三维斜角切削仿真应力分布图 图6 三维斜角切削仿真温度分布图

从图中可以看出,除了切削层两端面附近,三维斜角切削模型的应力和温度分布等值线基本与切削刃平行,这是因为切削层两端面附近的受力和变形情况不同于其他地方,但是相对于整个切削宽度这只是较小的一部分,因此用二维正交切削模型代替三维斜角切削模型进行仿真是可行的。

3.2 二维正交切削仿真结果分析与对比

为了比较使用等效摩擦力和等效比热的效果,再建立一个二维正交切削模型,该模型使用实际摩擦力和实际比热。然后取三维斜角切削模型中间的一个等效平面的温度场结果与两个二维正交切削模型的仿真结果进行对比,3种模型温度稳定后的同一时间、同一位置的温度场结果分别如图7所示。

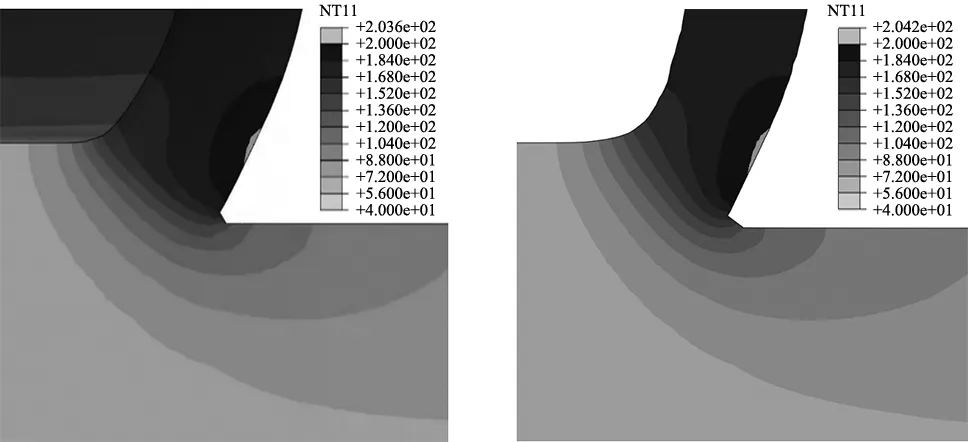
(a) 三维斜角切削(b) 优化的二维正交切削

首先将3个模型温度场稳定后的同一切削时间接触面的最高温度进行对比,结果如表2所示,从表中看出使用等效摩擦力参数之后,使得接触面的最高温度的误差有效减小,从9.63%降低到了0.29%,结果更加精确。

表2 接触面最高温度对比表

然后对3个模型的基体温度分布进行对比,从图中看出使用等效比热的基体温度场分布与三维斜角切削模型结果基本吻合,而使用实际比热的基体温度场与三维斜角切削模型结果存在明显的差异。因此可以认为使用等效摩擦力和等效比热建立的二维正交切削模型能有效减小仿真的温度场误差。

4 结论

(1)当切削宽度相比于切削厚度足够大时,基于等效平面法建立的二维正交切削模型仿真结果与斜角切削模型仿真结果相近;

(2)基于优化的等效平面法建立的二维正交切削模

型有效地减少了仿真的误差。其中刀具与工件接触区域的最大温度误差从9.63%降低到了0.29%,另外工件基体的温度分布也得到明显改善,与三维模型温度分布基本吻合。