正五边形-椭圆形复合微孔化机械密封性能研究*

杨天佑,穆塔里夫·阿赫迈德,b,王禹辉

(新疆大学a.机械工程学院;b.电气工程学院,乌鲁木齐 830047)

0 引言

微孔机械密封是近年来润滑与密封领域的研究热点之一[1]。彭旭东等[2]的研究指出椭圆微孔排布会对泄漏率产生影响;石卓等[3]关于椭圆微孔在微孔深度等对液膜承载力的影响;张科等[4]的研究指出在不同参数下关于方向角影响泄漏率的研究,几何收敛点会随着方向角的改变而发生改变;谢静、白少先等[5-6]的研究指出倾斜的椭圆微孔会产生上游泵送特性,通过改变参数可实现零泄露;吉华等[7]的研究表明倾斜椭圆孔会产生回吸,进而降低泄漏量;战琳月等[8]对其考虑椭圆微孔的方向角进行的不同排布,得到不同排布下泄漏量和开启力,根据所需工况选取不同的排布。吉华等[9]的指出等边三角形微孔的会产生多楔现象,泄漏率和开启力取最小值,所对应方向角不同;陈胡炜等[10]提出一种新的微孔,具有泄露量小的性能;章亦聪等[11]提出了一种莱洛三角形微孔;程香平等[12]的研究表明双向菱形孔有较好的密封特性;阮鸿雁等[13]提出三角形和多圆弧复合织构,该织构具有良好的流体动压润滑性能;魏伟等[14-15]的研究指出复合织构和复合槽孔织构具有较好的密封性能。

目前,对于复合微孔化织构机械密封的研究较少。因此,本次研究从正五边形-椭圆形复合微孔机械密封端面出发,建立了正五边形-椭圆复合微孔机械密封理论模型。分析不同参数对承载力和泄漏量的影响,对其微孔进行比较,得到复合微孔密封端面较大的承载力和较小的泄漏量。

1 理论模型

1.1 几何模型

微孔机械密封的密封环截面几何结构如图1所示,机械密封摩擦副由动、静环以及流体膜,内径为rin,外径为rout,旋转速度为n,微孔深度为hp,密封端面间隙为ho。

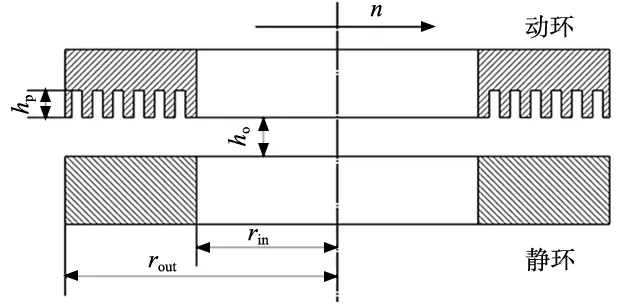
图1 微孔机械密封的密封环截面结构示意图

在动环上进行开孔,动环开微孔如图2所示。微孔沿径向逐个排布,微孔沿轴向周期对称,提高计算效率,选取动环的1/36。

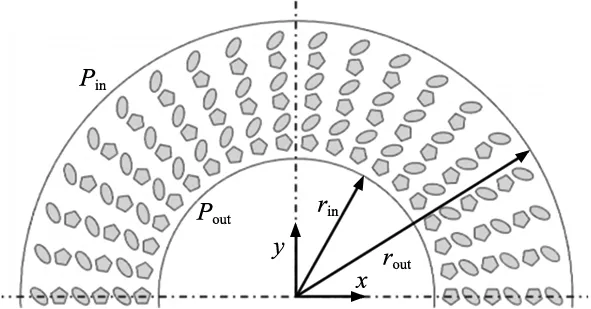
图2 动环复合表面微孔

1.2 数学模型

通过简化的雷诺方程为:

(1)

流体的局部膜厚为:

(2)

式中:A1为无微孔区域,A2为有微孔区域。

施加强制边界条件,压力边界条件为:

(3)

周期性边界条件为:

(4)

式中:θ1、θ2表示开微孔的流体膜模型在圆周方向的起始角度和终止角度。

联立式(1) ～式(4)可以得到简化计算的流体膜的泄漏量Q、承载力F以及开漏比I:

F=∬pdA

(5)

(6)

(7)

1.3 网格划分与网格无关性验证

采用mesh模块对微孔液膜模型进行网格划分。选取如下:面积率Sp=10%,密封端面间隙ho=2 μm,微孔深度hp=3 μm,旋转速度n=6000 r/min,压力进口pi=0.2 MPa,压力出口po=0.1 MPa,网格质量对计算结果影响,随着网格数量的逐渐增加,承载力的逐渐增大,直至稳定2.62 N附近,其网格数量为1 903 773,节点数3 627 626,网格质量平均质量为0.91,其网格质量较高,因而选取网格数量为1 903 773个,见图3。

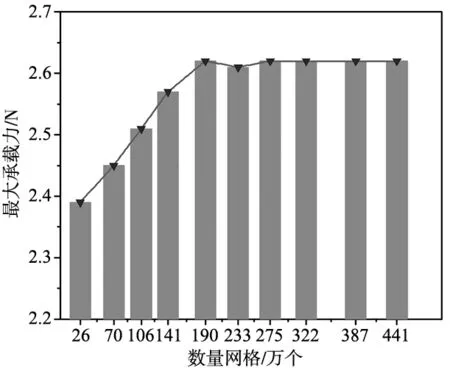
图3 网格数量对计算结果的影响

2 计算结果与分析

2.1 流体膜压力分布

内径rin=15 mm,外径rout=20 mm,在面积率Sp=10%,密封端面间隙ho=2 μm,微孔深度hp=3 μm,旋转速度n=7000 r/min,压力进口pi=0.2 MPa,压力出口po=0.1 MPa,流体介质为清水,其温度为20 ℃,密度ρ=998.2 kg/m3,粘度μ=1.003 mPa/s。则得到正五边形微孔、椭圆形微孔和复合微孔的流体膜压力分布如图4所示。

(a) 正五边形密封端面 (b) 椭圆形微孔密封端面

由图4可知,流体压力沿周向成周期性分布,沿径向从外向内逐渐减小。密封环外径处线速度大,因此外侧流体可获得较大的动能和压力。不同的复合微孔间相互影响,使得复合微孔的动压效应更强,微孔处的压力峰值更高,使得流体膜的最大压力变大。

2.2 微孔深度对密封性能的影响

图5在面积率Sp=10%,密封端面间隙ho=2 μm,微孔深度hp=1～7 μm,旋转速度n=5000 r/min,压力进口pi=0.2 MPa,压力出口po=0.1 MPa下得到不同微孔的泄漏量Q、承载力F以及开漏比I的变化曲线。

(a) 对泄漏量Q的影响 (b) 对承载力F的影响

由图5a可以看出,当微孔深度hp=3 μm左右时,单一微孔和复合微孔的泄漏量取得了最大值,微孔深度在1～7 μm范围内,单一微孔和复合微孔的泄漏量随微孔深度的增大而先增加后减少,且单一微孔和复合微孔的泄漏量的变化规律均相同。同时,当在同一微孔深度的情况下,泄漏量由小到大依次为复合微孔、椭圆形微孔和正五边形微孔。由图5b可以看出,当微孔深度hp=3 μm左右时,单一微孔和复合微孔的承载力取得了最大值,微孔深度在1～7 μm范围内,单一微孔和复合微孔的承载力随微孔深度的增大而先增加后减少,且单一微孔和复合微孔的承载力的变化规律均相同。同时,当在同一微孔深度的情况下,承载力由小到大依次为正五边形微孔、椭圆形微孔和复合微孔。由图5c可以看出,当微孔深度hp=3 μm左右时,单一微孔和复合微孔的漏比取得最小值,微孔深度在1～7 μm范围内,单一微孔和复合微孔的开漏比均随微孔深度的增大而先减小后增大,且单一微孔和复合微孔的开漏比的变化规律均相同。同时,当在同一微孔深度的情况下,开漏比由小到大依次为正五边形微孔、椭圆形微孔和复合微孔。

2.3 面积比对密封性能的影响

图6在密封端面间隙ho=2 μm,微孔深度hp=3 μm,面积比Sp=6～24%,旋转速度n=7000 r/min,压力进口pi=0.2 MPa,压力出口po=0.1 MPa下得到不同微孔的泄漏量Q、承载力F以及开漏比I的变化曲线。

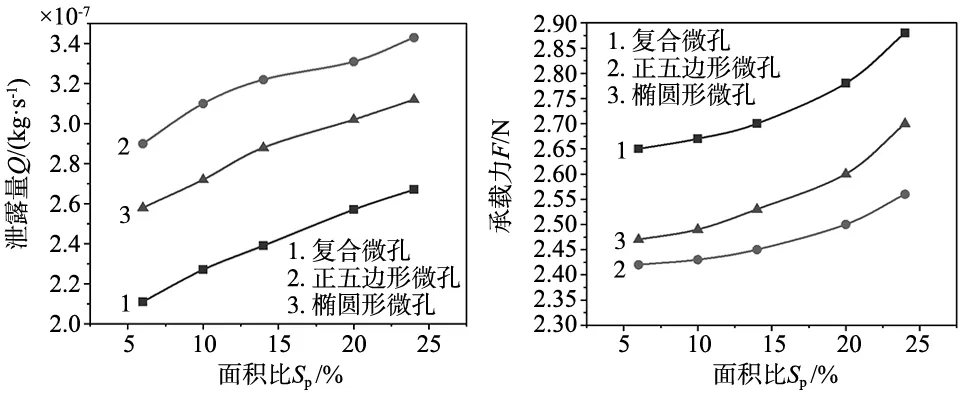
(a) 对泄漏量Q的影响 (b) 对承载力F的影响

从图6可以看出,当面积比在6%～24%范围内,单一微孔和复合微孔的泄漏量和承载力均随面积比的增大而升高,且单一微孔和复合微孔的泄漏量和承载力的变化规律均相同,其开漏比随面积比的增大而减小,且单一微孔和复合微孔的开漏比的变化规律均相同。同时,当在同一面积比的情况下,泄漏量由小到大依次为复合微孔、椭圆形微孔和正五边形微孔,承载力和开漏比由小到大依次为正五边形微孔、椭圆形微孔和复合微孔。

2.4 速度对密封性能的影响

图7在面积率Sp=10%,密封端面间隙ho=2 μm,微孔深度hp=3 μm,旋转速度n=2000～8000 r/min,压力进口pi=0.2 MPa,压力出口po=0.1 MPa下得到不同微孔的泄漏量Q、承载力F以及开漏比I的变化曲线。

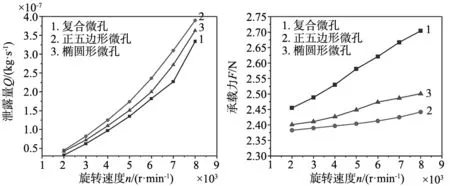
(a) 对泄漏量Q的影响 (b) 对承载力F的影响

由图7a可以看出,当旋转速度在2000～8000 r/min范围内,不同微孔的泄漏量均随旋转速度的增大而升高,不同微孔泄漏量变化规律均相同。同时,在同一旋转速度的情况下,泄漏量由小到大依次为复合微孔、椭圆形微孔和正五边形微孔。由图7b可以看出,当旋转速度在2000～8000 r/min范围内,不同微孔的承载力均随旋转速度的增大而升高,复合微孔的承载力上升趋势明显,而单一微孔的承载力上升趋势平缓。不同微孔承载力变化规律均接近于线性变化。同时,在同一旋转速度的情况下,承载力由小到大依次为正五边形微孔、椭圆形微孔和复合微孔。旋转速度在2000～8000 r/min时,复合微孔的承载力增加了10.24%,复合微孔的变化率最大,椭圆形微的承载力增加了4.16%,正五边形微孔的承载力增加了2.48%。由图7c可以看出,当旋转速度在2000～8000 r/min范围内,不同微孔的开漏比均随旋转速度的增大而降低,不同微孔泄漏量变化规律均相同。同时,在同一旋转速度的情况下,开漏比由小到大依次为正五边形微孔、椭圆形微孔和复合微孔。

2.5 压力进口对密封性能的影响

图8在面积率Sp=10%,密封端面间隙ho=2 μm,微孔深度hp=3 μm,旋转速度n=7000 r/min,压力进口pi=0.2～0.7 MPa,压力出口po=0.1 MPa下得到不同微孔的泄漏量Q、承载力F以及开漏比I的变化曲线。

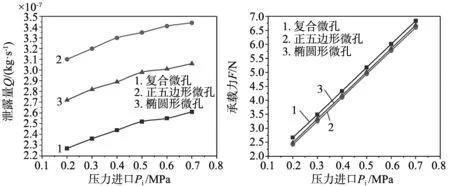
(a) 对泄漏量Q的影响 (b) 对承载力F的影响

由图8a可以看出,当压力进口在0.2～0.7 MPa范围内,不同微孔的泄漏量均随压力进口的增大而升高,不同微孔泄漏量变化规律均相同。同时,在同一压力进口的情况下,泄漏量由小到大依次为复合微孔、椭圆形微孔和正五边形微孔。由图8b可以看出,当压力进口在0.2～0.7 MPa范围内,不同微孔的承载力均随压力进口的增大而升高,不同微孔承载力变化规律均接近于线性变化。同时,在同一压力进口的情况下,承载力由小到大依次为正五边形微孔、椭圆形微孔和复合微孔。由图8c可以看出,当压力进口在0.2～0.7 MPa范围内,不同微孔的开漏比均随压力进口的增大而增加,不同微孔承载力变化规律均接近于线性变化。同时,在同一压力进口的情况下,开漏比由小到大依次为正五边形微孔、椭圆形微孔和复合微孔。

3 结论

(1)建立复合微孔流体膜的几何模型,通过对其进行数值模拟,对比其不同参数等对密封性能的影响规律。

(2)微孔深度3 μm左右时,单一微孔和复合微孔的泄漏量和承载力均取得了最大值,其开漏比取得了最小值。

(3)复合微孔化机械密封具有较大的承载力和较大的开漏比、较小的泄漏量,复合微孔化端面具有良好的密封性能。