基于视觉的轮毂磨抛初始点寻找与对准控制

戴伊宁，方灶军，潘 聪

1.宁波大学信息科学与工程学院，浙江宁波315211

2.中国科学院宁波材料技术与工程研究所，浙江宁波315201

3.浙江省机器人与智能制造装备技术重点实验室，浙江宁波315201

磨抛是影响轮毂外观和质量的重要因素。然而，目前轮毂磨抛主要以人工为主，磨抛效率低，无法保证磨抛质量一致，而且生产环境恶劣，工作强度大等问题严重影响工人的健康。所以，实现自动化磨抛逐渐成为该领域迫切解决的问题[1]。与人工磨抛相比，机器人磨抛具有磨抛效率高、精度高、质量好等特点。目前的机器人磨抛大多采取离线编程，事先设计好轮毂的磨抛轨迹，使其实现自动化磨抛。Tian 等[2]设计了一种基于六自由度工业机器人和六维力/力矩传感器的曲面机器人抛光系统。Kharidege 等[3]提出了一种自动抛光系统的方案，该系统包括一个六自由度臂机器人。描述了一种基于CAD 系统数据的自动规划和编程系统，用于创建机器人路径。Liu 等[4]结合机器人控制和轮式抛光技术的优点，建立了基于工业机器人的带缸轮式抛光结构。可灵活适应非球面的表面形状，同时基于抛光轮与工作表面的摩擦力，在精确压力的控制下获得高精度表面。

上述机器人磨抛系统只对机器人磨抛过程和磨抛轨迹进行研究，未对轮毂磨抛初始点对准问题进行研究。但是轮毂初始点对准是轮毂磨抛的重要环节，其定位的精度直接影响后续机器人的磨抛路径和最终的磨抛质量。虽然轮毂初始点定位的参考文献报道较少，但是有学者研究了基于视觉的焊缝初始点对准[5]。He等[6]提出一种提取焊缝轮廓特征点的方案，以实现自动多道次路径规划，并在MAG 电弧焊过程中指导各层的初始焊接位置的方法。Fan等[7]提出了一种基于激光视觉传感器的窄焊缝初始点对准方法。王小刚等[8]设计了一种由双摄像机组成的视觉采集系统，并提出一种熔滴—焊缝同步采集焊接偏差测定方法。但轮毂表面形状复杂，上述焊缝初始点对准方法不适用于轮毂初始点的对准。在轮毂初始点对准方面，Fang等[9]利用视觉传感器的非接触性和高精度的优点，提出了一种基于视觉的初始点对准控制方法，但该方法主要利用轮毂辐条信息。面对一些轮毂辐条形状复杂的轮毂，轮毂辐条的中心点往往较难提取。

针对轮毂初始点对准问题，提出了基于视觉的轮毂初始点对准方法，利用中心孔和螺栓孔计算角度偏差，并设计了基于模糊算法的轮毂初始点对准控制器，通过轮毂磨抛点对准实验验证了方法的有效性。

1 轮毂磨抛初始点对准系统

轮毂磨抛初始点对准系统如图1 所示。由于机器人抛光系统采用了机器人离线编程方法，因此只要轮毂类型不变，机器人抛光轨迹保持不变。一旦设定了磨抛目标初始点的位置，那么只要轮毂型号不变，目标初始点就保持不变。该系统由两个部分组成组成。第一个部分是视觉传感器部分，由一个工业相机和一个光源组成，由于轮毂具有一定的反射率，所以采用平行光源。通过工业相机拍摄得到轮毂图像，对轮毂图像进行图像处理和特征提取得到轮毂当前初始点相对于目标初始点的偏差角度，将得到的偏差角度传输给控制器。第二部分是控制部分，由控制系统和旋转台组成，控制系统接收视觉传感器计算的轮毂初始点角度偏差，通过控制算法计算出所需的控制指令，并发送给旋转台使得当前磨抛点对准到机器人磨抛的目标初始点，最后交给磨抛机器人进行磨抛。

图1 初始点对准系统示意图Fig.1 Schematic diagram of initial point alignment system

2 轮毂图像的预处理与特征提取

2.1 提取感兴趣区域（ROI）

在实际生产环境中，轮毂图片的背景比较杂乱，如图2（a）所示。利用掩膜（mask）和图像形态学技术提取感兴趣区域（ROI），可以有效地减少噪声干扰，利于特征的提取。轮毂是固定在旋转台上的，只会有旋转变换，不会有平移变换，所以轮毂的大致中心可以确定。而轮毂的螺栓孔分布在离轮毂中心r/2 左右（其中r 为轮毂的半径）。所以，将离圆心以r/2 为半径的圆内区域的图像作为ROI区域。详细操作如下：在图像中轮毂圆心位置，做一个半径为r/2 的掩膜和原图像做与（AND）操作。如式（1）所示：

图2 ROI提取结果Fig.2 Region of interest extraction

其中，Ir为最后提取到的感兴趣区域，Io为原轮毂图像，Im为掩膜。结果如图2所示。

图像二值化处理是预处理中的重要步骤，目的是使有用信息和无用信息的对比度达到最大，突出主题，方便后续提取。未经磨抛的轮毂其表面比较灰暗，其灰度值相较于螺栓孔而言会比较低，所以图像二值化可以较为完整地得到螺栓孔区域的图像。图像二值化可由公式（2）得到：

其中，I(x,y)是图像中像素点的灰度值，T 为灰度阈值，二值化实际就是用0或1来区分图像区域的过程。图像二值化的结果如图3所示。

图3 图像形态学操作Fig.3 Image morphology operations

在图像二值化之后还是会有一些亮点和噪点，这会对螺栓孔的边缘检测产生干扰。因此需除去这些亮斑和噪点。首先通过中值滤波[10]去除图像中的椒盐噪声，然后计算图像中各个连通区域的面积，通过设置连通区域面积的阈值大小，来去除亮点，保留所需要的螺栓孔信息。其公式如下：

式中，Sv为有效的连通区域的集合，Sk为第K个连通区域的集合。Ak为第K个连通区域的面积。AT为连通区域面积大小的阈值。

在得到大致的螺栓孔二值图像后，为了减少一些小孔洞对后续求螺栓孔边缘的影响，需要通过形态学的闭运算来去除小孔洞。

式中，Ab为螺栓孔二值图像，Bc为结构元素。即先对图像做结构元素为Bc的膨胀操作，再对图像做结构元为Bc的腐蚀操作。如图3所示。

2.2 边缘提取

为了实现对螺栓孔特征的提取，需要先对图片进行预处理，并且利用Canny算子对处理之后的图片进行边缘检测，得到含有螺栓孔目标边缘的图片。使用形态学边界提取来提取出螺栓孔边界。

式中，A为螺栓孔的二值图像，β(Ab)为图像Ab的边界，Be是适当的结构元素。

由于二值图像的边界是经过多次形态学操作后得到的，与实际的螺栓孔边界存在的偏差，所以需要将其当作掩码与原图做一次与（AND）操作，这样能得到准确的螺栓孔边界灰度图像。具体操作如下，对得到的二值图像的边界做膨胀操作，然后将其作为掩码与原图像做与操作（具体操作参考公式（1））。结果如图4（a）所示。

图4 利用Canny算子提取到的边缘Fig.4 Edges extracted by Canny operator

在对螺栓孔进行圆拟合来获取螺栓孔圆心位置信息前，直接对螺栓孔的灰度图像进行处理，会增加计算的时间，伴随的噪声会使得拟合圆的圆心与实际螺栓孔圆心偏差较大。所以，需对螺栓孔灰度图像的边缘进行检测，用螺栓孔的边缘信息来计算螺栓孔的圆心位置。

传统的Canny[11-12]算子通过用2×2 邻域的一阶偏导的有限差分来进行计算，在计算梯度幅值时对噪声比较敏感。因此为了提高检测的准确性，使用4个方向的梯度模板作为边缘检测梯度算子检测图像的边缘，计算像素的0°、45°、90°以及135°方向的梯度幅值，可以达到良好的边缘定位和噪声抑制的效果。如图4所示。

2.3 计算螺栓孔圆心

由于相机角度和轮毂表面反射光的问题，对图片处理后，螺栓孔边缘的图像可能呈现一种形变圆或者残缺圆的情况，成为计算螺栓孔圆心的干扰项，影响检测的准确度。如图5所示。

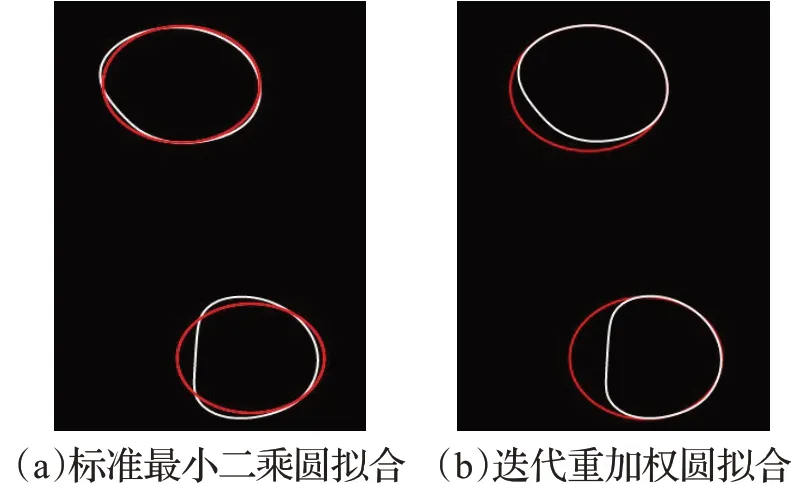
图5 拟合圆螺栓孔Fig.5 Fitting round bolt holes

图5（a）为使用最小二乘法拟合圆，图5（b）为使用迭代重加权最小二乘法拟合圆。实际上边界图像中凹陷的边缘一定是处于螺栓孔圆内部的，如果使用标准的最小二乘法拟合圆算法来拟合圆，结果容易受外点（凹陷边缘）的影响，使得最后拟合出的圆会比实际螺栓孔圆小，对应的圆心与实际圆心也会有些偏移。为了减少外点的影响，选用迭代重加权最小二乘法拟合圆算法[13-14]。该算法采用一个迭代过程求解一系列加权最小二乘问题，并在每一步迭代中按照一定的规则对权系数进行调整，使其逐步逼近最优拉格朗日乘子，使最小二乘解逐渐逼近最小区域解。具体拟合圆的原理如下。假设圆的方程为：

建立最小误差函数E：

其中，A=-2a,B=-2b,C=a2+b2-R2。样本点(xi,yi)到圆心的距离为di。

令(xi,yi)到圆边缘距离的平方与半径的平方差为：

为了减小离群点对拟合圆时的影响，引入权重函数ω：

其中，γ为削波因数，它定义哪些点为离群点。

迭代解得使得E最小的A,B,C值即为最终解。并确定圆和圆心的位置信息。

3 计算对准角度

轮毂的旋转角度由轮毂的中心和螺栓孔中心决定。因此计算出各个螺栓孔的中心后，需要计算轮毂的中心。通常为了轮毂的结构稳定，轮毂的螺栓孔是均匀分布在轮毂上，故所有螺栓孔中心会均匀落在以轮毂中心为圆心的圆上，通过取螺栓孔中心的平均值能较为精确地计算出轮毂的中心位置，公式如下：

其中，(xo,yo)为轮毂中心的横坐标与纵坐标，N为轮毂孔洞个数。(xhi,yhi)为第i个螺栓孔的中心横坐标与纵坐标。

根据轮毂中心和一个螺栓孔中心可以计算出与x轴正半轴相差的角度，但是由于光的反射和相机拍摄角度问题，拍出的图像会有些许的形变，计算螺栓孔中心时存在些许误差，精度无法得到保证，所以提出从总体上计算轮毂对准所需的角度。假设过轮毂中心和第i个螺栓孔中心的直线为：

其中，ai和bi为过轮毂中心和第i个螺栓孔中心的直线，n为螺栓孔个数。那么第i条直线到水平正半轴的夹角可以表示为：

由于螺栓孔是均匀分布的，如图6 所示。那么第i线到i+1 条直线所需要的旋转角度是一定的（其中i=1,2,…,n,n为螺栓孔个数），即螺栓孔是周期分布的。可求得一个周期为：

图6 轮毂中心和螺栓孔中心的连线Fig.6 Line connecting center of hub and bolt

其中，θc为相邻两条直线之间相差的旋转角度记为一个周期。那么可以利用螺栓孔周期分布的特性，将过轮毂中心和第i螺栓孔中心的直线与水平x正半轴之间的夹角θl变换到[0,θc]这个区间内，便于最终对准角度的选取。公式如下：

其中，θil是经过周期变换处理过后的角度，θi周期变换处理前的角度，mod为取余操作。

图像拍摄产生形变，图像处理、圆拟合等过程中会产生误差，故每个θ会存在些许偏差。为了减小误差，将所有的θil进行升序排列，然后取其中值的方法，来减小误差。公式如式（18）所示：

其中，θm为θil按序排列后取得的中值。机器人磨抛轮毂时，目标初始点是一定的。假设目标初始点与x轴正半轴的夹角为θt，同样的θt也需要进行周期处理，详细见公式（16）、（17）。那么可以得到当前初始点对准到目标初始点所需的旋转角度记为θr，那么可求得θr的公式如下：

电机既可以顺时针旋转，又可以逆时针旋转，所以在得到对准角度之后需判断对准角度是否大于1/2个螺栓孔分布周期，这样能让电机旋转最小的角度，减小旋转过程带来的误差。公式如下：

其中，θ′r为最终对准角度。得到对准所需旋转的角度后，将其交给控制器，由控制器控制旋转器实现轮毂磨抛初始点的校准。

4 初始点对准控制器的设计

采用开环控制方法无法保证初始点对准的精度，且初始点特征提取容易受到光照条件影响，难以建立磨抛初始点对准过程的数学模型。而模糊控制能解决无法建立精确数学模型系统的控制问题，且抗干扰性好，适应力强。因此提出了基于模糊控制[15]算法的初始点对准闭环控制算法，如图7所示。该控制器由两个通道组成，反馈通道和前向通道。反馈通道根据视觉传感器检测轮毂的当前初始点位置，并计算出的实际旋转角度。它由图像处理和角度计算两部分组成。前向通道根据轮毂当前磨抛点和目标初始点之间的误差，控制旋转器来调整轮毂旋转。为了确保对准精度，在初始点对准控制中采用模糊控制器，将理想旋转角度和实际旋转角度的差值E和E的变化量EC作为输入量输入模糊控制器，最后模糊控制器的输出量为脉冲数P。

图7 初始点对准控制示意图Fig.7 Schematic diagram of initial point alignment control

其中，θr是期望旋转的角度，θy是实际旋转的角度，E(k)是控制器第k次采样后的角度误差值。设E的基本论域为[-1°,1°],EC的基本论域为[-0.8°,0.8°],E和EC的模糊变量的为SE和SEC，建立定义SE和SEC的模糊子集各取5个语言值即{负大，负小，零，正小，正大}记为{NB，NS，ZO，PS，PB}。模糊控制最终的输出，即输入旋转器的脉冲数，定义其基本论域为[-420,420]。模糊子集为{负大，负小，零，正小，正大}，同样记为{NB，NS，ZO，PS，PB}。对于隶属度函数，输入量和输出量的隶属度函数如图8所示。选择的模糊推理方法是Mamdani法。模糊规则如表1所示。对于输出的模糊量，采用重心法解模糊化公式如下：

表1 模糊规则表Table 1 Fuzzy rule table

图8 输入输出的隶属度函数Fig.8 Membership function of input and output

式中，vi为第i个输出值。μ(vi)为输出变量的属度函数。

5 实验

为了验证基于视觉的轮毂初始对准控制方法的有效性，进行了大量实验。实验设备如下：主旋转器为Weiss CR0700C。旋转器由伺服电机驱动。视觉传感器由光源和数字工业摄像机组成。光源为FG-THZ338318，可发出定向光来减少拍摄环境的光线变化。相机的型号是MER-131-75GC，通过USB 端口连接电脑拍摄图像。相机得到的图像大小为1 024×1 080像素。图像处理使用C++、Opencv2。初始点对准控制器在永宏PLC 中实现。轮毂的视觉测量值通过计算机处理获得，然后通过RS232端口将数据从计算机端发送到PLC，最后由PLC控制伺服电机对轮毂初始点进行对准。处理一幅图像的时间约为75 ms。目标初始点和当前初始点的定义如下。目标初始点的位置需要人工设定，即最后交给磨抛机器人的初始磨抛位置。同一种型号的轮毂磨抛轨迹是相同的，所以同种型号轮毂的目标初始点也相同，只需人工设定一次即可。然后计算每个轮毂的当前初始位置。由于轮毂的当前初始点被用作闭环控制器中的反馈信号，因此在每个控制采样时间内计算它。

首先验证上述图像处理方法对不同型号轮毂的适用性。采取不同型号的轮毂使用上述的特征提取方法。图9 为对不同型号轮毂螺栓孔拟合的结果。再通过闭环控制实现磨抛初始点对准。其次对轮毂的对准精度进行了验证如图10~11所示。由图10可得，起始的对准误差为0.915 5 rad，在经过多次对准之后误差在0.1 rad 附近有个震荡，最后在第7 次对准后开始收敛。这里将停止对准的阈值设0.05 rad，即视觉部分计算出的初始点对准角度小于0.05 rad 时将其视为对准成功，结束对准控制。图11为每个对准周期经过模糊控制器后输入到PLC的脉冲值。

图9 不同轮毂型号拟合出的螺栓孔Fig.9 Bolt holes fitted with different wheel hub models

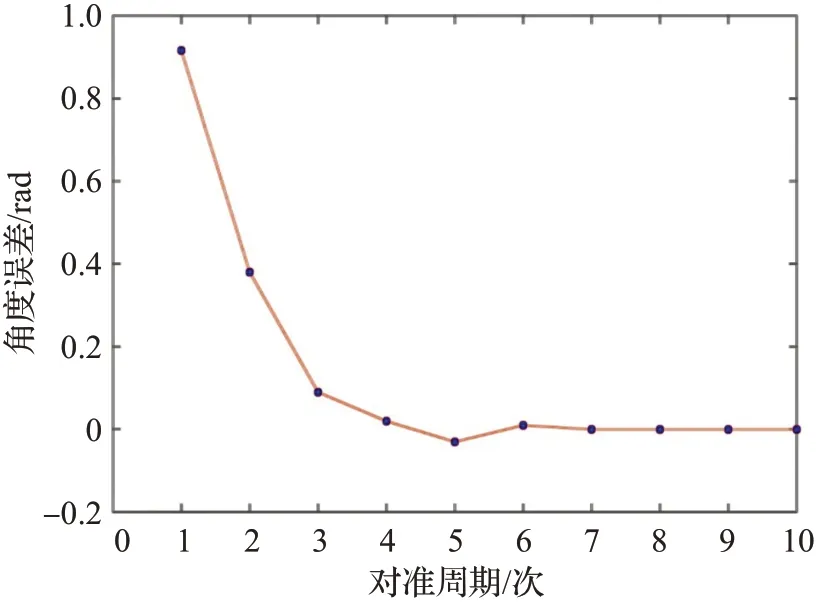
图10 角度误差Fig.10 Angle error

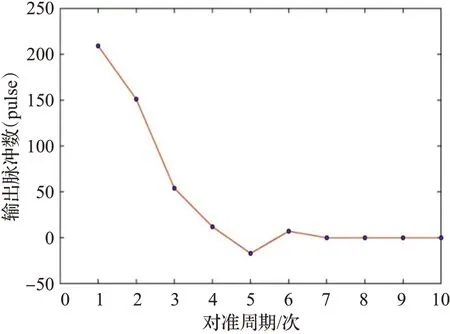
图11 输出脉冲数Fig.11 Number of output pulses

当对准结束后，用像素点的个数来计算对准误差，如图12所示。图12（a）将菲林尺置于轮毂侧面（菲林尺最小刻度为0.1 mm）通过测量得到1 mm大约为50个像素的长度。由图12（b）为目标位置，图12（c）对准完成后的位置，由图12 可以看到对准后菲林尺子位置与目标位置偏移了5个像素点。即对准误差大约在0.1 mm。

图12 对准误差Fig.12 Alignment error

初始点对准过程可见图13。为了方便呈现对准效果，图中用马克笔做的黑色竖线记号为当前磨抛初始点，而红色激光点为目标磨抛初始点。经过多次对准控制，黑色竖线逐渐靠近激光点，最终重合，即完成初始点定位。经过多次实验验证表明，如表2，上述轮毂初始点对准方法对于不同型号轮毂磨的定位精度皆控制在0.1 mm左右。

表2 各初始点对准算法适用性和精度对比Table 2 Comparison of applicability and accuracy of each initia point alignment algorithm

图13 磨抛点对准过程Fig.13 Grinding point alignment process

相较于文献[8]，本文将初始点对准运用在轮毂较磨抛上，将对准精度控制在0.1 mm左右，符合磨抛初始点的对准精度。相较于文献[9]，本文虽然在精度上没有什么提升，但是文献[9]适用的轮毂种类较少，面对轮辐复杂的轮毂，其定位效果并不太理想，且易受环境影响，而本文的方法适用于更多种类的轮毂磨抛初始点的对准。

6 结论

轮毂磨抛初始点的对准是机器人磨抛轮毂的重要过程，也是实现磨抛自动化的重要环节。然而传统的接触式传感器难以满足表面复杂轮毂的磨抛点的对准，为了高效、准确地对准初始点，使用了非接触式视觉传感器，并提出了一种基于视觉的初始点对准方法。轮毂当前初始点与目标初始点的差值表示为所需的轮毂旋转角度，可以通过轮毂螺栓孔中心和轮毂中性能计算得到。为此使用了基于迭代重加权最小二乘法拟合圆算法去拟合螺栓孔，并计算螺栓孔中心位置。在得到对准角度后，需要控制轮毂旋转，使得当前磨抛初始点对准到目标初始点，为此采用模糊控制，设计了一个初始点对准闭环控制系统。最后对几种不同型号的轮毂进行了对准实验，多次实验表明，本文提出的轮毂初始点对准算法可以将对准精度控制在小于0.1 mm，可以很好地满足轮毂磨抛机器人的需求。