改进的NSGA-III-XGBoost算法在股票预测中的应用

何 泳，李 环

东莞理工学院计算机科学与技术学院，广东东莞523000

股票预测是计算机科学与金融交叉的经典问题。新闻、政策、市场情绪等许多不确定因素都可能导致股票价格在短期内发生剧烈变化。股票的时间价格序列往往被认为是动态非参数的、混乱的、嘈杂的非线性序列[1]，因此，准确的预测股票市场价格的趋势，以最大化资本收益和最小化损失，给金融研究人员和投资者带来挑战。

传统的股票预测的方法可以分为三类：基本面分析、技术分析、传统统计分析，其中基本面分析和技术分析是对个股最常用两种的方法，用于分析和预测股票市场行为[2]。传统统计分析方法预测时涉及统计方法，例如自回归移动平均（ARMA）和指数平滑（ES）等[3]，将股票价格的变动视为时间序列的函数，并作为回归问题解决。然而由于股票价格变动的存在众多内部和外部因素且难以量化，处理海量复杂股票数据所需的工作量巨大，因此传统的非人工智能方法在股价趋势预测中往往不尽如人意[4]。近年来人工智能技术的不断发展和股票数据易获得的特点，越来越多机器学习和深度学习的模型用于预测股票[1]。由于机器学习模型具有更强大的大数据处理能力和学习能力，能够处理输入特征和预测目标之间的非线性关系，因此其预测能力通常比传统的基本面分析的方式的更强[5]。通过准确的股票价格方向变动预测，投资者可以把握买卖时机，从而战胜市场并获取利润[6]。

目前的研究中，基本的股票数据处理流程为：数据预处理、特征工程、模型训练、优化、预测和评估。然而，大部分的工作都集中在预测算法而忽视了特征工程。即使深度学习可以做到全自动的特征工程，也需要在输入模型之前进行数据预处理，好的特征工程可以使预测模型达到更好性能的同时减少运行资源[7]。因此，本文首先在特征工程方面进行数据降噪和生成技术指标，而后使用结合了多目标优化（NSGA-III）算法和机器学习算法（XGBoost）的股票预测模型进行特征选择并对股票的变动方向进行预测。

本文股票预测模型的优点如下：（1）高效。本文提出的算法与深度学习中长短时记忆神经网络（long short term memory neural network，LSTM）神经网络相比，在相同的优化次数下，准确度比后者高的同时，所需运行时间不到后者的1%。（2）可解释性。深度学习模型普遍存在“黑盒”问题[8]，无法对特征的重要性进行评估，而本文提出算法可以得出重要性最高的特征，以供后续研究。（3）高准确度和稳定性，本文算法与其他基准研究相比，体现了其预测能力和应对不同市场数据的预测稳定性。

1 相关工作

近几年，深度学习在图像识别、语音识别和自然语言处理等领域非常热门，其中也包括时间序列分析。在时间序列分析中，LSTM由于其特殊的门结构，可以记忆过去一段长度的输入并解决了循环神经网络（recurrent neural network，RNN）中的梯度消失问题，成为研究的热门。其中文献[9]使用遗传算法将均方根误差（RMSE）作为适应度函数，优化了神经网络。文献[10]采用数据增强的方式，并用一个预测LSTM 和一个防止过拟合LSTM 来提高预测性能。文献[11]提出一个复合模型，LSTM结合了经验小波分解和异常值鲁棒极端学习机。除了深度学习多种机器学习模型也用来开发股票预测系统。例如文献[12]使用基于树的集成学习方式，文献[6]使用遗传算法优化的XGBoost，文献[13]采用非线性高斯核函数的权重支持向量机（support vector machine，SVM）进行特征工程，并用权重K邻近算法预测价格。

特征工程是AI 技术的重要组成，许多研究在这一部分改进来提高模型的预测性能。文献[14]、文献[9]和文献[12]在原始的历史数据上生成技术指标来预测价格。而文献[12]在拓展特征后，采用特征提取的方式获得新的指标。然而，过多的特征输入不一定能提高模型的性能，反而可能导致“维度诅咒”的问题，造成不必要的计算消耗和模型预测能力的下降[15]。

基于以上研究的启发，本文提出的算法在拓展特征后，采用特征选择的方式，去除不相关的和冗余的特征，减少不必要计算开销的同时提高模型的预测性能。进化算法通过启发式搜索策略获得最佳特征子集，因为其高效的全局搜索方式被广泛应用于特征选择问题。目前大多数研究采用单目标的方式优化分类精度或分类误差来解决特征选择的问题，而该问题可以作为最大化预测性能和最小化特征数量的多目标问题。在实际应用中，如果能选择较小的解集并保持较高的预测性能，那么就能减少计算量的同时提高预测性能。因此，本文的预测系统可以看成多目标特征选择问题，用多目标算法解决。

2 方法与模型

为了解决高维数据的处理问题，本文通过特征选择方式移除与目标相关性低的特征和冗余的特征，从而提高计算效率和模型性能。本文提出INSGA-III-XGBoost算法使用多目标算法进行同步特征选择和参数优化，选择的特征子集和参数输入XGBoost 模型进行训练预测。在本文的研究中将选择的特征数和分类的准确度作为两个目标。其中，选择特征数量，即解大小的目标函数表示为：

分类准确度的计算公式为：

式中，Z为解码方案，D为维度（特征的个数），每个维度的可能值为0 和1，式（2）中，NCar为正确预测的样本数，NAll是所有样本的数量。

如图1 所示，本文采用多染色体混合编码的方式，第一条染色体编码了所有特征，染色体的长度等于数据的特征数量，其中0代表未选择该特征，1代表选择该特征将被保留。第二条染色体编码了XGBoost 的关键参数。图3 中的E为XGBoost 树的数量，F为XGBoost最大特征数，L为XGBoost学习率。

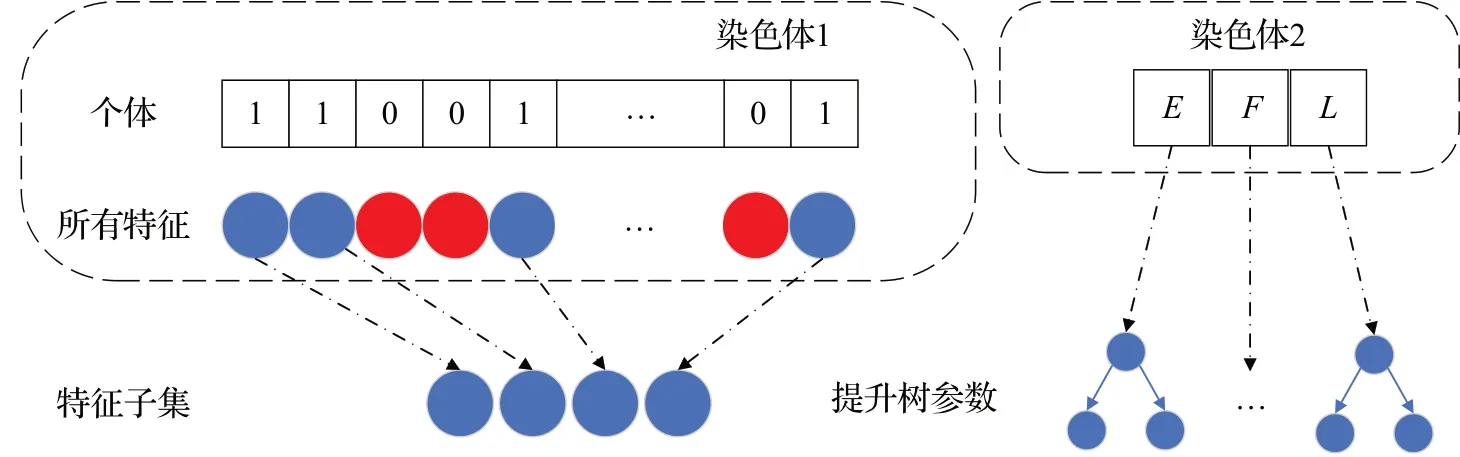
图1 个体表示Fig.1 Presentation of individual

卡方检验方法（Chi2）可以对特征进行相关性分析，因此在NSGA-III 算法的初始化阶段，可以用Chi2 先评估特征，在所有的特征变量里提取出与目标更相关的特征，并减少相关度低的冗余特征，用于初始化种群以提高性能。公式如下：

其中，实际值指变量x的实际频数，理论值指假设变量x与目标变量y之间独立时，x的理论频数。先通过Chi2 评估特征，获得每个特征变量对目标变量的卡方值，然后根据大小排序，选择排名靠前的特征，即是与目标变量y更相关的特征[16]。通常在Chi2 算法初始化过程中，需要保留大部分的评分较高的特征和不相关的特征的小部分以保持初始化的多样性（考虑特征之间的相互作用）。因此，通过实验对比，本文选择80%最有用的特征。而如何从选择的特征中得到最合适的特征组合，并且确定合适的特征数量又是需要考虑的问题。在本文中，采用混合初始化[17]的方法解决该问题：首先基于卡方值排序，从初始特征中选择得分最高的80%的特征保存在WR中，对于所有个体中的80%的个体，若个体选择的特征在WR且初始矩阵XG中选择了该特征（对应的值为1），则保留该特征。对于所有个体中的20%的个体，若个体选择的特征不在WR且初始矩阵XG选择了该特征，则保留该特征。

算法1 混合初始化

种群大小ps，特征数D，初始矩阵XG，前80%特征矩阵WR，记录矩阵PF

XGBoost 创建后每个属性的重要性得分可以直接获得，该得分衡量特征在提升树构建时的重要程度。在单个决策树，每棵树根据特征对性能度量改进的量计算属性重要性。在提升树中，单个特征对性能改进的程度越大，权值越大，并将被更多提升树所选择，重要性越高。最后根据属性在所有提升树中的重要性加权求和并平均，得到最终的重要性评分。由于其与Chi2 的评估方法不同，因此会得到不同的评估结果。基于Chi2和XGBoost的集成学习种群初始化过程如下：第一部分种群使用Chi2 评估特征的卡方值，根据其大小将特征从大到小排列，然后由算法1得到初始种群a，再将种群a作为XGBoost的输入，使用TPE（tree-structured parzen estimator）算法[18]优化50 次参数，得到原种群和准确度合并的新种群A。第二部分种群根据XGBoost 评估特征的重要性得分，根据重要性得分将特征从大到小排列，再由算法1 得到初始种群b，再将种群b作为XGBoost的输入，并使用TPE算法优化50次参数，得到原种群和准确度合并的新种群B。最后将新种群A和B合并，根据准确度排序，选择前50%的个体作为最终的初始化种群P。

NSGA-III在本文中用于解决多目标特征选择问题。NSGA-III[19]源自NSGA-II[20]，其框架类似于NSGA-II，但对选择运算符进行了重大更改。在NSGA-III 算法中，有一个广泛分布在整个归一化超平面上的一组参考点，保持种群的多样性。因此该算法很可能找到一个对应于这些参考点接近帕累托最优解的支配解集。而本文提出的INSGA-III-XGBoost算法通过收集并更新每代中达到的最高准确度的解集信息，搜索近似最优或最优解。图2展示了上述INSGA-III-XGBoost的过程。NSGA-III算法中某一代种群中所有个体将XGBoost 训练评估的适应度，经过选择、交叉、变异并不断迭代，找到最优解。XGBoost全称极端梯度提升树，它是在数据科学竞赛中占据主导地位的非深度学习算法，由陈天奇博士[21]设计开发，XGBoost 的优势在于其在所有场景中的可扩展性和极高的准确性。XGBoost 的可扩展性是由于算法采用加权分位数草图程序来处理具有并行和分布式计算的近似树学习中的实例权重。通过将可扩展性程序与梯度提升算法相结合，XGBoost可以通过利用每一个可用的硬件资源来最大化预测性能和处理速度。模型设计只关注性能和效率，能够并行地将多个弱分类器（决策树）通过结果加权的方式合成强分类器（提升树），是工程领域最好用的算法之一。

图2 INSGA-III-XGBoost算法Fig.2 INSGA-III-XGBoost algorithm

然而即使XGBoost在机器学习算法中取得了成功和实际普及，但很少有研究将XGBoost方法用于股市预测[22]。

3 实验结果与讨论

本文所有的实验均在如下配置的计算机中运行。硬件信息：英特尔i5-9500（3.00 GHz）处理器、8 GB RAM；软件信息：Python 3.8.5、Visual Studio Code 1.67.1、Jupyter notebook 6.4.6。因为市场状态可能潜在地影响股票预测的效果，因此从不同发展程度的市场选择指数有助于解释算法的鲁棒性。本文选择的3 只市场指数，道琼斯指数代表最发达市场指数，恒生指数代表比较发达市场的指数，沪深300 代表发展中市场的指数，所有数据均通过英为财情网（https：//cn.investing.com/）下载。数据样本的时间段为2008年7月1日至2016年9月30日。

3.1 数据降噪

小波变化具有处理不平稳的金融时间序列的能力，因此本文中使用了小波变化进行数据降噪。小波变换的关键特性是与傅里叶变换相比，它可以同时分析金融时间序列的频率分量。因此它可以有效地处理高度不规则的金融时间序列[23]。本文使用三层sys8 小波将指数价格序列分解为时域和频域。

3.2 生成技术指标

本文将建立两个指标集。一个是在前人的研究中常用的指标，一个是本文生成的指标，两个指标集进行对比。表1展示了前人研究中常用技术指标。

表1 技术指标集Table 1 Technical indicator set

表2 分类指标对比Table 2 Comparison of classification metrics

原始的历史数据只包括开盘价、收盘价、最高价、最低价和成交量。本文通过生成技术指标的方式，将初始的5 维数据拓展为81 维数据。所有的技术指标均通过TA-Lib库生成，可以分为六组，分别是重叠指标、动量指标、成交量指标、波动率指标、价格转换指标和循环指标。

3.3 数据清洗和归一化

将1 950个交易日的数据集划分，其中训练集85%、测试集15%。训练集分为前82%训练模型，后18%用来验证模型。公式（4）将数据集映射到[0，1]之间进行归一化。

3.4 性能衡量指标

实验采用下列的常用分类指标衡量算法性能。

其中，TP为真正率，TN为真负率，FP为假正率，FN为假负率。

3.5 单目标、多目标、改进多目标对比

3.5.1 分类指标

分别采用基于单目标的方法GA 和基于多目标的方法NSGA-III，以及基于改进后的多目标的方法INSGAIII结合XGBoost对三个数据集进行实验，比较不同特征选择算法的性能。采用的参数设置如下：进化代数200代，种群大小20，个体染色体数2，交叉率1，变异率0.05。实验数据如表3所示。表中可以看出在三个数据集中，INSGA-III-XGBoost算法在准确度、F1-score、AUC上均取到两个最佳，两个多目标算法选择的特征数均比单目标算法选择的特征较少。实验结果表明，从分类指标评价的角度上看，单纯把单目标特征选择问题转换为多目标特征选择问题效果不一定会更好，而本文改进INSGAIII算法则提升了多目标算法的效果，总体表现优于未改进的多目标算法和单目标算法。不同算法在进化过程中的准确度变化如图3所示。

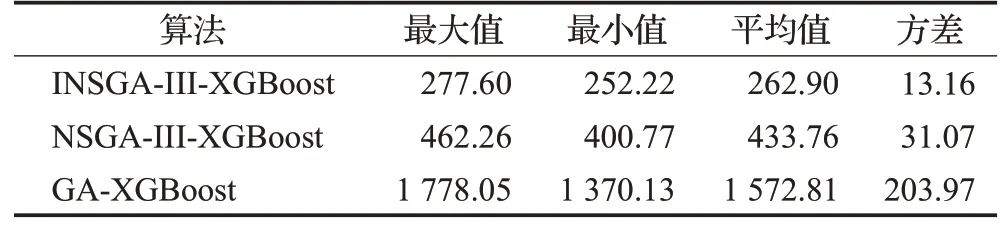
表3 运行时间对比Table 3 Comparison of processing time 单位：s

图3 进化过程准确度变化Fig.3 Change of accuracy in process of evolution

3.5.2 运行时间对比

表3展示了三种算法的运行时间对比。表中可以看出，本文提出的INSGA-III-XGBoost算法所需的运行时间最少，相比NSGA-III-XGBoost 算法平均运行时间缩短了39.4%，而相比于采用单目标优化的GA-XGBoost算法，平均时间缩短了83.28%。INSGA-III-XGBoost算法的运行时间方差最小，体现了INSGA-III-XGBoost算法在运行时间方面的稳定性。其运行时间较小的原因是，算法在选择了较少特征的同时选择了合适的提升树结构并动态调整了学习率，避免了大量不必要的计算开销，从而提高了运行效率。

3.5.3 综合比较

运行时间、选择的特征数、准确度是三个最重要的指标。表4 展示了三个数据集的不同评价指标的平均值。算法运行时间平均为4.38 min，选择特征数平均为20，平均准确度为88.74%。表中可以看出，本文提出的INSGA-III-XGBoost 算法综合运行时间最短，选择的特征数最少，且准确度最高，即性能表现最好。

表4 平均指标综合比较Table 4 Comprehensive comparison of average metrics

3.6 不同特征子集对比

以恒生数据集为例，对四种不同的特征数据集进行对比，四种数据集分别输入XGBoost 训练预测，结果如表5 所示。其中，历史特征数据集，仅包含原始的五个特征。其他特征数据集包含前人研究中常用的18个特征。所有特征数据集是本实验拓展特征阶段得到的81个特征，最优子集数据集为本文提出算法INSGA-IIIXGBoost选择出的最佳特征子集，相比于所有特征数据集，减少了70个特征。

表5 恒生数据集的特征子集对比Table 5 Comparison of feature subset in HangSeng dataset

INSGA-III-XGBoost 算法从80 个特征数据集中选择11个最佳特征子集，对这11个特征进行分析，这是神经网络的“黑盒”模型不具备的优势。图4 展示了该最佳特征子集中的特征，按照重要性得分降序。BOLLM即布林线的中线是所有特征中重要性得分最高的，这说明其对预测股票的走势作用最大。

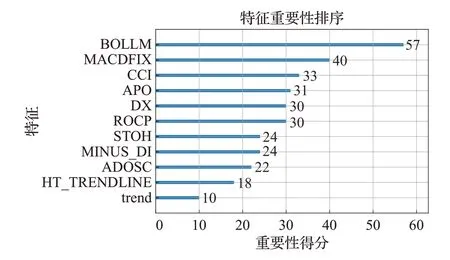
图4 最佳子集特征重要性得分Fig.4 Importance score of features of optimal subset

3.7 与基准模型对比

本文算法与经典的机器学习模型和不同层数的深度学习模型LSTM，和双向LSTM（bidirectional long short term memory，BiLSTM）比较。以恒生数据集为例，表6看出本文的算法具有最高的准确度、F1-score 和AUC。三种不同层数的LSTM迭代100次的实验结果如图5所示，LSTM 神经网络的训练准确度提高得很快，但是验证准确度先增后减，造成了过拟合的问题。

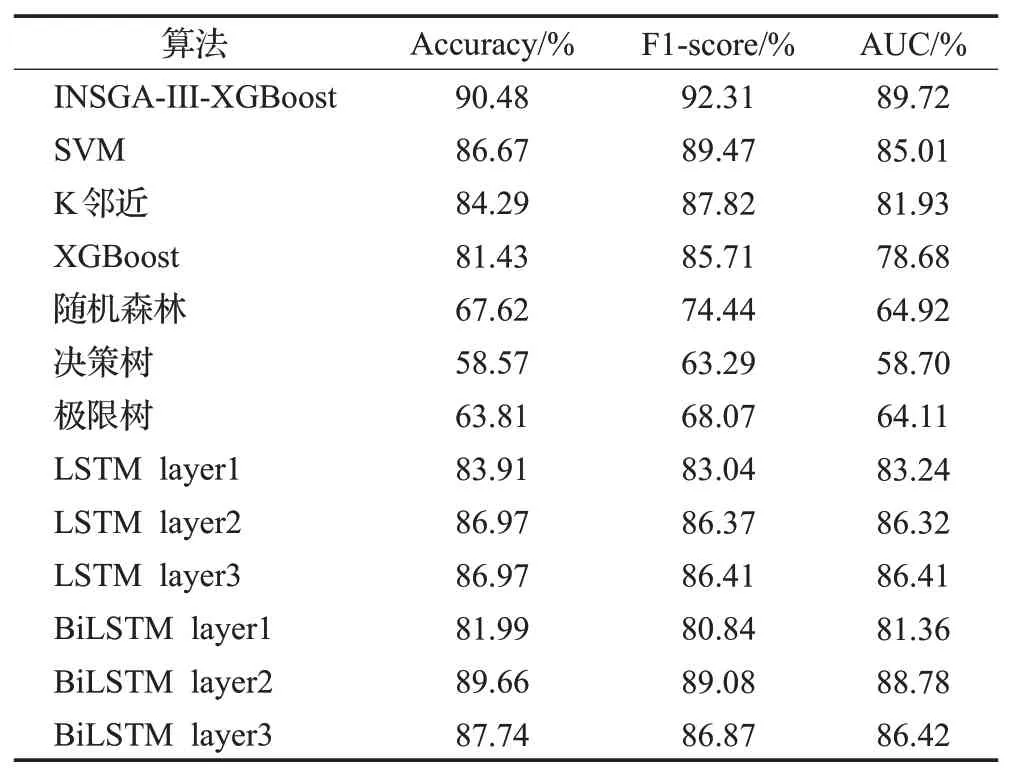
表6 基础模型对比Table 6 Compare with base model

图5 不同层数LSTM迭代过程准确度变化Fig.5 Change of accuracy in iterative process of LSTM with different layers

深度学习因为其强大的预测能力而应用于时间序列预测，但是模型的能力在很大程度上依赖于神经网络结构和超参数的调整。本文实验使用TPE 算法迭代优化LSTM神经网络结构200次。表7展示了INSGA-IIIXGBoost 算法和TPE-LSTM 算法的运行时间和准确度。表中可以看出，两者的准确度相差较小，但是本文提出的算法的运行时间仅为TPE-LSTM的0.99%。

表7 TPE-LSTM对比Table 7 Compare with TPE-LSTM

3.8 与基准研究对比

表8为本文与近几年来的基准研究对比，对比结果验证了本文提出模型的优越性。三大市场平均准确度比其他基准研究的准确度更高，从而验证了本文提出模型适应不同市场数据的能力。

表8 与基准研究对比Table 8 Compare with benchmark studies

3.9 其他多目标算法对比

将本文的提出的INSGA-III算法与其他多目标优化算法分别结合XGBoost比较性能，表9展示了恒生数据集实验结果。INSGA-III-XGBoost 算法的准确度最高，达到90.48%。图6为各多目标算法得到的帕累托前沿，纵轴为分类误差，即1-准确度。相比于其他多目标算法，INSGA-III优化效果最好，具有较小的解决方案大小和较低的分类错误率。

表9 多目标算法结合XGBoost对比Table 9 Compare with multi-objective algorithm combined with XGBoost

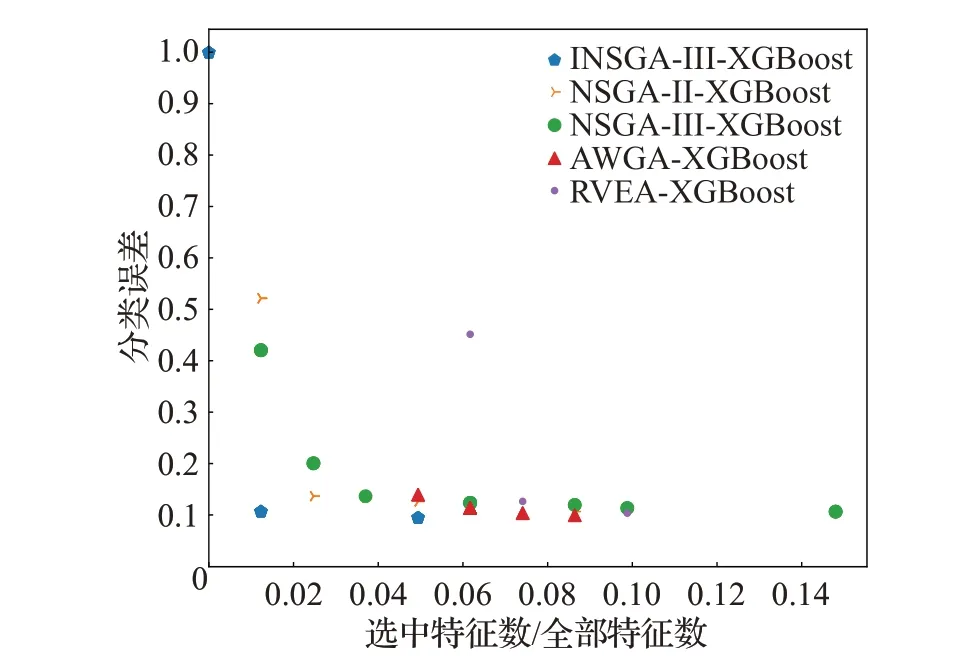
图6 多目标算法帕累托前沿Fig.6 Pareto front of multi-objective algorithm

4 结论

本文提出的INSGA-III-XGBoost 算法通过将两种过滤式特征选择集成的方法初始化种群，并将股票预测问题作为多目标问题，以最大化准确度和最小化解的解决方案大小作为优化方向，采用多染色体混合编码的方式同步优化了特征选择和XGBoost参数，对比其他基准研究具有最快的处理速度，解方案最小，预测准确度最高。在特征工程方面首先生成81 个特征，将原始历史数据5 个特征的预测准确度从77.62%提升到81.43%，而特征选择再选择其中11个特征作为最优子集预测准确度提升到90.48%，克服了“维度诅咒”的问题。在所有基础的机器学习模型和深度学习模型中本算法的预测性能最好。对比原始多目标算法和单目标算法运行时间分别缩短了39.4%和83.28%，运行效率高，适合短期交易系统的预测需求。对比默认参数的深度学习算法，预测性能平均高3%，而对比经过200代参数优化的TPE-LSTM虽然准确度只高1%，但是运行时间仅为它的0.99%，并且本文模型具有可解释性，实验结果给出了预测恒生指数走向的前11个关键特征及其重要性得分。