考虑冲突规避的自动化码头多AGV路径规划
张其娇,丁 一,秦 涛
1.上海海事大学物流科学与工程研究院,上海201306
2.上海海勃物流软件有限公司,上海200080
集装箱码头作为海陆物流的重要交通枢纽,在全球贸易中发挥着十分重要的作用。近年来,随着集装箱进出口吞吐量的增加、码头设备和技术不断革新升级,传统集装箱码头已向集装箱自动化码头发展。自动导引车(automated guided vehicle,AGV)作为水平运输设备,由于其自动化程度高、灵活性强、安全性好的特点,为自动化码头水平运输的重要设备之一。
AGV 主要运用在柔性制造系统和自动化码头中,一个良好的AGV调度和路径规划策略能提高系统整体的作业效率。对于AGV 路径规划问题,很多国内外学者投身于相关研究中,如冲突规避、最短路径以及协同作业等。孙毛毛等[1]和王晓军等[2]分别采用预先-实时规划和离线-在线两阶段方法对仓储系统中的AGV 实行路径搜索和冲突规避。与仓储中心不同,码头作业需要考虑到岸桥装卸作业环节和集装箱任务的时效性,且需要对突发事件进行灵活应变。Zhong等[3]、Murakami等[4]、杨雅洁等[5]针对自动化码头的AGV 路径规划使用混合整数线性规划建立数学模型,以实现AGV 的无冲突路径规划。然而在以上研究中,由于AGV 只能在固定时间段行驶在固定路段,因此对于多小车问题来说降低了路径利用率,从而影响作业效率。
在路径规划问题中,作为寻路的经典算法,A*算法是很多改进寻路算法的基础。张新艳等[6]、杨周等[7]、Jia等[8]提出了一种基于时间窗的改进A*算法以实现动态的AGV无碰撞路径规划。宋宇等[9]将A*算法与粒子群算法相结合,在缩短路径的同时降低了机器人的平均转折角度数。牟德君等[10]将A*算法中的距离代价函数改为时间代价,并引入转向和拥堵代价以减少AGV 转向次数,躲避拥堵路段。然而这些离线算法并不适用于实时性要求比较高的场合。从Korf[11]的开创性研究开始,实时启发式搜索已经被研究用于单智能体探路问题中[12-14]。在A*算法基础上,Sigurdson 等[15]在此基础上提出了一种用于多智能体寻路的实时启发式搜索算法,并与FAR[16]进行对比,表明该算法完成率更高且完成时间更短。Li等[17]首先使用多值决策图进行冲突分类,再使用两层搜索来为多智能体寻找满足无冲突约束的路径。Koenig 等[18]通过更新A*搜索之间的启发式算法来加速具有相同目标节点的重复A*搜索,结果表明自适应实时搜索A*以更小的代价跟踪轨迹,但其并未考虑到多智能体之间的相互影响。
由上可以看出,虽然目前已有众多学者在多AGV路径规划方面提出各种研究,但多数只考虑到静态环境下的无冲突路径,忽略了时间和空间特性,而现有针对动态环境提出的实时避碰方法忽略了多AGV之间存在的协作性,无法对突发事件进行灵活应变。且在以往研究中,对AGV 的集中式控制导致计算量巨大易造成控制中心崩溃,分布式控制由于AGV 之间通信困难而容易形成死锁。因此,本文结合两种控制方式的优点,针对环境多变的码头水平运输作业,采用混合式控制方式,如图1 所示。将AGV 在行驶过程中与其他AGV 可能产生的同向、相向或交叉冲突视为动态冲突,让每个AGV 单独运行加权实时A*算法规划路径,将实时搜索的路径信息上传给控制中心,由控制中心实现路径信息共享,根据共享信息各AGV 使用二叉树原理进行无冲突规划以实现动态冲突的规避。最后将该方法与普通A*算法进行比较,表明在同时满足路径长度较优的情况下,本文的方法在多AGV 作业的冲突规避和计算时间方面表现的效果更优。

图1 混合式控制方式Fig.1 Hybrid control mode
1 问题描述
采用传统的垂直码头布局,以进口箱作业为例,水平运输工具为AGV。AGV以恒定的运输速度经过水平运输区域,随后到达任务指定堆场。以某自动化集装箱码头为例,其平面布局如图2所示,左侧为岸桥作业区,右侧为堆场作业区,中间为AGV 水平运输作业区。其中,水平运输作业区中间部分为AGV缓冲区,阴影区域为空闲AGV 停车区,该阴影区域对于正在进行水平运输作业的AGV是不可通行的,将其视为AGV的静态障碍。由于运输任务的不同,AGV 从岸桥作业区到堆场作业区的运输路径也会不同,由此可能产生冲突。特别是在岸桥作业区,由于码头布局的特殊性,水平运输任务的起始点均在同一侧,当多个运输任务同时开始时,在该侧最容易产生冲突。本文的研究目标是在其水平运输路线中为多AGV 规划出一条无冲突、无拥堵且运输时间最短的行驶路径。

图2 自动化集装箱码头布局Fig.2 Layout of automated container terminal
在自动化码头作业环境中,每个AGV 需要从岸桥移动到任务指定的堆场以完成运输任务。假设AGV速度恒定且每个AGV每次只运输一个40英尺集装箱,对涉及到的相关参数变量及其意义说明如下:
(1)参数
n:地图中的节点;
n′:节点的后继节点;
c:节点之间的距离;
t:时间单位;
A:一组AGV集合;
d:AGV之间的直线距离。
(2)变量
ε:启发式的权重系数,ε≥1;
vision:AGV之间的安全距离;
lookahead:算法每次执行的搜索深度,大于等于1的整数。
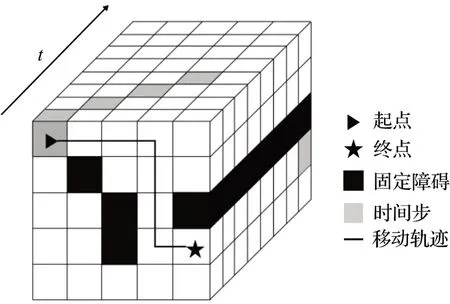
将AGV在运输路径中不可行驶的区域视为静态障碍,在运输节点碰到的其他AGV 视为动态障碍。一个AGV 每次仅完成一个任务,作业中途不可返回。当d (1) (2)两个AGV 将在同一时间步的直线距离小于安全距离。 不断重复上述搜索的过程直至ai到达目标节点搜索终止,从到之间形成一条路径P(n)即为所寻路径。 实时A*(RTA*)在移动前会执行一个固定的计算以确定合理的下一步移动,直到达到目标状态。令每次执行的搜索深度为lookahead,并让每个AGV运行一个单独的实时启发式搜索,将其他AGV视为障碍物,若即将产生冲突(d 虽然每个实时搜索算法总是朝着估算成本最小的节点移动,但随着算法运行,已遍历节点的估计距离变得比未遍历的节点高。为解决这个问题,在RTA*的基础上为启发式值h添加一个使得算法收敛速度最优的权重系数ε,从而减少算法在CPU 中的运算时间,加快算法搜索。在该算法中,g表示AGV 与岸桥作业点的实际距离,h采用的是码头实际中的距离计算公式:曼哈顿距离,表示AGV与堆场作业点的距离。如式(1)所示: 设h*(n)是ai从节点n到堆场作业点的实际距离,h(n)是其下界值,用hε(n)表示ai在节点n的ε下界值,则有:为保持估计距离的一致性执行式公式(3)、(4)操作: (1)评估函数 对于所有的相邻节点,计算评估函数如式(5)所示: (2)启发式规则 根据式(4)更新hε(n)。当同时存在多个最小fε(n′)值时,选择最小hε(n)的节点。另外,对于由任何移动指令生成的每个节点n和每个后继节点n′,从n到的估计距离不大于从n到n′的距离加上从n′到的距离。h(n)需满足以下条件: (3)行为选择 根据指令,ai移动到具有最小fε(n′)值的邻居节点n′处。如式(9)所示: 此时,从节点n到目标节点的路径P=(n0,n1,n2,…,即为所求路径。 多AGV并行能有效提高路径利用率并提高作业效率,但由于各AGV之间无法共享实时位置信息,导致行为缺乏协调性,同时进行运输作业时很容易发生冲突。为实现路径信息共享,引入第三维度:时间t,形成时空三维坐标(x,y,t),表示AGV在时间t时处于位置(x,y)[19],AGV 将时空位置信息上传给控制中心,由控制中心检索各AGV路径,实现各AGV的实时位置共享。 如图3所示,AGV在t=0 时从起点出发,在t=7 时到达终点。与传统算法只记录位置的空间二维坐标(x,y)相比,时空坐标精确记录下每个AGV 在某一时间点的位置,通过时间检索出同一时间步各AGV 的位置信息,从而方便检查有无冲突发生。 图3 时空图Fig.3Space-time map 为解决多AGV 之间的动态冲突并降低运行时间,对AGV 进行分组规避,使用二叉树原理对每个时间步中的节点进行分支,通过检索时空坐标实现路径信息共享,判断分支节点是否存在冲突,并对冲突节点的AGV重新规划路径。首先使用2.1 节中的WRTA*对每个AGV进行单独地路径搜索,再检查一对AGV的路径是否相互独立,若独立,则该组路径为合理路径;若在相同时间步长发生冲突,则对该组AGV 进行重新规划。由于WRTA*每次搜索的深度是固定的,且AGV在重新规划时有等待和绕行两种选择,从而避免了搜索过程中可能陷入无穷分支的死循环。图4 为进行动态冲突规避的单次实时路径搜索流程,循环执行该流程直至各AGV到达相应的目标节点。 图4 单次实时搜索流程Fig.4 Process of single real-time search 其中,动态冲突的判断如图5所示。在图5中,一对AGVa1、a2从各自的起点分别向目标点移动,且不可经过另一小车的目标点。首先执行路径搜索,分别得出其在特定的时间步长内可能的移动路径,之后共享路径,将这两条路径在相应的时间步长里合并成一组路径再进行冲突检测。 图5 二叉树冲突判断原理Fig.5 Principle of binary tree conflict judgment a1、a2分别在t=1、2、3时存在可能的冲突点,由图5(c)可知主要冲突点在t=3 时的节点(3,3)处。首先在t=0 时在起始节点对邻居节点的合法性进行判断,即a1和a2需要在节点(1,4)、(2,5)处舍弃共同的邻居节点(2,4);在t=1 时选择合法邻居节点进行路径搜索,同理,舍弃(2,3)与(3,4)节点;此时,a1和a2从在t=2 时有且仅有唯一的共同邻居节点(3,3),因此需要重新规划路径,这里只列举重新规划的两种解情况,如图6所示。 图6 重新规划的两种解Fig.6 Two solutions of replanning 在以上两个解中,a1路径均不变,Solution1为a2绕行的结果,Solution2 为a2在节点(2,5)处等待1 个时间步长。可以看出,此时a1与a2在各个时间步均不存在冲突,两个解均为合理路径。由于Solution1的总路径长度为13,Solution2的总路径长度为11,故选择当前阶段总路径最短的Solution2为优先解(若同时出现两个或两个以上相同长度的解,随机选择一个作为最优解)。之后将得出的解路径记作a12,与第三个小车a3共享路径信息,重复以上步骤进行冲突判断与规避。 为有效描述港口水平运输作业环境,参照某自动化码头AGV 局部水平运输作业环境,将其转换成大小为20×20 的栅格图,栅格中心点为坐标点,相邻节点距离为1。在该栅格图中,当AGV之间的距离至少为对角线长度时可以避免AGV的相向、同向和交叉冲突。因此,两种算法均使用安全距离参数进行搜索,以时空坐标(x,y,t) 记录路径表,在CPU 为Intel Corei5-1135G7 2.40 GHz、内存为16 GB 的Windows10 上使用Python3.7 版本进行算法运行。令表示一对AGVai和aj在时间步长为t时产生的动态冲突,记录两种算法的冲突数量、路径长度和运行时间,综合比较两者的运行效果。 任务安排如表1所示,AGV需要在相应的岸桥作业点经由行驶车道避开缓冲区到达指定的堆场作业点。已知生成4个任务请求,岸桥作业侧共有7条车道,堆场作业侧共有6条车道。 表1 AGV任务表Table 1 AGV task list 图7 AGV路网栅格图Fig.7 Grid map of AGV road network 在搜索到堆场作业区的目标节点前一直使用2.1节中ε=2、lookahead=4 的WRTA*进行实时路径搜索,即AGV 在岸桥作业区的起始节点移动前计算深度为4 的搜索,同时结合3.2 节中的动态冲突规避方法对搜索结果进行冲突检查和规避,得到长度为4 的无冲突路径,并向其方向移动,然后再次执行同样的搜索,直到抵达目标节点。记录各AGV无冲突路径如表2和图8(c)所示。 表2 实时搜索路径表Table 2 Path table of real-time research 图8 实时搜索路径图Fig.8 Path map of real-time research 由表2 可知,a2共执行8 次搜索、a1和a3均执行9次搜索、a4共执行10次搜索后到达目标节点。其中,在执行第一次和第二次搜索时会有冲突产生,每执行一次搜索后进行动态冲突规避,重新规划路径,其余搜索均为无冲突。 截取冲突路段进行分析,如图8(a)所示,a2和a3执行第一次搜索在t=1 时会产生冲突。此时a2在节点(1,11),a3在节点(1,12)处,两车距离,故需要进行冲突规避。规避后a3保持路径不变,a2绕行,重新规划后的实际移动路径如图8(b)所示,当t=1 时a2在节点(2,10)、a3在节点(1,12)处,再进行第二次搜索。如图8(b)所示,a1和a3在执行第二次搜索时在t=5 处会产生冲突,此时a1在节点(2,8)、a3在节点(2,9)处,规避后a3保持路径不变,a1绕行,此时a1在节点(3,7)、a3在节点(2,9)处。全部搜索完成后得到实际无冲突路径如图8(c)所示。 标识各AGV 路径中出现的共同节点,如图8(c)所示,根据表2 验证路径的合理性,如标注①处a1与a3分别在t=3 和t=8 经过节点(2,6)。标注②处a1与a3分别在t=4 和t=7 经过节点(2,7)。 同理,各AGV均在不同时间步经过③~⑧处节点。由上分析可知,各AGV在不同时间步经过共同节点,连续两个时间步长内各AGV之间的距离均满足d≥vision的无冲突要求,各AGV之间不存在冲突,该路径合理。 在执行普通A*进行搜索时得到各AGV路径如图9所示。对其冲突区进行分析,AGV 之间共产生9 个冲突:a1与a3在t=5 和t=6 时产生冲突在t=1、t=2、t=3 时产生冲突和;a1与a4在t=7 和t=8 时产生冲突和;a2与a4在t=4和t=5 时产生冲突 图9 普通A*搜索路径图Fig.9 Path map of ordinary A* search 同理,对其使用3.2 节中冲突规避的方法进行多AGV并行运算,得出各AGV的无冲突路径如表3和图10所示,各AGV在不同时间步经过共同节点①~④。 表3 普通搜索的无冲突路径表Table 3Conflict free path table of ordinary research 图10 普通搜索的无冲突路径图Fig.10 Conflict free path map of ordinary search 对3.2 和3.3 节的结果进行分析如表4 所示。在算法消耗时间方面:使用实时搜索计算时间共消耗了7.061 6 s,使用普通搜索的计算时间共消耗了7.937 2 s;在冲突数量方面:在未进行动态冲突规避时,WRTA*共产生2 次冲突,普通A*共产生9 次冲突;在路径长度方面:两种方法得出的4 条路径总长度均为110。为进一步验证算法有效性,设置不同AGV 规模下的路径规划算例,得到的结果如表5所示。 表4 结果分析Table 4 Result analysis 表5 不同AGV规模下的结果分析Table 5 Analysis of results under different AGV scales 由以上结果可知,冲突数量和计算时间会随着AGV数量的增加而增加,WRTA*在计算时间和产生的冲突数量方面优于普通A*。另外,可以看出无论使用WRTA*还是普通A*,结合使用2.2节中的动态避障方法最终都能得到无冲突路径。 码头作业是一个实时作业环境,与普通A*搜索相比,WRTA*算法由于每次执行固定深度的搜索,在作业中途遇到如环境变化、设备故障、目标节点改变等需要终止算法的突发情况时其损失代价较小。而普通A*由于在执行路径的第一步之前就计算好整个解路径,一旦碰到突发情况整个搜索将前功尽弃。特别是在地图较大的情况下,由于一次计算全局解,普通搜索储存的路径表更长,易造成存储负担,降低计算速度。因此,在码头作业环境中,本文提出的实时搜索方法由于每次执行固定深度搜索,且在搜索过程中伴随冲突规避,故在多AGV作业的动态冲突规避和计算时间方面表现的效果更优。 针对多AGV 路径规划问题,考虑到码头作业的实时环境和多AGV 之间的行为影响和协作性,本文在混合控制模式下使用WRTA*搜索算法寻找路径,采用时空三维坐标以实现实时路径信息共享,同时结合二叉树原理进行冲突判断和规避,有效避免了多AGV 作业产生的冲突问题,最后通过算例与普通A*算法相比较。结果表明,WRTA*算法的消耗时间较小,且由于每个AGV单独使用加权实时A*交错规划路径,产生的冲突数量远少于普通A*算法,验证了实时搜索方法的有效性。 本文是在AGV调度以及任务分配顺序已知的前提下进行的路径规划,在日后研究中可以结合任务调度在避障过程中引入任务优先级规则或其他优先级规则进行系统性优化。2 多AGV路径的冲突规避
2.1 加权实时A*算法(WRTA*)
2.2 动态冲突规避



3 算例分析
3.1 算例描述


3.2 实时搜索
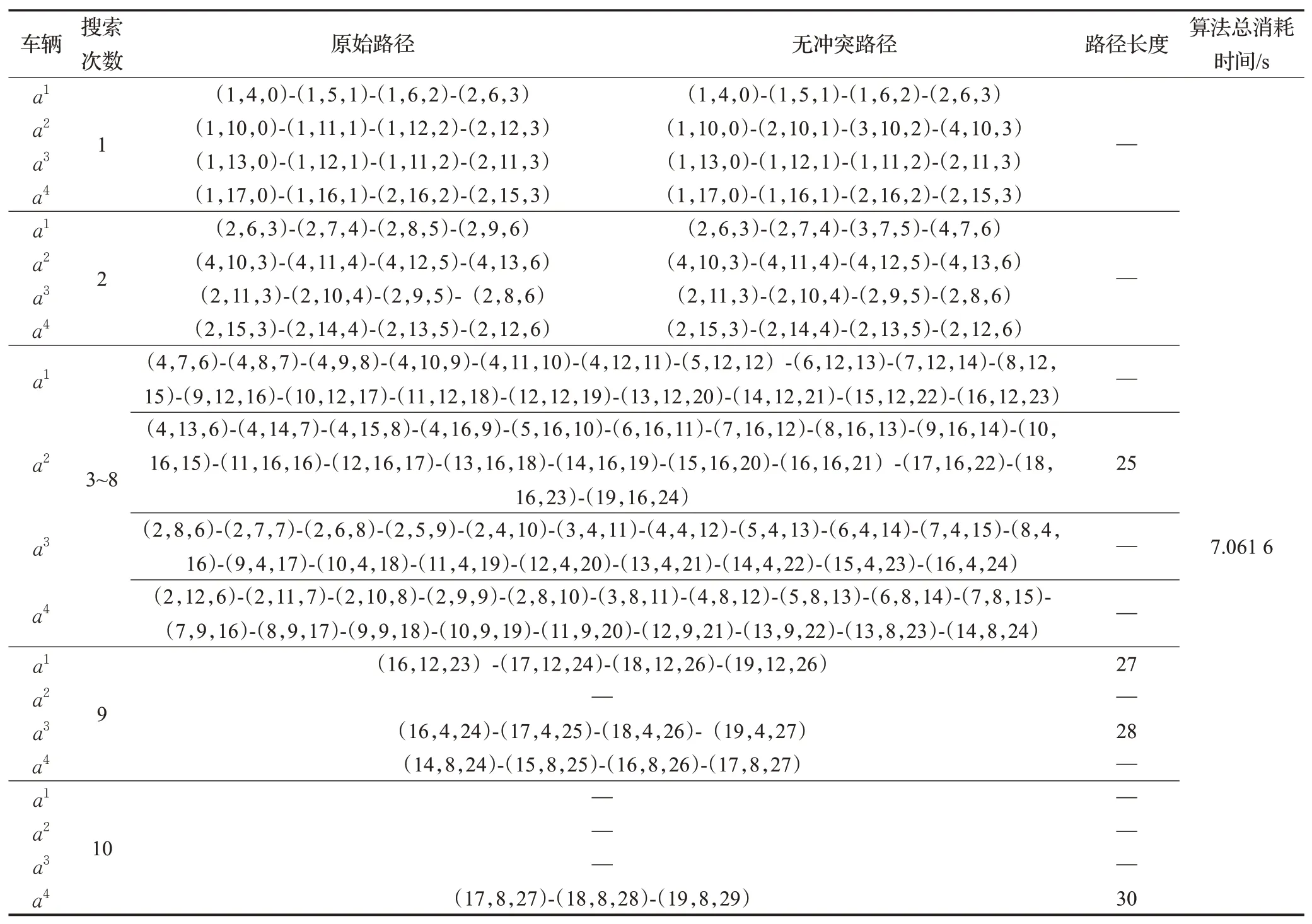

3.3 普通搜索


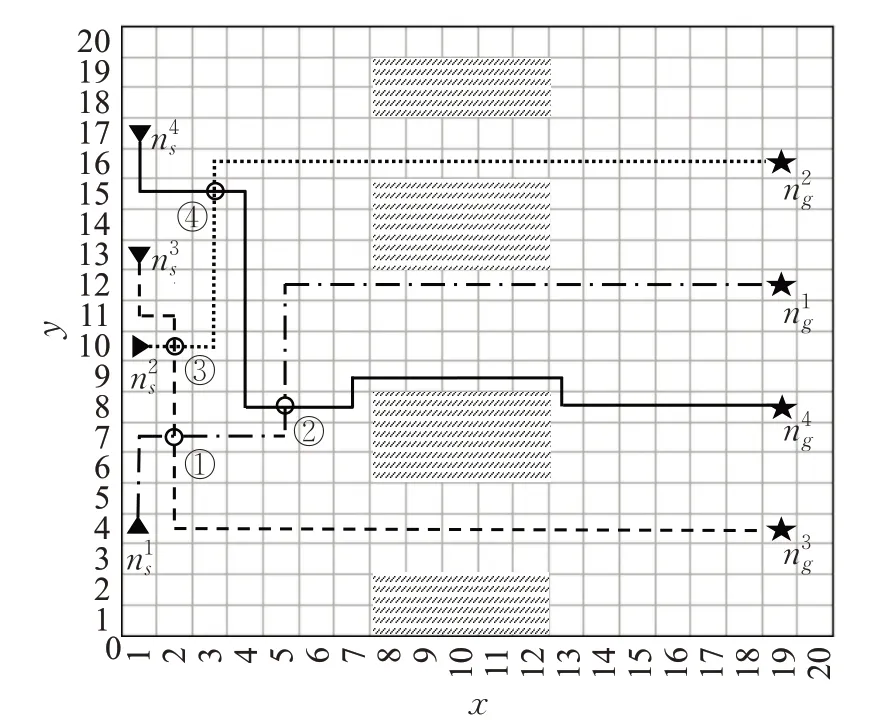
3.4 结果分析


4 结论

