空间感：在多元活动中自然生长——以小学中段“计量单位”教学为例

●李庆英

《义务教育数学课程标准(2022 年版)》指出，量感主要是对事物的可测量属性及大小关系的直观感知，对度量意义的理解及真实情境下的测量估计等[1]。空间计量单位是一个连续性的知识，蕴含有知识、方法、思想的同构。

空间计量单位的教学离不开直观教学。新课标指出：直观，通常没有经过严格的逻辑推理，却往往能把握对象的全貌和本质。

一、借助图形表征计量单位，助推量感生成

计量单位教学分布于小学各个阶段，从一维空间观念到二维空间观念再到三维空间观念，每个阶段呈螺旋上升趋势，图形的认识、图形的运动及图形与位置教学，知识脉络与根源相当清晰[2]。前后知识点之间的联系也有共同点的支撑和过渡。因此，在通观教材后，点线面的结构将会在学生大脑中形成模型，进而建构从线到面，由面至体的探索过程。

（一）情境教学，借图表征

小学是具体形象思维逐渐过渡到抽象逻辑思维的阶段，数学中的直观是借助经验、观察、测试或类比联想产生的对事物关系直接的感知与认识。在实际教学中，动手操作也就是提供学生直观想象的基础，实践中有认知，认知中有感悟，感悟中有联系。

在三年级上册分米、毫米、米的复习课中，为学生设计上台表演的情境，让学生分别扮演“毫米”“厘米”“分米”“米”，复习知识的同时，贯通知识的前后联系。

生1：大家好，我是“毫米弟弟”，在生活中，一些非常小和薄的物体长度都由我来做测量单位，比如1 分硬币、1 元硬币、1 张公交卡的厚度等，直尺上的1 小格就是我。

师：请在纸上画出“毫米弟弟”的长度。

生2：嗨，“毫米弟弟”你好，我是你的“厘米小哥”，在生活中，我一般测量比较小的物体长度，如指甲盖的宽度、开关的宽度或厚度……直尺上10 个你就组成了1 个我。

师：请在“毫米弟弟”身体上画出“厘米小哥”，想一想会有几个这样的“毫米小弟”呢。

生3：“厘米小哥”你好，我是你的“分米哥哥”，10 个你就组成了1 个我，大家很容易误会我的长度，所以，找找你们身体上的我，比如1 拃长，课桌椅的高度……都可以用到我，我在生活中也是无处不在的。

师：请在“厘米小弟”身上用另一种颜色画出“分米哥哥”，看看可以画几个。

在学生喜闻乐见的故事串联中，厘清关系，不知不觉中，知识已变成故事的主线，让原本生硬抽象的知识变得生动有趣，进而对长度单位的表象、每个长度单位的长短有了初步的感知。

（二）图形对比，厘清思路

在认识面积一课中，从一些物体的表面或平面图形入手，比较它们的大小引出面积的概念；再从数格子比较法中引出面积单位。首先在理清面积与相关知识（周长与长度单位）的关系后，通过动手操作、摆方格及画图来突破重难点。

师：老师拿出了一个盒子，这是个物体，我正在摸这个物体的什么呢？

生：外表、外面、表面……

师：摸一摸数学书的表面和练习本的表面，比一比谁大谁小，你是怎么比的？

生1：将数学书和练习本重合起来就知道了。

……

通过画图、比较和推理等活动培养学生的直观想象，不但顺应了学生天性，还使教学过程动静相宜、张弛有度，无痕地渗透数学思想，让学生插上了想象的翅膀，在轻松的学习氛围中积极思考，深入挖掘，探索创新。在此过程中，教师精心设计问题和活动，耐心等待，为学生提供充足的时间，教学中要善于捕捉课堂中的亮点和生成点。

（三）头脑成像，丰富感知

著名特级教师曹培英教授指出，各种领域各有侧重的研究思路，怎样基于儿童成熟、适时教学干预发展空间观念，是计量教学内容中非常关键的思考点和落脚点。

从二维空间观念到三维空间观念，借助直观模型，让关系更明确。

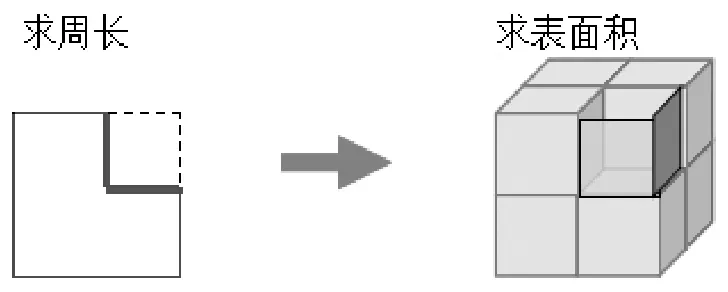
图2

图3

直观想象的载体就是图形，数与形的结合成为关键。史宁中教授说：“数学知识的形成依赖于直观，数学知识的确定依赖于推理。”教师需要抓住有代表性的数学教学内容，创设适合学生生活经验的情境，巧设疑问，不断引导学生观察、尝试、再体验、再发现，让学生在丰富的数学活动经历中积累直观想象的经验，进而培养直观想象的能力，丰富“量感”。

二、借助操作领悟计量单位，奠定量感基础

新课标明确要求计量单位应该在现实的情境、具体的生活中去认识和教学。学生只有通过有趣的操作活动才能对一些抽象的“量”获得感受。

（一）“打点立柱”，意在联系

在教学过程中，几何直观的呈现虽不多，但也能见其影，知识之间的内在联系也有所体现。如在教学分米的认识时，遵循教材的逻辑关系，尝试让学生在丰富的操作体验中形成认知经验，将知识融会贯通，有意识地搭建起知识间的沟通桥梁[3]。

量一量：正确量出纸条（课前自行准备的10 厘米长的硬纸条）的长度，巩固计量物体的基本方法，明白“10 厘米就是1 分米”。（实物）

比一比：将纸条放在拇指和食指之间，感受1 分米大约是1 拃长，建立表象，制作身体上的尺子。课堂小结时还可以延伸拓展，让孩子们感受一下一庹的长度大约有几个一拃。（感知）

想一想：抽离纸条，定格1 拃长，体会1 拃长约是1 分米，再观察同桌比画的1 拃长，并进行比较。用身体上的这把“尺子”量一量课桌的长大约是几分米。通过体验活动丰富认知，积累经验。

验一验：再用手空比画1 分米，放到直尺上验证，再次体验。

摆一摆：用1 厘米长的纸条在1 分米的纸条上摆一摆，猜想需要多少个1 厘米，或是先想能摆多少次。

悟一悟：厘米与分米之间“你中有我”的关系，10个1 厘米是1 分米，1 个1，2 个1，3 个1……在操作和语言表达中，发展空间想象能力和数学表达能力，从而感悟到进率是“10”的意义，体现知识间的关联。

通过发现—操作—理解—经验—内化的过程，引导学生交流、评价、体验，从而发现这几个长度单位间的联系，对这几个计量单位的含义也有了初步的感知[4]。

（二）“连柱成梁”，重在推理

从实物中抽象，再将抽象用具象的方式直观呈现，让思维外显，种下“意识的种子”。

通过操作领悟关系：“拇指连”（1 个拇指的指甲盖约1 厘米，10 个指甲盖拼起来就是1 分米）。

借助实物呈现关系：摆小棒（假设1 根小棒是1厘米，10 根这样的小棒就是1 分米）。

小棒有多长，不是本质，在于10 根小棒组成1分米。

结合图示析出关系：学生画图（直条图、数线、1条被平均分成10 份的线段图，1 条1 厘米、下面1条10 厘米）。

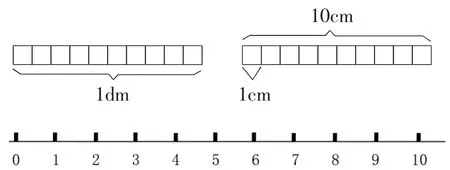
图4

大胆创新，融会贯通：计数器（个位设定为厘米，十位设定为分米，“满十进1”，10 个1 厘米就是1 分米）。

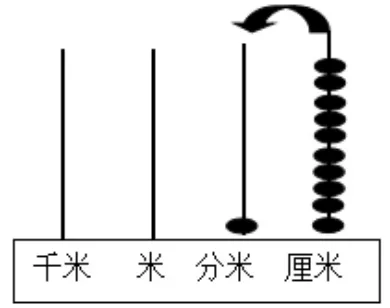
图5

联系生活，形成经验，在各种尝试中延续，闭眼想象：如果将1 分米延长，2 个1 分米就是20 厘米，3 个1 分米就是30 厘米……用类似的思考过程研究分米和米的关系，发展学生的空间想象力。依次联系1 毫米、1 厘米、1 分米及1 米的关系。

（三）“连梁成网”，旨在建模

“几何直观就是画图（看图）想事。”——认识面积的过程中，大量的操作和体验建立在“量感”之上。

在认识“面积”的教学中，借助长度单位的学习经验，让学生通过探索长度单位与面积单位之间的联系和区别，产生统一面积单位的需求，体会平面图形和物体的面有大有小，认识面积单位。从“线”发展到了“面”，这是空间观念的一次飞跃。在面积单位的换算中，根据学生易于接受直观性强的事物的特点，有意识地为学生提供了以下材料：方格纸、透明方格、直尺、学生自制1 平方厘米的小正方形，让学生动手操作，探究1 平方分米与1 平方厘米的关系。

摆一摆：密铺、一排10 个，共10 排。

画一画：用直尺画出小方格，感受面积的意义。

学生在充分的动手操作中体验、感悟，使面积单位表象更清晰、更具体，“量感”也就建立起来了。

想一想：1 分米等于10 厘米，边长为10 厘米的正方形面积为10×10=100 平方厘米。将形状“印”在脑中，理清关系。

在活动的基础上，通过计算、推理，同样也能得到1 平方分米=100 平方厘米的结论，头脑里的知识脉络在理性思考和直观操作的基础上搭建起来，为后续学习平方千米提供想象依据和操作经验，促进了学生的直观呈现[5]。

三、借助实践建模计量单位，促进量感提升

学生量感建立的基础是各种实践活动，充分感知计量单位，形成计量单位的表象，从而以计量单位作为参照，逐步发展量感。教师在教学中可以将量感的培养蕴含在各类实践活动和实际运用中，体验有层次的“量”。

(一）通过实物感知，内化量感

培养估测意识、提高估测能力是新课标的一项重要内容，也是培养学生“量感”的重要途径。测量的目的是通过使用测量工具，得到精确的测量数据；而量感主要表现为在不借助工具的前提下对数量有比较准确的感知。

在学习四年级上册“公顷”和“平方千米”这两个比较大的面积单位时，教师设计了课外实践活动，把学生带到学校操场上，先帮学生估一下跨一步的长度，再让学生沿着操场边沿跨步走大概100 米的距离（大约200 步），再沿着另一个方向走两百步，让学生算一算边长大约是多少米、面积大约是多少平方米，从而体验边长为100 米的正方形面积是10000平方米，也就是一公顷，100 个这么大的操场就是1平方千米。再让学生估一下自己的学校占地面积大约是多少公顷。经常这样练习，学生的估算能力和测量能力都能得到提高，对计量单位的把握也就更加精准，量感也就能得到进一步的发展。

（二）通过估测活动，丰富量感

重量单位“克、千克、吨”对于三四年级的孩子来说是无法真正体会的。因此教师在教学“克与千克”时可以借助生活中的一些实物让学生亲身感受一下，帮助学生建立单位表象。比如一个回形针、一粒花生米、一枚两分的硬币、一张A4 纸、一个乒乓球等大约是一克，两瓶500ml 的矿泉水、15 个鸡蛋、三袋牛奶（每袋330 克）大约是一千克。教师课前让学生准备好这些实物，教学时让学生掂一掂，体验一克和一千克究竟有多重，再通过实物判断哪些物体比一千克或者一克轻，哪些物体大约是一千克或者一克……

通过这样的丰富多彩的实践活动，学生借助生活中熟悉的实物来建立单位表象，对“克和千克”这样的重量单位的概念逐步清晰，对量的感受也由直观表象走向抽象推理，加深了学生对单位本质的理解，丰富了学生的量感体验，从而促进了“量感”的提升[6]。

（三）通过实践应用，深化量感

学习是为了应用，而知识只有在应用中才能被学生真正理解和掌握，也只有在实践中才能进一步深化认知，体现知识的价值。

基础练习：

1 平方千米＝（）公顷＝（）平方米

一个足球场约7000（）

学校占地面积约4（）

填好后引导学生说说自己的想法。

深化练习（举生活中的实例）：

比1 公顷小的面积有_______________________

比1 公顷大的面积有_______________________

拓展练习：

1000000（）-100（）＝0（）

实践应用的三个练习层层递进。第一个基础练习是对公顷和平方千米的整理和巩固，发展学生对量的实际意义的认识，强化学生的认知；深化练习让学生运用所学的公顷和平方千米的知识举生活中的实例，培养学生的估测能力，修正面积单位的表象，提高量化的估测能力和表达能力；拓展练习让学生用学过的面积单位进行选择，深化面积单位的量感，为后续学习小数和分数化单位做铺垫[7]。

总之，小学生“量感”的培养是一个循序渐进的过程，而培养学生的量感是通过计量单位的教学来实现的，因此教师要优化计量单位教学的策略，让量感培养潜移默化地渗透到常态教学之中，让学生在多元化的数学活动中积累“量感”经验，发展量感[8]。