曲面磨削表面微观形貌建模方法研究

胡 宁 陈海锋

（湖南科技大学智能制造研究院难加工材料高效精密加工湖南省重点实验室，湘潭 411201）

文 摘 针对现有磨削表面微观形貌建模方法仅对某一类特定零件有效，提出了一种适用于空间曲面零件加工的磨削形貌建模方法。基于曲面磨削加工原理，建立砂轮坐标系与曲面零件坐标系之间的齐次变换矩阵，获得磨粒的三维运动轨迹方程。通过提出曲面区域逼近求解算法，建立曲面磨削表面微观形貌预测模型。并以展成法磨削齿轮和磨削轴承内套为例，得到两类实验与仿真结果之间的误差最大为11.338%和18.91%，验证了本文提出的预测模型的有效性与科学性。

0 引言

磨削作为一种去除材料的机械加工方法，广泛应用于发动机叶片、齿轮等复杂曲面零件的精加工工艺中。表面微观形貌作为反映磨削加工质量的重要指标之一［1］，在工程中得到越来越多的重视，为了对磨削后的工件表面微观形貌进行预测，国内外学者在其建模方法方面做了大量的研究。现有的建模方法可分为经验建模方法和理论建模方法［2-3］。其中经验建模方法是对大量的实验数据通过计算机进行总结拟合出表面粗糙度与加工工艺参数之间的预测模型。高钦［4］利用回归分析方法对磨削后的面齿轮表面粗糙度进行预测，并且验证了所建面齿轮表面形貌回归预测模型的准确性。田凤杰等［5］根据砂带磨削叶片后所得的实验数据建立了评价指标拟合回归数学模型，并且该模型可反映加工参数与叶片表面磨削后粗糙度的关系。与经验建模方法相比，理论建模方法是通过对砂轮上磨粒的运动轨迹映射至工件表面的过程进行数学描述，以获得表面微观形貌的预测模型［6］。ZHOU等［7-8］利用树脂黏合剂将蜗杆砂轮上的磨粒进行复刻得到砂轮形貌，并根据该砂轮形貌结合蜗杆砂轮与齿轮齿面之间的运动关系，建立了齿面微观形貌的预测模型。CHEN等［9-10］通过计算单颗磨粒的切削轨迹，及相邻磨粒轨迹的交点，根据布尔运算，获得齿廓的仿真形貌。梁志强等［11］通过研究砂轮形貌的仿真以及螺旋伞齿轮磨削磨粒的运动轨迹，结合干涉轨迹在面坐标系上遗留的坐标值进行伞齿轮理论微观形貌的建模。陈杉杉［12］提出一种考虑曲面曲率影响下的磨削加工表面形貌理论模型，该模型是将相邻两砂轮磨粒磨削过程中的残余空隙部分进行区域面积和残余高度值的计算，最终得到曲面形貌建模的一种方法。段练［13］根据磨粒接触半径和磨削曲面的等参数线之间的弧长得出可计算出磨粒切削加工曲面工件截面所遗留高度的理论公式，并以此建立叶片磨削后的仿真形貌。

综上所述，现有的曲面磨削表面微观形貌预测方法大多针对某一特定曲面零件，对其他类型的曲面零件适用性较差。因此，根据砂轮上的磨粒在空间曲面的磨削包络轨迹来建立具有通用性和普适性的预测模型。本文主要研究复杂曲面零件表面微观形貌与磨削工艺参数之间的关联规律，在科研生产中具有重要的工程价值和理论意义。

1 砂轮表面形貌建模

由于砂轮表面是由大量形状复杂且随机分布的磨粒组成。因此，将磨粒形状假设为不规则多面体，多面体由球体随机切割而成。

根据文献［14］，磨粒最大直径dgmax、磨粒平均直径dgave可表示为：

式中，M为砂轮磨粒的粒径号。

假设磨粒切削刃高度服从高斯正态分布(μ，σ2)，切削刃的露出高度h可由分布函数表示如下：

式中，A1为定量参数，文中该参数的值为1。

砂轮表面相邻磨粒的平均间距可表示为［15］：

式中，S为砂轮组织号。

为了保证两两磨粒之间不发生干涉现象，需要设定将两两磨粒间距大于其半径之和，因此对于空间中任意两颗磨粒Gi，j，k和Gl，m，n应满足下列公式要求：

式中，dgi，j，k和dgl，m，n分别表示磨粒Gi，j，k和Gl，m，n的直径。如不满足上述条件，需将Gl，m，n重新赋值并计算，最终可得到砂轮磨粒随机分布下的情况如图1所示。

图1 砂轮磨粒形貌图Fig.1 The morphology of grinding wheel

2 曲面磨削微观形貌建模方法

2.1 任意曲面磨削加工的坐标变换矩阵

空间曲面零件磨削过程如图2所示，曲面工件绕x轴转动，同时沿x正方向做进给运动，与此同时，砂轮随着变化的曲面改变主轴z方位并对曲面进行切削运动。其中O1-x1y1z1为曲面工件中心坐标系，Of-xfyfzf为曲面工件进给坐标系，O2-x2y2z2为砂轮磨削起始坐标系，为砂轮磨削结束坐标系，Os-xsyszs为砂轮与曲面的接触坐标系。

为了得到砂轮表面上的磨粒与工件接触时的变换矩阵，首先根据图2 中所示位置关系，O1-x1y1z1通过绕x轴旋转φ角度，沿x方向上移动距离s到达Of-xfyfzf，该s表示工件进给距离，上述变换过程的齐次坐标矩阵［16-17］可表示为：

s可表示为：

式中，vs为曲面工件的进给速度。另外该矩阵中φ表示曲率转角，可将其视为曲面轮廓线上每段微分区域对应角度的总和，但在特定条件下又可认为φ=ωt，此处的ω为工件转速。

根据图2 中所示位置关系，Of-xfyfzf通过z方向上移动距离ρ，y反方向上移动距离p到达O2-x2y2z2，对应的变换矩阵为：

该矩阵（7）中的ρ可表示工件曲率转动半径，p可由下式进行表达：

根据图2 中所示关系，假设O2-x2y2z2与的坐标中心处在同水平面上，仅砂轮主轴z的朝向发生改变，得到O2-x2y2z2将xOy平面和xOz平面旋转角度φ和λ变换到达。因此，可得到对应矩阵（9）：

当两坐标系存在相对位置偏差，在矩阵（9）的基础上，O2-x2y2z2沿z方向移动距离h，y方向上移动距离a，x方向上移动距离b到达，对应矩阵为（10）：

该矩阵（11）中θ为砂轮旋转角度，可由下式进行表示：

式中，ns为砂轮主轴转速。

假设磨粒G 位于砂轮上，根据任意曲面的磨削加工原理，将砂轮上的磨粒G 映射到曲面工件中心坐标系上的变换矩阵可表示为：

该公式即可模拟单颗不规则磨粒包络三维轨迹。

2.2 单颗磨粒的三维轨迹建模

以单颗磨粒为研究对象，截取磨粒在yOz平面上的轮廓如图3 所示。图3 中各点为不规则磨粒仿真截面上的顶点，选取截面中最外侧顶点，将其视为该磨粒的最大截面，其中BAC段为砂轮不规则多面体磨粒的切削工作部分［18］。单颗不规则多面体磨粒在赋值过程中，BAC三点均可由yOz坐标系进行表示，因此通过图3展示的部分，可得出角ξ为：

图3 不规则多面体磨粒截面示意图Fig.3 The cross section of irregular abrasive particles

设阴影部分为磨粒的切削区域，根据几何关系得到区域内磨粒与工件之间切削接触轨迹的坐标方程组：

式中，Gx，y，z为该磨粒的坐标值，dg为不规则多面体磨粒的外接球直径，β为切削区域的最大阈值角度。

在实际磨削对刀时，是以砂轮是否产生切削火花为基准再以预定的切削深度进给［2］，因此实际切削深度可表示为：

式中，dgmax为不规则多面体磨粒的外接球最大直径，ap为理论切削深度。为将切削深度考虑到单颗磨粒截面坐标方程组中，根据图3 中的位置关系，将坐标系中心定义在磨粒中心以上距离处，该距离数值为实际切削深度高度值ae。因此将式（16）与式（15）联立可得：

利用齐次坐标矩阵表达出单颗磨粒G 的工作截面状态，得到矩阵（18）。

将式（18）代入公式（13），可得到关于磨粒G 在曲面运动的三维轨迹方程组。对于任意空间曲面的磨削，只需根据磨削加工过程中，砂轮与工件坐标系的相对位置关系，对转换矩阵进行修改即可得到适用于该磨削方式下的三维轨迹方程组。

2.3 曲面磨削表面微观形貌建模方法

为了建立曲面磨削微观形貌，提出一种曲面区域逼近求解算法，其中算法的实现如图4所示：（1）首先根据图2 所示的曲面磨削齐次坐标变换矩阵得出单颗磨粒的三维切削轨迹方程，将已知参数代入方程中得到每颗磨粒切削轨迹对应在曲面上的映射值；（2）根据曲面磨削的实际情况，将曲面工件的运动转角进行等分，并生成求解区域，又由于在进行角度划分过程中会可能出现相邻两区域中心点之间的距离不一，为保证精度，需设置一个最大精度；（3）考虑到砂轮上磨粒众多且分布不均，将每颗磨粒的轨迹映射到曲面上的指定区域中，会导致计算量巨大，因此选取每个区域坐标点(gx，gy)为中心点，设置一个搜索范围，仅将搜索范围内的磨粒映射值进行保存；（4）计算每个划分区域中心点对应的曲率角度，将该角度纳入匹配磨粒映射值在区域内法线方向上的遗留高度值的考量中；（5）按上述方法，依次计算所有区域匹配下的磨粒切削工件表面的残余高度值，然后选取这些高度值中最小的值作为该区域的高度值；（6）然后将这些最小值连接形成曲面工件的最终磨削形貌。综上所述可得关于曲面磨削形貌的仿真算法流程见图5。

图4 曲面磨削表面微观形貌实现示意图Fig.4 Realization diagram of curved surface grinding profile

3 曲面磨削微观形貌建模方法应用与试验验证

3.1 曲面磨削微观形貌建模方法应用实例一

以齿轮展成法磨削为例，其磨削的工作原理如图6所示［19-20］，齿轮以x轴为旋转中心，逆时针与砂轮工作面做啮合运动，其中图6中虚线部分为蜗杆砂轮的齿形截面，砂轮工作面始终与齿面相切，又由于齿轮的端面齿廓为渐开线状，将渐开线基圆进行等角度微分，得到砂轮沿渐开线磨削的转角φi。根据上文提出的曲面磨削微观形貌的仿真方法，可知齿轮中心坐标系O1-x1y1z1通过齿轮的转角和x方向上的进给到达齿轮进给坐标系Of-xfyfzf，并计算渐开线方程为：

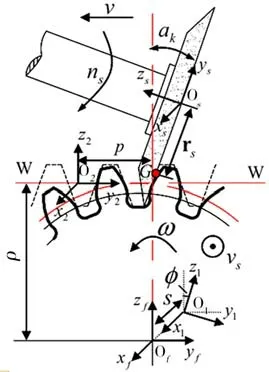
图6 齿轮展成法磨削坐标系变换示意图［10］Fig.6 Gear generation method grinding coordinate system transformation ［10］

式中，ρ为基圆半径。因为在磨削过程中，O2-x2y2z2和之间无位置偏移和角度的旋转，因此M22′为齐次单位矩阵，而M1f、Mf2和M2′f均为前文提到的矩阵。结合图6 齿轮展成法磨削运动关系原理以及相关参数代入式（21）可得关于砂轮不规则单颗磨粒相对于齿轮齿面磨削的三维轨迹方程组：

以三维轨迹方程组（20）计算后的z值为依据，通过本文提出的曲面区域逼近求解算法，可将齿轮展成法磨削形貌表达出来。

为了验证本文所建立的曲面微观形貌预测模型的有效性，采用蝶形砂轮对渗碳淬火硬化处理后的20CrMnTi 齿轮进行磨削实验，齿轮毛坯件和砂轮的参数如表1 中所示。实验结束后，用白光干涉仪（Wyko NT9100）测量实验齿轮进行表面微观形貌以及粗糙度。

表1 齿轮展成法磨削实验参数表Tab.1 The parameter table of gear grinding experiment

采用与实验相同的工艺参数进行仿真，得到仿真形貌如图7所示，所建齿轮渐开线齿廓形貌图与文献［10］中的仿真形貌基本一致。不同砂轮转速及不同进给速度下表面粗糙度的实验与仿真结果对比如图8、图9所示，随着砂轮转速的提升，砂轮在齿面磨削的次数增多，在多磨粒作用下，工件表面残余高度趋于稳定，使得表面加工质量上升；同理随着齿轮进给速度的不断增加，单位时间内切削磨粒数目减小，使得切削效果降低，从而提升齿面微观形貌的粗糙度。

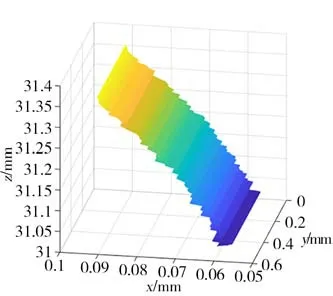
图7 齿面齿廓形貌仿真图Fig.7 The simulation profile of tooth surface

图8 不同砂轮转速下仿真与实验粗糙度对比图Fig.8 Simulation and experimental roughness at different grinding wheel speeds

图9 不同进给速度下仿真与实验粗糙度对比图Fig.9 Simulation and experimental roughness at different feed rates

通过对比实验与仿真的结果（表2），发现在进给速度较低的情况下，误差最大值为11.338%，产生误差的主要原可能有磨粒切削挤压工件，导致表面材料发生塑性变形；砂轮的修整水平；在低速情况下机床振动也会影响齿面微观形貌仿真粗糙度的准确性。正是这些因素在建模过程中未有考虑，导致了仿真结果与实验结果在某些数据结点存在较大出入，会对本次广义分析的理论建模产生影响。

3.2 曲面磨削微观形貌建模方法应用实例二

以轴承内套磨削为例，其磨削的工作原理如图10所示，在CBN砂轮工作的过程中，轴承内套与砂轮内切且两者按同方向自转，同时砂轮由机床控制来回进给，在两者相互配合下，生成砂轮磨粒的包络切削轨迹。轴承内套中心坐标系O1-x1y1z1通过自身转动和x方向上的进给得到轴承内套进给坐标系Of-xfyfzf，其中转角φ表示的是内圆弧转角，内圆弧线方程为：

图10 轴承内套磨削坐标变换示意图Fig.10 Coordinate transformation for bearing inner sleeve grinding

由于轴承内套在磨削过程中是以中心轴为基准做自转运动，因此式（21）中的φ可以利用轴承内套角速度ω和时间t对下式进行表达：

CBN砂轮与轴承内套各自的旋转中心处在同一垂直面上，因此Mf2中的y轴移动值为零。并且，在建立仿真过程中将砂轮的进给运动转换到工件上的进给运动，因此M22′为齐次单位矩阵。有所不同的是，此次砂轮是以x轴作为旋转主轴，因此需对M2s做出修改。

根据图10 及上述原理分析，结合方程组（13）可得关于砂轮不规则单颗磨粒相对于轴承内套磨削的三维轨迹方程组：

建立轴承内套实验来验证所建立预测模型的有效性，利用3MZ206DZ-CNC 全自动球轴承内圈内孔磨床对GCr15 轴承内套进行磨削实验，并利用VHX-500FE 超景深三维显微镜、Marsurf M300 粗糙度测量仪对工件表面三维形貌进行测量，其中实验参数如表3中所示。

表3 轴承内套磨削实验参数表Tab.3 Bearing sleeve grinding experiment parameter table

采用与实验相同的工艺参数，得到仿真形貌如图11所示。不同工件转速及不同进给速度下表面粗糙度的实验与仿真结果对比如表4所示，与上文中解释原理一致，当机床主轴转速减少或工件进给速率减少时，单位时间内轴承内套表面作用磨粒数量减少，导致曲面光滑程度会明显下降。

表4 关于轴承内套形貌仿真与实验粗糙度对比表Tab.4 Comparison table of simulation and experimental roughness of bearing inner sleeve appearance

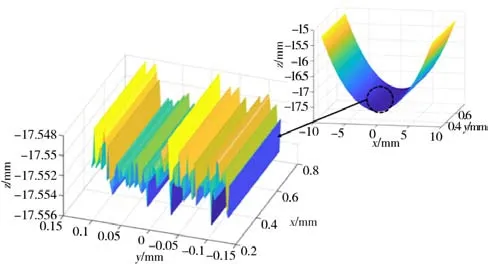
图11 轴承内套形貌仿真图Fig.11 Simulation diagram of bearing inner sleeve appearance

由表4 可知，仿真结果与实验结果是比较接近的，误差最大值为18.91%，由此可进一步验证本文所建立的曲面磨削表面微观形貌的建模方法是具有科学性和正确性的。

4 结论

（1）基于曲面磨削加工原理，建立砂轮坐标系与曲面零件坐标系之间的齐次变换矩阵，获得磨粒的三维运动轨迹方程，通过提出曲面区域逼近求解算法，解决加工过程中多颗磨粒轨迹相互交叉干涉的问题，建立一种适用于任意曲面磨削的表面微观形貌预测模型。

（2）以齿轮展成法磨削和轴承内套磨削为例，对所提出的曲面磨削工件表面微观形貌的建模方法进行验证。针对不同实验下，对比了各自正交实验参数下的仿真结果与实验结果的表面粗糙度值。结果表明，两类实验对象的表面粗糙度的最大误差分别为11.338%和18.91%，验证了仿真模型的通用性与有效性。

（3）该模型的建立可应用到研究空间曲面工件，如齿轮、凸轮轴等零件的表面磨削上，更加直观地反映曲面零件表面粗糙度与加工工艺参数之间的关联规律。