基于多源IMU和粒子滤波优化的姿态融合算法

宗意凯,苏淑靖,高瑜宏

(中北大学,省部共建动态测试技术国家重点实验室,山西太原 030051)

0 引言

姿态解算系统[1-2]广泛应用于无人机、自主机器人[3]、航空航天等强烈需求自身姿态信息的自动化系统中。随着近年来无人机[4-6]行业的发展,对微型航姿参考系统(AHRS)的精度要求进一步提高。受限于微机电系统(MEMS)的成本和尺寸限制,低成本惯性测量单元(IMU)方案存在较大的噪声误差和漂移误差,使得仅用陀螺仪解算得到姿态角具有明显的解算漂移[7-8]。针对低成本IMU传感器的误差问题,文献[9]基于自回归滑动平均系统设计了一套零滞后补偿的测量方法并实现了一种自适应滤波方法以降低噪声,但由于自协方差的求解不能保证无偏,因而对自协方差的反复迭代存在增大自协方差误差风险。文献[10]以样本长度、模型参数、降低模型阶数等方面为基础设计了一种随机误差补偿方法以优化Kalman滤波器[11-12]输出,但所建立的模型在预测误差较大时去噪效果不明显。目前主要使用互补滤波法、梯度下降法、卡尔曼滤波法实现姿态解算,其中互补滤波因其简化的计算量而被广泛用于嵌入式设备中。

互补滤波基于陀螺仪积分得到的角度,利用加速度计绝对静态下重力指向的唯一性对陀螺仪解算得到的姿态角进行收敛补偿。传统互补滤波模型利用单种六轴惯性传感器或九轴惯性传感器进行姿态解算,受所选惯性传感器噪声特性、漂移特性的影响。例如,BMI088六轴惯性传感器具有良好的零漂特性与温漂特性,但传感器数据存在较高噪声;ICM20689六轴惯性传感器具有较低的噪声特性,但其却存在较严重的零漂与温漂问题。此外,受限于MEMS传感器工艺限制,低成本IMU传感器的数据输出频率通常不高于1 000 Hz,使得陀螺仪的积分误差较大。基于以上两点,本文设计的IMU载板由BMI088与ICM20689组成,基于TMS320F28379S微处理器实现数据的采集与传输。以互补滤波算法为基础,发挥互补滤波传感器噪声频段互补的优势的同时结合粒子滤波处理非线性问题的优点,优化多源IMU数据融合补偿过程,从而更快、更准获取测量系统的姿态信息。

1 数据预处理

因数据采集平台与转台之间存在安装误差,需要对数据采集平台获取的六轴数据进行校准以消除坐标偏移误差对姿态解算的影响。因数据采集系统与转台系统分属2个独立系统,两者采集所得数据存在时间轴不对齐问题,需对两者时间数据进行对齐校正并裁剪多余数据以供结果分析。

1.1 传感器参数校准

由于数据采集平台坐标系与转台坐标系存在一定的安装误差,在解算姿态前需要计算校准参数以修正漂移误差和旋转误差。

建立采集平台加速度真实值与测量值关系表达式:

(1)

式中:Ature为采集平台加速度计真实值;R为表征测量值向真实值旋转的3×3矩阵;Scalex、Scaley、Scalez为表征真实加速度向量与测量加速度向量之间的缩放尺度;Amx、Amy、Amz为加速度计测量值;offsetx、offsety、offsetz为加速度计测量值的零漂。

对式(1)进行简化得到:

(2)

式中:Coffx、Coffy、Coffz均为加速度计偏置。

将式(2)进一步转换为齐次标准型后转置带入六面参数得:

(3)

利用最小二乘法求解式(3)方程:

(4)

式中:C为式(3)中的4×3待定校准系数矩阵;Am为式(3)中的6×4加速度计六面参数矩阵;G为式(3)中的6×3加速度计六面真值参数矩阵。

对静置50 s的陀螺仪数据求平均得到陀螺仪零漂量以修正陀螺仪零漂偏置。

1.2 时间轴对齐

转台记录得到的角速度数据与陀螺仪采集得到的角速度数据存在一致性,但由于惯性传感器数据采集与转台数据采集由2个独立系统分别实现,两者之间存在采样时间点不重合的问题。

惯性传感器数据采集的时间由28379S定时器记录,精确到1 μs,转台数据采集时间间隔为1 ms。因此首先使用分段三次样条插值方法对惯性传感器数据进行1 ms等间隔时间插值,生成获取同为1 ms时间间隔的惯性传感器数据序列。

基于MSE理论通过对2条曲线进行均方误差计算以获取两者重合度,损失函数为

(5)

离散计算公式为

(6)

对滞后曲线逐次时移并计算均方误差,均方误差最小时的时移系数即数据滞后时间。即计算式(7)最小值:

(7)

假设f2(x)滞后于f1(x),当式(7)中均方误差最小时,τ即滞后时间,计算得到滞后时间后对曲线进行时间轴裁剪以完成时间轴对齐。

2 改进型互补滤波算法

姿态解算即横滚角φ、俯仰角θ、偏航角Ψ的求解,基于陀螺仪积分获取得到的姿态角信息具有较好的高频特性,但由于陀螺仪的数据采样及解算过程为离散过程,在积分的过程中不能避免积分误差。因而纯陀螺仪解算得到的姿态角信息将会随着时间推移产生较大的漂移。利用加速度计解算姿态角即利用重力加速度在运载体坐标系下的矢量来求解运载体的姿态信息,加速度计具有较好的低频特性,且不随时间产生漂移,但当运载体进行大幅度运动时,加速度计不能表征运载体的剧烈运动姿态。基于陀螺仪较好的高频特性与加速度计较好的低频特性,进行互补融合可以获取兼顾高频特性与低频特性的姿态解算算法。

受低成本MEMS惯性传感器限制,参与解算的传感器数据频率基本不高于1 000 Hz,且易受单种六轴传感器设计本身的噪声特性影响。为此,本文基于多源惯性传感器优化姿态解算算法,提高单位时间样本量的同时,削弱单种传感器芯片噪声特性对姿态解算的影响。

尽管有大量研究表明基于线性高斯模型搭建的Kalman滤波器具有最小方差与最小误差的最优性,但在运载体的实际运动过程中,传感器受外部环境影响,引入的噪声信息并不完全符合线性高斯模型,因此本文依据粒子滤波理论[13-14]对互补滤波进行优化处理,期望获得相比传统互补滤波更优的姿态解算算法。算法结构如图1所示。

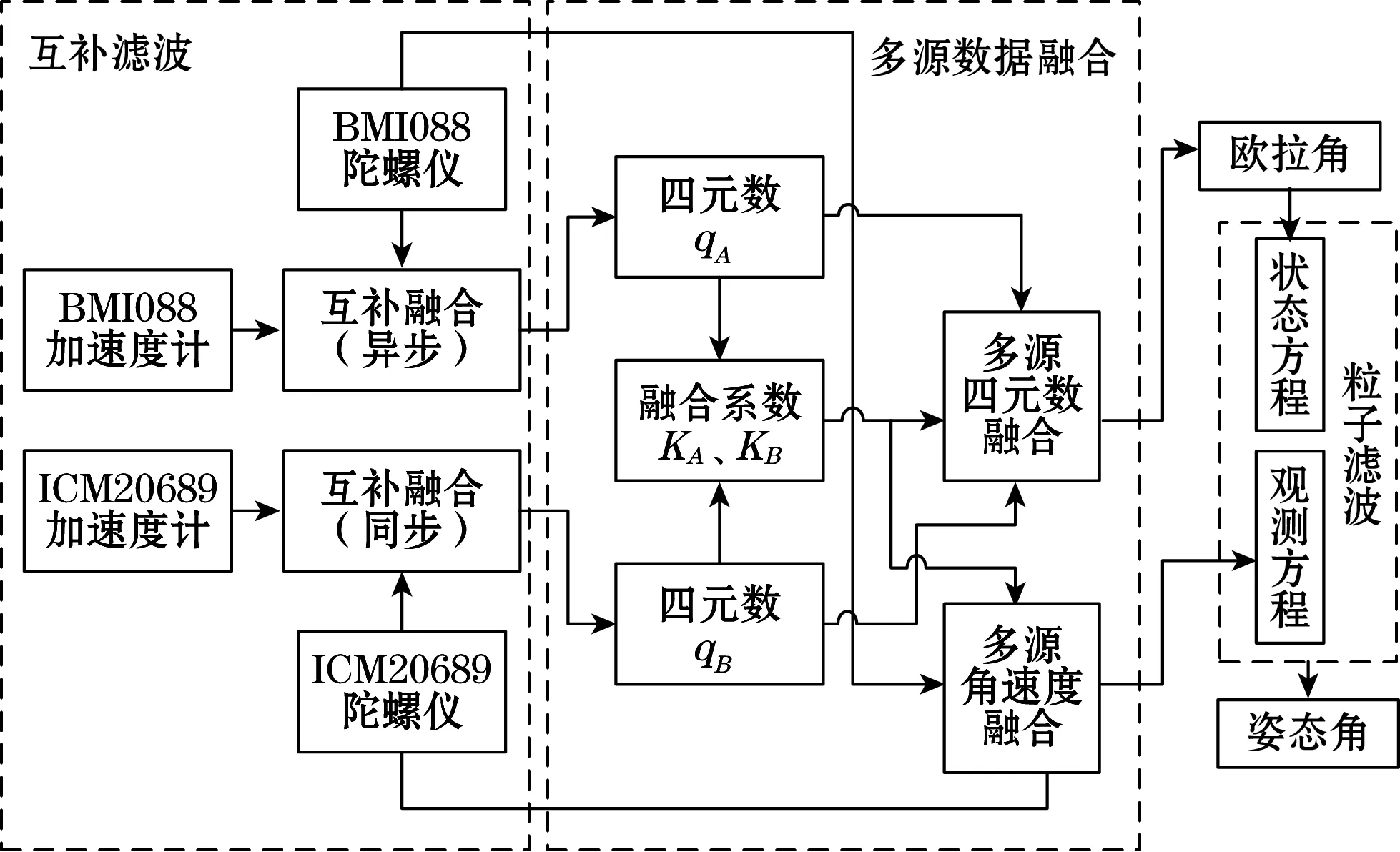
图1 姿态解算算法结构图

2.1 同步传感器互补滤波姿态四元数解算

定义四元数:

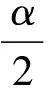
(8)

四元数q描述坐标系以[rxryrz]T为旋转轴,旋转α的过程。

基于上一次解算获取得到的姿态四元数估计重力方向向量:

(9)

对加速度计测得的重力向量与姿态四元数估计所得的重力向量做叉乘得到误差角的近似:

|am×a|=|am||a|sinθ

(10)

式中:am为加速度计测得的重力向量;a为姿态四元数估计所得的重力向量。

由于am与a均为单位向量,因此当运载体小角度运动时误差近似为

e=|am×a|=sinθ≈θ

(11)

误差角基于PI模型对陀螺仪测量所得角速度进行补偿得到修正后的角速度:

(12)

得到补偿后的三轴角速度后由四元数微分方程迭代更新四元数:

(13)

计算所得的四元数利用四元数定义可解算出三轴姿态角:

(14)

2.2 异步传感器角速度补偿优化

理想情况下,加速度计数据与陀螺仪数据的采样频率一致且采样同步,例如ICM20689六轴传感器在1 000 Hz采样率下加速度计与陀螺仪数据为同步采样。但BMI088六轴传感器加速度计最大采样频率为800 Hz,陀螺仪最大采样频率为1 000 Hz,加速度计数据与陀螺仪数据间存在较严重的异步现象,且两者采样时间间隔并不固定。为削弱BMI088加速度与陀螺仪异步采样数据对解算精度的影响,需对式(12)的角速度补偿公式进行优化。

利用DSP C2000的高精度捕获单元(eCAP)捕获BMI088加速度计与陀螺仪的数据就绪信号,计算得到陀螺仪数据与加速度数据之间的采样间隔时间τ。利用采样间隔时间τ动态修正式(12)角速度补偿公式中的比例项,优化后的角速度补偿公式为

(15)

式中:Tgyro为陀螺仪的采样周期;τ为陀螺仪数据与加速度数据之间的采样间隔时间;α为比例项下限系数。

当加速度数据采样离陀螺仪数据时间较远,则比例系数被相应减小,削弱加速度计数据对角度的修正。

2.3 多源姿态四元数融合

为融合多源传感器计算所得的四元数,建立多源姿态四元数融合公式:

qfusion=KAqA+KBqB

(16)

式中:qfusion为融合所得四元数;qA为基于ICM20689加速度计数据与陀螺仪数据进行同步传感器互补滤波姿态解算得到姿态四元数;qB为基于BMI088加速度计数据与陀螺仪数据进行异步传感器互补滤波姿态解算得到姿态四元数。

为削弱噪声特性对四元数解算的影响,利用信息熵对2种传感器的噪声进行评估,并基于评估调整2组四元数的融合权值KA、KB。

假定一段时间内的任一传感器四元数解算结果为q1,q2,…,qk,计算相邻时间的四元数偏差:

Δqi=|qi+1-qi|

(17)

得到k-1个偏差Δq1,Δq2,…,Δqk-1后对偏差数据进行量化编码处理:

ei=[Δqi/u]

(18)

式中u为编码步长。

利用k-1个量化编码计算概率:

(19)

式中c(ej)为编码ej出现的次数。

根据编码概率计算四元数的信息熵:

(20)

式中:m为c(ej)所有取值可能的总数。

信息熵H(q)越大则数据不确定度越大,噪声越大。基于信息熵计算结果对预融合权值KA′、KB′进行动态更新:

(21)

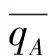
因此,融合四元数更倾向于当前数据,而根据他源四元数距当前的时间间隔动态削弱其融合权重。对四元数预融合系数归一化后得到四元数融合系数:

(22)

2.4 粒子滤波

建立状态方程与观测方程:

(23)

式中:Xk为k时刻的状态变量;Qk为k时刻的角度噪声;Yk为k时刻的观测值;Rk为k时刻的角速度噪声。

由于四元数本质为四维超向量,直接进行四元数粒子滤波计算量非常大,因此本文以欧拉角为基础构建粒子滤波模型:

(24)

(25)

生成n个粒子参与粒子滤波。由于粒子数量越多,计算量越大,因此为兼顾计算量,粒子数于100～500范围内选取。假设粒子服从的概率密度为

(26)

式中:ω(i)为粒子权重;δ(x)为狄拉克函数。

假设初始时刻x0的概率密度为

(27)

生成初始粒子并初始化粒子权重:

(28)

构建预测步计算公式:

(29)

(30)

(31)

(32)

构建更新步计算公式:

(33)

基于更新得到的概率分布计算期望得到姿态角结果:

(34)

(35)

2.5 重采样

在粒子滤波预测步更新过程中存在少数粒子占据极高权重,而多数粒子权重为0的现象。权重为0的粒子在后续粒子滤波过程中权重也将始终为0,该现象将使得实际参与粒子滤波的粒子数减少。为了削弱粒子退化引起的粒子滤波更新失效,当粒子群发生退化时引入重采样步骤,按概率对粒子进行复制与淘汰,权重高的粒子更有可能被多次复制,从而保证整个粒子群活性粒子的总数基本不变。

由于重采样会削弱粒子多样性,因此仅对明显退化的粒子群进行重采样。重采样触发阈值设计为

(36)

(37)

重采样序列示意图如图2所示。

图2 重采样序列示意图

取n次[0,1]范围内的随机数,根据随机数落点更新粒子:

(38)

并将所有更新后的粒子权重刷新为1/n:

(39)

3 实验数据处理及结果分析

3.1 实验平台

本文实验数据基于图3(a)所示三轴位置速率摇摆温控转台所得,数据采集平台实物如图3(b)所示。

(a)三轴位置速率摇摆转台

(b)数据采集平台实物

转台常温连续运行模式下三轴位置精度3″,回转精度3″,垂直精度5″;内框角加速度最大值2 000 (°)/s2,中框角加速度最大值1 000 (°)s/2,精度满足实验要求。转台记录三轴角度数据与角速度数据,数据间隔1 ms。

设定转台内框(横滚轴)和中框(俯仰轴)为摇摆组态并记录双轴摇摆实验下的角度与角速度。

3.2 数据采集平台硬件简述

数据采集平台硬件如图4所示。

图4 数据采集平台硬件框图

基于TM320F28379S微处理器设计数据采集平台。加速度计数据与陀螺仪数据基于SPI通信实时获取。

3.3 传感器参数校准处理及结果分析

基于传感器参数校准方法对BMI088加速度计数据进行校准,校准前与校准后六面数据如表1、表2所示,校准结果显示通过六面校准模型整定后六面数据的漂移误差与旋转误差均得到有效抑制。

表1 BMI088加速度计校准前六面数据 m/s2

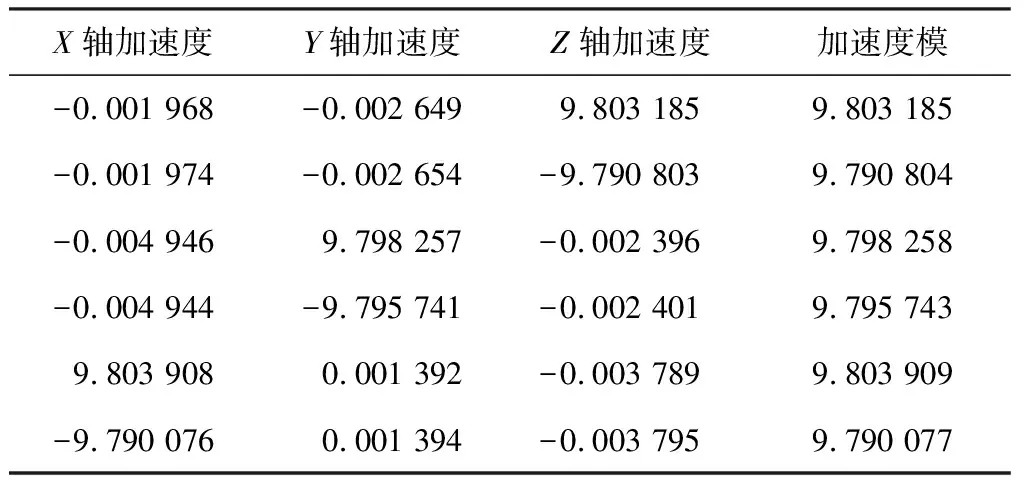
表2 BMI088加速度计校准后六面数据 m/s2

3.4 时间轴处理及结果分析

基于传感器数据与转台数据时间轴对齐方法对传感器数据与转台数据进行时间轴对齐与裁剪。时间轴对齐前与对齐后的角速度数据参考如图5、图6所示,结果显示利用该方法实现的时间轴对齐能够最大程度对齐2个独立系统的时间轴。

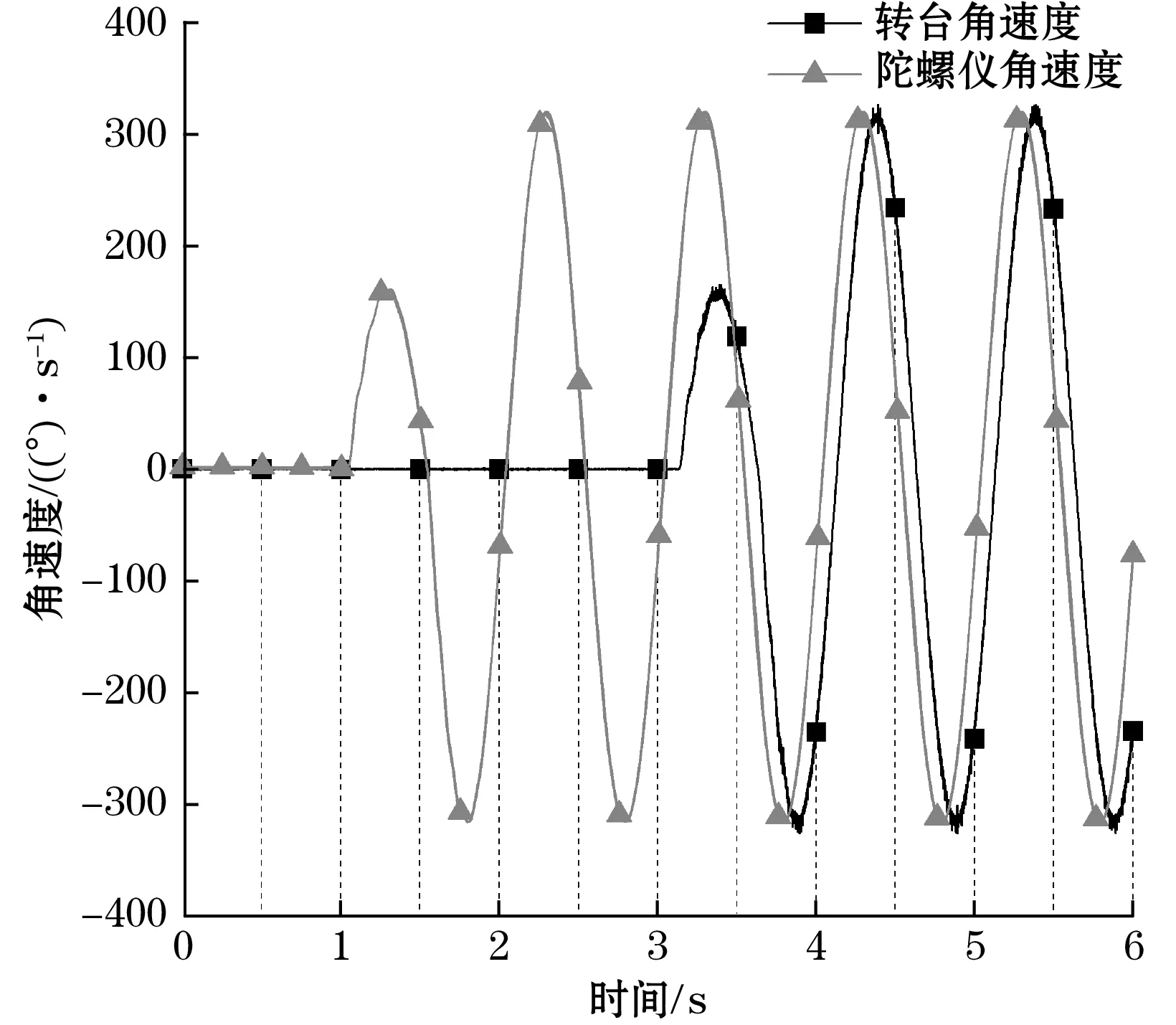
图5 时间轴对齐前角速度数据参考

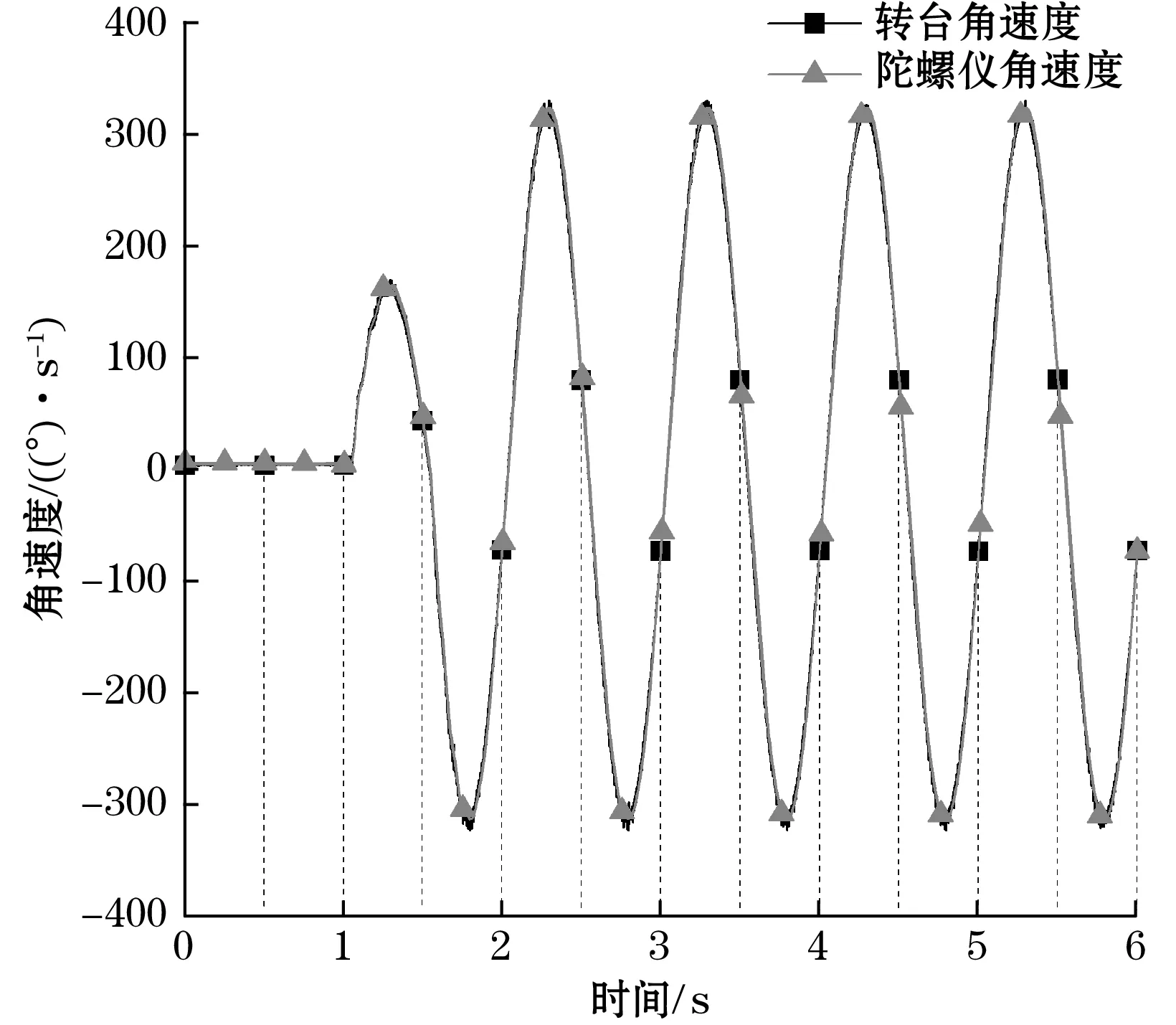
图6 时间轴对齐后角速度数据参考

3.5 姿态解算结果对比分析

本文以高精度转台记录得到的三轴实际角度作为真实角度信息对解算所得姿态角进行评估。对比不同方法下姿态解算结果。

对仅使用BMI088解算姿态、仅使用ICM20689解算姿态、使用BMI088+ICM20689解算姿态、使用BMI088 +ICM20689基于粒子滤波优化解算姿态进行测试对比。计算各姿态解算方法得到的俯仰角、横滚角解算角曲线与转台记录的实际姿态角曲线间的均方误差;记录23 s后无磁力计参与计算的解算漂移误差角;计算解算角曲线与实际姿态角曲线的时间迟滞。利用上述3项指标对各姿态解算方法进行评估。

仅使用BMI088六轴传感器解算所得姿态角如图7～图9所示,图中深色曲线为转台记录所得的实际角度曲线,浅色曲线为解算所得角度曲线。由对比结果可见,基于BMI088低零漂特性,在摇摆实验下姿态角解算零漂较低,而由于未引入磁力计以修正偏航角漂移,姿态迭代23 s后产生了-3.051 2°的漂移。

仅使用ICM20689六轴传感器解算所得姿态角曲线与实际角度曲线如图10～图12所示。由对比结果可见,由于ICM20689相对较差的零漂特性,在摇摆实验下横滚角解算表现出明显的零漂现象,而由于未引入磁力计以修正偏航角漂移,姿态迭代23 s后产生了-3.795 1°的漂移。

使用BMI088+ICM20689多源传感器组合基于粒子滤波优化解算所得姿态角如图13～图15所示。由对比结果可见,利用2颗非同种IMU进行姿态解算,在摇摆实验下解算结果得到明显改善,解算角度曲线与实际角度拟合度明显提升,而23 s后偏航角解算漂移也被抑制至-0.848 2°。

各方法解算所得姿态角与转台实际角度之间的均方误差、偏航角解算漂移和解算时滞如表3所示,序号1为仅使用BMI088进行姿态解算结果;序号2为仅使用ICM20689进行姿态解算结果;序号3为使用BMI088和ICM20689进行姿态解算结果;序号4为使用BMI088和ICM20689并利用粒子滤波优化实现的姿态解算结果。通过实验数据对比可以看到,引入多源传感器组合进行姿态角冗余计算明显缩减了姿态解算的滞后时间并提升了俯仰角与横滚角的解算精确度。基于粒子滤波优化后的互补滤波姿态解算方法进一步提升了俯仰角与横滚角的解算精确度。在未使用磁力计参与解算的条件下偏航角的解算存在漂移,但通过实验数据可以发现引入多源IMU对偏航角的漂移有着明显抑制作用。

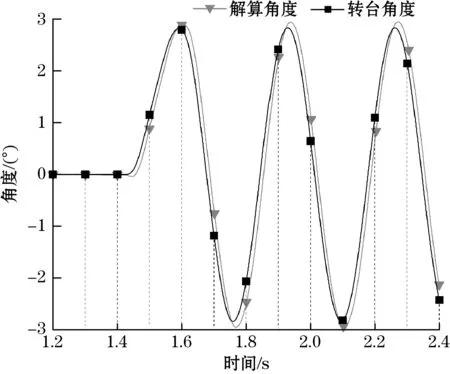
图7 纯BMI088互补滤波俯仰角解算结果图

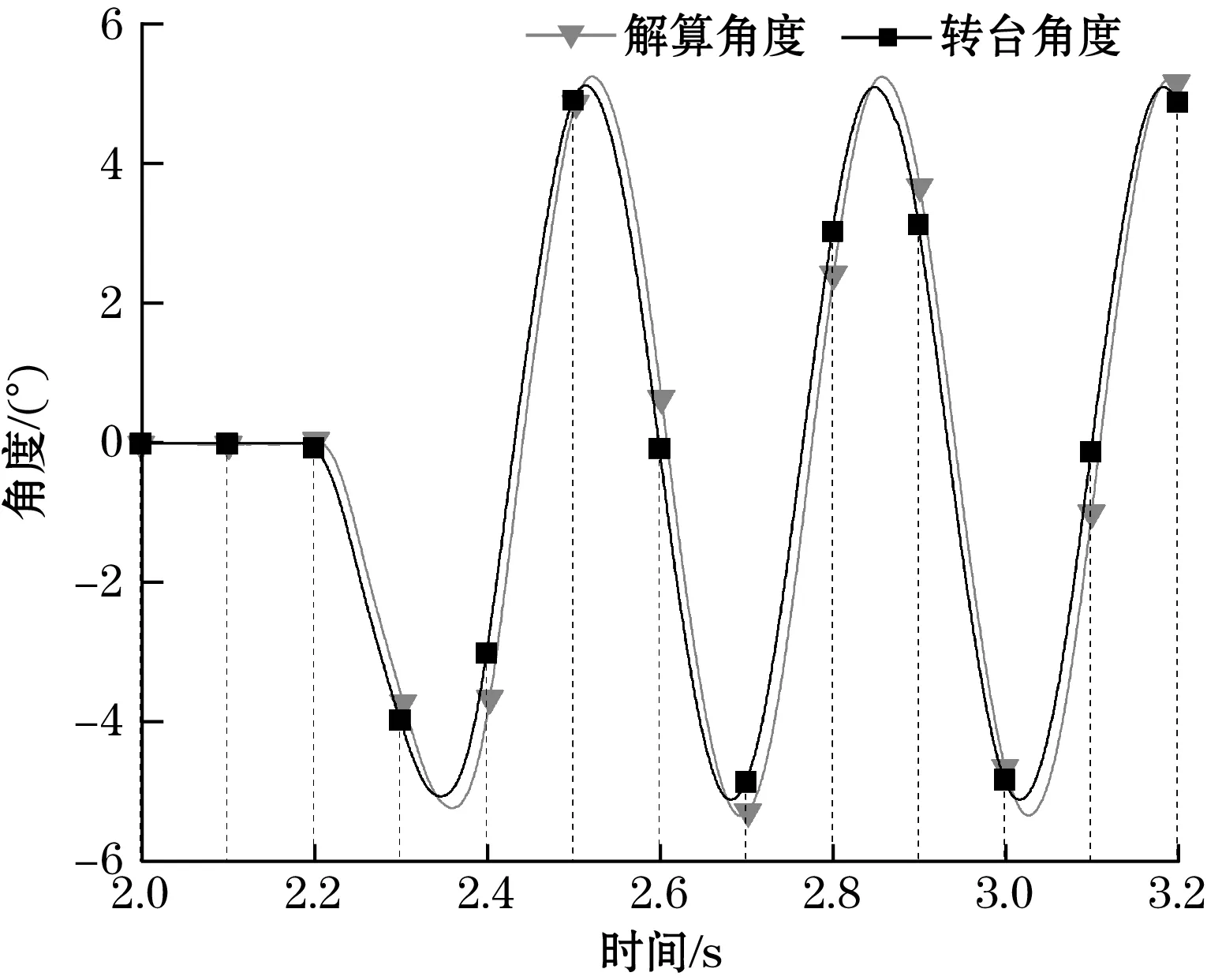
图8 纯BMI088互补滤波横滚角解算结果图

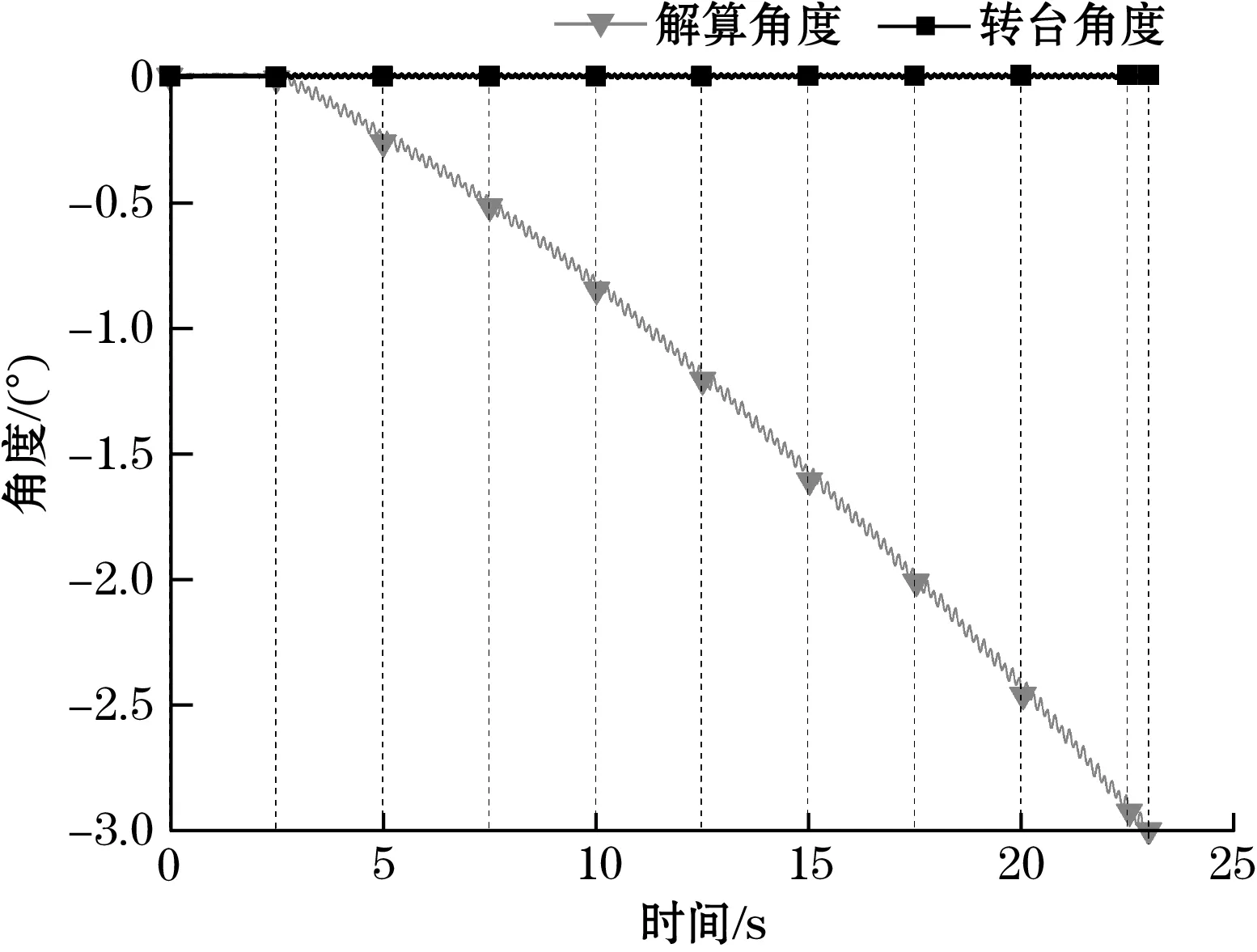
图9 纯BMI088互补滤波偏航角解算结果图

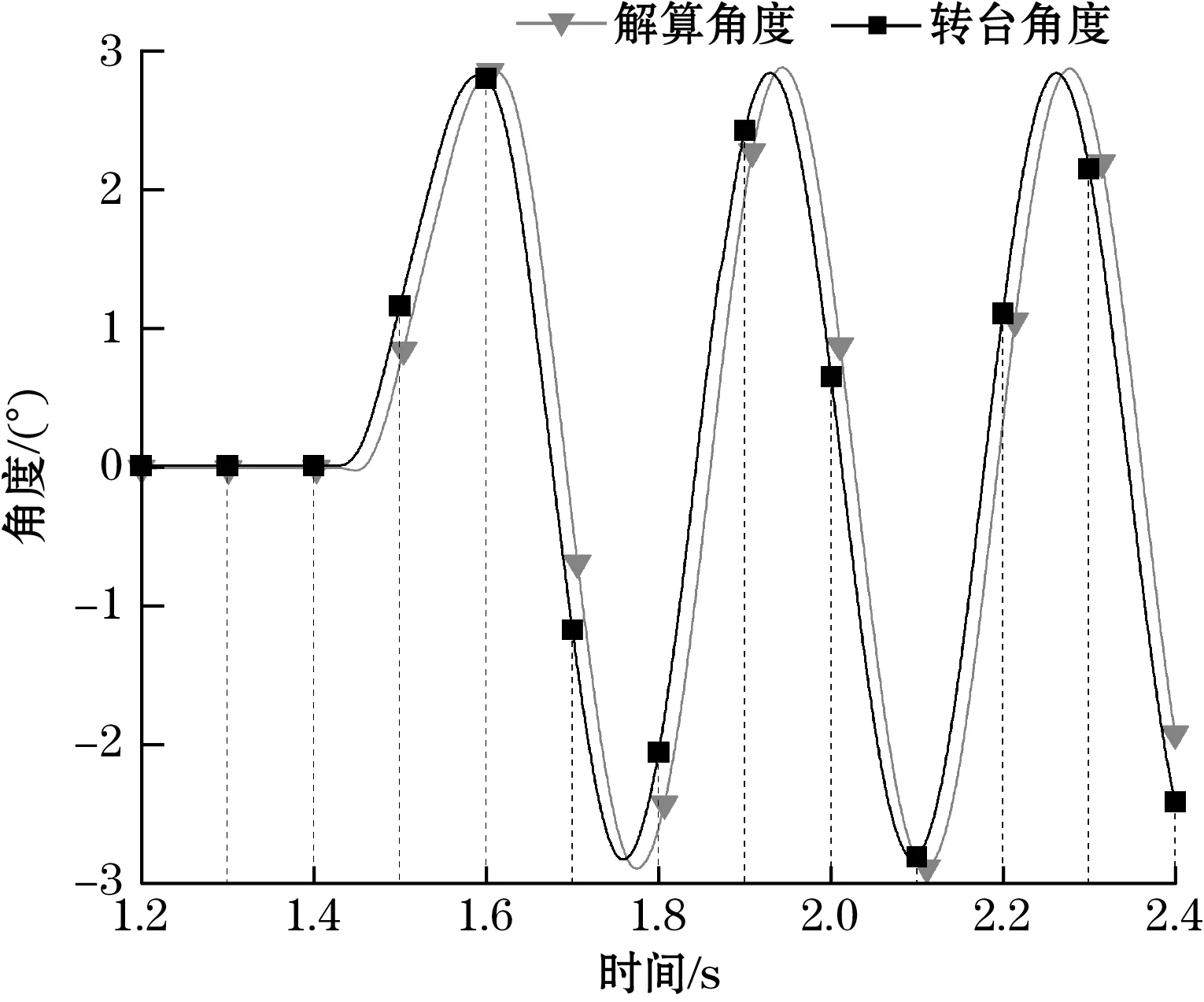
图10 纯ICM20689互补滤波俯仰角解算结果图

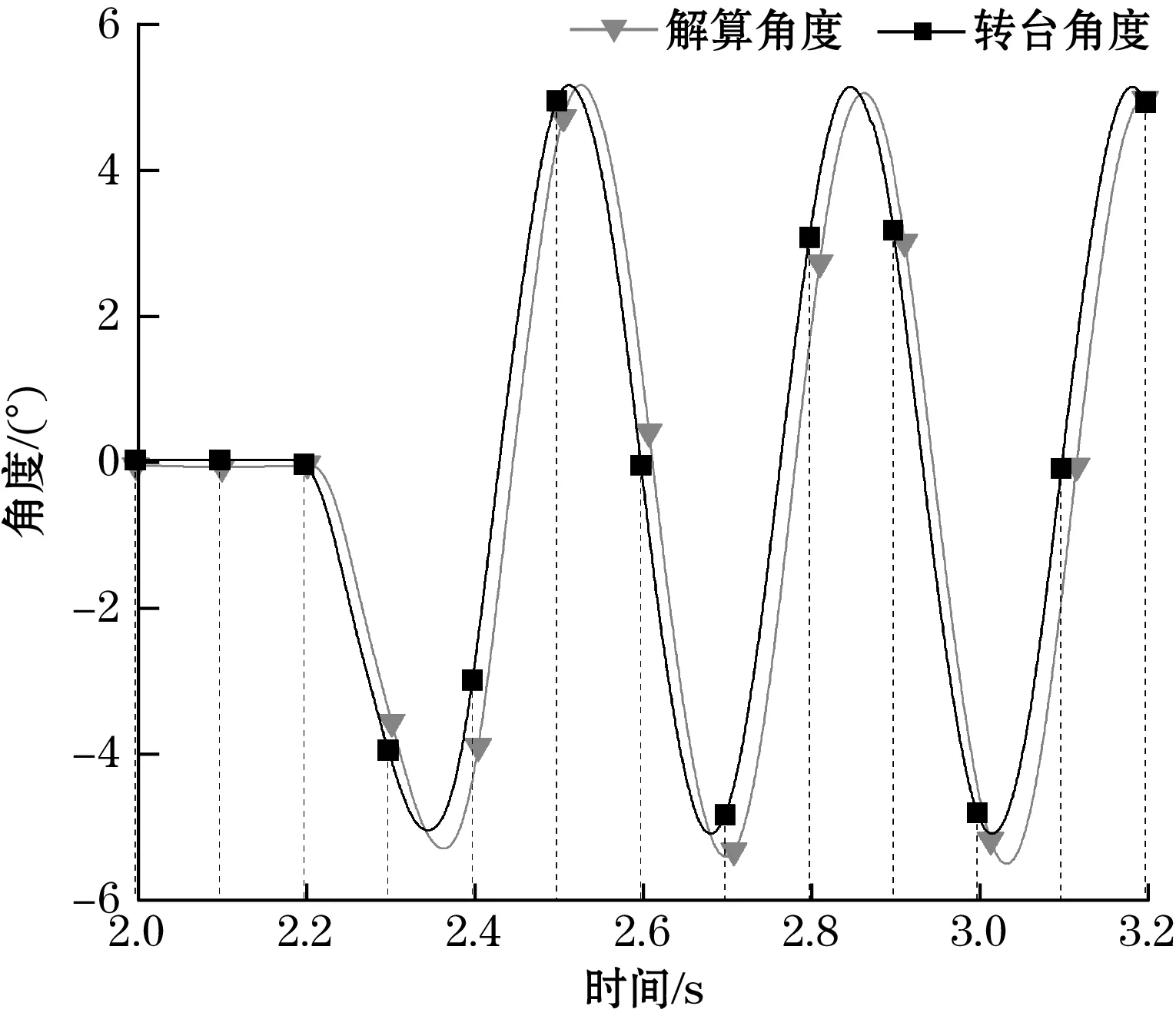
图11 纯ICM20689互补滤波横滚角解算结果图

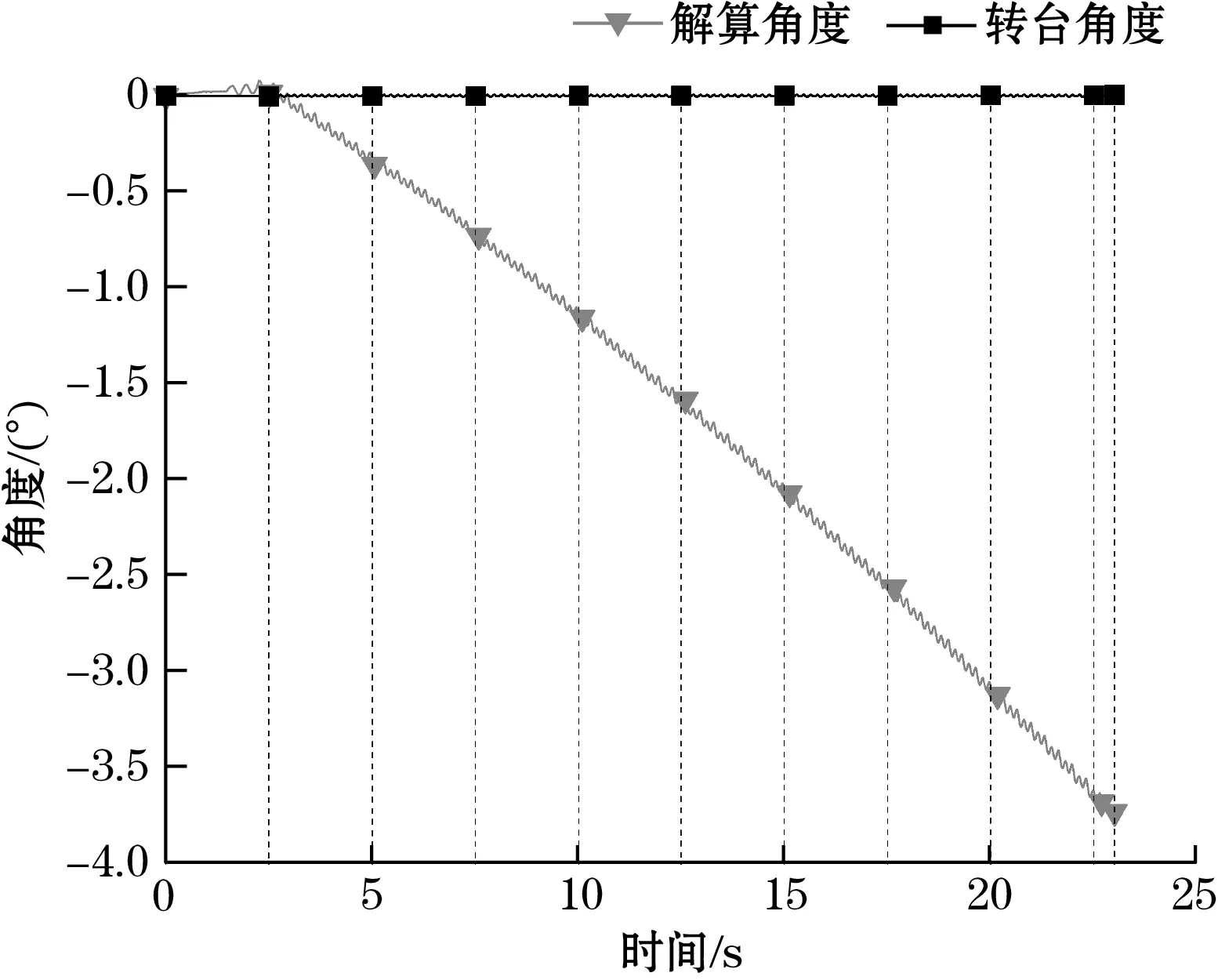
图12 纯ICM20689互补滤波偏航角解算结果图

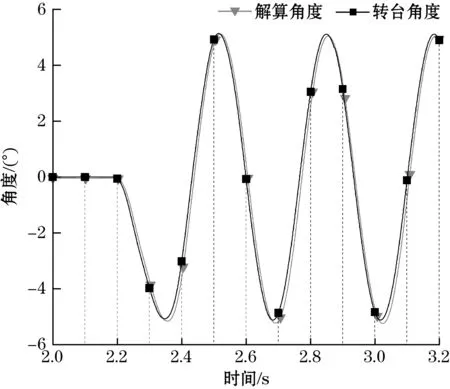
图14 改进型互补滤波横滚角解算结果图

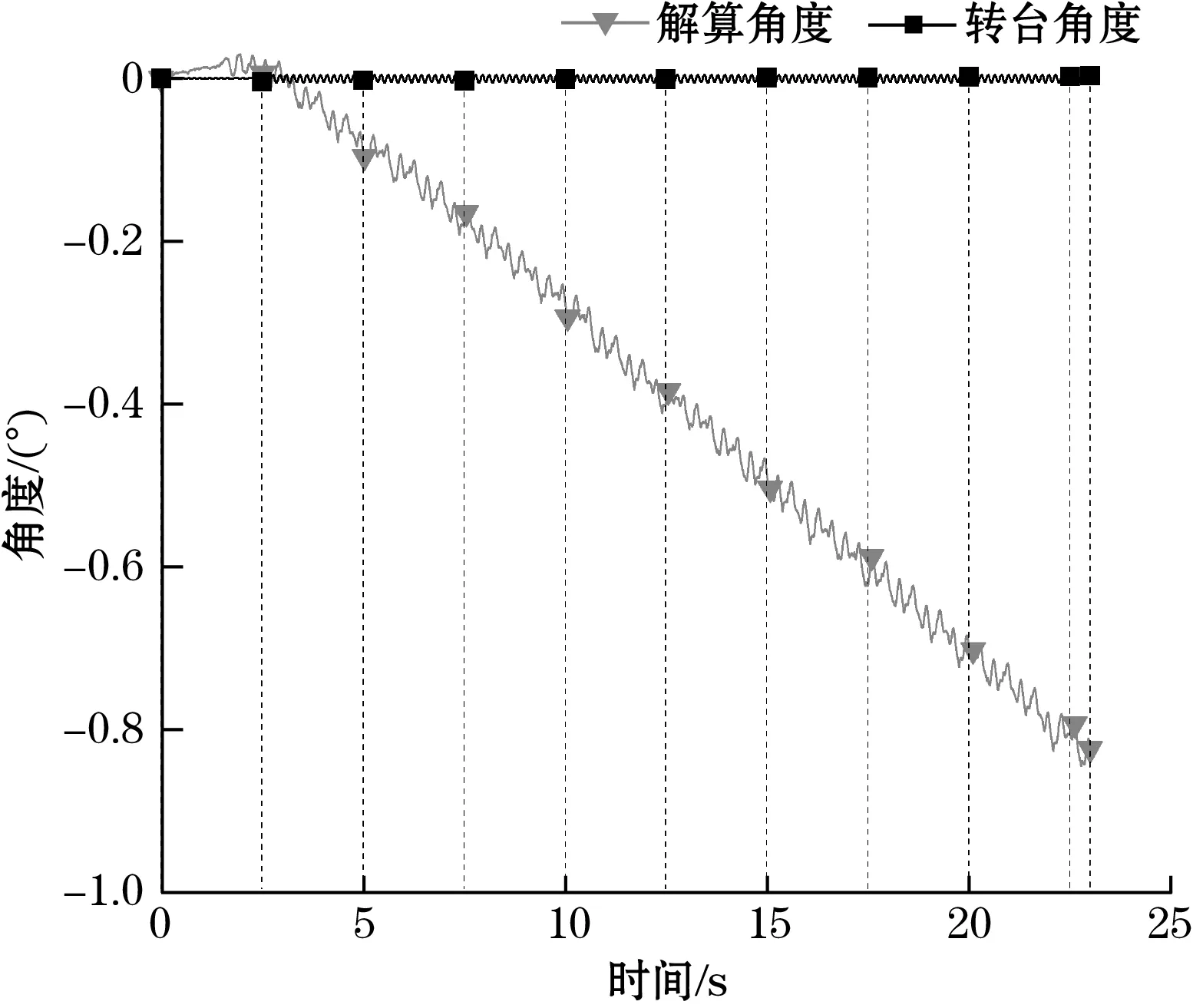
图15 改进型互补滤波偏航角解算结果图

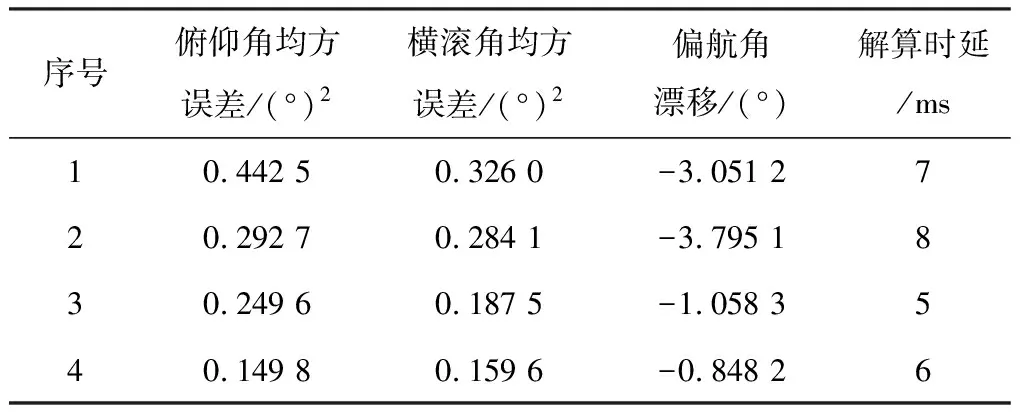
表3 解算结果误差及时延对比

4 结论

本文针对互补滤波姿态解算算法引入多源传感器组合与粒子滤波方法以实现对姿态角解算的优化。基于高精度转台记录所得角度数据对解算角进行验证分析,结果表明该设计的改进型互补滤波方法对姿态解算的精度有较高的提升,对无磁力计参与解算下的偏航角偏移有着明显抑制。在本设计基础上可继续引入与ICM20689对称分布的ICM20602六轴传感器参与冗余解算以消除ICM20689相对BMI088位置的中心偏移影响,引入磁力计数据以约束偏航角的解算漂移[15-16],获得更优的姿态解算方案。