基于局部优化的图表示学习增强

唐正正 汪 洋 洪学海,3 班 艳 姚铁锤 乔子越

1（中国科学院计算机网络信息中心信息化发展战略与评估中心 北京 100190）

2（中国科学院大学计算机科学与技术学院 北京 100049）

3（中国科学院计算技术研究所信息技术战略研究中心 北京 100190）

（tangzhengzheng@cnic.cn）

网络（图）是日常生活和学术研究中广泛存在的一种数据类型，如数据库系统和逻辑编程（database systems and logic programming，DBLP）中的引文网络[1]、微博用户间的社交网络和城市运输的交通网络等.由于网络是非常重要的信息载体和表现形式，相关网络应用算法不断被提出，包括节点分类[2-4]、链接预测[5-7]、社区发现[8-10]和分子性质预测[11-12]等.各类算法中，网络表示学习（network representation learning，NRL）近年来受到了广泛的关注，它的目标是学习网络节点的分布式实值表示.具体来说，NRL 通过解决一个优化目标将图G中的每个节点v映射到一个潜在的d维向量空间，在低维表示中捕获邻接相似性和社区成员.学习到的节点表示还可以作为下游机器学习任务的初始特征.由于图表示学习的简单、高效和可扩展性，使得大规模网络上的机器学习成为可能[13].

网络表示学习通常需要将节点的上下文信息（即与它相连的邻近节点信息）嵌入到节点表示中，然后通过最小化任一节点“生成”上下文节点的条件概率来学习节点的表示，最终使得节点与其上下文节点之间的表示在低维空间上的距离接近[13].然而，近年来的一些研究表明，由于上下文噪声（类间边）的存在使得图表示学习在训练过程中会不断地将噪声信息融入节点最终表示，这导致不同类节点在表示空间难以区分，不利于下游网络任务的分析[14].

用于机器学习的图数据一般包括拓扑结构和节点属性2 种特征.研究者试图通过原始图特征降低网络内部的噪声边比例，同时增加类内边的比例.这会提高各类图表示算法的表示效果或者是在模型训练中减缓噪声边的影响.最近有3 类相关研究策略被提出：1）每一次训练之前随机删除拓扑结构中的部分边[15-16]；2）通过节点特征预训练一个链接概率矩阵，基于连接概率矩阵增删节点边[17]；3）在算法训练过程中通过特征相似性进行边筛选[18].这些方法都使用了节点属性信息，但无法应用到无特征网络中.

本文针对无特征网络设计了一组噪声边优化策略.通过优化策略可以删除网络中的噪声边，增加网络中的类间边，达到网络表示学习的增强效果.本文从相关理论证明了优化策略的合理性，并在6 个公开图数据集上进行节点分类、链接预测和社区发现任务实验.实验显示，经过优化后的多个NRL 方法在3 个任务中的效果均有显著增强，验证了本文策略的有效性.本文最后还进行了超参敏感性分析，以验证优化策略具有较好的鲁棒性.

1 相关工作

图表示学习能够将图数据转化成低维稠密的向量化表示的方法有3 种，下面详细介绍.

1）图表示学习.较早的图表示学习方法基于线性或非线性降维技术，经典的算法有LLE（locally linear embedding）[19]，LE（Laplacian eigenmap）[20]，SC（spectral clustering）[21]等.这些方法的共性是都需要对特定的关系矩阵进行特征向量求解.例如SC 通过计算关系矩阵的前k个特征向量或奇异向量得到k维的节点表示，其中关系矩阵一般是网络的邻接矩阵或者拉普拉斯矩阵.这类方法对于关系矩阵十分敏感，不同关系矩阵的评测结果差异很大[22].另外关系矩阵只包括1 阶邻接关系，对于大型网络来说一般是稀疏的，通过降维分解后的表示往往不足以表达网络结构[23].

针对这一问题，GraRep 算法[24]通过结合多阶邻接信息来增强网络的表示效果，它将初始邻接矩阵A进行行归一化处理，行元素的值表示对应节点之间的1 阶转移概率.通过对不同阶矩阵Ak归一化处理表示对应节点之间的k阶转移概率，最后将不同阶矩阵分解得到的特征拼接组成维度更高、表达能力更强的节点表示.具体融合多阶邻接信息的矩阵M构建形式如式（1）：

虽然GraRep 表示性能得到很大提升，但与早期基于矩阵分解的方法一样，都具有复杂度高和计算耗时等缺陷，难以扩展到大型网络的表示学习[22].DeepWalk 算法[25]将深度学习思想引入网络表示学习，它通过在网络中进行截断随机游走生成节点序列，然后使用NLP 领域中广泛使用的Word2vec 思想，结合Skip-gram 的训练方法，得到每个节点的嵌入表示.Node2vec[26]进一步扩展了DeepWalk 算法，它通过设置2 个超参p，q分别控制游走的方向，可以做到广度优先搜索和深度优先搜索的随机游走.DeepWalk 算法也用到了高阶邻接信息，融合多阶邻接信息的矩阵M构建形式如式（2）：

其中w表示随机游走序列中的滑动窗口大小，在实际模型训练中w表示实际可到达的最高阶邻居.

除了上述基于序列的图嵌入方法外，研究者还探索将文本、标签等元信息纳入NRL 算法.TADW[27]在矩阵分解框架下考虑文本信息，MMDW[28]联合优化最大边际分类器和社区结构表征学习模型，学习到的表征不仅包含网络结构，而且具有区分性.作为另一种半监督NRL 方法，GCN[29]和DDRW[30]被提出用于半监督图表示学习.SDNE[5]采用深度神经模型进行图表示学习.LINE[31]对顶点之间的1 阶和2 阶邻接性进行建模，用于学习大规模网络嵌入.

2）网络降噪.由于网络噪声的存在，导致很多图表示学习在训练的过程中会出现过度平滑的现象[32].为了缓解网络噪声的影响，ResGCN[33]提出了一个图的残差学习框架，通过引入输入层和输出层之间的残差连接（residual connection）大大缓解了过度平滑的问题.DropEdge[34]通过从输入图中随机删除一些边，可以缓解过度平滑的影响.这2 种方法原则上延缓了过度平滑的出现，却没有添加新连接边并从中获益.ADAEDGE[17]使用类似去噪和预滤波的方法，在训练迭代过程中根据预测，在具有相同（不同）标签的节点之间添加（删除）连接，并具有较高的置信度.同样，BGCN[18]迭代训练一个具有GCN 预测的同型混合隶属度随机块模型，产生多个去噪图，并由多个结果融合集成最终的表示.GAUG[35]通过预训练一个连接概率矩阵，然后生成多个结构图，通过多种边连接组合共同学习网络表示.以上降噪工作都是针对特征网络进行研究提出的相关算法，无法适用于无特征网络，由于无特征网络的可用初始特征较少，通过简单随机的删除边可能会导致孤立节点的情况，优化效果往往适得其反.

3）随机游走.随机游走方法在网络任务分析中是一种常用的技术手段.在节点嵌入算法中，DeepWalk[25]是近几年最有影响力的方法.其主要思想是利用随机游走对图中的节点进行采样，然后将节点之间的共现关系作为训练样本输入Word2vec 中，学习节点的向量表示.Node2vec[27]在DeepWalk 的基础上更进一步，它通过调整随机游走的权重，使得图嵌入结果在同质性和结构等价性之间进行权衡.SSDW[36]考虑到传统网络嵌入模型在随机游走序列采样过程中是无监督的，采用成对约束来指导随机游走过程中的节点转移概率.在预先获得先验信息的情况下，如果下一个节点与当前节点属于同一个社区，则下一个节点的抽样概率要增大；否则，应降低下一个节点的抽样概率.另外，在社区发现算法中，Sharma 等人[37]提出的引入基于光谱偏置随机游走的节点嵌入来源于对访问节点周围邻域结构的感知.Zhang 等人[38]提出了一种基于有限随机行走步数的层次团体检测方法，利用核心节点的局部近似收敛而不是概率转移矩阵的全局平滑收敛.Pons 等人[39]定义了顶点之间和顶点集之间的距离度量，这些度量有效捕获了网络中的社区结构.距离是根据随机步行者在固定的步数中从一个顶点移动到另一个顶点的概率计算出来的；然后利用凝聚层次聚类技术对顶点进行分组.Fu 等人[40]根据一些社会原则提出了一种基于阈值随机步行者的可扩展社区检测方法（CD-TRandwalk），该方法使用随机游走技术将有许多共同邻居的顶点聚类到同一个社区.

2 预备工作

本节首先对研究问题做出定义及相关符号说明.然后，展示了网络噪声如何影响本文的研究.为了能够提出合理的降低策略，本文对节点局部邻接分布进行了假设研究.最后基于该假设，给出本文的研究动机，并证明该动机的合理性.

2.1 基本定义

2.2 节点对噪声的敏感性

对于任意节点vi，我们定义了一个测量值，命名为边纯度（purity of edge，PE），记为Pe.Pe（i）值的大小反映了节点vi的 1 阶邻居中与节点vi同标签的比例，具体定义为：

其中Pe（i）∈[0,1],N(i) 表示节点vi的 1 阶邻居集合.Li,Lj分别表示节点vi,vj的 类别标签，⊕表示与或操作.

从直觉上看节点vi对 应的Pe（i）值越大，该节点经过图表示学习后被正确分类的概率应该也会越大.为了验证这个想法，我们在同一个公开数据集Wiki上分别使用DeepWalk，Node2vec，SNDE 这3 个图表示学习算法进行了10 次的分类预测，10 次训练设置完全相同，使用20%的数据量进行训练，表示维度设置为128，其他参数都使用算法默认值，然后统计余下全部节点在10 次分类任务中被正确预测的次数.

为了更好地进行可视化对比，本文统一使用DeepWalk 算法学习的表示进行可视化展示.图1（a）是根据节点PE 进行展示，图1（b）～（d）分别对应3种NRL 算法的预测结果.可以清晰地观察到，对于任意节点，Pe值越大，其在3 种算法中都会被多次甚至全部预测正确；反之，Pe值较小的节点在3 种NRL 算法中都较少，甚至没有一次被正确预测.图1（b）～（d）显示的预测结果分布与图1（a）Pe值分布保持一致.这佐证了我们的想法，通过Pe值可以直接了解节点周围噪声边的比例，如果Pe值较小，表明节点周围有更多的噪声边，在各种算法中，该节点的嵌入表示难以学习到有效的结构信息，分类的效果就会很差.

2.3 局部邻接的分布特性

很多图表示学习算法都对图进行了拉普拉斯正则化处理，这一处理在各种算法中都被验证给模型带了积极的效果.图拉普拉斯正则化被认为可以约束标签与图结构的一致性[41]，而这种处理方式建立在一个重要的假设-网络的局部同质性，即连接的2 个节点趋向于相似和具有相同的标签[32].基于这一网络特性我们做出假设1，并对该假设进行了论证.

假设1.由于网络的局部同质特性，任意节点在其2 阶邻居中发现同类节点的概率大于其在1 阶邻居中发现非同类节点的概率.

其中k+1为节点类别数目.令p2>q1化简得到kα3>αβ2+(k-1)β3，如果网络中只有2 类节点即k=1，不等式化简为 α>β，显然成立.证毕.

由于局部同质特性在节点任意连续的1 阶、2 阶邻居间具有传递性，例如节点vi的连续1 阶、2 阶邻居分别是vs,vf，而节点vs为 节点vf的1 阶邻居.所以对于k>1的 网络，只需要考虑节点vi及其连续的1 阶、2阶邻接节点.基于此，我们在真实数据集上通过随机游走的方式统计所有节点及其连续1 阶、2 阶邻接节点类别数目，具体情况如表1 所示.可以观察到，在k>1的网络中，由于局部同质特性，任意节点及其连续1 阶、2 阶邻接3 个节点之间类别互不相同（2 阶子图内k>1）的占比很少，即2 阶局部子图满足k≤1的情况占绝大部分，因此假设1 适用于大部分情况.

Table 1 Class Proportion Statistics for Any Node vi and Its Consecutive 1,2 Order Neighbors 表1 全网络任意节点v i及其连续1,2 阶邻居类别数占比统计 %

2.4 本文研究动机

由于图结构噪声的存在，各种NRL 算法在训练过程中融合学习了噪声信息，使得节点表示间的边界模糊，这阻碍了各种下游网络任务的分析（本文任务是节点分类）.通过拓扑优化处理，可以增强节点最终的表示效果.在最好的情况下，优化策略能够添加类内的（不存在的）链接，删除噪声边的（存在的）链接，可以生成一个网络Gidea，即只存在类内边连接的网络.

研究动机：给定一个理想网络Gidea，在图表示学习中添加高阶邻接信息，对于下游节点分类任务的作用将微不足道.考虑一个极端的场景，即所有可能的类内边都存在和所有可能的类间边都不存在.场景图可以看作是c个全连通的组件，c是节点类别数，每个组件中的节点具有相同的标签.在这种情况下，各种 NRL 方法在Gidea学习到的节点表示可以很容易地完成分类任务，具体理论证明如下：

证明.给定一个无向无权重网络G=(V,E)，然后需要对此网络的关系矩阵M进行分解，不同的NRL方法采用的矩阵类型虽然不同，但总的目标就是要找出2 个低维矩阵R∈R|V|×d,CT∈Rd×|V|，使得两者内积接近M.这一步通常使用最小化范数 ||M-R·CT||来实现.假设G包含c个全连通分量，则有块矩阵B：

其中Aii∈[1,c]表示某一社区内部的拓扑结构，c表示节点类别数，O表示对应维度零矩阵.

由于在理想图之间不存在类间边，并且邻接矩阵的高维构建也只对块矩阵操作，那么可以得到该网络对应的多阶邻接矩阵M：

用特征方程结合矩阵初等行变换方法求矩阵的特征向量.首先根据关系式Ax=λx可写出(λE-A)x=0，继而写出特征多项式 |λE-A|=0，具体形式为：

其中Ei是和Mi相 同维度的单位矩阵.可以直观地看到理想图情况下，针对多维邻接矩阵特征向量的求解过程，每个块矩阵是独立不相关的，最终求解得到的多个特征向量也只与块矩阵相关，对于降维后的节点表示F∈RN×d，形式为：

不同类节点的特征表示之间向量积都是零，完全独立不相关，对于分类任务显而易见.针对现实网络数据中的噪声连接，通过合理的降噪处理可以增加网络类内连接以及减少类间连接，能够减小噪声图与理想图之间的差距.

3 局部边优化处理

基于2.4 节的研究动机，本文提出“2 步骤”优化策略.首先，介绍了2 种用于计算节点之间邻接相似性的计算方法.然后，给出利用相似性计算方法结合节点度数对网络进行局部优化的策略.最后对优化策略进行逻辑梳理及复杂度分析.

3.1 邻接相似值计算

1）局部邻接相似计算.1 阶邻接相似是边连接的成对顶点之间的局部相似，一般计算方法有邻域重叠（neighborhood overlap，NO）、杰卡德系数（Jaccards’s coefficient，JC）、最小归一化重叠（minimum normalized overlap，MNO）、余弦相似度（cosine similarity，CS），具体计算如表2 所示.然而，由于网络的稀疏性，许多类内链接的缺失，1 阶邻接计算不足以表示节点之间的相似性.此外，NEU 算法[23]已经证明，在中心节点的局部子图内，距离中心节点越远的节点对于中心节点的影响越小.基于这种局部特性以及假设1，本文提出融合1 阶、2 阶邻接结构信息的相似计算策略.对于任意节点vi和节点vj之间的相似性Sij计算为：

Table 2 Similarity Calculation Methods表2 相似计算方法

2）多阶邻接相似计算.通过本文的研究工作发现，融合高阶邻接结构信息的NRL 算法生成的节点表示能够更准确表达出网络结构的真实情况.然而，由于计算复杂度比较高，在大规模网络中，精确计算高阶邻接Ak是低效的.为此，本文设计了另一种基于随机游走的多阶邻接矩阵Mmulti计算策略.具体的计算策略分为2 个步骤：首先以网络中的每一个节点vi为起点，进行w次长度为l的随机游走，产生对应节点vi的 邻近节点集Ne(i)，节点集大小等于w×l；然后遍历Ne(i) 每个节点vi，并将对应转移权重矩阵A∗的行向量全部累加，进行标准化之后的行向量可以近似该节点游走到l阶内任意邻近节点的概率.具体计算为：

A∗是 矫正之后的转移权重矩阵，表示以节点vi为起点随机游走任意一次到达节点vj的权重贡献.

DeepWalk，Node2vec 等基于序列的表示学习算法，通过对游走序列进行节点对采集，构造出一个集合，然后在集合中随机抽取节点对近似节点之间的相似值，但没有显式地保存各节点对之间的相似值.本文的方法可以显式计算并保存中心节点与多阶邻居内全部节点之间的相似值.

3.2 局部优化策略

在多个图表示学习算法中，一个重要的前提假设就是局部同质[42]，即相同标签的节点更容易建立边连接以及有连接边的2 个节点具有类似的特征信息.然而，在现实网络中，任意中心节点的局部邻接内，一般都存在不同类别的邻居.我们把这样的边称作噪声边.由于噪声边的存在，学习到的节点表示会融合噪声节点信息，这会增加下游如节点分类任务的难度.通过本文研究动机的理论证明可知，如果利用原始邻接信息，能够对网络结构进行优化预处理工作，理想情况如图2 所示.图表示学习方法在优化之后的网络结构中学习到的节点表示更容易被区分开来.

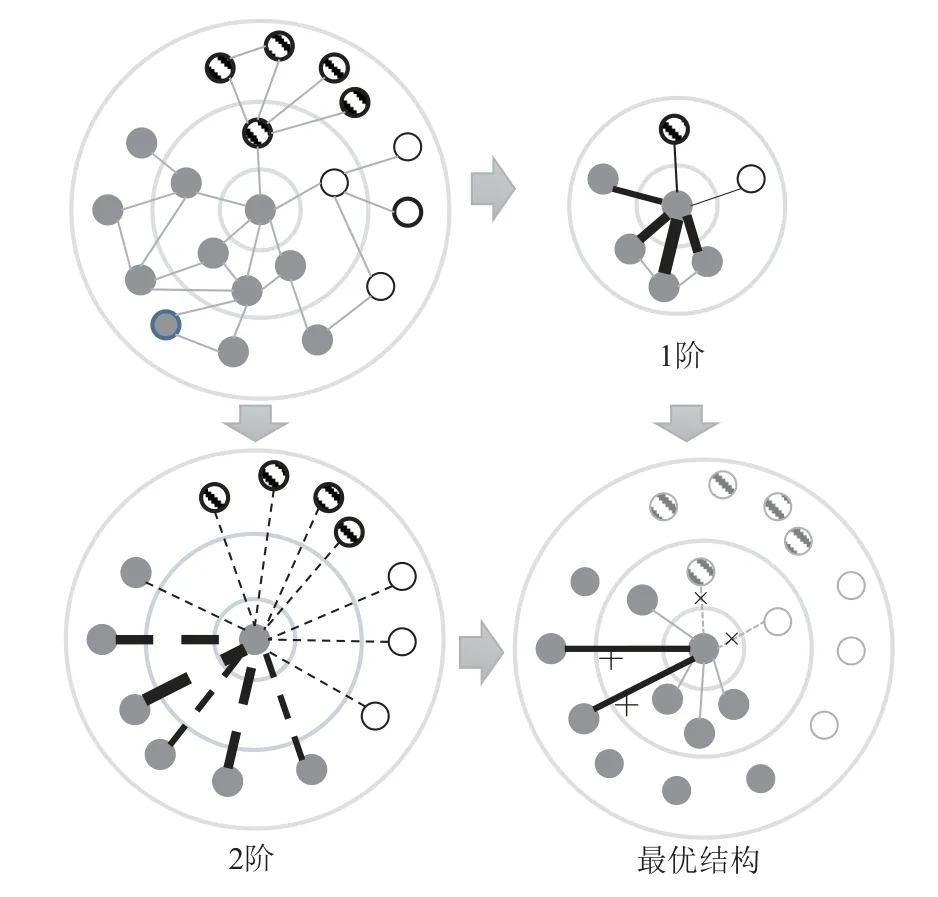
Fig.2 Optimal optimization effect of node local（secondorder）subgraph图2 节点局部（2 阶）子图最佳优化效果

由于网络数据具有天然的树形结构[43]，所以理论上在任意节点为中心的子图中，可以很容易地在高阶邻居中找到更多与中心节点同标签的节点.通过计算每个节点之间的邻接相似值来近似2 个节点之间属于同类节点的概率，并且为了降低计算量，本文只对节点的局部子图内邻居（1 阶、2 阶邻居）进行计算.首先计算中心节点vi与 其2 阶子图（本文特指2-ego network）中所有邻居节点间的邻接相似值；然后对相似值进行排序，为每个中心节点选取最大Top-K邻接相似值对应的邻近节点，并重新建立边连接，其中K对应每个节点的度数.根据3.3 节和3.4 节的假设及理论证明，重构的边连接更倾向于使用2 阶邻居中的同类节点替换1 阶邻居中的噪声节点.通过对每一个节点的局部邻接优化，达到网络全局降噪的效果.

在实际的优化过程中我们发现，在节点vi的 度数Dii比较小的情况下，节点对邻接结构过于敏感，采用局部邻接相似相较于多阶邻接相似优化效果更好.如果节点度数较大时，局部噪声边的绝对值也会增加，通过随机游走可以获得更多高阶同类邻接信息，进行局部邻近相似计算时可以很轻松地挑选出同类节点.因此最终的局部优化策略是：根据全局节点的平均度数，设定一个阈值 β，如果节点度数小于β，则根据局部邻接矩阵进行优化，如果节点度大于β值，就使用多阶邻接矩阵进行边优化，详细过程如算法1.

算法1.拓扑优化算法.

3.3 优化框架流程图与复杂度分析

我们对整个优化框架的逻辑进行了梳理，如图3所示.具体来说，首先基于局部同质性进行了局部邻接分布特性的推理证明；然后通过分析1 阶邻接与节点分类之间的关系得出本文的研究动机，并使用截断随机游走的方式获取到高阶邻接的近似转移矩阵S；最后通过计算任意节点与其2 阶内邻接节点之间的高阶转移相似性对该节点的1 阶邻接进行重构优化.

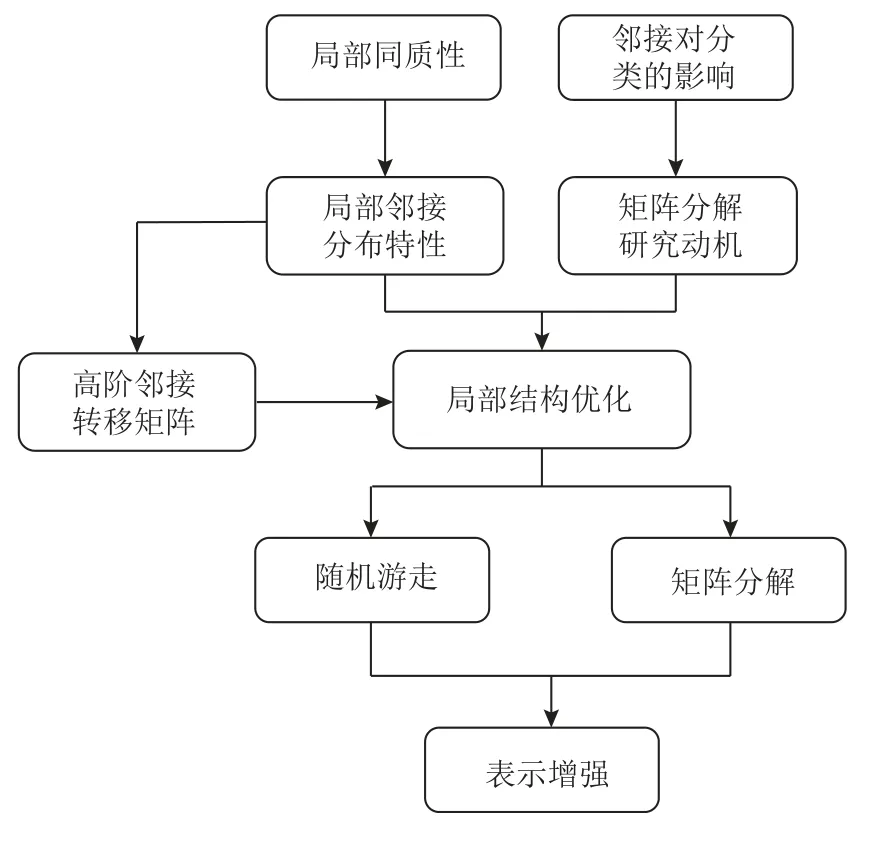
Fig.3 Flow chart of optimization framework图3 优化框架流程图

为了得到S，必须对于每个节点的高阶邻接进行采样获取矩阵M，这一步的时间复杂度为O(|V|×w×l).然后计算每个节点对之间的高阶转移相似距离，由于矩阵M是稀疏的，这一步的时间复杂度为O(|V|2).为每个节点选取最大Top-K邻接时，只需获取到最大K个节点即可，其时间复杂度为O(d×logw×l)，d是网络所有节点的平均度数.因此，优化过程的总时间复杂度为O(|V|×w×l+|V|2+d×logw×l).

4 实 验

4.1 实验设置

4.1.1 数据集

本文使用6 个公开数据集，包括3 个航空交通网络、2 个社会网络和1 个引用网络.Brazil，Europe，USA 是航空交通网络数据集，数据集中的每个节点对应一个机场，边表示机场之间存在商业航班[44].它们的分类标签是根据航班或通过机场的人测量的活动水平来分配的.Wiki[45]是社交网络数据集；Blogcatalog[46]是一个由博客作者提供的社会关系网络数据集，标签表示作者提供的主题类别，所有节点被划分为6 个类.Citeseer[29]是一个研究论文引文网络数据集，节点为出版物，边缘为引文链接，所有节点被划分为6 个区域.每个数据集具体的节点数、边数、类别和平均度数统计见表3.

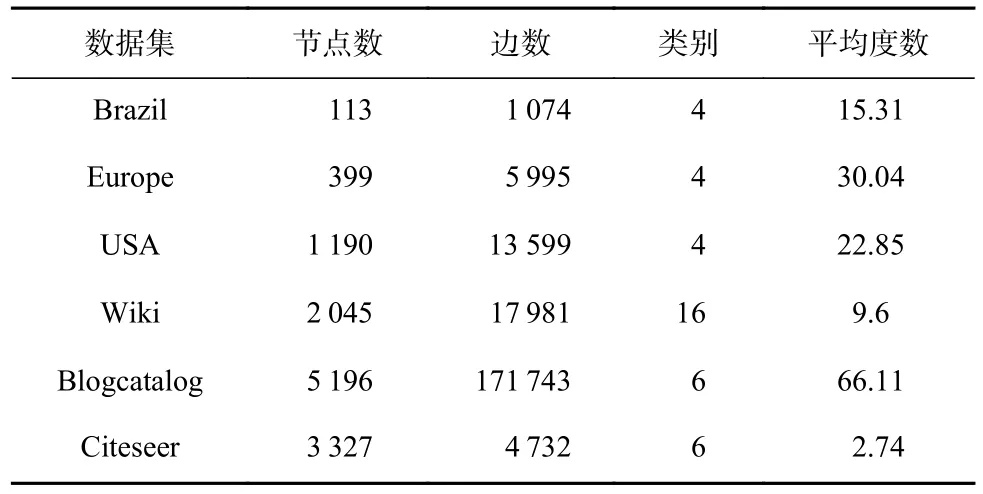
Table 3 The Statistics of the Datasets表3 各数据集的统计情况

4.1.2 基线方法

为了验证优化策略的性能，将采用以下9 个基线算法进行实验：

1）谱聚类（spectral clustering，SC）[21].它是一种矩阵分解算法，我们取图G的标准化拉普拉斯矩阵顶部的d个特征向量作为节点的特征向量表示.

2）isomap[47].它是一种半监督图卷积网络模型，它通过从邻居中聚合信息来学习.

3）图因 式分解（graph factorization，GF）[48].它 的信息网络可以用一个亲和矩阵来表示，通过矩阵分解，可以用一个低维向量来表示每个顶点.图因式分解通过随机梯度下降优化，能够处理大型网络.它只适用于无向网络.

4）局部线性嵌入（locally linear embedding，LLE）[19].它是一种半监督图卷积网络模型，通过从邻居中聚合信息来学习.

5）DeepWalk[25].它是一种用于社交网络嵌入的算法，只适用于具有二值边缘的网络.对于每个顶点，从顶点开始截断随机漫步用于获取上下文信息.

6）LINE[31].它定义了损失函数来分别保持1 阶或2 阶的接近性.在优化损失函数之后，将这些表示连接起来.

7）Node2vec[26].它的思想同DeepWalk 一样，生成随机游走序列，对序列采样得到的节点与其上下文组合，然后用处理词向量的方法对这样的组合建模得到网络节点的表示.不过在生成随机游走过程中做了一些创新.

8）SDNE[5].它使用一个自动编码器结构来同时优化1 阶和2 阶相似度（LINE 是分别优化的），学习得到的向量表示能够保留局部和全局结构，并且对稀疏网络具有鲁棒性.

9）Infwalk[49].它简化了有限窗口长度T网络PMI矩阵的已知表达式，并利用图的伪逆推导出T→∞的矩阵表达式.该表达式加强了基于Skip-gram 的网络嵌入方法和类光谱嵌入方法之间的联系.

本文所有的实验都是在一台拥有4 个3.60 GHz Intel 内核和20 GB RAM 的Windows 机器上进行的.

4.1.3 评价指标

对于标签分类任务，采用了Micro-F1 和Macro-F1 来评估算法性能.具体的，对于一个标签a，分别用TP(a)，FP(a)，FN(a)表示预测为a的实例中的真阳性、假阳性和假阴性的数目.假设C是整个标签集.定义为：

其中F1（a）是标签a的F1-measure，Macro-F1 是 给每个类同等权重的度量，Micro-F1 是给每个实例同等权重的度量.

对于链接预测，本文使用平均精度（average precision，AP）和平均精度均值（mean average precision，MAP）来评估性能，计算方法为：

其中，precision@k表示返回实例相同的权重，V是节点集，index(j)为第j个顶点的排序索引，Ti(j)=1表 示节点vi与 节点vj有链接，Q为查询集.

本文采用F-B 算法[50]对网络进行社区划分，用模块度（modularity）[51]衡量社区划分的效果，可以理解为社区内边的权重减去所有与社区节点相连的边的权重和，对无向图理解为，社区内边的度数减去社区内节点的总度数.具体定义为：

4.1.4 参数设置

在3 种矩阵分解算法中，搜索样本的近邻个数n_neighbors=5，降维后的维度n_components=30.DeepWalk，LINE，Node2vec，SDNE 算法表征维度设置为128，针对6 个数据集的分类任务训练都使用了20%的数据，其他的参数设置是基于默认值或提出该方法的论文中指定的值.对于本文提出优化过程涉及到的3 个超参 β,w,l，我们采用网格搜索来选择每个数据集的最佳超参，在局部边优化中的阈值β=5，w∈{3,4,5}，l∈{5,6,…,9}.为了确保实验结果能够反映方法真实的性能，所有实验都进行了10 次训练预测，然后求得均值.

4.2 节点分类

本文分别在上述的6 种数据集进行了分类实验，同时对比了网络优化前后在9 种算法的分类结果，以上9 种算法包括了矩阵分解、随机游走、深度学习三大类技术路线的图嵌入方法，并且每一种都具有其技术路线的代表性.具体分类结果如表4 和表5所示.可以观察到，经过优化之后的网络数据在多个算法分类结果对应的Micro-F1，Macro-F1 值都得到了提升，尤其是在航空网络中的Brazil 数据集中，Deep-Walk，LINE，Node2vec，SDNE 这4 种算法的Micro-F1值提升效果分别达到了23.11%，6.89%，14.93%，8.73%.在其他数据虽然也得到了提升，但是效果相对于3个航空网络数据集的提升幅度相对较小.同样的，以上4 种算法在Wiki 数据集的分类增强的Micro-F1 提升分别只有0.01%，1.01%，0.27%，1.58%.相较于其他2 类网络数据，航空网络中每个节点的标签由机场的活动水平来分配，即此类网络的节点标签受其结构信息的影响更大，而社交网络和引文网络中的节点标签与其节点自身的特征关系密切.通过分类结果可以看出，LSOS 优化策略更加适用于节点标签与网络结构密切类型的数据集.总体而言，本文提出的优化策略在3 类6 个数据上的9 个算法得到了不同程度的增强效果，验明了本文所提LSOS 策略的有效性.

Table 4 Micro-F1 Value of Node Classification Before（After）Optimization for All Baselines表4 各基线算法优化前（后）节点分类的Micro-F1 值 %

通过改变不同的训练比例，观察分类结果，选取基线算法中的DeepWalk，LINE，Node2vec 这3 个典型的图表示学习算法，在Brazil 和Europe 这2 个数据集上进行了分类Micro-F1 数值变化展示，如图4 所示，En表示优化后的效果.对于Brazil 数据集，DeepWalk算法从开始随着训练比例增加对应的AP也相应提升，而到达60%之后AP反而降低了，这可能是参与训练的节点比例过大导致算法模型训练过拟合.3 种算法相较于优化前的结果在任意训练比例的AP都有提升，而且具有同样的增长规律，优化后的网络表示效果相对于原始数据始终保持着明显优势.

为了验证本文优化策略的稳定性，我们对比了与本文工作类似的优化算法NEU，该算法的本质是对其他图嵌入算法最后的节点表示进行高阶近似计算，达到表示增强的效果.而本文所提优化策略LSOS是通过结构优化达到表示增强.NEU 和LSOS 这2 种策略与具体的算法模型都没有直接的关系.具体在Europe，USA，Wiki，Citeseer 这4 个数据集的分类任务对比了这2 种策略对于分类结果Micro-F1 值的增强效果.如图5 所示，相较于NEU，本文所提LSOS 增强策略更加稳定，在4 个数据集中都具有积极效果，而NEU 虽然在Wiki 数据集上的整体效果好于LSOS，但在Europe 数据集反而带来了负面效果.在Citeseer数据集中表现尤为明显，从增强结果可以看到，NEU对于LINE 算法的增强显著，而在DeepWalk 算法中居然得到了负效应，与此同时，LSOS 策略虽然在LINE 算法上没有NEU 效果好，但对4 种算法都有积极影响，进一步验证了LSOS 策略的稳定性与较好的适用性.

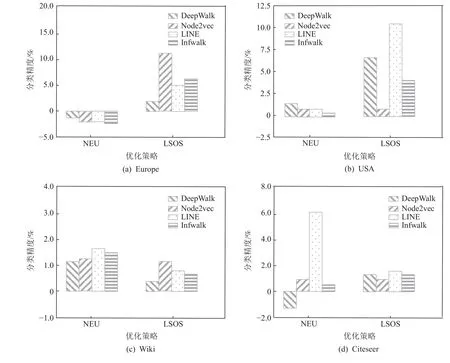
Fig.5 Comparison of NEU and LSOS enhancement effect（Micro-F1）图5 NEU 与LSOS 增强效果对比（Micro-F1）

4.3 连接预测

本文对优化前后的连接进行了测试，结果如表6所示.由表6 可以看到，经过优化之后的网络，在连接预测任务中对应的MAP和AP值，除了个别算法的数据集，总体表现都优于原始的数据集.我们可以观察到连接预测结果降低的3 种算法都属于矩阵分解类的图嵌入算法，而基于随机游走技术路线的2种算法几乎都得到了提升.这可能是优化处理之后网络社区成小簇团的形式导致矩阵分解类图嵌入提取到的表征较少，而基于随机游走类算法受此类原因影响较小.虽然进行了边优化，但是还是存在噪声边，在预测指标计算中，噪声边也算作正类预测目标，并没有限定为类内边，由此产生了预测误差.需要注意的是，连接预测任务是分别对优化前后的网络进行连接预测，主要是想通过预测结果证明优化后的网络结构能够增强同类节点的链接性.

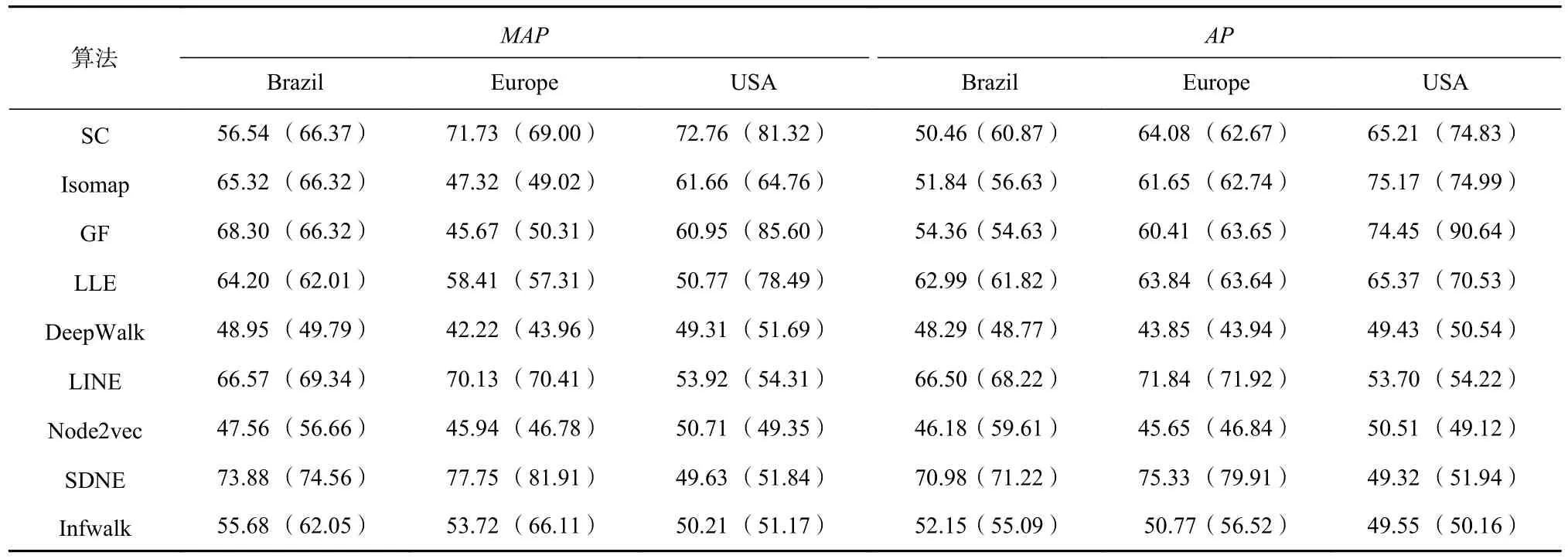
Table 6 Results of Link Prediction Before（After）Optimization for All Baselines表6 各基线算法优化前（后）链接预测的结果 %

4.4 可视化与社区发现

在可视化任务中，选取了Europe 和USA 数据集进行可视化，为了保持一致，全部使用DeepWalk 算法学习到的优化前后节点表示进行可视化展示.如图6 所示，Europe 和USA 这2 个数据集的节点表示优化前同类节点分布比较分散，优化之后的同类节点分布明显聚集.进一步对这2 个数据集优化前后的节点表示进行社区发现任务分析，具体结果如图7所示，分图题的括号中的2 项FB，modularity 分别为2 种社区划分指标.使用FB 算法对Europe 节点表示优化前后分布划分出3 个和8 个社区，而实际社区数为4 个，分析认为，优化之后的非同类节点之间连接边减少，同类节点形成紧密的局部社团.相较于优化前社区之间重叠导致边际模糊，优化后的结构更加容易区分.使用模块度对优化后社区划分进行评估，2 个数据集模块度都得到提升，验明了本文优化策略的有效性.

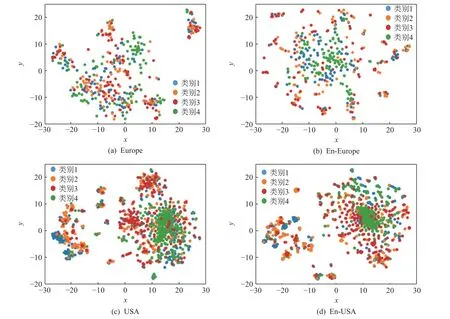
Fig.6 DeepWalk visualization before and after optimization图6 优化前后DeepWalk 的可视化

Fig.7 The results of network community division before and after optimization图7 优化前后网络社区划分的结果

4.5 有效性分析

本节分析多个基线方法都得到性能提升的原因.由于优化前后只对边进行了操作，我们将关注点集中在优化前后连接边的变化上.如图8 所示，在Brazil，Europe，USA，Wiki 这4 个数据集上，分别基于NO，JC和本文相似计算策略优化前后的网络边统计情况.其中Pe≥ 5，表示该网络中PE 值大于等于5 的节点数量占全部节点的比例；Interclass 表示该网络中，类内边数量占所有网络边总数的比例.通过图8 可以看到，对比其他优化算法，经过本文策略优化后的4个数据集中，Pe≥ 5的节点比例和类内边（Interclass）的比例都得到最佳提升.在Brazil 数据集的初始Pe≥ 5，节点比例等于40.75%，而通过NO，JC，LSOS 优化之后分别增至41.26%，38.23%，46.81%.初始Interclass 的比例等于69.78%，优化之后分别是71.43%，70.28%，74.72%.通过本文提出的相似计算方法相较于NO，JC这2 种传统算法在优化之后的效果更加显著，验证了节点对应的高阶转移之间的相似性可以很好地反映节点之间的相似性.同样的在其他3 类数据集中，LSOS 策略都取得了最佳效果.由于Pe≥ 5和Interclass这2 个指标都反映了数据集本身的一个社区分布情况，其对应的值越大说明网络社区越明显.本文认为优化策略提升了网络自身结构，使其能够更加适应不同的基线方法.

Fig.8 The results of using a variety of edge similarity indexes for optimization图8 利用各种边相似指标进行优化后的结果

为了清晰地展示优化前后的效果，我们使用karate 数据集进行了社区分布可视化，如图9 所示，该网络共有 34 个节点和78 条边，其中34 个节点表示某空手道俱乐部的34 名成员，34 个节点分为2 个社区.优化之前2 个社区之间连接较多，边界比较模糊导致社区划分效果较差，该网络对应的社区划分模块度等于0.35.具体的如节点30 号，初始的1 阶邻居包括{1，8，32，33}，其中{1，8}为非同类节点，通过结构优化重构之后，新的邻居节点换成了{15，28，32，33}，全部都是同类节点.优化后的模块度等于0.43，从图9 可以看出明显的社区边界.

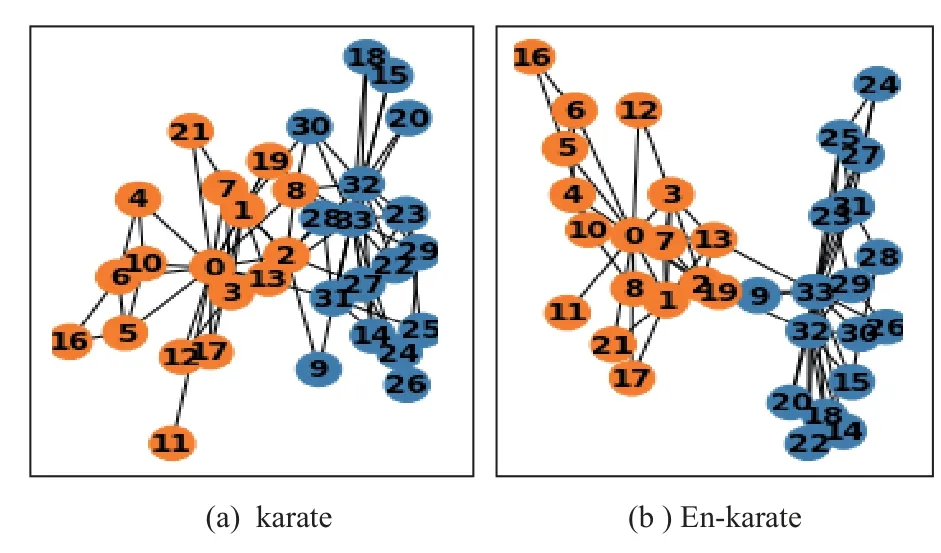
Fig.9 Community visualization effect before and after structural optimization of karate dataset图9 karate 数据集结构优化前后社区可视化效果

5 结论

本文首先提出2 种新的邻接相似矩阵构建方法，通过结合局部或者高阶邻接信息来近似计算2 个节点之间的结构相似性，基于此提出了一种2 阶子图内边优化策略.然后通过大量的实验验证了优化策略的有效性.在6 个公开数据集上对比了多个最先进的算法模型.实验结果显示，经过优化之后的多个数据在节点分类、连接预测和社区发现任务中性能都得到了增强.本文的优化策略可以被用在不同的网络分析任务中，与不同类型的数据集，既可以配合不同算法进行训练，又可以作为一种网络数据预处理.

作者贡献声明：唐正正提出了研究思路，完成实验并撰写论文初稿；汪洋和洪学海提出指导意见并修改论文；班艳审查论文；姚铁锤参与论文修改与结果分析；乔子越对模型框架和实验设计提出修改建议.