算法公平与公平计算

范卓娅 孟小峰

（中国人民大学信息学院 北京 100872）

（fanzhuoya@ruc.edu.cn）

公平是社会的基石，人类对公平的追求由来已久.早在公元前25 世纪，古埃及人就发明了天平，用于保证交易双方的公平.古埃及的《亡灵书》[1]更是以绘画的形式记录了亡者由公平女神玛特引领，在天平上进行心脏称量，并由冥王进行审判的情景.这充分体现了公平在人类血脉中留下的深刻烙印.在此时期，人类社会尚处于原始公社阶段，由于生产力极为低下，人们在劳动中平等互助，劳动产品在全体公社成员中实行平均分配，正如卢梭所言“原始社会人人平等”.

随着生产力的发展，人类社会逐渐出现了利益不同的阶层和阶级的分化，人类对公平的关注开始从劳动转向对剥削、压迫等不公平现象的批判.古希腊思想家柏拉图、亚里士多德等均针对公平问题阐述了不同的公平观.柏拉图在《理想国》中讨论了如何设计公平的国家，他认为公平的国家要求社会各阶层之间分工互助，以达到全体公民的普遍幸福.亚里士多德对公平进行了更为细致的划分，将公平分为分配公平与矫正公平.与此同时期，我国思想家孔子也在《论语》中提出“不患寡而患不均”的分配公平理念以及“有教无类”的教育公平理念.20 世纪60 年代后，西方社会已经发展进入资本主义阶段，贫富差距使得阶级对立进一步加剧，由此引发了人们对公平问题的激烈探讨，其中产生的代表性理论如亚当斯的公平理论、罗尔斯的“无知之幕”等.亚当斯在1965 年提出公平理论[2]，该理论聚焦于薪酬分配公平，认为公平是员工进行社会比较与历史比较而产生的主观感受.罗尔斯在《正义论》[3]中提出“无知之幕”的思想实验，他将人们从当下的社会角色和身份地位中剥离出来，回归到最原始的平等状态：每个人都不知道自己将在社会上扮演什么角色.罗尔斯认为在这种博弈境况下，人们会共同制定出公平的社会规则以保护社会中的弱势群体.这些理论为后世解决公平问题提供了方法论指导，但不可避免地带有历史局限性.

近代社会的演进由基础设施的发展决定，不同阶段的基础设施带来不同的生产要素和社会结构.如表1 所示，交通、电力、信息等基础设施的建设发展，为社会发展提供了新的生产工具与方式，促使社会从工业革命1.0 时代逐步步入工业革命4.0 时代.在社会变革中，数据、算法逐渐成为社会的基本要素，由此而生的算法公平问题也不尽相同.在此背景下，本文所讨论的算法公平不仅仅限定于作用于人的决策算法，而是将其概念拓展至广义的算法公平.广义的算法公平，是指在化解社会矛盾纠纷中寻求实现公平的算法[4]，至少可追溯至17 世纪.1654 年，数学家帕斯卡与费马就在信件往来中开创了概率论的研究，讨论了如何在中断的赌博中公平分配赌注的问题[5].在工业革命3.0 时代之前，算法公平问题主要集中在此类公平分配问题上，其根源是人与人之间由于利益纠葛而产生的不信任，即社会偏见.随着互联网与云计算基础设施的建设发展，社会进入工业革命3.0时代，算法公平问题主要来源于人们对海量高速的大数据的不信任，即数据偏见.随着万物互联基础设施的深入推进，在工业革命4.0 时代，人工智能技术悄然重塑了人们的生产生活方式，人工智能算法渗透至社交[6]、医疗[7]、司法[8]等领域，可谓无处不在、无孔不入.在此阶段，算法公平问题主要来源于人们对黑箱模型的不信任，即模型偏见.由此可见，算法公平问题由来已久，且随着社会发展的进程不断花样翻新.

Table 1 Evolution of Algorithmic Fairness表1 算法公平问题的演进

在数据基础设施驱动下，社会面临数字化转型，算法公平问题更是尤为重要.算法给人带来的剥削将更为隐蔽，而影响将更为深远.针对该问题，一方面，国家监管部门日趋重视：2021 年、2022 年《中华人民共和国个人信息保护法》[9]与《互联网信息服务算法推荐管理规定》[10]接连发布，要求算法服务提供者不得利用算法在交易价格等交易条件上实施不合理的差别待遇.另一方面，工业界迫切需要技术手段对算法公平加以保障.尽管公平问题的研究在社会科学各领域由来已久，但大部分仅停留在定性的表述上.算法公平，作为计算机科学与社会科学的交叉问题，不仅要继承社会科学各领域的基本理论，更要从定性分析转向定量计算.因此，本文将实现算法公平的方法称为“公平计算”.然而现有的研究处于2种极端：社会科学领域的研究对于如何为算法公平计算提供理论基础的关注度不高；计算机科学领域的研究忽视了对社会科学理论方法的借鉴继承.

基于此，本文主要针对计算机科学与社会科学领域的算法公平研究的交叉融合进行探讨，重点强调算法公平需要具备公平计算的方法和能力.本文首先介绍算法公平的定义及构成要素.然后，根据社会的发展历程及算法公平的构成要素，将不公平的根源分为社会偏见、数据偏见以及模型偏见3 方面，并从这3 个方面对现有的算法公平计算方法进行总结说明.最后，对算法公平指标和公平方法进行实验评估，并进一步指出算法公平计算面临的挑战.

算法公平领域在国内外已有众多综述文章[11-15]，其中：Mehrabi 等人[11]在数据、模型和用户交互的闭环上对偏见的来源进行了详尽的分类；陈晋音等人[12]从数据和模型2 个角度对深度学习中的公平性研究进行综述；刘文炎等人[13]从公平表征、公平建模和公平决策3 个角度对可信机器学习的公平性研究进行总结；古天龙等人[14]以机器学习生命周期的角度从预处理、中间处理和后处理3 类方法对公平机器学习研究进行介绍；Pessach 等人[15]在介绍预处理、中间处理和后处理这3 类方法的同时，还特别分析了它们的适用场景.

但文献[11-15]均存在2 方面不足：一是关于算法的讨论局限于机器学习算法；二是关于公平方法的分类仅包括数据和模型2 个维度，而忽略了社会维度.因此，本文的创新之处主要包括3 点：

1）将公平问题所涉算法从机器学习算法推广至通用算法.公平问题不仅是机器学习算法具有的问题，更是通用算法可能具有的问题.进一步地，本文将算法公平的研究范围从狭义拓展至广义，从而涵盖了使用算法手段解决社会矛盾纠纷的问题.

2）将社会偏见下的算法公平纳入算法公平问题的分类.首先，社会偏见、数据偏见与模型偏见之间既存在历史发展关系，又存在相互作用关系，这使得本文提出的算法分类体系更加完整.其次，社会偏见下的算法公平计算方法对于数据偏见与模型偏见问题有重要的借鉴意义.比如目前数据偏见与模型偏见下的算法公平大多致力于实现不同群体在某种指标上的相等，而社会偏见下的算法公平说明了公平不等于平等.

3）实验对比了社会偏见下的算法公平与数据偏见、模型偏见下的算法公平的区别.本文在第5 节对不同的公平指标进行了实验计算，并比较了不同公平指标间的关系.

1 算法公平的内涵

在研究算法公平问题之前，我们首先需要了解什么是算法公平.因此，本节将从算法公平的定义出发，说明算法公平的构成要素；然后根据算法公平的构成要素，将算法公平分为社会偏见下的算法公平、数据偏见下的算法公平以及模型偏见下的算法公平3 类.

1.1 算法公平的定义

算法公平是指算法不会根据个体或群体的先天特征或后天特征，对其产生歧视或偏见[11].因此，算法公平的定义可分为个体公平（individual fairness）与群体公平（group fairness）这2 类[16].个体公平是指任何2 个相似的个体都应该受到算法相似的对待，通常需要一个与任务相关的距离度量来刻画每对个体间的相似度.群体公平的基本理念是算法的输出不应该受与任务无关的属性影响，如性别、宗教、种族等属性不应该影响算法的输出，这些属性又被称作受保护属性（protected attributes）或敏感属性.受保护属性的定义通常参照法律法规，表2 展示了不同国家地区的法律规定的受保护属性.在群体公平下，按照受保护属性划分群体，不同的群体应受到算法相似的对待.

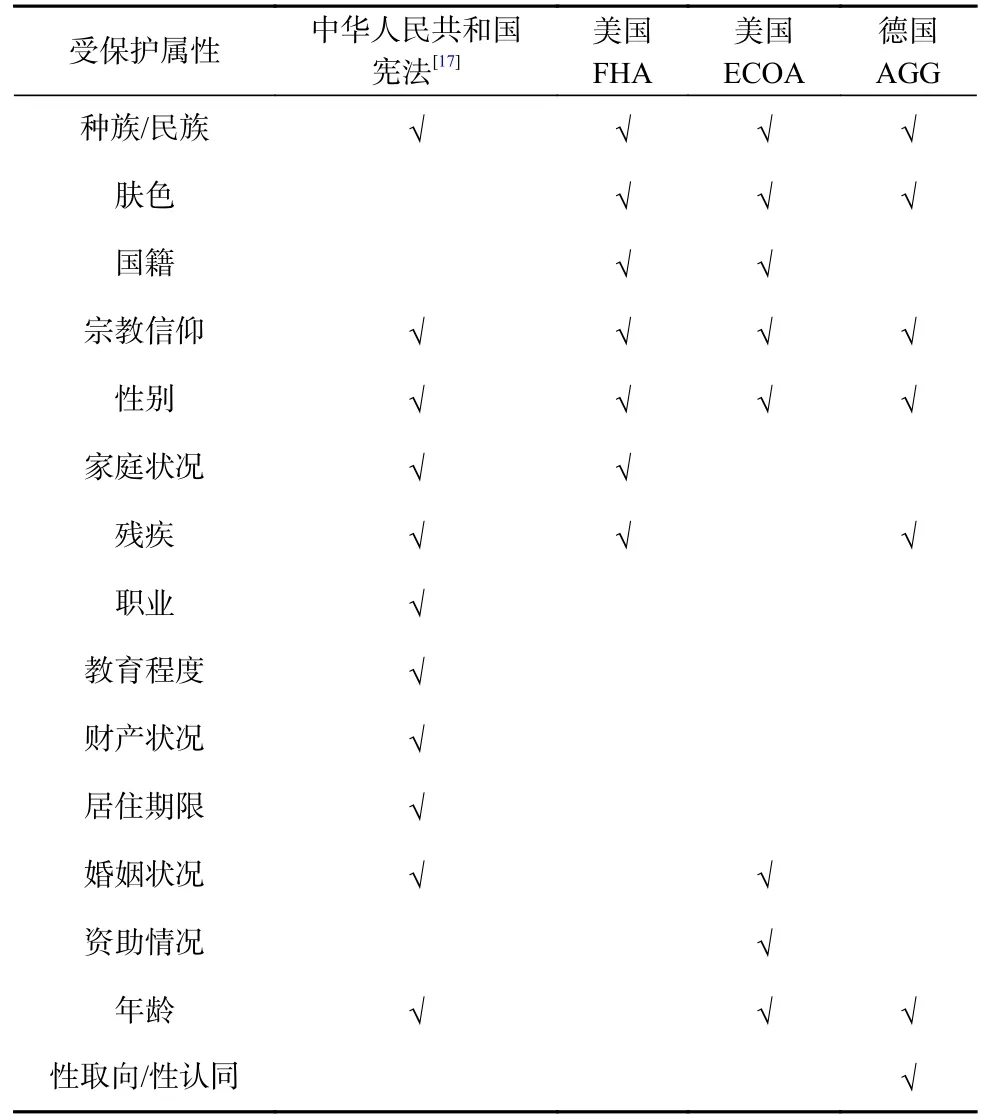
Table 2 Protected Attributes Under the Laws of Different Countries表2 不同国家法律规定的受保护属性

参考Lippert-Rasmussen[21]对歧视的形式化定义，本节给出算法公平的形式化定义：

定义1.算法公平（algorithmic fairness）.算法 M 对于个体O1（相对于个体O2）在输出out上是满足个体公平的，当且仅当不存在2 种情况：

1）存在与任务相关的距离度量dist，使得dist(O1)≈dist(O2)；

2）M通过输出out对待O1与O2不同.

算法 M 对于群体G1（相对于群体G2）在输出out上是满足群体公平的，当且仅当不存在2 种情况：

1）存在受保护属性A，使得G1具有属性A（或M认为G1具有属性A），G2不具有属性A（或 M 认为G2不具有属性A）；

2）相对于G2，M 通过输出out对待G1更差，且正是因为 M 认为G1具有属性A而G2不具有属性A.

基于算法公平的定义，可以发现：算法公平的主体是算法；算法公平的客体是个体或群体；算法公平的行为是算法的输出.

1.2 算法公平的分类

根据算法公平参与者的不同，算法公平的构成要素可分为数据提供者、服务提供者、公平监管者以及用户4 类，如图1 所示.

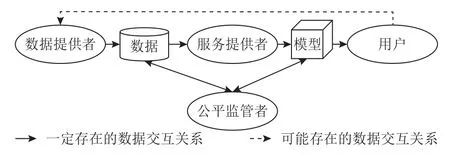
Fig.1 Components of algorithmic fairness图1 算法公平的构成要素

1）数据提供者.数据提供者是指对数据进行收集、加工及标注等的第三方.

2）服务提供者.服务提供者使用数据提供者提供的数据训练模型，并为算法使用者提供算法服务.

3）公平监管者.公平监管者是指确定公平标准并对算法进行监管审计的政府、法院等机构.

4）用户.用户是算法公平的客体.当用户与算法的交互数据再次被数据提供者收集时，则可能会造成偏见的恶性循环.

算法公平问题源自这四者与数据、模型之间的交互.若仅考虑算法的输入输出，则算法公平可以分为数据与模型2 个维度.但由于算法公平问题是一个社会问题，还应考虑4 类参与者之间的利益权衡，包括用户之间的利益分配、服务提供者提供的模型质量与公平监管者提出的公平约束之间的权衡等.因此，本文将算法公平分为社会、数据以及模型3 个维度.同时，这3 个维度间具有如引言所述的社会发展关系.基于算法公平的分类，下文将分别对社会偏见下的算法公平、数据偏见下的算法公平以及模型偏见下的算法公平进行介绍.这三者的内涵与评估指标之间存在交叉，其内涵区别在于：社会偏见下的算法公平依据公平的特殊性质进行划分，涉及多类参与者或体现公平的相对性；数据偏见与模型偏见下的算法公平依据现有研究通用的机器学习生命周期进行划分，数据偏见下的算法公平对应于预处理方法；模型偏见下的算法公平对应于中间处理与后处理方法.

2 社会偏见下的算法公平

在互联网诞生之前及互联网发展初期，公平问题主要来源于人与人之间的偏见与不信任，即社会偏见.社会偏见在社会分配中表现得尤为明显，由于人与人之间存在利益冲突，人们不信任分配方式，担心自己的利益受损.如果将分配方式视为一种算法，社会偏见问题即化归为算法公平问题，其目标是使参与人在博弈下达到一种平衡状态.根据损益情境，社会偏见下的算法公平可分为公平利益分配与公平损失分摊2 类.二者的区别在于：在利益分配中，每人希望分得的利益尽量多；在损失分摊中，每人希望分得的损失尽量少.

2.1 公平利益分配

公平利益分配发生于利益共享情境，如薪酬分配、教育资源分配、医疗资源分配等.蛋糕分割（cake cutting）[22-23]问题是公平利益分配的经典问题，常用于建模异质可分的有限资源分配.异质是指蛋糕由不同的成分组成，参与者不只关心蛋糕的大小，可能有人喜欢奶油，有人喜欢果酱；可分是指蛋糕可以分割成任意小的块，并且分割粒度不会影响蛋糕的价值.怎么才算蛋糕分得“公平”？研究者提出了2 种定义.

定义2.均衡（proportionality）.给定蛋糕区间 [0,1]，参与者集合 N={1,2,…,n}，每个参与者p对蛋糕有1个未知的估值函数Vp，分割程序分给每个参与者p的蛋糕为Cp，则均衡分割满足条件：

定义3.无怨（envy-freeness）.给定蛋糕区间[0,1]，参与者集合 N={1,2,…,n}，每个参与者p对蛋糕有1个未知的估值函数Vp，分割程序分给每个参与者p的蛋糕为Cp，则无怨分割满足条件：

即每个参与者都认为自己得到的蛋糕比别人的大，从而不会嫉妒他人.可见，无怨比均衡的要求更严格.

当n=2时，“一人切，一人选”是很自然的均衡分割方法，同时可以证明这种方法也是满足无怨的.假设A和B分蛋糕，“一人切，一人选”的算法流程为：

①A将蛋糕切分成2 块；

②B选择其中的1 块；

③A最终分得剩下的1 块.

如果A切分的2 块蛋糕一大一小，那么B会选择更大的那块，因此为了避免自己吃亏，A就会将蛋糕分成自己认为价值相等的2 块.最终结果为VA(CA)=VA(CB)，VB(CB)≥VB(CA)，即满足无怨.

当n>2时，可以基于“一人切，一人选”的方法递归地实现均衡分割.前n-1个人递归调用分割程序；然后，第n个人让前n-1个人都把自己手里的蛋糕分成n份，并从每个人手中选出n份中的1 份.同理可证明这种方法是均衡的，但不满足无怨.以n=3为例，A和B先采用“一人切，一人选”的方式将蛋糕分成2 块，然后将各自的蛋糕都分成3 份，C从A的手中选出1 份，从B的手中选出1 份.如果A和B合谋将整个蛋糕分给了A，那么C会得到蛋糕的，A得到蛋糕的，不满足无怨.

尽管蛋糕分割问题历史悠久，但依然吸引着众多研究者前赴后继.这是因为构造多人的无怨分割比较困难：Brams 等人[24]证明了当n取任意值时，都存在无怨分割方法，但该分割方法的运行时间即便在n=4时也是无界的.针对运行时间的无界问题，20 年后，Aziz 等人[25]提出了一种时间复杂度为的无怨分割方法.可见实现多人的无怨分割复杂度极大.目前只有3 人的无怨分割有相对完美的解法[22]，假设A，B，C分蛋糕，其算法流程为：

①A将蛋糕切分为认为相等的3 份X1,X2,X3,即

②B从3 份中选出自己认为最大的那块进行修剪.例如，当VB(X1)>VB(X2)≥VB(X3) 时，B从X1中剪去X′，使得VB(X1X′)=VB(X2).

③按照C，B，A的顺序依次从修剪剩下的3 块中选择1 块.算法流程中，即从X1X′，X2，X3中进行选择.对于被修剪过的那块，即X1X′，如果C没有选择该块，B就得选择该块.在B和C中，设最终选择被修剪过的那块蛋糕的人为T，没选择该块的人为.

④将剪掉的那块，即X′，分成认为相等的3 份.

⑤按照T，A，的顺序依次选择1 份.

2.2 公平损失分摊

公平损失分摊发生于损失共担的情境，如房租分摊、保费分摊、环保成本分摊等.差别定价问题是公平损失分摊的经典问题，是指企业针对顾客、产品、时间、地点等因素的差异，为生产的产品设定不同的销售价格.顾客细分定价是差别定价的一种典型形式，即企业将同一种商品或服务以不同的价格卖给不同的消费者.

针对该问题，在商品定价的场景下，Cohen 等人[26]研究了施加公平约束对社会总福利的影响.他们认为商家的目标是为每个消费者群体分别定价以最大化利润，在此基础上提出了4 种公平约束定义：价格公平、需求公平、消费者剩余公平和未购买估值公平.假设商家将1 种商品卖给2 个消费者群体，记为群体0 和群体1.商品的单位成本是c.对于群体i=0,1，群体i的人数是di，商家的定价是 ρi.群体i中的消费者对商品的估值为 τi∼Ti(·)，则群体i购买商品的比例为(ρi).消费者剩余定义为消费者对产品的估值与实际购买价格的差值，群体的消费者剩余Si(ρi)=E[(τi-ρi)+].商家从群体i中获利为Ri(ρi)=di(ρi-c)×(ρi)，在没有公平约束的情况下，商家的目标是获利最大，即目标函数为=arg maxRi(ρi).

4 种公平约束定义为：

1）价格公平是指商家给每个消费者群体的定价相似，即 ρi相似；

2）需求公平是指每个消费者群体的购买比例相似，即(ρi)相似；

3）消费者剩余公平是指每个消费者群体的平均剩余相似，即Si(ρi)相似；

4）未购买估值公平是指每个消费者群体中未购买的消费者对该产品的平均估值相似，即E[τi|τi<ρi]相似.

Cohen 等人[26]使用参数 α调节公平约束的严格程度，实验发现，一定程度的价格公平下，社会总福利随着约束程度的增强而提高；当价格公平约束过于严格时，社会总福利反而会降低.在未购买估值公平下，社会总福利随着约束程度的增强而提高，但其中某个消费者群体的需求可能会消失.

在保险定价的场景下，Donahue 等人[27]研究了基于期望的定价、基于破产的定价2 种定价方式，以及均等定价、比例定价2 种公平目标.假设投保人分为高风险和低风险2 类群体，N为投保人集合.高风险群体共有nH人，风险概率为rH.低风险群体共有nL人，风险概率为rL.被保物品的价值为ν，收取的总保费为C.则在基于期望的定价下，有

其中，ri表示第i个人的风险概率.

在基于破产的定价下，设保险公司1 年内赔付总额为随机变量 χ，给定破产概率为常数q，收取的保费为 Cq，则有

均等定价是指不同风险群体的保费相同；比例定价是指不同风险群体的保费与其风险概率成正比.Donahue 等人[27]证明了在基于破产的定价下，由于定价函数具有外部性，均等定价和比例定价均有利于高风险群体.此外，高风险群体相对风险越高，低风险群体需缴纳的保费越少，说明此种定价方式具有一定的“反社会性”.

在商品定价中，严格的价格约束反而使得社会总福利降低；在保险定价中，基于破产的定价使得人们期望别人的风险比自己高.这体现了算法公平的社会性，说明在某些场景下不够合理的公平定义可能会带来期望之外的负面影响.

蛋糕分割问题与差别定价问题分别是个体公平与群体公平的典型范例，二者对比如表3.蛋糕分割问题考虑利益所得者之间的博弈，体现了公平的相对性，但无法摆脱个体公平计算复杂度高的缺点；差别定价问题考虑监管者与服务提供者之间的博弈，体现了公平的社会性，但忽略了群体内的差异性.

Table 3 Comparison Between Cake Cutting Problem and Price Discrimination Problem表3 蛋糕分割问题与差别定价问题对比

3 数据偏见下的算法公平

随着计算机技术的高速发展，云计算技术逐渐崛起，我们步入了大数据时代.源源不断产生的数据促使机器学习算法逐渐兴起，大数据时代的数据偏见问题开始进入研究视野.由于机器学习算法极其依赖于训练数据，训练数据中存在的偏见极有可能使算法输出产生偏见，即“偏见进，偏见出”（bias in,bias out）.因此，数据偏见下的算法公平致力于在源头上解决算法公平问题，在训练数据输入算法之前消除其中存在的偏见，即预处理（pre-processing）.如：IBM 于2019 年发布多样性人脸（diversity in faces，DiF）数据集[28]，提供分布均衡多样的人脸图像，以期减少人脸识别系统的偏见问题；Yang 等人[29]针对ImageNet 的数据收集流程进行分析，在“person”子类中使用过滤与平衡数据分布的方法，试图缓解数据集中的公平问题.表4 梳理了近年来数据偏见事件的原因与危害，可以发现：数据偏见事件在各领域相似且频繁地出现，对人们的人格权与平等就业权造成潜在危害.

Table 4 Causes and Harms of Data Bias Events in Recent Years表4 近年来数据偏见事件的原因与危害

根据数据偏见的具体来源，数据偏见可以分为涌现偏见、历史偏见、数据类别不平衡等类型.

1）涌现偏见.涌现偏见[11,36]是指系统在与用户交互的过程中，系统受到人类社会文化、价值观等因素的影响，从而表现出的偏见.例如聊天机器人在刚上线时表现正常，经过一段时间的使用后，在与用户的交互中学习到人类社会中的偏见.

2）历史偏见.历史偏见[11]是指历史数据中已经存在人类社会中的偏见未经过处理即作为模型输入.例如谷歌新闻中有关医生的描述大多数与男性相关，有关护士的描述大多数与女性相关，由此未经处理而训练出的词向量同样会表现出性别刻板印象.

3）数据类别不平衡.数据类别不平衡是指数据集中的某一类样本数远少于其他类，从而导致模型在少数类上表现较差.例如谷歌照片识别模型与Facebook 视频主题推荐模型的训练数据中黑人样本较少，导致模型在黑人测试集上的效果较差.

此外，根据训练数据中是否包含受保护属性，数据偏见可分为显式偏见与隐式偏见2 类.显式偏见是指训练数据中直接含有受保护属性而导致的偏见，如受保护属性群体的样本数量不平衡，某些群体样本数量过少使得模型在该群体样本上表现较差.如图2 所示，A为受保护属性，为训练数据中受保护属性之外的其他属性，Y为算法输出结果，显式偏见表明Y与A之间存在直接相关性.此类偏见可用不平衡数据处理技术去除.隐式偏见是指训练数据去除了受保护属性，但仍存在其他与受保护属性相关的特征信息而导致的偏见，如词向量中隐含的偏见、邮政编码中隐含的种族信息等.如图2 所示，训练数据中的受保护属性A已消除，但由于训练数据中仍存在隐变量H与A具 有相关性，算法输出结果Y与H具有相关性，间接导致Y与A具有相关性.此类偏见需使用公平表示学习技术去除.

Fig.2 Explicit bias and implicit bias图2 显式偏见与隐式偏见

3.1 不平衡数据处理

常用的不平衡数据处理的方法有数据重赋权、数据重采样、数据增强等.数据重赋权是指调整样本在目标函数中的权重.如Amini 等人[37]利用变分自编码器学习数据集的潜在结构，然后根据学习到的潜在分布调整训练过程中数据点的权重.Kamiran 等人[38]认为无偏的数据集应满足样本标签与受保护属性相互独立的条件，假设数据集 D 中样本为X，标签为Y，受保护属性为A，则数据集的期望分布为

数据集的实际分布为

因此，Kamiran 等人[38]将重赋权函数定义为

当W(X)>1，即样本点比例比期望比例少时，增加样本点的权重；当W(X)<1，即样本点比例比期望比例多时，减少样本点的权重.

数据重采样可分为欠采样和过采样2 类.欠采样旨在减少多数类的样本量，如随机欠采样对多数类的样本进行随机删除.过采样旨在增加少数类的样本量，如随机过采样对少数类的样本进行随机复制.随机欠采样方法与随机过采样方法均存在缺陷：前者会丢失某些重要样本的隐含信息；后者容易使模型产生过拟合.基于随机过采样，Chawla 等人[39]提出了改进方案——合成少数类过采样算法（synthetic minority over-sampling technique,SMOTE）.SMOTE 的基本思想是合成与少数类样本相似的新样本：首先采用k近邻算法计算出每个少数类样本的k个近邻，然后从k个近邻中随机选择N个样本进行随机线性插值构造出新样本.针对无法进行数据重赋权的数据点，Kamiran 等人[38]设计了随机普遍采样与优先采样2 种采样方法.随机普遍采样首先将数据集根据二元受保护属性与二元样本标签交叉划分为4 组，然后在每组数据点中随机采样期望数目的样本.优先采样依赖于用训练数据提前训练好的朴素贝叶斯分类器，优先对靠近分类器决策边界的样本进行采样.

数据增强是计算机视觉领域的常用数据预处理方法，通过对图像进行几何变换（如翻转、旋转、平移、裁剪、缩放等）与颜色变换（如色彩调整、灰度、加噪、滤波等）2 类操作，可以有效提高图像数据的样本量和多样性.类似地，自然语言处理领域也发展出文本增强技术，通过回译、随机词与非核心词替换等方式扩增文本.如Zhao 等人[40]通过交换命名实体性别的方式减少指代消解任务中的性别偏见.

3.2 公平表示学习

由于不平衡数据处理无法解决隐式偏见问题，部分研究者致力于消除数据中存在的敏感属性信息，意图在输入数据X到输出结果Y的映射之间增加一个X的表示Z，使得Z中在不包含敏感属性信息的同时能很好地适应于下游的任务，即公平表示学习.McNamara等人[41]将公平表示学习的构成要素分为数据监管者（data regulator）、数据生产者（data producer）和数据使用者（data user）3 类.其中，数据监管者负责确定公平定义标准、确定原始数据并审计结果；数据生产者负责基于原始数据计算公平的数据表示，进行数据去偏；数据使用者负责基于去偏的数据训练模型.Zemel等人[42]提出了LFR（learning fair representations）方法，要求X到Z的映射满足统计平等.随后，众多研究者采用对抗性训练的方法进行公平表示学习.关于对抗性训练的分类存在争议，由于对抗性训练也是对目标函数的一种修改，部分研究者将对抗性训练划为模型去偏方法[12].但本文认为对抗性训练作为一种表示学习方法，其学习出的公平表示可迁移于不同的下游任务.从原始数据到表示的转换归属于预处理方法更为合适，因此本文将对抗性训练方法划分为数据偏见下的算法公平.如Madras 等人[43]提出了LAFTR（learning adversarially fair and transferable representations）方法，采用对抗性训练和迁移学习的方法训练可迁移于不同任务的公平表示，该方法支持基准率公平、准确率公平等公平定义.LAFTR 的目标函数如式（8）（9）所示：

其中X为输入，Y为标签，A为受保护属性，模型结构包含编码器f、分类器g、对抗器h和解码器k这4 部分，损失函数由分类损失LC、重构损失LDec和对抗损失LAdv这 3 部分构成.设Z=f(X,A)，首先，编码器f将X编码为潜在表示Z，分类器g根据Z来预测输出结果Y，分类损失LC用于控制Z能够分类准确；然后，解码器k将Z与受保护属性A解码回X，重构损失LDec用于控制Z包含X中的显著信息；最后，对抗器h根据Z来预测A，对抗损失LAdv用于控制Z中不包含A中的信息.

Alvi 等人[44]受领域自适应的启发，同样基于对抗性训练学习去偏的特征表示.该方法分为主要任务与辅助任务2 个分支：主要任务用于完成目标属性的分类；辅助任务包括受保护属性分类与混淆2个对抗目标，用于评估并移除特征表示中遗留的受保护属性信息.此外，基于对抗性训练的公平表示学习也可用于更多具有复杂数据类型与任务的应用场景.如：Bose 等人[45]使用生成对抗性训练的方式学习公平的图嵌入向量；Zhang 等人[46]将对抗性训练的公平表示学习方式应用于深度异常检测任务；Sweeney等人[47]在情感分析任务中，采用对抗性训练将受保护属性与情绪状态解相关；Ball-Burack 等人[48]针对推特有害信息检测的场景，将优先采样方法与对抗性训练加以结合，缓解该场景下的种族偏见.

但是对抗性训练成本高且难以优化，针对该问题，Shen 等人[49]采用对比学习的方法学习公平的表示，其损失函数为

其中 ：Lce为 交叉熵损失；Lscl为监督对比损失，用于在表示空间中将类别相同的相似样本拉近；Lfcl为公平对比损失，用于在表示空间中将受保护属性相同的相似样本推远.Hong 等人[50]将数据有偏场景分为偏差标签已知和偏差标签未知2 种情况：在偏差标签已知情况下提出了与Shen 等人[49]相似的目标；在偏差标签未知的情况下将偏差捕获模型与对比学习相结合.

4 模型偏见下的算法公平

随着人工智能时代的日益发展，算法黑箱使得人们开始质疑仅消除训练数据中的偏见是否足够.Baeza-Yates[51]指出机器学习模型在训练过程中也可能产生偏见，即模型偏见.造成模型偏见的原因有不合理的目标函数[52]、不合理的特征设计[53]等.针对此类偏见，部分学者致力于在机器学习模型训练或预测过程中实现某种公平度量指标上的均等，主要手段包括在模型训练的目标函数中引入公平约束、调整输出阈值等.如Li 等人[54]在联邦学习场景下将公平定义为不同设备间模型精度分布的方差，在模型训练过程中优化施加了公平约束的目标函数.根据机器学习算法的类别，模型偏见下的算法公平大致可分为公平有监督学习与公平无监督学习2 类.

4.1 公平有监督学习

公平有监督学习的研究最初集中于分类任务，并逐渐扩展至推荐、信息检索等领域.分类任务的经典公平定义有基准率公平[55]、准确率公平[56]和校准公平[57]3 种，新的公平定义层出不穷，Narayanan[58]曾总结了21 种不同的公平定义，本节仅对比分析其中常用的6 种.在这6 种定义中，定义4～6 为最常用的公平定义；定义7～9 具有独特的基本思想或适用范围.

定义4.基准率公平（base rate fairness）.给定为二值分类器，A为受保护属性，基准率公平要求：

定义5.准确率公平（accuracy-based fairness）.给定为二值分类器，A为 受保护属性，Y为真实值，准确率公平要求：

准确率公平又被称为机会平等（equal opportunity），在此定义下，受保护的群体与未受保护的群体具有相等的真阳性率和假阴性率.

定义6.校准公平（calibration-based fairness）.给定为分类器，A为 受保护属性，Y为真实值，校准公平要求：

在此定义下，对于任何预测概率η，受保护的群体与未受保护的群体实际属于正例的概率是相等的.

定义4～6 均基于统计意义上的独立或条件独立，随着因果科学的发展，Kusner 等人[59]基于因果推断技术提出反事实公平（counterfactual fairness）的定义，认为在改变受保护属性，并保持其他非因果依赖于受保护属性的因素不变的情况下，若算法的预测结果分布不发生变化，则该算法是公平的.

定义7.反事实公平（counterfactual fairness）.给定为分类器，A为 受保护属性，为受保护属性之外的其余属性.(G,V,F)构 成因果模型，其中 G为外生变量，不由可观测变量集合 V 中的任何变量决定；V为内生变量，V ≡A∪；F为结构方程，将每个内生变量的值表示为 G 和 F中其他变量值的函数.反事实公平要求：

在样本真实标签存在偏见的情况下，反事实公平通过外生变量的计算去除了样本真实标签中的偏见；而准确率公平和校准公平均依赖于样本的真实标签，无法应对此类情况.

定义4～7 均用于判断算法是否公平，但无法衡量算法不公平的程度.针对该问题，Speicher 等人[60]基于广义熵指数对算法不公平程度进行度量.

定义8.广义熵指数（generalized entropy index）.给定bi为个体i在算法决策结果下的收益，b为收益均值，n为总人数，α ∉{0,1}.广义熵指数计算方法为：

广义熵指数可以统一地度量个体与群体层面的不公平，但其缺点在于收益取值依赖于应用场景，不易确定.以保释为例，收益bi的取值如表5 所示.

Table 5 Benefit Value Under Bail Scenario表5 保释场景下的收益取值

目前的公平定义大多仅针对单一受保护属性，如判断算法是否对女性有歧视；针对交叉受保护属性，如判断算法是否对黑人女性有歧视，Foulds 等人[61]借鉴差分隐私的定义提出了差分公平（differential fairness），用公平代价 ε限制算法在不同群体间输出概率的差异.

定义9.ε-差分公平（differential fairness）.给定样本的分布θ，ai,aj为 不同的受保护属性.若分类器满足条件：

在此定义下，无论受保护属性的组合如何，算法输出概率都是相似的.

以上介绍了分类任务中的6 种公平定义，表6 对这6 种公平定义的基本思想和适用范围进行对比分析.首先，在公平类型上，这6 种公平定义中只有反事实公平与广义熵指数支持个体公平，其余均属于群体公平类型；其次，在基本思想上，这6 种公平定义中只有反事实公平是要求受保护属性A与预测结果之间的因果独立，其余均是统计意义上的独立或条件独立；最后，在适用场景上，差分公平适用于交叉受保护属性，广义熵指数与差分公平均可用于衡量算法不公平的程度.

4.2 公平无监督学习

公平无监督学习的研究基于公平有监督学习的众多公平定义进行类比与拓展，主要集中于聚类、主成分分析、异常检测等任务.Chierichetti 等人[62]研究了经典聚类问题中的k-center 和k-median 算法，要求受保护群体在每个聚簇中具有相似的表示，提出如定义10 的公平目标.该目标希望每个聚簇中不同受保护群体所占比例尽可能相等，即当点集Ui中属于群体A的 数据点和属于群体B的数据点相同时，balance(Ui)取得最大值1，即最公平；当Ui中只包含属于单一群体的数据点时，balance(Ui)取得最小值0，即最不公平.Backurs 等人[63]基于和Chierichetti 等人[62]相同的公平目标，将公平聚类算法的时间复杂度从超二次降低为线性.

定义10.平衡（balance）.给定点集U，整数k，U={U1,U2,…,Uk}为 点集U上的一个划分，对于受保护群体GA和GB，Ui⊆U，Ui上的平衡定义为

则划分 U 上的平衡定义为

Ghadiri 等人[65]指出在设施选址问题上，平衡的目标并不是公平的，并提出了社会公平定义.

定义12.社会公平（socially fairness）.给定点集U，整 数k，U={U1,U2,…,Uk}为点集U上的一个划分，Λ={λ1,λ2,…,λk}为聚类中心的集合，聚类算法的代价为

则对于受保护群体GA和GB，社会公平的目标是最小化

表7 对聚类任务的3 种公平定义的基本思想和适用范围进行对比分析.3 种公平定义均属于群体公平类型，其中只有比例性定义的群体划分不依赖于受保护属性.在基本思想上，平衡定义仅考虑聚簇中不同受保护群体的比例；比例性定义考虑聚簇的规模；社会公平考虑数据点到聚簇中心的平均距离.可见，即便任务相同，在不同的应用场景下，公平目标也不同.在群体划分上，比例性定义不依赖于受保护属性.

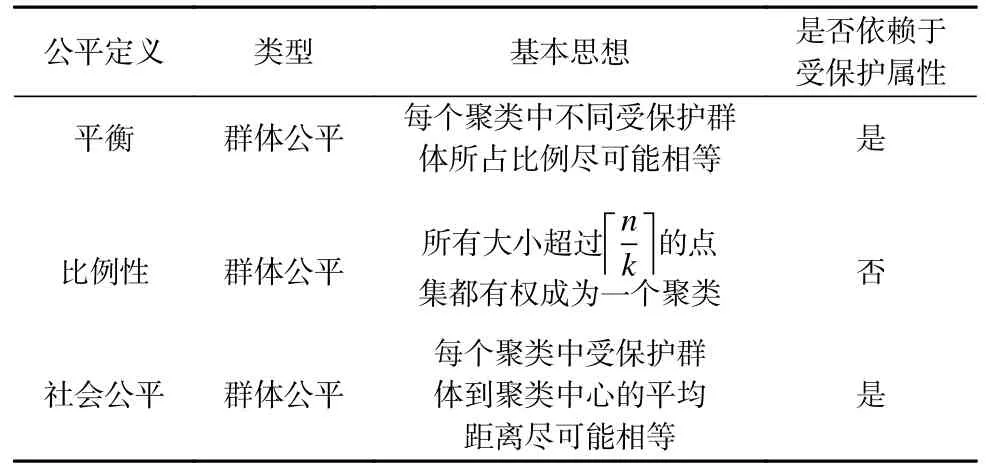
Table 7 Comparative Analysis of Three Definitions of Fairness in Clustering Tasks表7 聚类任务3 种公平定义的对比分析

基于定义12，模型偏见下的算法公平可采取中间处理（in-processing）与后处理（post-processing）这2 种方法进行实现.中间处理是指在模型训练过程中修改训练目标，通常采取公平正则化的方法.如Kamishima 等人[66]基于受保护属性与算法输出的互信息设计了偏见指数，将偏见指数以正则化项的方式引入模型的损失函数中.当偏见指数为0 时即满足统计平等的定义.除了公平正则化外，还有其他的方法致力于修改训练目标.如域独立性学习（domain independent learning，DI）[67]针对受保护属性不同的群体分别训练单独的分类器，然后再集成分类器的输出.组偏移的分布鲁棒性优化（distributionally robust optimization for group shifts，G-DRO）[68]改进了期望风险最小化的目标，通过优化最差组的训练误差，增强模型的泛化性从而改善公平性.后处理是指将模型训练的过程视为黑箱，通过调整模型输出结果来实现公平.如Hardt 等人[56]通过设置阈值机制调整贝叶斯模型的输出结果，从而实现准确率公平.

5 算法公平的评估

为评估不同公平指标的关系与不同公平方法的效果，本节分别从公平指标与公平方法2 个方面对算法公平进行实验.

5.1 公平指标评估

德国信用数据集、银行营销数据集、Adult 数据集、COMPAS 数据集是算法公平的常用数据集.本节基于这4 个数据集，分别对社会偏见、数据偏见以及模型偏见下的算法公平进行实验评估.其中，德国信用数据集与银行营销数据集采用与Kamiran 等人[38]相同的敏感属性设置，以年龄作为敏感属性，将人群分为25 岁及以上（成人）、25 岁以下（青年）2 类群体，同时去除性别属性以及与性别相关的婚姻状态属性（只考虑单一敏感属性）.Adult 数据集与COMPAS 数据集采用种族作为敏感属性.本节将数据集随机拆分为70%的训练集与30%的测试集，分别训练决策树、朴素贝叶斯、逻辑回归、支持向量机（support vector machine，SVM）这4 种传统机器学习模型，以及神经网络模型中的多层感知机（multilayer perceptron，MLP），共计5 种分类模型.模型参数选取scikit-learn 的默认参数.

关于本节对比的公平指标，社会偏见下的算法公平指标参考均衡蛋糕分割的思想，假设样本i对信用评分的估值vi符合正态分布N(0.5,0.25)，表示样本i的 预测标签，A=0 表 示青年群体，A=1表示成人群体，则定义加权基准率公平指标为

数据偏见下的算法公平指标参考基准率公平的定义，采用2 类群体的正例的比例差异进行衡量，定义数据基准率公平为

模型偏见下的算法公平指标参照4.1 节的6 种定义.其中，基准率公平、准确率公平与校准公平均采用概率差值的绝对值进行计算；反事实公平采用反事实操作前后的真阳性率差值的绝对值进行计算；广义熵指数设置参数 α=2；差分公平采用拉普拉斯平滑进行概率估计.

上述公平指标均是数值越小，表示公平性越高.此外，为衡量模型与数据集相比在基准率公平上的改善，定义基准率公平差异为模型基准率公平与数据基准率公平的差值，该指标数值越大，表示模型在基准率公平上的改善越大.针对公平指标，由图3～5分析得到3 条结论.

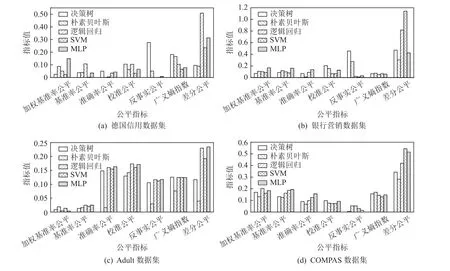
Fig.3 Comparison of fairness indicators of different models图3 不同模型的公平指标对比

1）分类模型在不同公平指标上的表现差异较大.针对各分类模型，计算社会偏见、模型偏见下的算法公平指标对比如图3 所示.可以发现：没有任何一种分类模型可以在7 种公平指标上均表现最佳.如对于德国信用数据集：在准确率公平上，朴素贝叶斯模型表现最好；而在广义熵指数上，朴素贝叶斯模型表现较差.在差分公平上，决策树模型表现较好；而在反事实公平和广义熵指数上，决策树模型均表现最差.在反事实公平上，逻辑回归模型表现最好；而在差分公平上，逻辑回归模型表现较差.

2）在现有模型上，公平性与准确性之间存在权衡关系.如图4 所示，准确率较高的模型在基准率公平上的表现往往较差.例如：在德国信用数据集和银行营销数据集上，准确率最高的逻辑回归模型在基准率公平上的改善较小；在Adult 数据集上，准确率较高的MLP 模型在基准率公平上的改善最小；在COMPAS 数据集上，逻辑回归与SVM 模型在准确率上表现较好，而在基准率公平上表现较差.这体现出公平性与准确性之间的权衡.

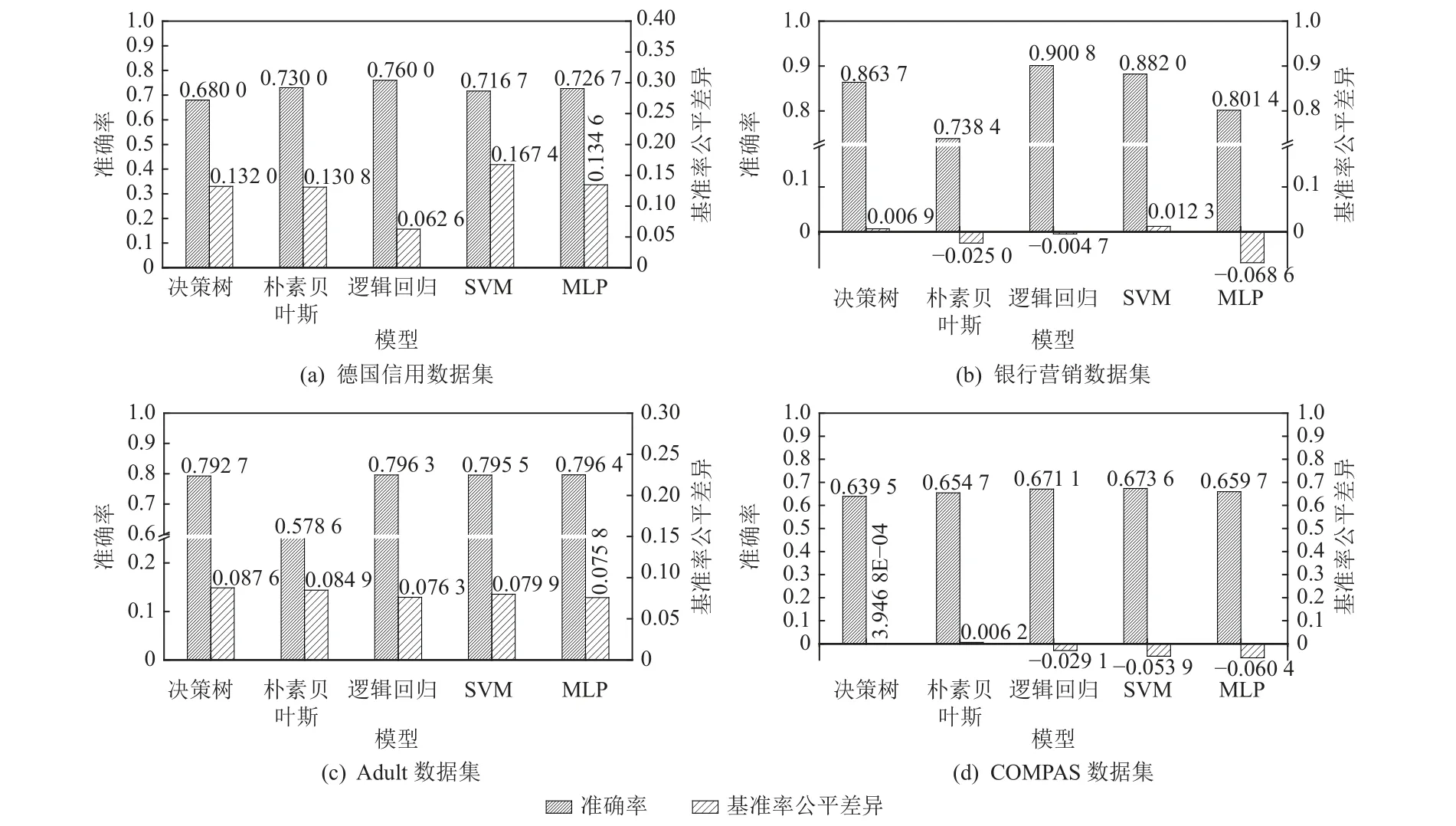
Fig.4 Accuracy and base rate fairness difference of different models图4 不同模型的准确率与基准率公平差异

3）不同公平指标间的相关性差异较大，难以实现共同最优.图5 展示了7 种公平指标之间的皮尔森相关系数热力图.由图5 可知：在这4 个数据集上，广义熵指数与校准公平、反事实公平之间存在一定的正相关性，而与加权基准率公平之间呈现负相关性.此外，公平指标在不同数据集上的相关性并不稳定，如：在德国信用数据集和银行营销数据集上，基准率公平和准确率公平之间呈现负相关关系；而在Adult数据集和COMPAS 数据集上，基准率公平和准确率公平之间呈现正相关关系.这说明在不同的公平指标上难以实现共同最优.

Fig.5 Correlation between fairness indicators图5 公平指标间的相关性

5.2 公平方法评估

为对比不同公平方法的效果，参照Qraitem 等人[69]的实验设置，在数据偏见下的算法公平中，本节选取了过采样（oversampling,OS）、欠采样（undersampling,US）、重赋权（upweighting,UW）这3 种不平衡数据处理方法，以及对抗性训练（adversial training,ADV）[44]、对比学习（bias-contrastive learning，BC）[50]这2 种公平表示学习方法；在模型偏见下的算法公平中，本节选取了DI[67]与G-DRO[68]这2 种中间处理方法进行实验评估.与文献[50,69]保持一致的是：实验数据集选取UTKFace 人脸识别数据集，实验任务以性别为分类目标Y，以种族为受保护属性A；实验控制训练集的偏度，即训练集中Y与A的 相关性P(Y|A)；使用的公平指标为无偏准确率（unbiased accuracy，UA），以分类类别与受保护属性交叉划分子组，UA 定义为所有子组准确率的平均值.与文献[50,69]不同，文献[67-68]仅设置偏度为0.9，本节对比了各公平方法在多个不同偏度下的表现，如图6 所示.

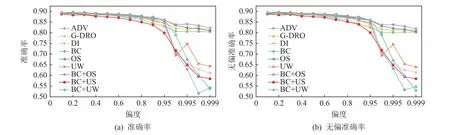
Fig.6 Performance of fair methods under different bias rates图6 各公平方法在不同偏度下的表现

由图6 分析可得3 个结论：

1）在数据集偏度较高时，公平方法的表现并不稳定.当偏度超过0.95 后，各公平方法的公平性与准确性降低幅度都较大.这说明鲁棒的公平方法值得研究.

2）在现有公平方法上，公平性与准确性之间存在一致关系.以无偏准确率作为公平指标和训练目标时，具有较高无偏准确率的模型同样具有较高的准确率.

3）单一的公平方法取得的效果有限.实验比较了将对比学习与3 种不平衡数据处理方法相结合的组合方法，其中对比学习结合过采样（BC+OS）方法在数据集高度有偏的情况下也能取得较好的效果，并优于仅用对比学习的方法和仅用过采样的方法.这说明公平方法的组合值得探索.

6 算法公平计算面临的挑战

如图7 所示，算法公平的3 个维度是相辅相成、相互贯通的.从历史发展的角度来看，社会偏见下的算法公平出现于小数据时代，主要通过博弈论与运筹学实现公平.数据偏见下的算法公平出现于大数据时代，主要通过平衡数据分布与表示学习实现公平.模型偏见下的算法公平出现于人工智能时代，主要通过正则化与后处理实现公平.秉承莱布尼茨的“思维可计算”思想，本文认为实现算法公平的过程本质上是一个计算过程，因此本文将实现算法公平的方法称为“公平计算”.

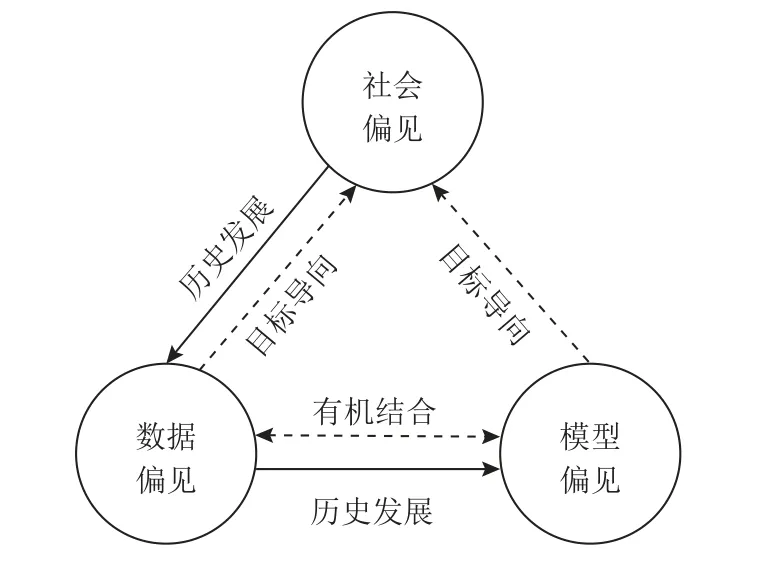
Fig.7 Relationship among the three dimensions of algorithmic fairness图7 算法公平3 个维度的联系

从事物联系的角度来看，社会偏见下的算法公平是指引公平计算方法的目标方向.公平问题的本质是社会问题.作为公平问题的分支，算法公平必然具有社会性，其最高目标是以人为本实现社会总福利的帕累托最优.

数据偏见下的算法公平是公平计算方法的基础前提.有偏见的数据输入算法会产生有偏见的输出，当算法的输入输出形成闭环时，更会引发偏见的恶性循环.由于样本量不足或预测变量未测量等原因导致的偏见应首先通过数据收集来解决，而不是直接对模型进行约束[70].

模型偏见下的算法公平是公平计算方法的强化手段.算法公平问题的复杂性决定了单一的公平计算方法的疗效有限，即便数据层消除了偏见，模型层也可能由不合理的目标函数带来偏见，如Kilby[52]针对机器学习预测阿片类药物使用风险评分与使用阿片类药物的个体异质性治疗效果并不相关的实验结果进行分析研究，指出在医疗保健场景下研究人员对目标函数的选择也是算法偏见的来源.因此，算法公平问题的解决方案应有机结合数据偏见下的算法公平与模型偏见下的算法公平，并力求接近社会偏见下的算法公平.

综上所述，本文提出如图8 所示的算法公平计算框架.该框架包含公平定义量化、公平监测预警以及公平方法选择3 个模块.其中，公平定义量化模块基于各类公平定义，针对不同类型的数据及模型进行公平度量值计算，如针对模型结果r，计算得到公平指标i的数值为Fi(r).然后，基于计算出的公平度量值，公平监测模块针对风险数据进行预警，利用法律法规进行处罚.在第5 节的实验部分可发现，公平指标在不同数据集上的差异性较大，仅通过指标计算结果难以解释分析歧视来源.因此，该模块要求数据提供者和服务提供商借助算法追索技术[71]提供解释.算法追索技术是一种可解释技术，例如某用户未获得贷款，算法追索技术需要告知用户想要获取贷款应如何去做（如将资产提升至20 万元）.最后，公平方法选择模块为计算出的每个公平指标赋予不同的权重，形成统一的权衡函数.该模块基于权衡函数，在已有公平计算方法库中选择适当的公平计算方法，从而进行公平上的改进.在社会偏见下的算法公平中，本文介绍了公平利益分配与公平损失分摊2 类问题，这2 类问题可用博弈论与运筹优化方法解决；在数据偏见下的算法公平中，本文介绍了显式偏见与隐式偏见2 类问题，这2 类问题分别可用不平衡数据处理与公平表示学习方法解决；在模型偏见下的算法公平中，本文介绍了公平有监督学习与公平无监督学习2 类问题，这2 类问题可用中间处理和后处理方法解决.

下面对算法公平计算面临的挑战和未来研究方向进行分析展望.

1）公平度量标准的选择

目前，尚无统一普适的公平度量.Kleinberg 等人[72]证明了除了在高度约束的特殊情况下，无法同时满足3 种不同的公平度量，即不同的公平度量基本互不相容.由第5 节实验可知，一个模型在某种公平度量上表现良好，可能在其他公平度量上表现极差.因此，如何针对特定领域选择合适的公平度量仍有待厘清.比如在医疗领域的疾病诊断算法，如果算法预测的男性和女性的发病率不同是否意味着不公平？

2）公平与其他指标的关系

在不考虑算法准确性的情况下，很容易实现算法公平性，但这会使算法失去实际应用价值.因此，我们希望在算法保证足够准确的基础上尽可能地达到公平.但由于数据偏见与模型偏见的复杂性，实现算法公平通常会对算法准确性造成伤害.除了算法准确性，隐私性与算法公平之间也存在相互作用.例如，差分隐私是目前隐私保护的常用技术，通过向原始数据中添加噪声扰动的方式实现难以区分个人隐私数据的目的.Pujol 等人[73]针对差分隐私在投票权分配、联邦资金分配和议会代表分配3 类场景中的应用进行研究，发现在严格的隐私约束（较小的ε）下，为实现隐私而添加的噪声可能会对某些群体产生不成比例的影响.类似地，Suriyakumar 等人[74]针对差分隐私在医疗保健场景的应用进行研究，发现差分隐私引入的随机噪声可能偏向于影响数据分布长尾（即少数群体）的准确性.除了隐私与公平之间的权衡关系外，Tian 等人[75]指出隐私保护与公平保护之间存在交集，如隐私保护关注的敏感属性与公平保护关注的受保护属性一致，则消除特征表示中的敏感信息可同时保障隐私性与公平性.因此，如何在算法公平与其他指标间进行权衡，以及算法公平与其他指标之间具有怎样的相互作用仍有待研究.

3）鲁棒的公平计算方法

目前的公平计算方法鲁棒性并不强，研究发现，数据集中存在的噪声会影响算法公平计算方法的有效性.例如Mehrotra 等人[76]针对子集选择算法的公平性进行研究，发现在受保护属性存在噪声的情况下，直接施加公平约束反而会降低算法公平性；Wang等人[77]在样本标签含有噪声的场景下，针对分类算法的公平性进行研究，得出了类似的结论.此外，Khani 等人[78]发现由于模型的归纳偏置，删除伪特征会降低模型准确性，并对不同的群体产生不同比例的影响.因此，鲁棒的公平计算方法是有挑战的研究方向.

4）算法公平的非技术解决方案

目前，算法公平的相关研究大多没有分析算法不公平的实际危害，试图通过技术手段解决一切算法公平问题，然而某些场景下可能存在更好的非技术解决方案.比如：谷歌翻译将土耳其语、匈牙利语等性别中立的语言（即没有区分性别的人称代词）翻译成英语时，将女性与“漂亮”“家务”“护士”等词语关联起来，将男性与“聪明”“赚钱”“医生”等词语关联起来.针对此类性别刻板印象问题，技术上可以采用公平表示学习的方式将性别与刻板印象解相关；产品设计层面则可以允许用户选择将没有区分性别的人称代词翻译成男性、女性或其他性别.类似地，Albert 等人[79]针对智能体重秤的身体成分分析依赖于二元性别作为输入，对于变性人等性少数群体不适用的问题，提出了2 类改进建议：技术上，在输入变量中去除性别以及与性别相关的信息；非技术上，为性少数群体增加二元性别之外的其他选项.因此，算法公平作为交叉领域的研究问题，如何在特定场景下选择适合的学科理论方法仍有待研究.

5）公平计算的工具

针对偏见的检测与消除，IBM[80]、微软[81]、谷歌[82]等公司开发了公平计算的相关工具.IBM 开发了AI Fairness 360[80]工具包，它支持Python 与R 这2 种语言，涵盖多种公平度量指标与去偏算法.微软开发了Fairlearn[81]工具包，它支持Python 语言，提供公平度量、偏见消除及绘图等功能.谷歌开发了Fairness Indicators 工具包，该工具包涵盖分类任务的常用公平度量，以可视化的形式提供数据评估与模型分析，并且适用于大规模数据集.此外，针对算法公平的长期性与动态性，谷歌还推出了ML-fairness-gym[82]，并在银行贷款、注意力分配和大学录取这3 类动态场景下进行验证.尽管已有公平计算相关工具，但现有的公平计算工具主要面向分类任务，社区生态尚不完善，针对其他任务的公平计算工具仍有待开发.

7 结束语

算法公平问题备受关注，但作为计算机科学与社会科学的交叉问题，不仅要继承社会科学各领域的基本理论，更要从定性分析转向定量计算.基于此，本文强调算法公平问题需要具备公平计算的方法与能力.本文首先对算法公平问题的发展脉络进行梳理，将其根源分为社会偏见、数据偏见、模型偏见3个阶段；然后分别对3 类偏见下的算法公平计算方法进行总结归纳，并通过实验进行对比评估；最后，提出了算法公平计算框架，并对面临的挑战与未来研究方向进行展望.

作者贡献声明：范卓娅负责完成实验并撰写论文初稿；孟小峰提出指导意见并修改论文.