面向大规模数据的DBSCAN 加速算法综述

陈叶旺 曹海露 陈 谊 康 昭 雷 震 杜吉祥,6

1（华侨大学计算机科学与技术学院 福建厦门 361021）

2（食品安全大数据技术北京市重点实验室（北京工商大学）北京 100048）

3（电子科技大学计算机科学与工程学院 成都 611731）

4（模式识别国家重点实验室（中国科学院自动化所）北京 100190）

5（厦门市数据安全与区块链技术重点实验室（华侨大学）福建厦门 361021）

6（福建省大数据智能与安全重点实验室（华侨大学）福建厦门 361021）

7（江苏省计算机信息处理技术重点实验室（苏州大学）江苏苏州 215006）

（ywchen@hqu.edu.cn）

大数据时代，数据信息呈爆炸式增长，如何从海量的信息中提取隐含在其中的有效信息，并进行分析与预测未来的发展趋势和模式是信息技术领域的重要课题.因而，数十年来，数据挖掘、机器学习、深度学习等相关技术不断推陈出新，取得了长足的进展，结出了丰硕的成果.

然而，许多相关技术和算法需要大量的有标签数据来进行学习和训练.面对大数据，人为的标记将耗费大量的时间与人工成本.因此，作为无监督学习中能自动地对数据进行分类的聚类算法，成为解决样本标记难等问题的重要手段.

聚类算法是数据挖掘、模式识别、机器学习等领域的基础算法，可以作为一个独立的工具进行数据的相似性度量，观察数据的分布情况，对每一簇数据进行进一步分析，将数据进行划分.聚类算法已经在众多领域有具体应用案例，如在异常检测、数据挖掘、图像处理等领域.

至今为止，聚类算法的研究一直是科研人员的研究热点.经典的聚类算法有层次化聚类、基于图聚类、基于密度聚类、基于网格聚类、基于模型聚类等.但在聚类算法中依然存在不少挑战，如针对特征值缺失的数据进行聚类、对大规模数据进行聚类、对高维数据进行聚类等一直是现实中面临的难题.

DBSCAN（density-based spatial clustering of applications with noise）算法是Ester 等人[1]于1996 年提出的算法.该算法是一种典型的基于密度的算法，用于发现任意形状的聚类以及检测异常值.与常见的k-means 算法[2]相比，DBSCAN 不需要事先划分好簇，只需要输入参数ε（指定邻域半径）和MinPts（邻域密度阈值）就可以将紧密相连的数据划为一类.该算法从问世至今，在理论和实践中都受到广泛关注，并于2014 年在ACM 大会上获得the Test of Time 奖.

然而，DBSCAN 也存在众多不足：1）时间复杂度较高，对大规模数据集进行聚类代价过大；2）参数难以确定，调整困难；3）不适应高维数据，对高维数据聚类效果不佳；4）无法对多密度数据进行聚类等.其中该算法复杂度过大，难以对大数据进行有效处理严重阻碍了其在工业界的应用.

分析表明，DBSCAN 复杂度过大主要原因在于需要双重循环对所有数据点进行欧氏距离计算，对每个数据点找出给定邻域内的近邻，其间存在着大量的冗余.如何有效地过滤冗余的计算，对DBSCAN进行加速，使之能处理大规模数据，成为近年来的一个研究热点.

为此，许多学者分别从不同的技术角度加速DBSCAN，取得了不少进展.从这些算法的加速手段所针对的目标划分，可以分为减少冗余计算和并行化两大类.但从具体的加速手段上来看，本文从这些工作的基本原理出发，按3 点规则对这些进展进行分类：1）是否硬件加速；2）加速结果是否为近似解；3）按何种方式减少冗余距离计算.

按上述3 点规则，本文主要针对近年来DBSCAN算法的快速化工作进行了整理与分析.就具体的加速技术而言，现有的算法主要分为6 种类别：基于分布式、基于采样、基于近似模糊、基于快速近邻、基于空间划分、基于GPU 加速等技术.图1（a）主要展示了这些加速工作的发展历程，列出了这6 种主要类别的代表性方法.其中，有许多方法融合了多重技术，分别在DBSCAN 的不同阶段进行加速.比如：分布式技术常与空间划分技术相结合，快速近邻技术常与近似模糊技术、空间划分技术相融合等.图1（b）展示了多重加速算法的主要技术手段.

Fig.1 Summary of fast DBSCAN algorithms图1 快速化DBSCAN 算法汇总图

我们对本文中使用的主要变量和符号进行整理，如表1 所示.

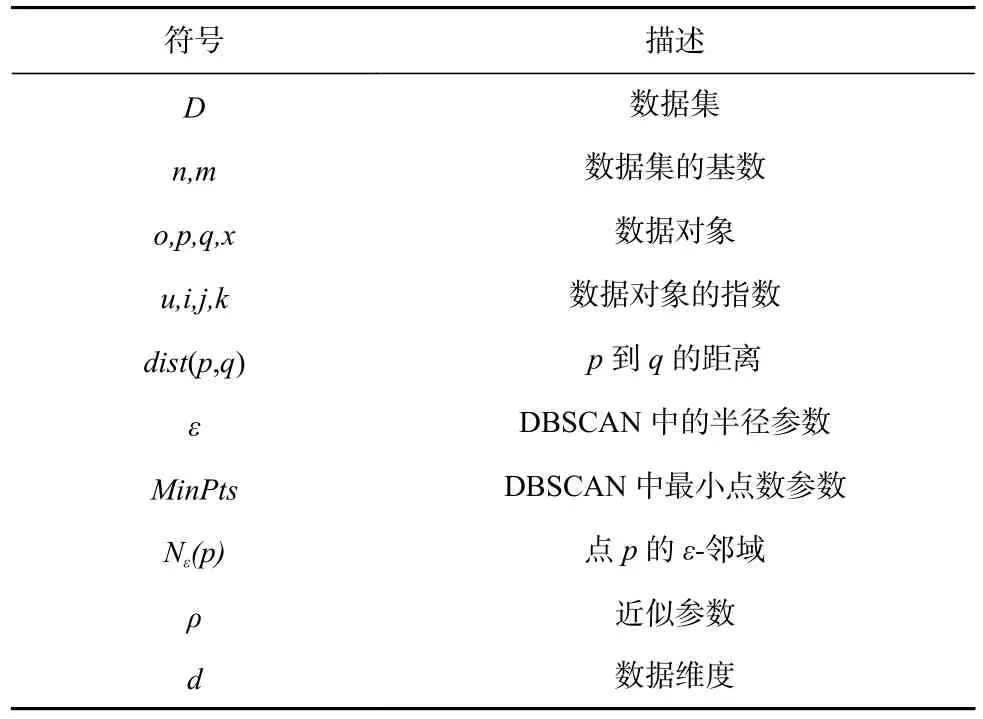
Table 1 Description of Main Variables and Symbols Used in the Paper表1 本文中使用的主要变量和符号的描述

1 DBSCAN 的发展历史、符号、定义

DBSCAN 是依赖于基于密度的聚类概念，旨在发现任意形状的聚类.有关DBSCAN 的7 个重要概念定义如下：

定义1.对p∈D，数据集D中与p的距离小于ε的数据，即Nε(p)={q∈D|dist(p,q)≤ε}，称为p的ε-邻域，其中，dist(p,q)=‖p-q‖2.

定义2.若 |Nε(p)|≥MinPts，则称数据点p为核心点，其中MinPts为预先定义的自然数阈值.

定义3.若p∈Nε(q)且 |Nε(q)|≥MinPts，则称数据点p从数据点q密度直达.

定义4.若存在点p1,p2,…,pn,p1=q,pn=p，对于序列中任意一个点pi，使得pi+1从pi密度直达，则称数据点p从数据点q密度可达.

定义5.若存在数据点o，使得点p和点q都能从点o密度可达，则称数据点p与数据点q密度相连.

图2 展示了密度直达、可达、相连定义图，依据定义2～5.x为核心点，y由x密度直达，z由x密度可达.o为核心点，点p，q分别由点o密度可达，则p与q密度相连.

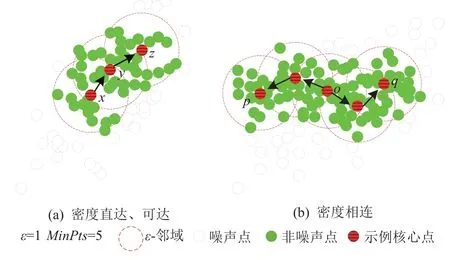
Fig.2 Definition diagram of density direct,accessible,connected图2 密度直达、可达、相连定义图

定义6.若q为非核心点，∃p∈D满足p为核心点且q∈Nε(p)，则称q为边界点.

定义7.假设数据集D被聚类为k个类簇集C1,C2,…,Ck，若p不属于任何类别，即 ∀i:p∉Ci，称p为噪声点.所有噪声点构成噪声集，即noise={p∈D|∀i:p∉Ci}.

根据上述核心点、边界点以及噪声点的定义，在图3 中进行了展示.

Fig.3 Classification of core points,boundary points,outlier points图3 核心点、边界点、噪音点的分类

2 基于分布式的加速改进

在数据规模非常大的今天，即使是最简单的数据分析任务也可能超过任何一台机器的处理能力.像其他同类型算法一样，DBSCAN 具有计算成本高、当数据无法装入内存时I/O 速度变慢等问题.因此，很有必要并行执行DBSCAN 以减少处理时间.MapReduce 和Spark 是2 种非常重要的并行处理数据框架.MapReduce 具有可伸缩、高度并行化和抽象化的优点.Spark 框架除了拥有MapReduce 所有的重要特性外，它还具有一些新特性，在Spark 中，RDD（resiliennt distributed datasets）允许程序员在聚类上执行内存计算且支持流数据、复杂分析、实时分析.

PDBSCAN[3]（parallel DBSCAN）是最早的分布式DBSCAN，该算法采用分布式空间索引结构dR*-Tree实现分布式并行化，具有近乎线性的加速，但是其如今的数据规模已经远远超过了当时的数据量.

Patwary 等人[4]则指出PDBSCAN 采用类似于主从模式的方法，导致主服务器和从服务器之间的通信开销很大，并且在合并过程中并行效率很低.因此，提出了PDSDBSCAN（parallel DBSCAN using disjointset）.该算法最初为数据集的每个点创建一个单节点树，然后使用disjoint-set[5]数据结构对属于同一簇的树进行合并，直到发现所有簇为止，合并可以按照任意顺序执行.这打破了固有的数据访问顺序，实现了高数据并行，其性能显著优于主从方法.

MR-DBSCAN[6]（MapReduce-DBSCAN）算法先计算数据的大小以及一般的空间分布，以生成一个维度索引列表.然后根据分区配置文件，对子空间进行划分.在最后阶段合并子空间时处理跨边界问题，它将从边界子空间中找出2 个簇对的列表，以便为每个边界合并.MR-DBSCAN 的执行时间随数据大小的增加而缓慢增加.但是这个算法不能正确地平衡并行任务之间的负载，尤其是在数据严重倾斜的情况下.

为此，在MR-DBSCAN 算法的基础上，提出了一种基于CBP（cost-based partitioning）的方法[7]，以实现对严重倾斜数据的负载均衡.该算法首先执行一个MapReduce 作业来收集数据分布的统计信息.在Shuffle 阶段，这些点按它所属的单元分组，Reduce 函数生成一个概要文件，记录每个单元中的点数，根据统计数据分布估计的计算代价来计算最小完全划分集.分区结束后，开始进行局部聚类，为了实现对邻域的高效查询，用R-Tree[8]在聚类之前索引分区中的所有点.对于每个分区，将全局合并阶段涉及的点输出到2 个单独的文件中，建立局部聚类到全局聚类的映射.最后调整局部聚类的中间结果，将局部聚类替换为全局聚类，从而得到最终结果.该算法在空间数据集非常不均匀、严重倾斜的情况下能够很好地聚类并且对大规模数据集有良好的加速性能.

为解决数据分区之间的负载不平衡，Song 等人[9]则开发了一种新颖的并行DBSCAN 算法，即RPDBSCAN（random partitioning-DBSCAN）.该算法将伪随机分区与2 级单元字典一起使用，找到每个数据分区的局部聚类，然后合并这些局部聚类以获得全局聚类.算法的整体流程如图4 所示，整个算法可以分为3 个阶段：阶段1 为数据划分，首先执行伪随机分区P，如图4 左上角的图所示，整个数据空间被划分为这些单元格，空区域不创建任何单元格，这些单元被分配到P1和P2这2 个不同的分区.阶段2 创建核心图，使用2 级单元字典，对每个分区中存在的所有内部单元执行区域查询，以区分核心和非核心单元.例如，如果确定图4“数据分区”图中的Cnc1到Cnc5为非核心（C表示数据点单元），则将这些非核心单元排除在外.然后通过从每个分区的每个核心单元中搜索所有完全或部分直接可达的单元来构造核心图.在图4“单元构建”图中，图中单元之间的有向边表示2 个单元完全或部分直接可达.阶段3 执行全局聚类，该算法会合并所有图并确认每个边是否指示完全或部分直接可达的关系，然后，基于此合并图扩展聚类.在图4“单元合并”图中，群集Q1（Q表示点集）由位于P1和P2左下角的单元形成.经过空间划分、单元构建与合并这3 个阶段，RP-DBSCAN实现了完美的负载平衡，其性能远远高于此前的同类法[1,5,7]，此外，RP-DBSCAN 能够处理的数据量高达362 GB，提高了DBSCAN 算法在大数据时代的可用性.

Fig.4 The overall flow of RP-DBSCAN[9]图4 RP-DBSCAN 的整体流程[9]

除此之外，还有不少基于分布式的DBSCAN.如DBSCAN-MR[10]，MR-IDBSCAN[11]，RDD-DBSCAN[12]，SDBSCAN[13].在DBSCAN-MR[10]（reduce-based partition DBSCAN）中，算法可以在云上执行，不需要全局索引，但是分区机制会影响每个节点的执行效率和负载均衡.因此，提出了减少边界点的分区方法来提高每个节点的执行效率和负载均衡.MR-IDBSCAN[11]（MR-incremental DBSCAN）则是将增量DBSCAN 嵌入到MapReduce 分布式框架中以降低运行时的复杂性.Cordova 等人[12]提出了RDD-DBSCAN，该算法为了均匀分割数据空间，采用二进制空间分区，递归地将所需空间划分为代价大致相等的区域，从而提高了速度.大多数分布式并行化DBSCAN 几乎都是针对2 维数据进行聚类.这是因为随着数据维数的增加，高维空间的拆分和整合将消耗大量的时间.为了解决这一问题，Luo 等人[13]提出了S-DBSCAN（DBSCAN on Spark），该算法通过质心对数据分区进行合并，从而提高了高维数据聚类的效率.

Lulli 等人[14]提出的NG-DBSCAN（neighbor graph DBSCAN）同样能够对高维数据集进行良好聚类.该算法是一种近似的基于密度的聚类算法，可以对任意数据和任何对称距离度量进行操作.这一算法的分布式设计使其可扩展到非常大的数据集，它的近似特性使它快速产生高质量的聚类结果.算法分2 个阶段进行：第1 阶段创建了空间图，将用于避免空间邻域查询；第2 阶段以空间图作为输入，计算类别.结果表明，NG-DBSCAN 即使是在大的、高维的或任意数据的情况下也能够高效地近似DBSCAN.

Han 等人[15]利用新的大数据框架Spark，提出了一种新的并行DBSCAN 算法.为了减少搜索时间，在算法中使用了Kd-tree[16].利用队列来包含数据点的邻居，在检查和处理数据点时使用Hash 表.此外，还使用了Spark 的其他高级特性来提高效率.结果表明，该算法在高维数据集下实现良好的加速.

在并行KNN-DBSCAN[17]（k-nearest neighbor DBSCAN）中，算法使用OpenMP（open multi-processing）共享内存和MPI（massage passing interface）分布式内存实现并行化.这使得算法可以在不到1 s 的时间内聚类10 亿个3 维的数据点，还能够对上百亿个20 维的数据开展聚类.证实了该算法无论是在高维还是低维的情况下都能展开聚类.

表2 对上述基于分布式技术的DBSCAN 加速算法进行了梳理.分布式技术能够高效地聚类大规模数据，甚至是上亿规模的数据[4,6-7,9,17]，但对于严重倾斜的数据，平衡并行任务之间的负载是关键问题[7-10].大多数分布式算法关注低维数据聚类[3,6-7,10-13]，只有少数算法能够处理高维数据集[4,9,15,17]，其原因是高维数据巨大的复杂性和难处理性.在并行算法的基础上，若算法是近似的则能够处理任意维度的数据集，由此可见近似性的优越之处.

Table 2 Distribution Based DBSCAN Acceleration Algorithm表2 基于分布式的DBSCAN 加速算法

3 基于采样技术的加速改进

DBSCAN 拥有良好的聚类效果且能够有效地处理噪声，但它需要对整个数据集进行双重循环检测，内存支持量高.DBSCAN 从1 个核心对象p开始扩展1 个类别，它通过对p邻域中每个对象执行邻域查询来扩展，但是p中对象的邻域会互相相交.假设q是p邻域中的1 个对象，如果q的邻域被p中其他对象的邻域所覆盖，则可以省略对q的邻域查询操作，这意味着q不需要被选择作为簇扩展的种子.因此，可以减少q的邻域查询操作消耗的时间和存储q作为核心对象的内存需求.

IDBSCAN[18]（improved DBSCAN）基于此想法，通过对一些代表性对象进行采样，而不是将核心对象邻近的所有对象都作为新的种子，从而降低内存使用量和I/O 代价，加快DBSCAN 算法的速度.IDBSCAN选取8 个不同的点作为MBO（marked boundary object），如图5 所示.对于每一个MBO，都将找到与对象P相邻且最接近的对象作为一颗种子.如果同一点被识别为多个MBO 的最近点，那么这个点只能被视为种子1 次.因此，1 次最多有8 个点是种子，这个数字小于DBSCAN 中的对应数量.IDBSCAN 的时间复杂度可以控制在O（nlogn），不过，IDBSCAN 中MBO 的采样将不必要的点分配给种子会导致执行冗余，影响执行时间.

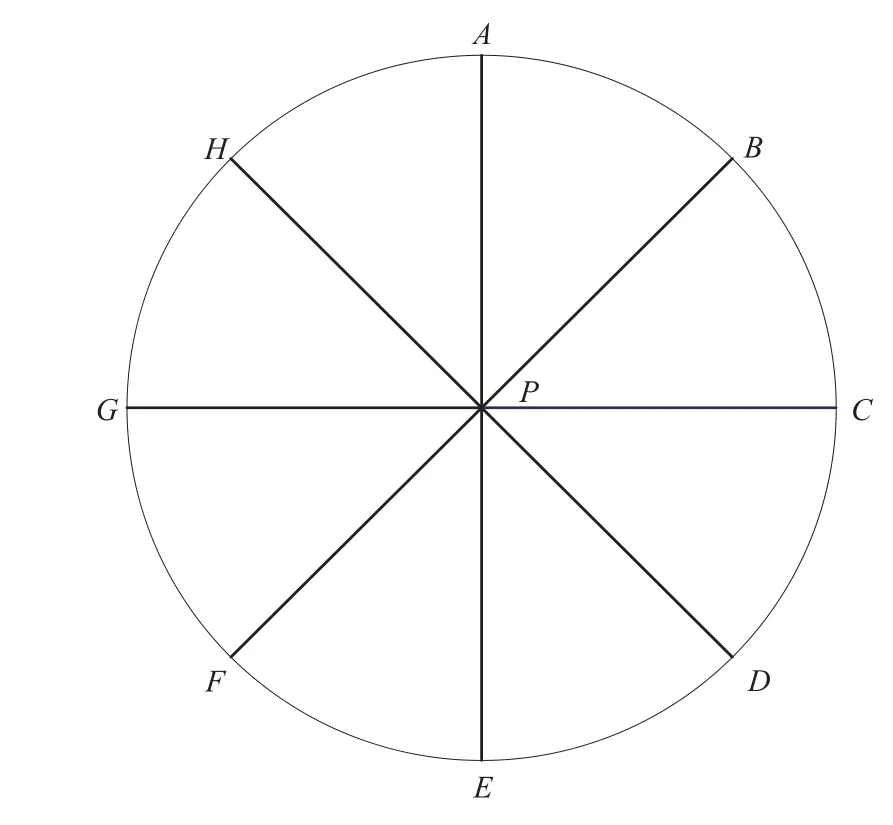
Fig.5 Eight different points on the circle[15]图5 圆上8 个不同的点[15]

基于此，Tsai 等人[19]提出了KIDBSCAN（k-means IDBSCAN），利用k-means[2]对高密度中心点快速定位，再使用IDBSCAN 从这些高密度中心点展开聚类，减少冗余步骤.KIDBSCAN 提高了聚类结果的准确性，同时降低了I/O 成本，其性能优于IDBSCAN.

QIDBSCAN[20]（quick IDBSCAN）则使用 4 个MBO 直接扩展计算.不选择数据点的扩展会增加计算成本，但也会提高速度，因此，QIDBSCAN 的速度明显快于IDBSCAN.

l-DBSCAN（leaders DBSCAN）[21]是一种混合聚类算法，其原型是使用leaders 聚类方法派生的.leaders 工作方式为：给定一个距离阈值τ，对于领导集L，初始为空，并以增量的方式构建.对于数据集D中的每个模式x，如果有一个leader，l∈L且 ||l-x||≤τ，那么x分配给l所属的类别，这时x称为l的追随者.如果没有这样的leader，那么x本身就会成为一个leader，加入到L中.通过这种方法，l-DBSCAN 可以找到与DBSCAN 相同的聚类结果，但所花费的时间要比DBSCAN 短得多.

Rough-DBSCAN[22]也是一种混合聚类技术.该算法首先应用leaders 聚类方法从数据集中导出原型，与原型一起保存密度信息；然后使用leader 来导出基于密度的聚类.此外，Rough-DBSCAN 还增加了一个计数值用于统计leader 的数量，从而可以估算密度.这一技术的时间复杂度仅为O（n）.然而，Rough-DBSCAN 算法的不足之处是会产生密度错误，因此Luchi 等人[23]提出Rough*-DBSCAN.Rough*-DBSCAN密度根据与每个leader 相关联的元素数量来估计，可以获得更好的结果.而Rough-DBSCAN 密度是根据算法返回的每个聚类中的元素数量来计算的，会导致聚类效果不佳.此外，研究人员还提出了一个启发式的算法来为DBSCAN 进行采样，称为I-DBSCAN[23]（intersection DBSCAN）.该算法主要通过找到在球体交点的元素来展开聚类，I-DBSCAN 不需要附加任何参数，只需要原始算法中的 ε和MinPts即可且速度非常快.

DBSCAN++[24]先在数据集X中选择m个均匀采样点来组成子集S，然后计算S中点的密度.确定核心点后，将其余未标记的点聚类到离它们最近的核心点.选择子集的时候，可以使用K中心[25]找到大小为m的子集，使X中任意点到子集最近点的最大距离最小化.换句话说，它试图找到样本点的最有效覆盖.DBSCAN++的时间复杂度为O（nm），其中m的值是子集数，m≪n.

SNG-DBSCAN[26]（subsampledε-neighborhood graph DBBSCAN）是DBSCAN 的简单变体，算法基于一个下采样的邻域图，只需要查询点对的相似度.初始化图的顶点为数据点，对所有数据点对进行采样，如果点对小于ε，则添加到图的边缘部分，处理图的剩余阶段与DBSCAN 相同.SNG-DBSCAN 的时间复杂度可达到O（nlogn），在保持聚类质量的同时能够很好地节省计算资源.

结合前文可知，IDBSCAN 是最早将DBSCAN 和采样技术相结合的算法，KIDBSCAN 和QIDBSCAN都是在IDBSCAN 的基础上改进的算法，但这3 种算法都只针对2 维数据.其他几种基于采样技术的算法能够有效降低DBSCAN 的时间复杂度，处理的数据维度较高，但能处理的数据量有限.

4 基于近似模糊的加速改进

由于精确聚类太过耗时，研究人员对近似方法产生了兴趣，尝试使用近似模糊的思想来提高DBSCAN 的性能.近似意味着聚类结果可能不同于原始DBSCAN 的结果.比如在原始DBSCAN 中，一个数据点p可以被分类到一个簇中，而近似的DBSCAN可以被指定到另一个类别中.

Brecheisen 等人[27]使用OPTICS 计算的枚举对数据进行分区，使得相似的对象具有相邻的枚举值，再通过将多步骤查询处理范式直接集成到聚类算法中.NG-DBSCAN[14]是一种高效的近似算法，其时间复杂度为O（ρnk2），其中k为近邻数，参数ρ和k的取值都很小（ρ=3 和k=10），故计算成本主要由n主导.

AA-DBSCAN[28]（approximate adaptive DBSCAN）使用近似自适应ε距离来确定最小化参数所需要的额外成本计算，同时可以找到具有变化密度的簇.更具体地说，AA-DBSCAN 基于4 叉树将3 维数据集划分为均匀的单元，并创建密度层树，形成了一个由稀疏到密集的不同密度区域构成的数据集，从而能够找到不同密度的簇.该算法在聚类性能和运行时间上都有所提高.

ρ-Approximate DBSCAN[29]也是一种近似DBSCAN算法，并且时间复杂度可以控制在线性时间内.Gan等人[29]证明了在维度大于等于3 时，DBSCAN 问题需要O（n4/3）来解决，解释了原有算法中DBSCAN 可以达到O（nlogn）时间复杂度的说法是错误的，认为ρ-Approximate DBSCAN 的概念将代替DBSCAN.

Schubert 等人[30]肯定了Gan 等人[29]的观察，即在索引结构的支持下，DBSCAN 算法的时间复杂度可达到O（nlogn）的说法是不正确的.但也指出在文献[29]中包含了误导的陈述，如“在限定欧氏距离的条件下，所有的DBSCAN 都是难以忍受的缓慢”.但实际上，DBSCAN 原文[1]中清楚地表明该算法适用于任何距离.原始的DBSCAN 通过有效的指标合理地选择参数，其性能不输ρ-Approximate DBSCAN.因此对于ρ-Approximate DBSCAN 将取代大数据上的DBSCAN 提出了质疑.

Chen 等人[31]提出2 种简单而快速的近似DBSCAN算法：1）KNN-BLOCK DBSCAN 使用快速近似KNN算法来识别核心块、非核心块和噪音块.2）BLOCKDBSCAN[32]使用快速近似算法判断2 个内核块是否彼此密度可达.2 种算法都能高效地近似DBSCAN.

根据图1 多重技术算法汇总表可知，近似技术通常不单独作为一种加速技术，多作为其他加速技术的辅助，如分布式技术、空间划分技术以及快速近邻技术.由于近似技术不追求精确的聚类，当与其他技术相结合时，算法的性能可以显著提高，这也是近似技术的一个强大优势.

5 基于快速近邻的加速改进

近邻搜索是在点集当中搜索点的最近邻居，是许多研究邻域一个重要而广泛的问题，不少科研人员都在这一邻域有所研究[33-38].快速近邻在空间数据库、信息检索、数据挖掘、模式识别等领域都有广泛的应用[39-41].将近邻搜索技术与DBSCAN 算法相结合，可以有效提高DBSCAN 算法的性能.

LSH-DBSCAN（locality-sensitive hashing DBSCAN）[42]最近邻搜索是通过Hash 优化[33]来实现的.其原理是通过建立多个Hash 函数将原始数据点映射到Hash 表，映射过程需要满足映射后相似距离的原始数据仍然相似.算法的时间复杂度为O（N·KlogC）（N为数据量，K为每个Hash 表的维度，C为聚类数），尽管该算法可以在线性时间复杂度下有效地降低数据维数并执行最近邻查询，但缺点是参数增加并且参数难以确定.

Li[43]发现DBSCAN 使用暴力查询来检索每个点的邻居，使得聚类过程中存在很多冗余的距离计算.因此提出了一种改进的基于邻域相似度的DBSCAN算法（neighbor similarity DBSCAN，NS-DBSCAN）.该算法认为一个点应该与它的邻居有相似的密度，因此，使用三角不等式对许多不必要的距离计算进行过滤.算法还使用Cover Tree[34]并行检索每个查询点的最近邻居，从而识别出全局数据中核心点、边界点、离群点.使用三角不等式、近邻相似度、快速近邻搜索等算法，可以极大地减少聚类过程中距离计算的次数，有效地提高了DBSCAN 算法的效率.

邻居的邻居也有可能是邻居这一思想在NQDBSCAN（neighbor query DBSCAN）[44]算法中也有体现.该算法利用邻域搜索技术和索引技术来过滤掉大量不必要的密度计算.其基本思想是：当点p和点q很接近时，p和q应该有相似的邻居.给定参数ε，2点离得越近，近邻越相似.如图6 所示，图6（a）中的p和q比图6（b）中的p和q拥有更多相似的邻居.NQDBSCAN 利用这一思想，有效地减少了大量不必要的距离计算，并且在索引技术的帮助下该算法的平均时间复杂度为O（nlogn）.

Fig.6 Diagram of p and q similar neighbors[44]图6 p，q 相似近邻点图[44]

Chen 等人[31]发现，DBSCAN 中识别每个点的类型本质上是KNN 问题，并且一个点的密度分布和它的相邻点相似.这意味着一个点极有可能具有与其邻近点相同的类型.基于此发现，研究人员首先使用FLANN[35]（fast library for approximate nearest neighbors）来检测所有点中的块.算法的时间复杂度如表3 所示，其中 β为数据分布因子，L为FLANN 中检测的点数，χ为FLANN 的分支因子.

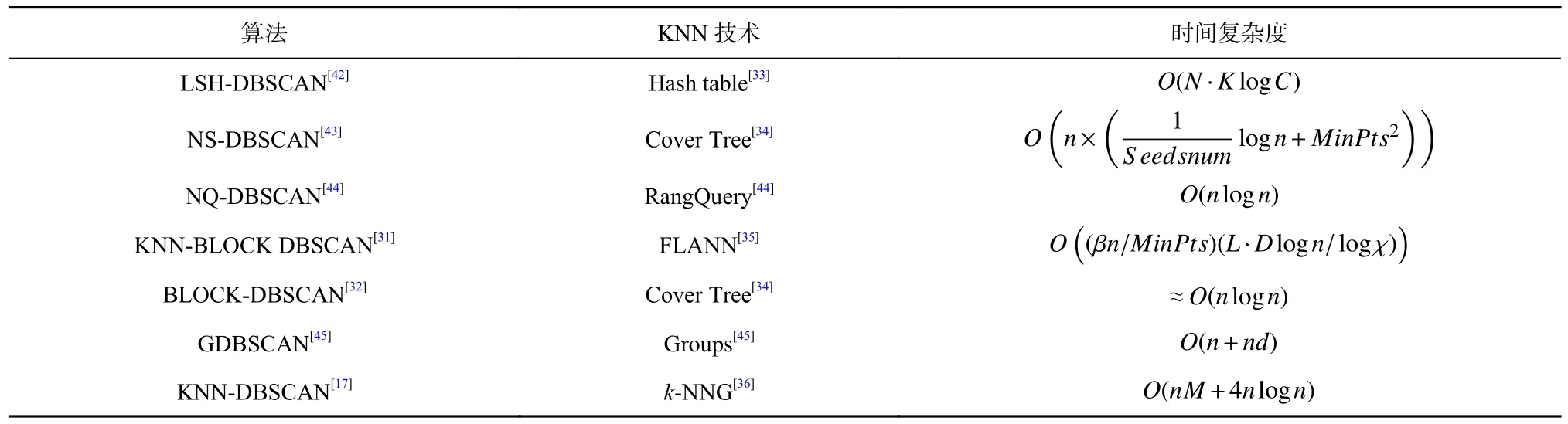
Table 3 Seven Nearest Neighbor DBSCAN Algorithms表3 7 种近邻DBSCAN 算法

此外，Chen 等人[32]提出L2和L∞版本的BLOCKDBSCAN.算法使用Cover Tree[34]来识别内部核心块、外部核心点以及边界点.该算法的时间复杂度可以控制在O（nlogn），L2版本的算法能够处理相对高维的数据，L∞版本则能够适应高维数据.

Kumar 等人[45]提出GDBSCAN（groups-DBSCAN），该算法使用分组的方法来加速搜索查询.算法主要分为2 个阶段：第1 阶段在整个数据集上运行索引结构组以获得1 组数据集；第2 阶段通过使用在第1 阶段派生的组来运行常规的DBSCAN 方法，以进行快速的ε-邻域操作.分组法将每个模式分为主模式或从模式，通过将数据拟合到一个基于图的结构来分割数据集.其中每个顶点是一个组，如果它们是可达的，则在2 组之间画一条边，然后将附近的模式不断归并到组.每一组都是一个以中心为主图案的超球体，如果一个模式不属于任何组，那么自身创建一个新的组.分组的方法确保总是为一个给定的模式进行近邻搜索，而不需要像DBSCAN 一样搜索整个数据集.与DBSCAN 相比，GDBSCAN 的时间复杂度为线性，速度提升了1.5～2.2 倍.

KNN-DBSCAN[17]算法在高低维度的数据集下都是有效的，该算法使用基于随机投影的近似算法[36]构造k-NNG，这是算法最昂贵的部分.DBSCAN 需要输入数据集的ε-NNG（ε-nearest-neighbor graph），它的内存开销达到O（n2），然而构造k-NNG 的内存开销始终保持在O（nk），这比构造ε-NNG 的内存开销要低得多.

KNN 技术主要通过加速邻域搜索操作来提升算法的效率.表3 对7 种近邻算法使用的近邻技术以及时间复杂度进行了汇总.结合表3 和图1 发现，相比于DBSCAN 算法的时间复杂度O（n2），KNN 加速技术最显著的优势在于快，算法时间复杂度近乎线性.

6 基于空间划分的加速改进

基于空间划分的加速技术是将数据空间量化为有限数目的单元，从而形成一个网格结构，并在网格上进行聚类.常见的基于空间划分的聚类算法有Grid-Clustering[46],STING（statistical information grid）[47],CLIQUE[48].相比于DBSCAN，基于空间划分的聚类可以有效地降低时间复杂度.因此，不少研究人员将空间划分的思想应用于DBSCAN 算法中，从而提升算法性能.

GriDBSCAN（grid DBSCAN）[49]使用网格来划分周围的空间，并相应地将数据点分为多个区域，每个分区分别进行DBSCAN.然后将所有分区的结果合并，从而得到数据的全局聚类.算法一开始使用d-1维的轴平行等距在超平面构造网格，如图7 所示.网格的数量留给用户选择，但粒度对算法性能有很大影响.太细的粒度会降低性能，所以网格的宽度必须在所有维度上都大于2ε.

Fig.7 Use a grid to partition space[49]图7 使用网格划分空间[49]

根据网格单元对数据分区，每个分区都由单元内的所有点（内部点）加上单元周围ε-包围的点（外部点）组成，如图8 所示.这样，外部点会被包括在多个分区，但是内部点只在一个分区，这样确保所有内部点的范围查询是准确的.考虑区分核心点和边界点，为每个分区保留一组单独的聚类标志.GriDBSCAN 通过网格的划分和网格的合并可有效地提高DBSCAN 的性能，时间复杂度为O（n2/C），其中C为网格的数量.

Fig.8 The ε range of the cell[49]图8 单元格的ε 范围[49]

Huang 等人[50]提出的GNDBSCAN 以网格为聚类单元，在网格上建立SP-Tree 索引树[51].这种方法大大提高了数据查询的效率，再利用基于密度的思想对算法进行聚类，在提高效率的同时保证了聚类精度.Gunawan 等人[52]提出了一种基于2 维网格的算法，该算法也能将时间复杂度控制在O（nlogn），但是只适用于2 维数据.

Chen 等人[53]提出了基于空间索引和网格技术的GMDBSCAN（multi-density DBSCAN cluster based on grid）算法.该算法利用空间划分技术将单个网格定义为一部分，并根据网格密度获取每个部分的局部MinPts参数，以此聚类多密度数据.再使用SPTree[51]建立索引，采用位图的邻域关系，以避免重复查询和计算.GMDBSCAN 算法中如果数据集维数不是很高，则运行时复杂度会随着数据量的增加而线性增加.

GCMDDBSCAN[54]（multi-density DBSCAN based on grid and contribution）同样也是对多密度数据进行改进的算法.在GCMDDBSCAN 中，引入空间划分、贡献值、迁移系数和树索引结构对DBSCAN 进行优化和改进.该算法显著降低了运行时间，对大型数据库的聚类能力得到了明显提高.算法的时间复杂度为O（g2），g是所有数据点网格的总数，远小于DBSCAN的O（n2），同时聚类结果的准确性没有降低.

Wang 等人[55]研究了基于空间划分和密度相结合的聚类算法，提出了GDStream（grid and density for data stream）算法.该算法将每个流数据点映射到对应的网格单元格中，利用每个数据点对邻近单元格质心的影响系数，得到网格单元格的密度，从而较好地处理了网格单元中边界点的问题.GDStream 能够快速准确地识别聚类，具有一定的可行性.

GridDBSCAN[56]利用空间信息和减少邻域查询来降低时间复杂度.GridDBSCAN 首先对数据集进行虚拟网格化，然后识别单元格的类型，如果一个单元至少包含MinPts数量的点，那么它就是一个核心单元.如果一个单元和它的直接邻域单元中存在的点的数量至少是最小的，那么这个单元就是密集的；反之，它被称为稀疏的.最后使用union-find[5]算法来合并单元格，得到全局聚类.GridDBSCAN 的时间复杂度在最坏的情况下为O（nlogn），最坏的情况是所有的单元格都是稀疏的，需要对所有的点进行邻域查询.但即使是最坏的情况，GridDBSCAN 也比DBSCAN快很多.

Sakai 等人[57]提出了一种精确版本的基于网格的DBSCAN 算法，使用最小边界矩形对连接单元步长进行高速处理，该算法可运行在高维情况下.

Boonchoo 等人[58]发现基于空间划分的DBSCAN算法存在2 个问题：相邻网格的数量随维数呈指数级增长，即邻域爆炸和合并时的冗余.为此，提出了一种名为GDCF（grid-based DBSCAN with cluster forest）的新算法.该算法利用位图索引来支持高效的邻域网格查询.其次，基于union-find[5]算法的概念，设计了一种类似森林的结构，称为聚类森林，以减少合并过程中的冗余.采用均匀随机的顺序执行合并步骤，以优化合并操作的次数.实验结果表明，GDCF算法的运行速度比传统的基于空间划分的DBSCAN算法快3 个数量级.

ρ-Approximate DBSCAN[29]采用树形索引结构，将空间通过网格划分为d维超平面，记录所有单元包含的数据点数，再使用索引结构展开聚类.该算法的时间复杂度可以控制在线性时间内.

然而，Chen 等人[31]证明了ρ-Approximate DBSCAN的线性时间仅限于非常低的维度.因此，研究人员提出KNN-BLOCK DBSCAN.该算法相对优势在于按块来处理数据，每个块都有一个动态空间范围，通过FLANN 识别核心块、非核心块以及噪声块.然后使用快速算法将彼此密度可达的核心块合并，并将非核心块中的每个点分配给适当的群集，最终得到全局聚类.图9 为KNN-BLOCK DBSCAN 的基本流程.在4～256 维数据的实验中表明，相较于ρ-Approximate DBSCAN，KNN-BLOCK DBSCAN 计算速度提高了1.5～35 倍.

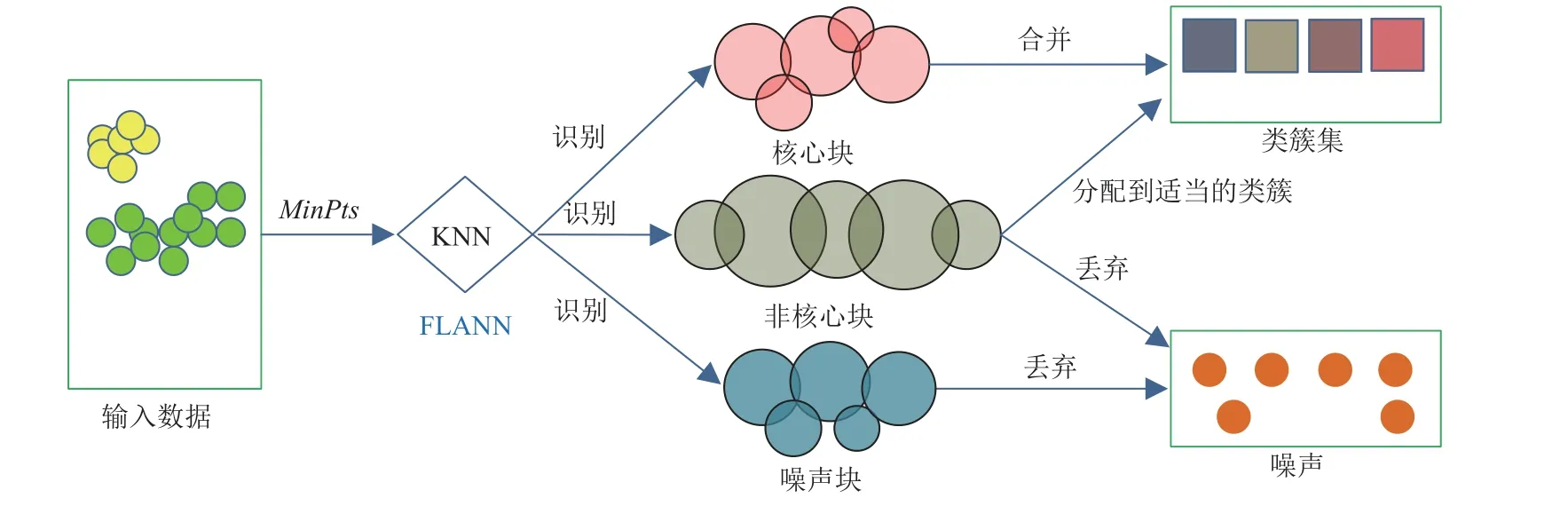
Fig.9 KNN-BLOCK DBSCAN basic process[31]图9 KNN-BLOCK DBSCAN 基本流程[31]

类似地，Chen 等人[32]还提出一个类似的算法BLOCK-DBSCAN.该算法基于近邻搜索算法Cover Tree 寻找固定大小的ε/2 范数球块，通过近似合并技术实现聚类.与ρ-Approximate DBSCAN 正好相反，BLOCK-DBSCAN 满足DBSCAN 中定义的连通性，但不满足极大性.

图10 对基于空间的DBSCAN 算法建立了关系脉络图.空间划分技术使用网格对数据空间进行划分，以网格为单元开展聚类可以有效提升速度并且能够处理多密度数据[53-54]和流数据[55].除了GDCF，空间划分技术还常与其他技术相结合，很多并行化加速算法[6-7,9-10,12-13]也使用该技术进行分区处理.

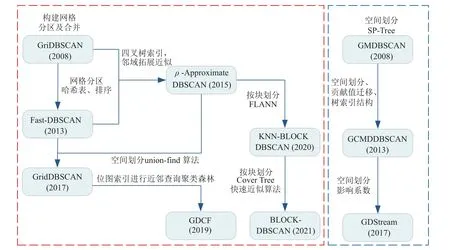
Fig.10 Relationship graph of acceleration algorithm based on space partition图10 基于空间划分的加速算法关系图

7 基于GPU 的加速改进

GPU 的主要优势是以低成本提供极高的并行性和高带宽的内存传输.研究人员也希望在聚类中能利用这些优势，因此提出了不少基于GPU 并行化的DBSCAN 改进算法.

CUDA-DClust（compute unified device architecturedensity-based clustering）[59]将对象p分配给每个线程块，并执行DBSCAN 来同时组成多个子类别.在每个块中创建的子簇称为链，通过在一个块中的多个线程同时计算不同对象与p的距离，能够非常有效地计算p的ε-邻域.如果一个对象包含在2 个或多个不同的链中会发生碰撞，碰撞链将在碰撞矩阵中进行检查.在最后阶段，所有碰撞链被合并形成一个簇.研究人员发现索引结构能够进一步提高速度，因此提出了CUDA-DClust*.CUDA-DClust 的性能比DBSCAN高15 倍，CUDA-DClust*以使用简单的索引结构将CUDA-DClust 的速度进一步提高11.9 倍.

然而，Loh 等人[60]发现CUDA-DClust 需要计算数据集中所有对象之间的距离来找到相邻对象，并且对象和计算结果存储在GPU 昂贵的片外存储器中.为此提出了一种新的算法CudaSCAN（CUDA-based DBSCAN），它通过更好地利用GPU 来提高DBSCAN的效率.CudaSCAN 由3 个阶段组成：1）将整个数据集划分为大小为GPU 中片内共享内存大小整数倍的子区域；2）并行子区域内的局部聚类；3）合并局部聚类结果.CudaSCAN 允许子区域之间的重叠，以确保每个子区域中独立、并行的局部聚类.这反过来使得对象和中间结果能够存储在片内共享存储器中，其访问成本比片外全局存储器低数百倍.CudaSCAN 的性能比CUDA-DClust 高出163.6 倍.

G-DBSCAN[61]（GPU-DBSCAN）以简单的数据索引而著称，其关键思想是使用GPU 构建与数据集相对应的密度连通图，然后对该图并行执行多个BFS（breath first search）搜索.将G-DBSCAN 与CUDA-DClust进行比较，与在CPU 上运行相比，CUDA-DClust 通过GPU 实现了15 倍加速，而G-DBSCAN 实现了112 倍加速.

Thapa 等人[62]使用了邻接矩阵法成功地实现了并行化的DBSCAN 算法.邻接矩阵法利用算法中固有的数据独立性来最大化并行性，该方法的优点是：只需要计算1 次邻接矩阵的单行，就可以确定每个点的类型.内存需求减少到O（n）数量级，可以很好地拓展到非常大的数据集中.Cal 等人[63]同样通过创建邻域矩阵将最耗时的邻域搜索和对象的数据类型信息使用GPU 并行获得，从而缩短全局计算时间.

Mustafa 等人[64]发现尽管提出了很多基于GPU 并行化的DBSCAN 加速算法，但是这些算法都没有在实验上相互比较.因此对Thapa 等人[62]的算法，CUDADClust[59]和G-DBSCAN[61]进行了实验比较，并将它们与R-Tree[8]索引的单线程也进行了比较.实验结果表明，G-DBSCAN 在所有数据集中始终是最快的，但是内存效率最低.CUDA-DClust 在速度和内存效率之间取得了良好的平衡，该算法几乎与G-DBSCAN 一样快，而消耗的内存却少了几个数量级，这使其成为较大数据集的不错选择.Thapa 等人[62]的算法，需要最少的实现工作，它可以比多线程CPU DBSCAN 算法更快，但仅适用于较大的数据集.此外，具有RTree 索引的原始单线程CPU DBSCAN 算法显示的执行时间比GPU 算法中观察到的执行时间慢几个数量级.这极大地激励了人们使用G-DBSCAN 和CUDADClust 等技术.

Mr.Scan[65]则是将基于MRNet[66]树的分布网络与配备GPU 的节点相结合，通过有效地划分点空间和优化DBSCAN 在密集数据区域上的计算来提高性能.结果表明，Mr.Scan 在17.3 min 内将推特数据集的65 亿个点聚集在Cray Titan 上的8 192 个GPU 节点上，此前所有其他并行DBSCAN 实现都只展示了聚集多达1 亿个点的能力.在此基础上，文献[67]使用消息传递而不是向文件系统写入中间文件来减少数据分发的时间，并且通过改善GPU 的负载均衡将Mr.Scan 的总运行时间缩减到8.3 min.

除此之外，还有不少算法将GPU 与其他技术相结合来提高原算法的性能.如GSCAN（grid-based DBSCAN）[68]使用网格来减少不必要的距离计算.Qian 等人[69]在传统网格的基础上提出了一种基于多网格的流数据聚类算法（multi-grid），其核心是将整个网格空间有效合理地划分为全局网格、局部网格、边界网格，从而限制了邻居的搜索范围.Chang 等人[70]提出了GPGPU-DBSCAN（GPU for graph-DBSCAN），利用相似分量的点建立索引，从而快速识别核心点.同时该算法通过与核心点的并行连接部分来指定索引操作和聚类数据的搜索条件，以减少点之间的计算量.

值得注意的是，Gowanlock 等人[71]提出的HYBRIDDBSCAN 算法将GPU 与多核CPU 结合使用，进行算法吞吐量优化，极大地降低了DBSCAN 的处理时间.这一算法使用了2 个不同的GPU 内核，再利用基于网格的索引方案来提高聚类性能.Prokopenko 等人[72]提出了一个新的GPU 上的DBSCAN 通用框架，并在框架内提出了2 种基于树的算法，分别为FDBSCAN（“fused” DBSCAN）和FDBSCAN-DenseBox.2 种算法都融合了邻域搜索来更新聚类信息，但与在处理密集区域上有所不同，FDBSCAN 关注低维数据并取得了卓越性能.

图11 对上述文献[71-72]所提的基于GPU 技术的加速DBSCAN 进行了梳理.可以发现，GPU 加速技术可以通过对数据进行划分、分配线程以及结合索引技术等显著提升算法的时间复杂度.与DBSCAN顺序处理数据相比，GPU 加速技术能够提升上百倍的速度，并且可以聚类上亿级别的大规模数据集.但对于超高维数据而言，仍然是个挑战.

Fig.11 Relationship diagram of a few GPU acceleration algorithms图11 多种GPU 加速算法关系图

8 各种加速技术比较

我们对基于不同加速技术的DBSCAN 算法所报告的最大数据量和最大维度运行时间进行了汇总，对于部分未给出数据维度信息的文章我们不作展示，如表4 所示.表5 梳理了具有聚类性能指标的加速算法，表6 对不同加速技术的优缺点进行了比较，结合图1 的多重技术使用情况，我们有5 点发现：

Table 4 Comparison of Maximum Data Amount Running Time of Typical Algorithms with Different Acceleration Techniques表4 不同加速技术典型算法最大数据量运行时间对比

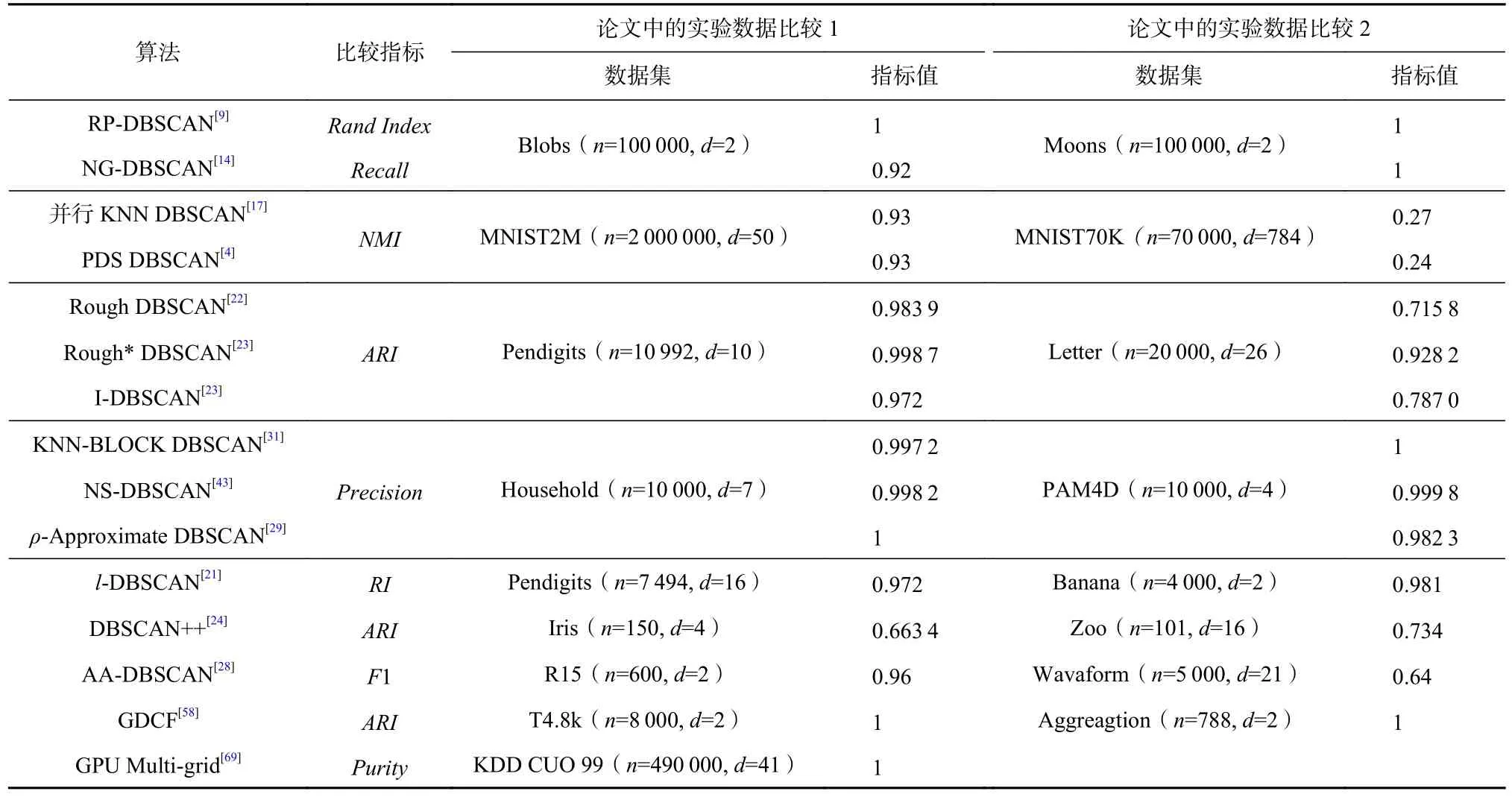
Table 5 Comparison of Clustering Performance of Different Acceleration Algorithms表5 不同加速算法聚类性能比较

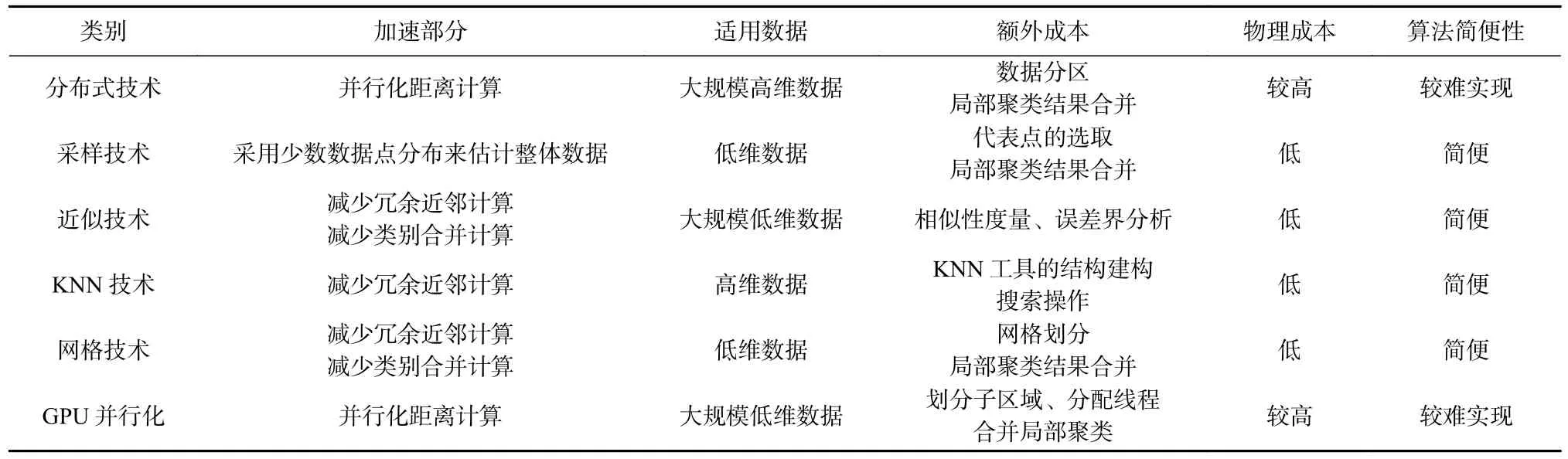
Table 6 Comparison of Advantages and Disadvantages of Different Acceleration Techniques表6 不同加速技术优缺点比较

1）从处理数据规模来看.分布式技术以及GPU并行化技术能处理的数据量最大.但分布式技术能够处理的维度相对较高且具有更高的效率.

2）从数据维度的角度来看.相对来说，基于KNN加速与近似算法处理高维数据的报告较多，但能处理的数据量还是比较有限；基于采样、基于分布式、基于GPU 的算法所能处理的数据维度也相对较高.但我们注意到伴随着维度的升高，文献中报告的数据量反而减小了，之所以有这种现象，是因为现有的这些加速算法面对大规模高维数据，还难以取得理想的效果.

3）从成本角度来看.①并行化算法成本相对较高，含有不易控制的额外成本，实现上较为困难.另外还不易移植.②对于GPU 的并行算法，主要通过CUDA 或OpenCL 完成，编程不便，不易调试，且需要针对要处理的数据特征设计出高效的数据访问与调度策略，难度较大.③KNN 技术、网格技术、采样技术以及近似模糊均致力于减少冗余计算来加速，这类算法成本低、实现容易.④近似算法损失了部分精度，但在满足一定精度的条件下，可以极大加速DBSCAN 算法.对于大规模数据而言，要准确地完成聚类成本较高，在不要求精确计算结果且成本有限的情况下，近似算法则非常适合.

4）从技术交叉角度来看.①表4 列出的高效算法中，几乎都是多种技术融合产生的.其中，并行KNN-DBSCAN 将KNN 技术与分布式结合，实现了对上百亿规模的20 维数据的数据处理，且运行极快.②空间划分技术在多数算法中都有应用，但空间划分技术在高维空间中几乎失效，因而也很难摆脱“维数灾难”的困扰.③纯粹的单一技术加速效果有限，如纯基于近邻搜索的加速算法处理的数据量不够大，纯分布式加速算法能处理的维度较低等.

5）从聚类性能来看.主要是通过聚类评价指标比较，如DI，CH，DBI，NMI，RI，ARI，F1，Purity[73-74]等.各种指标有不同的量化值来评判聚类结果的优与劣.这些指标大体上可以分为2 类.

第1 类：内部评价指标.此类指标基本上以“类内越相似越好，类别差异越大越好”为基本原则.如DI指标通过簇间分离度与簇内紧密度的比值来衡量，CH指标通过簇内紧密度和簇间分离度的比值来评价.

第2 类：外部评价指标.此类指标则是对聚类后的结果标签进行评价.如Rand Index通过判断预先定义的正确类别标签与聚类结果标签的重叠程度来进行评价，NMI通过正确的类别标签与聚类结果标签的互信息进行评价.然而，实际上很少有这样的经过人工标注过的大规模数据集.因而，有些算法将原始DBSCAN 的聚类结果作为“标准答案”，在使用相同参数的前提下与之对比，应用匈牙利算法[75]计算出准确度，如KNN-BLOCK DBSCAN 和BLOCK DBSCAN[31-32].但是，这种比较也只能仅在小数据集上，其原因在于原始DBSCAN 时间复杂度过高，难以在大规模数据集上运行.

目前，表4 中所列的算法主要工作都是在比较速度，而性能比较的报告较少.另外，有多数算法未提供代码，提供源码的也有一部分因各种原因不能运行，如LSH-DBSCAN[42]缺少相关运行库.所以，表5显示了部分性能比较.

从表6 可以看出，不同的加速技术所采用的聚类评价指标有所不同，如近似技术通过与DBSCAN 结果的相似程度来判断聚类效果的好坏，采样技术则通过不同类别的相同结果进行评价.但是，这些加速算法都能获得与DBSCAN 相当的聚类效果.

9 快速DBSCAN 在多个领域的应用

DBSCAN 自1996 年被提出以来，至今已有近30 年.该算法广泛应用于各个领域，如数据挖掘、图像处理、生物农业及其他应用[76-81].快速化DBSCAN在异常检测、数据挖掘、图像处理、生物医学、网络安全等众多领域也有不少应用.下文将对3 个主要的应用领域进行介绍.

9.1 异常检测应用

称重设备是散装物料贸易的测量设备，由于长时间高负荷运行，计量不准确等故障频繁发生，直接造成了大量的经济损失.因此，及时检测、诊断是很有必要的.电子皮带秤是使用最多的称重设备，Zhu等人[82]以皮带秤作为研究对象，对其进行故障检测和诊断.为了实现皮带秤的智能检测和诊断，提出了一种方案，即提取正常数据的同时利用聚类算法检测故障数据，然后通过对检测到的故障数据进行分类来识别故障模式.所使用的聚类算法是利用相似性函数代替距离函数的改进DBSCAN，并将其应用于沸水在线故障检测，以应对不同物料流量或同一流量的物料在任意称重单元上随时增减而导致的密度数据不均匀.使用改进的DBSCAN 的皮带秤故障检测模型具有良好的实时性和对处理不均匀密度数据的鲁棒性.

Chernov 等人[83]为聚类技术在工业和运输中的应用提供了一个新的领域，提出了铁路智能控制系统网络子系统产生的电信业务点异常检测技术，使用PDBSCAN[3]在IP 网络数据中进行点异常检测.考察了中国铁路运输协会售票服务的交通流量，这部分铁路运输信息系统是实时运行的，但它处理的运输量并不像主要铁路运输过程中所涉及的子系统那样庞大.PDBSCAN 技术能够适用于铁路智能控制系统网络基础设施中由各种事件引起的点异常的鲁棒检测.

Ghallab 等人[84]在DBSCAN 的基础上，利用弹性分布数据集来检测影响物联网技术数据质量的离群点，在提高检测质量的同时还能够处理高维数据.Garg 等人[85]则是提出了一种新的多阶段异常检测技术支持在物联网的应用上执行计算.在提出的解决方案的第1 阶段，从数据集当中捕获相关的特征集，第2 阶段将特征集进行分割，第3 阶段采用LSH[33]来解决最近邻搜索问题，最后得到参数集对异常数据进行检测.

9.2 数据挖掘应用

Web 用户挖掘是挖掘技术在Web 日志数据库中的应用，它用于从Web 访问日志中查找用户访问模式.Santhisree 等人[86]提出了一种新的粗糙集DBSCAN聚类算法，用于识别用户页面访问的行为、访问发生的顺序，使得在发现共同兴趣的群体上具有更好的效率.

Yu 等人[87]则是通过分区的DBSCAN 高效地从日志数据中聚类大量的网络文档.改进的DBSCAN除了能在网络日志中挖掘出有用信息，在地震监测中也有应用.Scitovski[88]考虑将Rough-DBSCAN[22]应用于地震区域划分.使用Rough-DBSCAN 不仅能对地震进行分区，识别出非凸形状，而且能降低时间复杂度，进一步用于大型数据集.

在高分辨率雷达系统中，采样密度往往是非等距的，使用普通的聚类算法往往不能达到想要的效果.为此，Kellner 等人[89]提出了基于网络的DBSCAN来处理高分辨率雷达数据，在保持原有算法优势的同时，对杂波和非等距采样密度具有鲁棒性且在速度上优于原始算法40%～70%.

Xia 等人[90]发现复杂的城市交通网络为移动乘客推荐出租车等候点时有困难，且在Spark 并行处理框架下，DBSCAN 的边界识别尤为困难.因此，提出了优化后的SP-DBSCAN 算法，该算法不仅解决了传统DBSCAN 的数敏感问题，能够为客户推荐最佳的候车点，而且在分布式框架上解决了大规模流量数据的数据分区和聚类时的分布式存储和并行计算问题.

9.3 图像处理应用

聚类算法在图像处理中也有不少应用，Bandyopadhyay[91]将k-means[2]聚类和DBSCAN 应用于人脑核磁共振图像中脑肿瘤的聚类和分割问题.使用了大量来自放射影像数据库的核磁共振影像进行实验，发现k-means 的聚类结果比较嘈杂，但是许多聚类还能进一步分析.而DBSCAN 由于输入数据密度高度集中，聚类效果让人满意.

Baselice 等人[92]对于核磁共振图像提出了一种新的分割方法，其基于2 个主要的创新：1）该方法利用每个像素的估计质子密度和弛豫时间，而不是其灰度强度，该特征使得该算法特别健壮，并且允许对识别的片段进行分类.2）该方法使用了GDBSCAN[93]方法在区域估计的有效性方面获得了优势，与基于欧几里德距离的技术相比，该技术能够提高正确的分类率.

Kurumalla 等人[94]提出了一个高效的DBSCAN算法用于图像分割，该方法使用了KNN 和DBSCAN技术来确定所需要的 ε和最小点数.首先将RGB 彩色图像转换为灰度图像，然后使用图像处理的滤波技术从转换的图像中去除噪声，从而确定参数值，即最小点数和ε值.将这些参数作为初始值，对与ε和最小点数相关的灰度图像执行原始的DBSCAN 聚类算法.与现有的图像分割方法相比，该方法大大降低了图像中的噪声，分割效果也有所提高.

10 总结与展望

DBSCAN 是基于密度聚类算法中最为常见的算法之一，其算法由于思想简单、能够识别不同形状的簇且有效地处理噪声点而倍受欢迎，但是算法时间复杂度高达O（n2）以至于无法处理大型数据集.因而许多研究人员进行了深入而有成效的工作，极大地提升了DBSCAN 的速度.

本文梳理了前人对于提升DBSCAN 速度的研究，从加速手段所针对的目标角度看，可以分为减少冗余计算和并行化两大类.但从具体的加速手段来看，本文按3 个规则提出了一个简单的划分方法，并将这些方法分为6 个类别：基于分布式、基于采样技术、基于近似模糊、基于快速近邻、基于空间划分技术、基于GPU 加速技术.

我们发现，多技术融合的加速算法（特别是分布式、近似近邻搜索技术）要远优于其他单技术加速算法，其中近似模糊化、并行化与分布式化是当前最为行之有效的方法，但成本较高、不易实现.

虽然这些改进在一定程度上都可以提升算法速度，但是还有一些局限性，还存在一些挑战，即未来可以研究的方向：

1）利用单种或少数几种技术对 DBSCAN 进行加速效果还稍显不足.近年在近邻搜索与GPU 并行化加速工作上有不少进展，如FAISS[98]利用GPU 可实现数十亿级别数据的快速精确/模糊KNN 检索.通过类似FAISS 与其他技术融合来改进DBSCAN 的工作还鲜有报道.

2）当数据大规模地分布在众多相互不能共享的环境中时（如众多医疗数据分散在各个不同医疗机构，相互之间因竞争关系不愿或不能相互共享）[95-96]，针对这类涉及到隐私的数据，现有的DBSCAN 也无法完成聚类.

3）绝大多数现有的算法将数据一次性读取，然而当数据达到TB 级别规模时，现有的算法仍然很难处理.另外，对于大规模的不均衡数据[97]，平衡好并行任务之间的负载有待深入研究[4,6-7].

作者贡献声明：陈叶旺提出了研究命题，设计了研究思路，负责论文的撰写；曹海露负责论文的补充和修改；陈谊负责论文整体结构；康昭、雷震负责审核与修订其中部分算法；杜吉祥负责最终版本修订.