例谈高中Python教学中计算思维培养的策略
高连 浙江省湖州中学
●高中Python教学中计算思维培养存在的问题
在信息技术课堂中充分挖掘教学资源,培养与发展学生的计算思维仍困难重重,充满挑战。具体表现在以下三个方面。
1.计算思维概念理解不透彻
计算思维是运用计算机科学的基础概念进行问题求解、系统设计,以及人类行为理解等涵盖计算机科学之广度的一系列思维活动,然而很多教师常是机械化地完成每节课的操作任务,不能将计算思维很好地融入项目教学,无法有效传达计算思维的核心概念。
2.“解构”与“模式识别”不充分
在实际生活中,大部分学生对具体问题不会解构,而部分教师没意识到这个问题,导致在教学中遇到需要结构的问题时,没有引导学生如何思考、解构和模式识别。
3.总结、归纳不到位
在教学中,教师常采用题海战术,很少深入分析题目间的差异,并总结归纳题目之间的联系,导致学生花费大量时间做题,但无法有效提升解决问题的能力。
●高中Python教学中计算思维培养的策略
1.体验使用“计算思维”解决问题的过程
高中信息技术课程要求学生通过具体的技术操作体验,理解其背后的原理与格局、特点与局限,拓宽视野,发展思维。因此,教师可将学生的学习问题进行整合,帮助学生分析问题,并引导学生自主解决问题,培养其计算思维。
下面,笔者以编写计算机程序(Python turtle)绘制一个正方形为例,呈现引导学生使用计算思维解决问题的步骤。
正方形是四边形,相邻的两个夹角是90度,首先向Python turtle发出指令,让它画出一个正方形,调整函数的参数可以绘制不同大小的正方形。教师要引导学生做好问题的解构,使其了解更细致的内容,进而明确实际操作的步骤,即使用forward(distance)指令让小乌龟前进一个指定的距离,使用turtle.left(degree)指令让小乌龟逆时针转动90度,如下页图1所示。接着,教师引导学生可以将该问题的计算思维“灌输”给小海龟,让它根据自己的思维执行相应的动作。

图1
通过“解构”,把一个复杂问题分解成了一系列可控而容易解决的简单任务,这样能让学生明白接下来的操作步骤。具体指令如图2所示,运行结果如图3所示。

图2
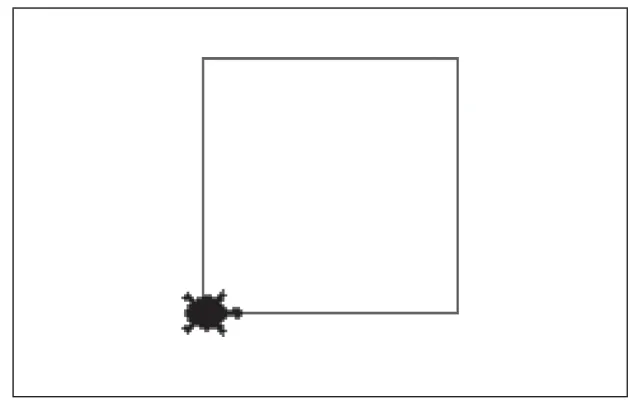
图3
学生通过观察发现,绘制一个正方形,相同的指令重复了4次,使用了8行代码。若要绘制一个正六边形,则相同的指令需要重复6次,使用12行代码,只不过是转动的角度不同。基于此发现,学生便可以设计算法,解决类似的问题。
接下来,就可以引导学生利用for循环编制程序,具体如图4所示。

图4
引导学生进一步思考,他们会发现只需要进行两处修改便可以实现代码重用,可以推广到任意正多边形(如图5),运行结果如图6所示。

图5
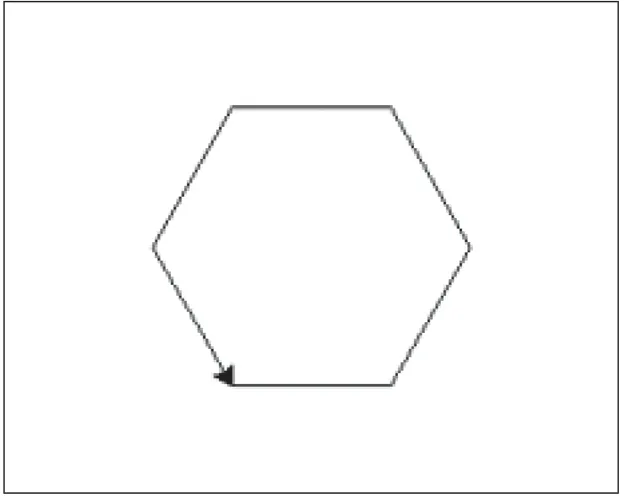
图6
turtle绘图是一个十分有趣的算法学习方式,教师引导学生独立进行实践操作,强化了学生的计算思维,激发了学生的积极性,也使学生在计算思维的体验中明白了知识间的关联性。
2.使用算法解决数学问题,培养计算思维
具备计算思维的学生,能对问题进行抽象、分解、建模,通过设计算法形成解决方案,并将其迁移运用于解决其他问题。下面是引导学生使用算法解决数学问题的例子—欧拉计划的问题(Project Euler)。
网格路径:从一个2×2网格的左上角出发,若只允许向右或向下移动,则恰好有6条抵达右下角的路径(如图7)。那么,对于20×20网格,这样的路径有多少条?

图7
利用计算思维的解构与模式识别,会发现以下的规律:
这个网格是一个带有四个小方格的正方形。想要找到所有路径,可以选择从左上角出发,则最上面一条边的点只能是从左面过来,最左面一条边的点只能是上面点过来,所以它们都只有一种路径,而中间的点既可以是上面点过来,又可以是左面点过来。
进一步抽象之后,得到状态方程:dp[i][j]=dp[i-1][j]+dp[i][j-1]
具体的Python程序如图8所示。

图8
3.借用多层需求与多位格局案例发展计算思维
案例:智能城市交通优化。
背景:某城市的交通问题越来越严重,交通拥堵和交通事故频发。为了解决这个问题,政府决定引入计算思维来优化交通系统。
多层需求:
市民需求—市民希望能够更快、更安全地出行,减少交通拥堵和事故风险。
环境需求—减少车辆拥堵,降低尾气排放,改善空气质量,减少噪音污染。
经济需求—提高交通效率,减少时间浪费,促进经济发展。
多位格局:
政府部门—负责制订交通规划和政策,管理交通系统运行。
车辆驾驶员—负责遵守交通规则、道路安全,确保自身行车安全。
交通管理机构—负责交通信号灯、路牌等设施的设置和维护。
解决方案:
数据收集与分析—通过城市摄像头、交通传感器等设备收集交通数据,包括车流量、拥堵情况、事故发生地点等。
算法优化与模拟—使用计算机模拟来预测交通流动情况,根据实时数据和历史数据,进行路网优化、信号灯优化等。
交通管理与协调—基于优化的结果,交通管理机构可以及时调整信号灯时间、道路限行政策等,以减少交通拥堵。
数据共享与智能导航—将优化后的交通数据共享给市民,让他们可以通过APP等方式获取实时路况信息,选择最佳路径出行。
教师利用案例引导学生利用计算思维来解决城市交通问题,启发了学生思考问题及解决问题的方式。同时,还应为学生提供相似的例题展开专题练习,巩固计算思维的培养。
根据教学实践,笔者认为例题可从以下三种来源中选取:
一是选考真题中的主观题。题目综合性强,涉及多维度的复杂问题,教师可以根据其提供的情境,进行适度的改编。
二是信息学竞赛中的相关试题。题目可能晦涩难懂,教师可通过讲解,激发学生找到化繁为简、深入浅出的表述方法,并最终达到触类旁通、举一反三的学习目标。
三是各类联考卷中的“大题”。教师可以收集并选择合适的题目,进一步抽象、提炼、整合。
总之,教师要积极培养学生的计算思维,使其能够对现实中的真实问题提出新的解决方案,创造性地解决问题。

