哈密尔顿图的一些充分条件

许秋晨，叶淼林

（安庆师范大学 数理学院，安徽 安庆 246133）

设G=G(V,E)为n阶简单连通图，其顶点集V=V(G)={v1,v2,…,vn} ，边集E=E(G)为V的二元重集构成的集合，称E中元素{u,v} (u≠v)为G的边，边{u,v} 简记为uv。顶点ν的度dG(ν)是指G中与v关联的边数，G的最小度记作δ。Kn是n阶的完全图，Km,n为完全二部图。设G1=G(V1,E1)与G2=G(V2,E2)是两个不交的简单图，它们的并图为G1⋃G2=(V1⋃V2,E1⋃E2)，又记为G1+G2；如果G1=G2=…=Gk，用kG1来表示G1⋃G2⋃…⋃Gk；G1和G2的联图为G1∨G2，即在G1⋃G2中添加G1中每个顶点到G2中每个顶点的边所得到的图。

图G的邻接矩阵为A(G)=[aij]n×n，当vi,vj相邻时，aij=1，否则aij=0 ，i,j=1,2,…,n，我们称A(G) 的最大特征值为图G的谱半径，用ρ(G) 来表示，简记为ρ。设D(G)=diag(d(v1),d(v2),…,d(vn)) 是图G的度对角矩阵，定义图G的无符号拉普拉斯矩阵Q(G)=D(G)+A(G) ，Q(G) 的最大特征值被称为图G的无符号拉普拉斯谱半径，记作q(G)，简记为q。

通过G中所有顶点的圈叫哈密尔顿圈，含有一个哈密尔顿圈的图叫做哈密尔顿图。图的哈密尔顿问题一直是图论中的经典问题，但是迄今为止，图的哈密尔顿问题依旧NP-完全问题，还没有被完美的解决，还有很多问题值得被研究。目前，已经有许多学者从边条件、谱半径以及无符号拉普拉斯谱半径出发，对图的哈密尔顿性进行了研究，也得出了一些结论。如周倩楠等人[1]借助边的大小给出了图是哈密尔顿的充分条件，后又[2]通过谱半径以及无符号拉普拉斯谱半径给出了哈密尔顿图的一些充分条件；徐奕等人[3]从图的大小，谱半径以及无符号拉普拉斯谱半径出发，给出了图是哈密尔顿-连通的一些充分条件；余桂东等人[4]研究了具有较大最小度的平衡二部图的可迹条件和哈密尔顿的谱充分条件。受周倩楠等人理论的启发，本文主要改进图的边数条件，提出了哈密尔顿图的边充分条件，并在此基础上给出了哈密尔顿图的谱充分条件。

1 预备知识

引理1[1]设G是阶数大于6，边数为m的简单图，且δ（G）≥6，若，则G包含哈密尔顿圈，除非G∈NC。

引理2[5-6]设G是一个连通图，如果H是G的子图，则ρ(H)≤ρ(G)，q(H)≤q(G)，当且仅当H是G的真子图时不等式严格成立。

引理3[7]设G是阶数大于4 的图，且度序列为(d1,d2,…,dn)，如果不存在一个整数，使得dk≤k，dn-k≤n-k-1，则G是哈密尔顿图。

引理4[8]设G是有n个顶点m条边的连通图，则有，当且仅当G=Kn或G=K1,n-1时等号成立。

引理5[9]设G是有n个顶点m条边的简单图，则，如果G是连通图，当且仅当G=Kn或G=K1,n-1时等号成立；如果G不是连通图，当且仅当G=Kn-1+v时等号成立。

2 主要结果

定理1 设G是阶数大于6，边数为m的简单图，且δ（G）≥6，若，则G是哈密尔顿图，除非G∈NC⋃NP。

由引理1可知，G是哈密尔顿图，除非G∈NC。

假设G不是哈密尔顿图，设G的度序列为(d1,d2,…,dn)，且d1≤d2≤…≤dn，di=d(vi)，i∈{1 ,2,…,n}。

由定理条件得

因此(k-3) (2n-3k-10)≤2，因此接下来将分成四种情况来进行讨论。

情形2.1 (k-3)(2n-3k-10)=2

在这种情形下，有k-3=2 且2n-3k-10=1或k-3=1 且2n-3k-10=2，我们可以得到k=5，n=13 或k=4，n=12，均与k≥6 矛盾，所以此种情形排除。

情形2.2 (k-3)(2n-3k-10)=1

在这种情形下，有k-3=1 且2n-3k-10=1，此时我们找不到满足条件的k和n。

情形2.3 (k-3)(2n-3k-10)=0

在这种情形下，有k-3=0 或2n-3k-10=0，而k-3=0，即k=3，与k≥6 矛盾，所以此种情形排除，因此，只有 2n-3k-10=0 ，即，我们可得n≤19。

通过计算，我们可得k=6 ，n=14 或k=8 ，n=17。

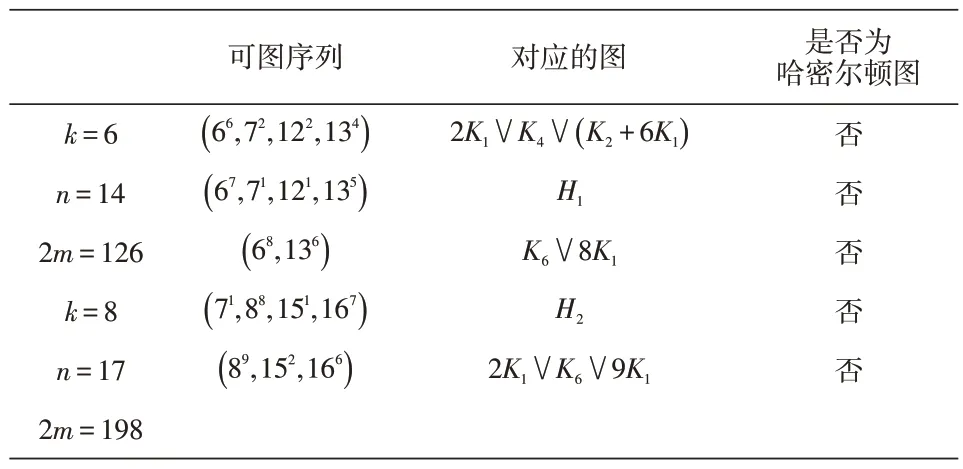
表1 情形2.3中可图序列及其所对应的图

情形2.4 (k-3)(2n-3k-10)＜0

因为k≥6 ，所以 2n-3k-10 ＜0 ，即，又因为，因此我们可得13 ≤n≤19。

情形2.4.1n=19

与2n-3k-10 ＜0 矛盾，所以此种情形排除。

情形2.4.2n=18

情形2.4.3n=17

情形2.4.4n=16

情形2.4.5n=15

当k≤6 时，2n-3k-10=20-3k＞0 ，与2n-3k-10 ＜0 矛盾，所以此种情形排除。

当k=7 时，2n-3k-10=-1 ＜0，此时d7≤7，。所有可图的度序列及其对应图如表2所示。

表2 情形2.4.5中可图序列及其所对应的图

情形2.4.6n=14

情形2.4.7n=13

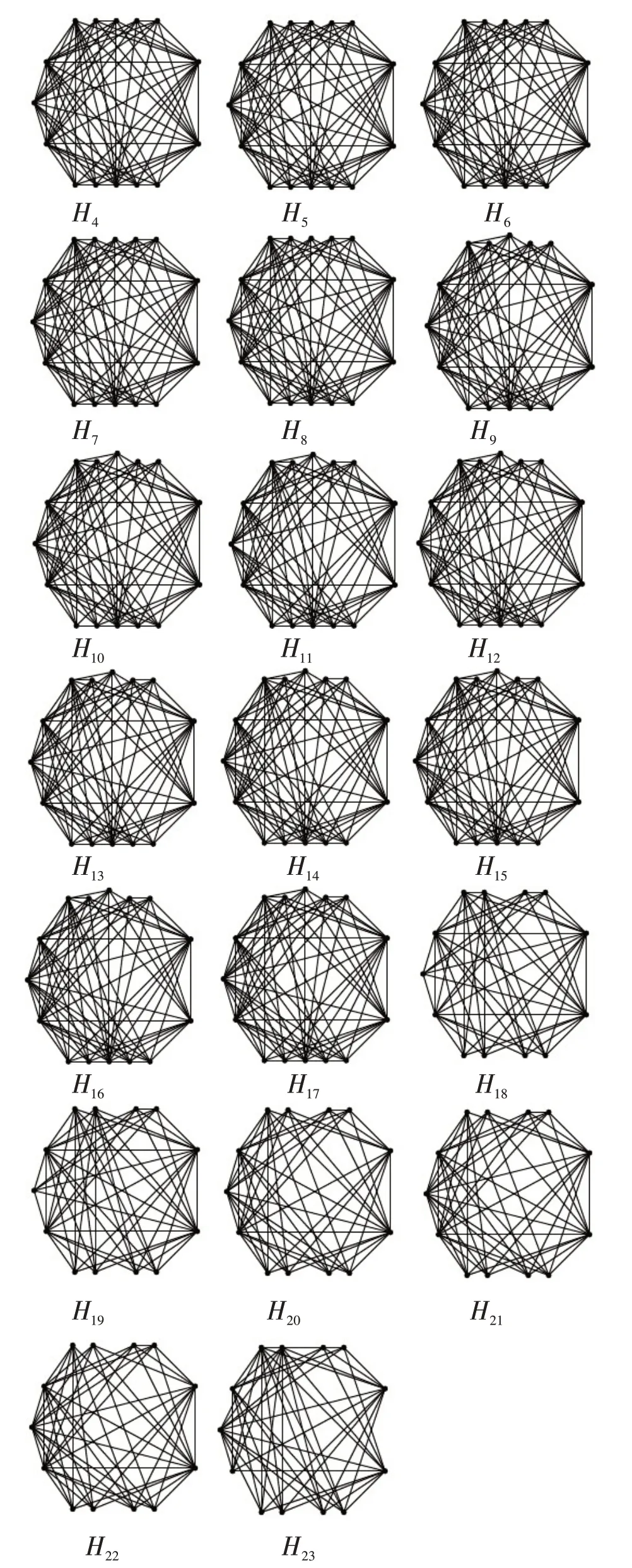
图1 H1 ～H23

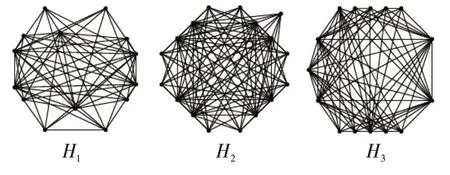
表3 情形2.4.7中可图序列及其所对应的图

定理2 设G是阶数大于6，边数为m的连通图，且δ（G）≥6，如果，则G是哈密尔顿图。

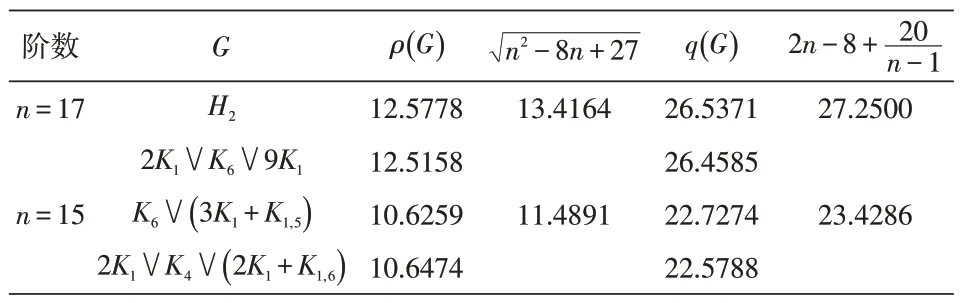
表4 图的谱半径和无符号拉普拉斯谱半径

H9 n=14 H10 H1 10.5357 21.5385 K6 ∨8K1 2K1 ∨K4 ∨()n=13 K2+6K1 K1，2 ∨K3,7 9.5917 19.6667 H23 10.6658 10.7190 9.8208 9.8655 9.7499 8.6023 8.6451 22.6723 22.7941 21.0142 21.1652 20.7743 18.0702 18.2818

定理3 设G是阶数大于6，边数为m的连通图，且δ（G）≥6，如果，则G是哈密尔顿图，除非G=K6∨7K1。

3 结语

本文从边条件、谱半径以及拉普拉斯谱半径出发，来探讨图的哈密尔顿性，并结合相关引理进行了分类讨论，找到了判定图的哈密尔顿性的改进充分条件，丰富了图的性质研究。