基于改进烟花算法的农产品运输调度研究

李佳晖，代永强

（甘肃农业大学 信息科学技术学院，兰州 730000）

0 引言

近年来，随着电子商务经济以及交通体系的发展，我国物流正向着高速、高效、稳定的方向发展。但目前物流运输还存在调度不合理的问题，这对我国物流保障的能力和速度都会造成不良影响，因此合理安排物流运输中的调度问题尤为重要。烟花算法（Firework algorithm，FWA）[1]是一种群智能寻优算法，由谭营教授等人于2010 年提出，目前已广泛应用于不同领域，并且取得了一系列成果。但基本烟花算法也存在很多问题，比如容易陷入局部最优、求解效率低下、多样性较差等问题。

目前烟花算法已经有了一些改进方法。一方面，对烟花算法本身的因子进行改进，如郑少秋等人[2]提出了增强型烟花算法（Enhanced fireworks algorithm，EFWA），针对爆炸算子改进，引入了最小爆炸半径，以增加种群多样性，但未考虑适应度值对选择策略的影响；Pei 等人[3]提出了加速型烟花算法（Accelerated fireworks algorithm，AcFWA），将最优位置作为启发式信息引入到当前种群进行加速搜索，提高了求解效率；Li 等[4]提出了骨架烟花算法，该算法计算简单、参数少、求解效率高；ZHAO 等[5]通过改进最优烟花因子，提出一种引导自适应烟花算法，有效提高了全局搜索能力；包晓晓等[6]改进了烟花算法，使用了最大位置法来解决置换流水车间问题，具有很好的求解精度和鲁棒性。另一方面，将基本的烟花算法同其他的智能优化算法相结合，如郭京蕾等[7]提出一种基于差分变异算子的烟花算法，提高了烟花种群多样性，增强了算法精度；张玮等[8]结合烟花算法和蚁群算法，提出了一种混合烟花算法，有效解决了智能移动体避障问题；GAO 等[9]提出的文化烟花算法（Cultural firework algo-rithm，CA-FWA）成功应用于数字滤波器设计的计算；Zhang 等[10]将生物地理学优化方法（Biogeographic optimization，BBO）加入到增强烟花算法中，形成生物地理学优化-烟花混合算法（Biogeography optimization fireworks algorithm，BBO-FWA），很好地改善了种群多样性，提高了个体之间的信息交流。

针对大规模复杂优化问题，目前基本采用智能算法求解，如粒子群算法（Particle Swarm Optimization，PSO）[11]、蚁群算法（Ant Colony Optimization，ACO）[12]、遗传算法（Genetic Algorithm，GA）[13]等。然而蚁群算法搜索时间长，初始种群对其影响较大；粒子群算法容易陷入局部最优；遗传算法处理较复杂的问题会耗费大量时间；烟花算法在离散问题上有很好的求解能力。曹磊[14]提出了用烟花算法解决车间调度问题；ALI H 等[15]提出了用离散烟花算法解决物联网网络选址问题；LI J Z等[16]提出一种新的爆炸火花分布方式和淘汰锦标赛策略，该算法在解决多模式优化问题上具有较好的效果；CHENG J 等人[17]提出将多目标返工算法与重新调度烟花算法相结合，提高了算法的稳定性，但增加了算法复杂度；DING 等[18]在FWA 的基础上提出了基于GPU 平台的并行烟花算法。不过目前烟花算法在农产品物流运输调度问题上的研究还比较少。本文提出一种混沌烟花算法（Chaotic Fireworks Algorithm，CFWA），利用混沌序列产生爆炸半径的方法，增强种群多样性，加强全局搜索能力，因而该算法具有更高的搜索效率，能在短时间内找到最优的调度方案。

1 农产品物流调度问题建模

农产品物流运输调度模型可以描述为：一个农产品库和多个客户点的供应链中，该农产品库点可用一定数量的车把货物分配给多个客户点，每个客户点必须配送且只能配送一次，确保所有农产品库的车辆能够满足客户点的货物需求。目标是最大限度地满足车辆载重和配送距离等要求，在规定时间内，使物流运输成本降到最低。

考虑到数学计算的方便性以及仿真实验的可行性，模型采取如下假设：农产品库存充足，可以满足全局的供给要求；车辆由一个配送中心出发，服务完客户后须返回出发点；如果车辆不能在规定时间内完成对客户点的服务，则产生等待成本或进行适应度惩罚；每辆车的载重量相同；每辆车的运载能力都是有限的，所以在农产品物流运输中不允许车辆超载。例如，有A 个农产品库点和B个客户点，农产品库点a的车辆载重量（q）相同，车辆数量为La（a=1，…A），客户点n的农产品需求为Gi（i=1，…B），每个客户点的服务时间为Si，且只能有一辆车在允许时间内Hi（i=1，2，3…B）进行服务，农产品运输车辆在客户n到客户j的时间以t（n，j）表示，也可表示为tnj。

在农产品物流运输调度中，都会产生成本。比如油耗、汽车行驶距离、司机的薪酬等。在实际运输中，也不可能有无限多的车辆，因此要保证所有农产品库的车辆满足所有客户的需求，就要对每个农产品库的车辆进行统计。设客户点的编号为（1，2，3…B），则货场的编号是（A+1，A+2，A+3…A+B）。根据以上描述和条件约束，总结出农产品物流运输数学模型：。该模型中l为农产品库点车辆的编号∈（L1，L2，L3…LA），公式意为a点的第l辆车从客户n点行驶到j点。

一辆车运输农产品的成本是由司机的底薪和单位时薪和行驶时间构成的，因此公式可以写为：

costal为a货场中第l辆车运输的总成本，ba为该辆车司机的底薪，Ta为单位时间内司机的薪酬，tl为该辆车运输的时间。

其他约束性条件为：

其中，式（1）为农产品库a点的第L辆车单次运输成本；式（2）的目标函数为最小化调度总成本，第一项为所有车辆的行驶时间求和，第二项为每个客户点的最大服务时间，第三项为所有车辆的行驶成本；式（3）为每个农产品库点出发的车辆数不能超过自身总共的车辆数；式（4）表示车辆从农产品库点出发完成配送后必须返回原农产品库点；式（5）表示每个客户需求地仅被一辆车服务一次；式（6）表示车辆不能从客户点n到达客户点j；式（7）为车辆服务路径上的需求数小于车辆自身的负载数；式（8）表示如果车辆从n客户点到j客户点，则j点到达时间要等于n点开始时间加服务时间加行驶时间。

2 混沌因子烟花算法

2.1 烟花算法

烟花算法是谭营教授等人2010 年提出的新型智能算法。算法主要包括爆炸算子、变异算子、映射规则和选择策略四部分。研究表明，烟花算法在解决不同类型优化问题时有较好的求解能力。

2.1.1 爆炸算子

烟花种群N 中爆炸幅度R_i的计算公式为：

其中，Ri为第i个烟花的爆炸半径，R 为常数，f（i）是第i个烟花个体的适应度值，加入常数ε 是为了避免除零情况。

烟花爆炸火花数计算公式为：

其中，Si是第i个烟花产生的火花数量，S 为常数，f（i）是第i个烟花个体的适应度值，加入常数ε 是为了避免除零情况。

为了控制烟花的数量，以产生更好的烟花，对烟花个数做如下限制：

火花数量Si小于round（a×S），大于round（b×S），其中a 和b 是常数，取值范围为［0，1］，round是取整函数。

2.1.2 变异算子

对于高斯变异操作，产生M个高斯火花数，公式如下：

其中，烟花&xki表示经过高斯变异后的烟花，表示烟花xi在维度k上进行变异，c～N（1，1），N（1，1）表示均值为1、方差为1 的高斯分布。

2.1.3 映射规则

爆炸之后，还需要对烟花的上下界范围进行保证，把不在范围内的烟花重新映射其中，计算公式如下：

2.1.4 选择策略

为使烟花种群中优秀个体传递到下一代，对于种群N，适应度最小的个体直接保留到下一代，剩余的N-1 个体应用轮盘赌方法计算选择概率，计算公式如下：

其中，∑i∈kd（xi-xj）是种群中当前个体xi与除xj之外的所有粒子的距离之和，Pxi为选择下一代个体的概率。

2.2 改进的烟花算法

由于原始的烟花算法中，爆炸和变异对粒子整体变换，所以在迭代过程中会丢失很多可行解信息，导致算法易陷入局部最优、运行速度慢等问题。针对农产品物流调度这一问题模型，基本烟花算法爆炸范围大，易产生不相关搜索，为解决这一问题，本文对基本的烟花算法（Firework algorithm，FWA）进行改进，提出一种混沌烟花算法（Chaotic Fireworks Algorithm，CFWA），利用混沌方法产生爆炸半径，提高全局搜索能力，引入精英选择策略，加快算法收敛速度。

2.2.1 对爆炸算子的改进

因为适应度较小的烟花会在较小范围内产生更多烟花，影响种群多样性，易陷入局部最优。混沌是一种由简单的确定性系统产生的随机性序列，对烟花算法来说，有利于避免算法陷入局部最优值[19]，增加种群多样性。混沌映射有多种映射规则，Logistic 映射是其中的一种，它的特点是概率密度图像呈U 型分布，具有很好的遍历性和随机性，所以本文采用Logistic 混沌映射。它的表达式为：

式中，只有当3.569 945 6＜u≤4 时，Logistic 混沌映射才具有混沌状态，xn是混沌域，取值范围为（0，1）。在烟花爆炸过程中，采用Logistic 混沌方法，可以有效避免适应度较小的烟花在较小范围内产生更多烟花。采用Logistic 混沌方法产生爆炸半径，公式如下：

式中，Ai+1为下一代的半径，Ai为当代粒子的半径，u是常数，R 也是常数。

2.2.2 对选择策略的改进

基本烟花算法采用基于欧氏距离的选择策略，通过计算欧式距离占比概率高低选择下一代烟花，这种策略计算量大、求解效率低、算法性能一般。所以本文采用一种精英—随机选择策略[20]，这种选择策略计算量小、简单、求解效率高，具体操作过程如下：首先，将当代候选集M 里适应度最小的粒子，也就是最优的粒子作为下一代；然后，候选集M 中剩余的个体随机选择进入下一代。

这样的计算策略不仅可以大大降低计算复杂度，减少计算时间，而且加快了收敛速度和算法求解速度，提升了适应度较差的个体被选择的概率，增加了种群的多样性。

2.3 算法的基准测试函数图对比

为验证混沌烟花算法（CFWA）的有效性，进一步验证算法的收敛速度，采用基本烟花算法（FWA）、粒子群算法（PSO）、混沌烟花算法（CFWA）3 个算法对4 个测试函数进行仿真实验，实验结果如图1 所示。

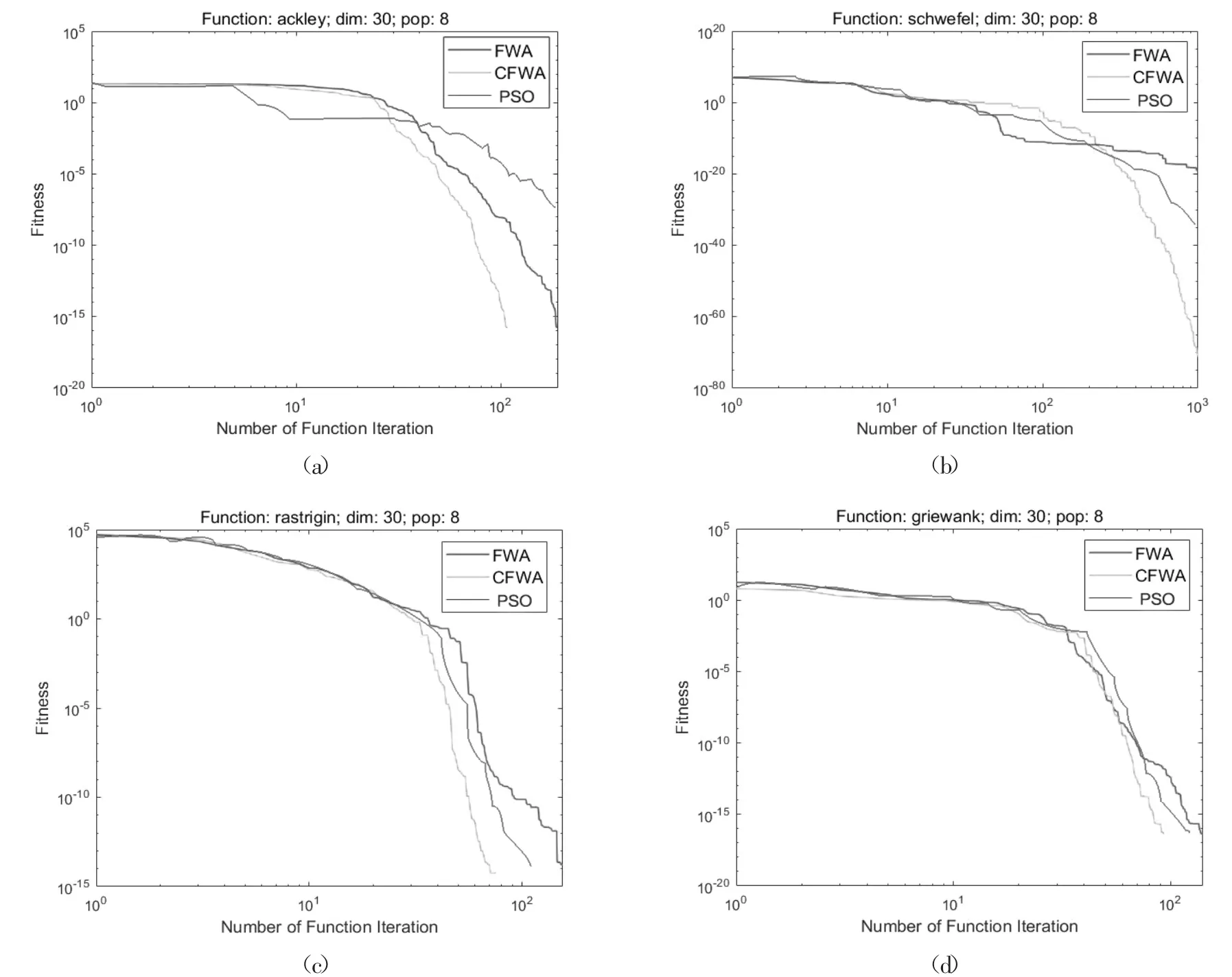
图1 仿真实验结果

3 农产品运输调度过程

3.1 农产品运输调度编码方式

3.1.1 编码策略

农产品物流运输调度属于离散调度问题，而基本的烟花算法仅适用于连续域空间搜索，所以使用编码策略实现连续空间到离散空间的映射，使离散机制在农产品运输调度过程中进行实时编码，本文采用农产品库车辆数与最大位置法相结合的方法进行编码，基于烟花算法是随机产生一个N维粒子空间，假设烟花维度为k=L+A-1，烟花i在空间中的个体位置为：xi=（xi1，xi2，xi3，xi4，xi5，…xik），我们把K的最小值设为1，从小到大排序（1，2，3…n），如果K的位置相近，优先从左开始编码，最后可得可把烟花的位置映射为（1，2，3…k）。

3.1.2 解码策略

对于有A个农产品库，且每个农产品库的车辆数为La，这些车辆需要配送B个客户点，解码步骤如下：

对于烟花i 经过最大位置法编码后得到如下序列，xi=（xi1，xi2，xi3，xi4，xi5，…，xik）。

（1）用“0”来代表农产品库点，如果xnj的值比农产品库的数量A大，则等同于“0”，也表示为农产品库点。

（2）初始解应该由车辆数L、农产品库数A、客户数量B以及一些辅助数字“0”构成。

（3）辅助数字“0”加在编码得到的烟花位置序列前后，用来分割路径。

（4）这些辅助数字“0”位于每个农产品库的客户和下一个农产品库之间。数字“0”之间的农产品库点构成了车辆的配送路径。

（5）一条完整的序列可以看作“L”个车辆的配送路径。

如果该农产品物流调度模型中7 个农产品库，有2 辆车，则A=7、L=2、k=8。经过最大位置法编码得到（2，1，4，7，8，5，3，6），在其首尾加上辅助数字“0”，为（0，2，1，4，7，8，5，3，6，0）。序列中8 大于A，则为农产品库点，车辆数为2，则它们的配送路径分别为0→2→1→4→7→0 和0→5→3→6→0。

3.1.3 适应度评估函数

烟花算法中通过适应度大小来评估烟花质量的优劣，适应度差的爆炸半径大，爆炸个数小；适应度好的爆炸半径小，爆炸个数多。在本文中适应度应该反映出车辆的运输成本距离等基本信息，因此，用式（3）来计算烟花的适应度值。

3.2 调度过程

步骤1：初始化，首先初始化算法中烟花种群数N，爆炸因子R，爆炸火花数量Si，爆炸半径Ai，高斯火花数M。

步骤2：初始烟花位置并进行编码，解码。

步骤3：根据式（2）计算每个烟花的适应度值，计算当前位置的烟花个体及其目标函数值，并统计当前最优位置及函数值。

步骤4：对烟花种群进行爆炸操作和变异操作，爆炸火花数和爆炸半径根据式（10）和式（16）来计算，高斯变异操作根据式（12）来计算。

步骤5：从候选种群（烟花、爆炸火花、变异火花）中选择N个烟花作为下一代种群，选择策略为精英-随机策略。

步骤6：根据2.2.2 提出的选择策略计算下一代烟花个体，直至达到最大迭代次数；若没达到则返回步骤3，直至输出最优解。

4 仿真分析

4.1 实验环境

为了验证改进的烟花算法（CFWA）在农产品调度问题中的有效性和可行性，进行仿真实验，实验运行环境为Windows10 系统，处理器Intel（R）Core（TM） i5-8400 CPU @ 2.80GHz，内存8GB，搭载MATLAB 2020b。

4.2 实验参数设置

本文用两组实验数据进行仿真实验。第一组数据（P1）包括5 个农产品库点、12 个客户点；第二组数据（P2）包括6 个农产品库点、20 个客户点。将实验参数设置为烟花种群数N=5，爆炸火花数为S=150，爆炸半径A=1500，高斯变异火花数M=40，最大迭代次数为1000，获取最优烟花次数为20。为了确保数据的科学性，将每个算例独立运行10次的平均值进行统计。

P1 的具体信息如表1、表2 所示，P2 的信息如表3、表4 所示。

表1 第一组农产品库信息表

表2 第一组客户点信息表

表3 第二组农产品库信息表

表4 第二组客户点信息表

4.3 实验结果

本文通过对FWA、CFWA 和PSO 进行对比实验，计算适应度值，统计算例10 次运算所得到的数据如表5 所示。

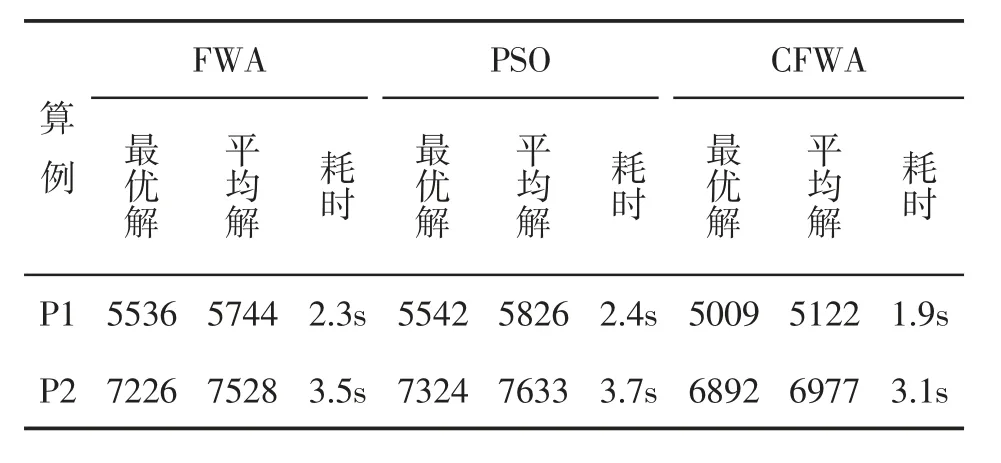
表5 FWA、CFWA 和PSO 的实验对比

从表5 中可以看出，在P1 和P2 算例各计算10 次的情况下，CFWA 比FWA 和PSO 所耗费的时间更少。此外CFWA 的最优解也比FWA 和PSO更优，P1 中CFWA 分别比FWA 和PSO 优化了527、533；P2 中CFWA 分别比FWA 和PSO 优化了334、432。在平均解上CFWA 也比FWA 和PSO 更优。上述实验结果显示，在相同的实验参数条件下，CFWA 的最优解和平均解优于烟花算法和粒子群算法，而且耗时也相对少。这说明CFWA 对爆炸半径进行混沌操作，增强了烟花的全局搜索能力，提高了问题的求解精度和效率。

5 结语

本文考虑到农产品运输中的车辆运输重量、运输时薪、运输底薪、服务时间等约束性条件。对农产品物流运输调度问题建模，采用车辆数与最大位置法相结合的编码方式，提出了一种混沌烟花算法CFWA。实验结果表明：CFWA 增强了算法的多样性和全局搜索能力，能够有效求解该模型，与基本的烟花算法及粒子群算法相比，CFWA 具有更好的寻优性和求解精度。