适用于水轮机调节的改进滑模控制研究

王瑞明，赵红玉，马振兴

（喀什大学物理与电气工程学院，新疆 喀什 844000）

水电是一种可开发程度最高的清洁能源。在未来相当一段时间内，水电是我国最主要的可再生能源和应对全球气候变化的重要手段[1]。间歇性的可再生能源会对电力系统的调频调峰产生巨大压力，未来水电“调节器”功能将超越能源[2]。水轮机是水电厂电能生产的主要动力设备。为了保证供电质量，水轮发电机组运行过程中必须根据负荷的变化调节水轮发电机组有功功率输出，维持水轮发电机组的转速在规定范围内。水轮机调节系统是非线性系统，非线性特性表现为其主动力矩和过流量用非线性数学表达式来刻画[3]。水轮发电机组模型参数随运行工况也会发生较大变化。传统的水轮机PID 调节参数需经过现场试验确定，在运行过程中还需随运行环境的变化不断优化[4]。智能控制的水轮机调节系统，需要通过对水轮发电机组参数辨识、运算后，再对水轮发电机组进行控制，辨识和运算需要大量在线或离线学习训练[5]。另外，传统控制方法的设计思想是将控制设计在一个特定运行点上，导致系统在运行中，很难适应系统的各种工况变化[6]。滑模变结构控制对控制对象的不确定性和扰动具有较强的鲁棒性，在水轮机转速调节控制中有较大的发展潜力，是一种鲁棒控制策略[7]。由于水轮机系统外部扰动和模型不确定是传统滑模控制应用于水轮机调节产生抖振的主要原因[8，9]。传统滑模控制中滑模面的摄动越大，滑模控制抖振振幅越大，影响滑模面摄动的主要原因是状态变量误差[10，11]。由于水电机组中的水锤效应，作为传统滑模控制对象的水轮机系统表现为非最小相位系统[12，13]。以上这些原因限制了滑模控制在水轮机转速调节系统中的应用。为克服以上传统滑模控制应用于水轮机调节控制中的缺点，本文以水轮机调节系统为对象，通过求解线性矩阵不等式，构建状态反馈增益控制器[14]，优化状态反馈增益，设计了水轮机组转速跟踪控制律，减小滑模控制抖振。过软件仿真验证该控制策略能够减小滑模控制输出抖振，而且可有效控制和消除水轮机调节系统的跟踪误差。

1 系统建模

工程实际中，选择水轮机系统容易测量的水轮机转速x、电液随动系统接力器行程y、水头h作为状态变量。用状态方程描述的水轮机系统为[15]

式中：eqh、eqx和eqy分别为水轮机过流量的水头、转速和接力器行程系数，eh、ex和ey分别为水轮机主力矩的水头、转速和接力器行程系数，q、mt、h、x和y分别为水轮机过流量、主力矩、水头、转速和接力器行程的偏差相对值。电液随动系统的输入为水轮机控制系统的输出u，Tw为水流惯性时间常数，T′a为发电机组及其负载转动部分的惯性时间常数，mg0为额定频率下发电机负载转矩偏差相对值，eg为发电机负载转矩对转速的传递系数，式中eg为机组的综合自调节系数，en=eg-ex。写成矩阵形式，得

式中：X为状态向量，X=[xyh]T，系数矩阵

输出

U=[u]

扰动

2 基于LMI 的滑模鲁棒控制器设计

本文利用线性矩阵不等式算法，将水轮机控制系统中的状态反馈测量误差问题转化为线性矩阵不等式约束优化问题。通过线性矩阵不等式，求得水轮机转速、主接力器行程和水头等状态量的增益，对水轮机转速进行有效控制。

2.1 调节器设计

为有效对状态变量进行调整，设计动态补偿算法为[16]

式中z为动态补偿变量，M为补偿系数，待求矩阵。

选择滑模函数为

式中K为待求矩阵，须满足KG=I。对式（4）两边求导，将式（2）、式（3）代入式（4），得

控制律设计为

式中：η为切换增益，η=（η1η2η3）。

有

在滑模控制实施中式（4）满足滑模条件，即当t＞t0时，s=0，则z=-Kx，将式（4）、式（7）代入式（2）得

令E=F+G（K-KF-M）。

定理：设P为正定对角矩阵，如果满足不等式

由被控对象式（2）和控制律式（7）构成的闭环系统渐进稳定。

证明：取Lyapunov 函数为

V=xTPx（10）

则有

将式（8）代入式（11），得

当FTP+PF＜（K-KF-M）TGTP+PG（K-KF-M）时，有V˙＜0，系统是渐进稳定的。求解线性矩阵不等式，可解得矩阵K和M。

2.2 跟踪控制器设计

定义跟踪误差e为

式中：xd为期望状态；e1为水轮机实际转速与期望转速的误差，e2为水轮机接力器实际行程与期望行程的误差；e3为水轮机实际水头与期望水头的误差，得

设计控制律为

设d=（d1d2d3）T，式中：d1、d2、d3为d中各元素，η中各元素的取值满足ηi＞di，i=1、2、3。将式（16）代入式（15）得

引理：设P为正定对角矩阵，如果满足不等式

由被控对象式（2）和控制律式（16）构成的闭环系统渐进稳定。

证明：取Lyapunov 函数为

可得

将式（17）代入式（20），可得

由于式（16）中η中各元素的取值满足ηi＞di，所以

则有，当满足以下条件

3 仿真验证和结果分析

3.1 仿真验证

本文中的水轮机选定GZ990 型；其中的参数根据相应水轮机的特征曲线依次为：ey=0.9，ex=-0.5，eh=1.2，eqy=0.55，eqx=0.65，eqh=0.2，eg=2.0，T′a=1.5，Tw=2.4，Ty=0.2。初始状态参数：水轮机主力矩和转速的标幺值为1，主接力器行程的mg0为0.79。状态方程式（6）中的矩阵F、G和d分别为

根据上述1 节的数学模型，在MATLAB 软件的SIMULINK 中建成仿真模型。控制律式（13）中的切换增益η=[50 50 50]T，边界层取0.05。对基于线性矩阵不等式的水轮机转速调节改进滑模控制策略进行仿真研究。通过监测水轮机转速速跟踪阶跃信号的响应速度、水轮机转速跟踪阶跃信号和正弦信号跟踪误差、控制器输出抖振大小来判断其有效性，对传统的滑模控制和本文设计的改进的滑模鲁棒控制策略进行仿真分析。

3.2 仿真结果分析

通过MATLAB 仿真软件工具包YALMIP 求解线性矩阵不等式式（16），求得矩阵K和M唯一解，分 别 为M=[5.709 3 1.486 5 9.603 7] ，K=[4.735 93.968 9 1.912 6] 。设置两种转速给定输入，即阶跃输入和正弦输入。分别以转速给定阶跃指令n（t）=1（t）r/s 和正弦指令n（t）=sin（4t）r/s 为给定信号，通过比较传统滑模控制和改进滑模控制的水轮机调节系统转速跟踪性能。

传统滑模控制水轮机调节系统转速阶跃信号和正弦信号跟踪见图1。图1 中横坐标为时间t，单位为秒s，纵坐标为水轮机给定转速nd和实际跟踪转速n，单位为r/s。从图中水轮机转速跟踪曲线可看出，水轮机转速稳定后，水轮机转速阶跃跟踪和正弦跟踪有明显误差。本文设计的改进滑模控制水轮机调节系统转速阶跃信号和正弦信号跟踪见图2。图2 中横坐标为时间t，单位为s，纵坐标为水轮机给定转速nd和实际跟踪转速n，单位为r/s。从图中水轮机转速跟踪曲线可看出，水轮机转速稳定后，阶跃跟踪和正弦跟踪误差明显减少，但是响应速度变慢。图3 对比了传统滑模控制器和本文设计的改进滑模控制器水轮机调节系统转速跟踪性能。图3 中横坐标为时间t，单位为s，纵坐标分别为水轮机跟踪信号和正弦信号的实际转速n，单位为r/s。仿真结果表明本文设计的改进滑模控制的转速跟踪明显优于传统滑模控制的转速跟踪。由于本文设计的改进滑模控制器在水轮机转速调节过程中，涉及线性矩阵不等式的求解，本文设计的改进滑模控制器响应速度较传统滑模控制器慢。图4 对比了传统滑模控制和本文设计的改进滑模控制水轮机调节系统转速跟踪误差。图4 中横坐标为时间t，单位为s，纵坐标为水轮机转速跟踪误差e=nd-n，单位为r/s。从图4中可以看出，水轮机转速稳定后，改进滑模控制策略的不管是跟踪阶跃信号，还是跟踪正弦信号，改进滑模控制策略比传统滑模控制策略的跟踪误差明显减小。图5 给出了传统滑模控制和本文设计的改进滑模控制在阶跃信号和正弦信号输入下控制器的输出曲线。图5 中横坐标为时间t，单位为s，纵坐标为控制器输出u，单位为A。从图5 中可以看出，水轮机转速稳定后，传统滑模控制器的控制输出存在有较大的抖振，本文设计的改进滑模控制器的控制输出抖振现象明显减小。通过仿真表明，基于线性矩阵不等式的改进滑模控制器具有较高的转速跟踪精度、控制器输出抖振较小的优点。

图2 改进的滑模鲁棒控制水轮机转速跟踪曲线

图3 滑模控制和改进的的滑模鲁棒控制水轮机转速跟踪曲线

图4 滑模控制和改进的滑模鲁棒控制水轮机转速误差曲线

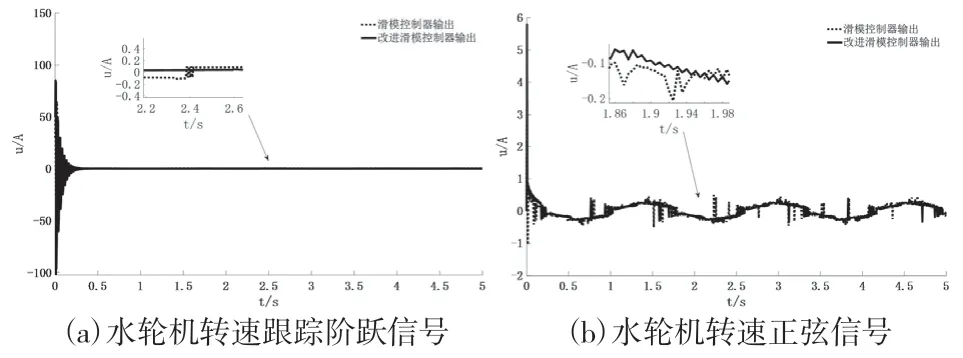
图5 滑模控制和改进的滑模鲁棒控制的控制输出曲线

4 结论

基于线性矩阵不等式的改进滑模控制水轮机转速调节系统得出结论如下：

（1）与常规滑模变结构控制系统相比，本文设计的改进滑模控制水轮机调节系统具有跟踪误差小、控制输出抖振小以及能快速跟踪给定转速的优越性。

（2）减少传统滑模控制中水轮机调节系统转速、接力器行程和水头等状态量的测量误差对滑模控制输出抖振的影响，并利用李雅普诺夫稳定性理论证明改进滑模控制策略的有效性。因此，将基于线性矩阵不等式的改进滑模控制策略应用于水轮机调节系统中具有一定的应用前景和工业价值。

（3）传统单一控制水轮机调节控制策略大都存在一定局限性。基于线性矩阵不等式的改进滑模控制水轮机调节系统是较复杂的控制系统。将鲁棒控制算法与传统控制算法相结合的复合控制策略将是未来水轮机转速调节系统控制策略的研究方向。

参考文献：

[1] 吴先俊，郭成．基于智能安全帽的大型水电工程安全智能管控技术[J]．人民黄河，2021，43（S1）：218-220．

[2] 聂常山，赵宇瑶，王延红．南水北调西线一期工程效益分析[J]．人民黄河，2020，42（6）：120-124．

[3] 冯国顺，李家新，邹象斌． 乌东德水电站水轮机调速器监造质量控制要点[J]．人民黄河，2021，43（S1）：272-275．

[4] 史华勃，陈刚，丁理杰，等．兼顾一次调频性能和超低频振荡抑制的水轮机调速器PID 参数优化[J]．电网技术，2019，43（1）：221-226．

[5] 卢恒光，温步瀛，李天扬．基于模糊神经网络的水轮机调速器PID 控制[J]．电网与清洁能源，2021，37（5）：128-133．

[6] 戴磊，李洋洋，尤钱亮，等．基于LMI 算法的永磁同步电机混沌最优控制[J]．水下无人系统学报，2021，29（3）：293-298．

[7] 田钧，郑里鹫，龙飞．基于动态补偿的小型涡扇发动机滑模控制[J]．自动化与仪表，2020，35（4）：11-15，24．

[8] 付文龙，张仕海，郑阳．水轮机调节系统的动态滑模控制[J]．中国农村水利水电，2023（2）：211-217，225．

[9] 黄鑫，王婕，邢侃．基于滑模控制的新能源电网环境下水力发电机组控制方法[J]．水利水电技术，2020，51（12）：141-149．

[10] 吴道平，鄢波，刘冬，等．适用于水电机组的改进滑模控制策略研究[J]．水力发电学报，2020，39（10）：82-91．

[11] 薛晗，邵哲平，潘家财．基于线性矩阵不等式的船舶动力定位滑模控制[J]．交通运输工程学报，2018，18（5）：119-129．

[12] 潘熙和，高雄，方斌臣，等．大型冲击式水轮机调速系统在云南高桥水电厂的应用[J]．水利水电快报，2022，43（12）：88-92．

[13] 寇攀高，朱光明．负载工况水轮机变速运行仿真研究[J]．水力发电学报，2022，41（9）：87-97．

[14] 张银锋，邵英，李陆军．基于LMI 方法的中频电源的动静态和鲁棒性能优化控制[J]．海军工程大学学报，2022，34（4）：80-86．

[15] 徐枋同，李永华．系统辨识理论与实践—在水电控制工程中的应用[M]．北京：中国电力出版社，1999．

[16] 万慧，齐晓慧，李杰．基于线性矩阵不等式的线性/非线性切换自抗扰控制系统的稳定性分析[J]．上海交通大学学报，2022，56（11）：1491-1501．

[17] 刘金琨．滑模变结构控制MATLAB 仿真基本理论与设计方法[M]．北京：清华大学出版社，2019．