基于随机森林算法的虚拟仿真实验室仪器故障预警方法

李梅琴

(闽西职业技术学院 实训实验管理中心，福建 龙岩 364021)

虚拟仿真技术在仪器分析和操作中具有非常明显的应用优势,为现阶段强化仪器管理提供了虚拟实验室系统操作的概念。邓雅琼等[1]提出仪器分析的虚拟仿真平台设计方法,在虚拟实验室环境中,对设备应用及分析进行教学和管理,保障操作的重复性和准确性。而在现阶段高校教育中,同样存在仪器设备不足和难以观察的问题,影响教学效果,以此提出虚拟仿真实验室的概念,为教学提供了全新方式。黄科等[2]分析了虚拟仿真实验室建立的必要性,并对虚拟仿真技术的应用方式作出假设,为实验室的建设和管理提供了一定参考。

无论是现实仪器应用还是虚拟实验室环境中的仪器应用,都需要对其进行全方位的管理,以确保仪器能够安全地进行多种类型的操作。其中对故障预警的设计是仪器管理中较为重要的一个环节,樊红卫等[3]提出一种基于转子振动频率的故障预警方式,解释了典型故障的原因和诊断机理及对振动频率的引用,可以非常清晰地模拟转子的不平衡与不对中的状态,能够对设备的故障类型做出自动判断。钟少恒等[4]提出了随机森林的算法清洗方式,以多维分布的节点构建随机处理模型,对故障信息进行特征采样。

本文以上述研究为基础,研究随机森林算法的故障预警方法,为虚拟仿真实验室的仪器管理提供理论支持。

1 虚拟仿真实验室仪器故障预警

1.1 集成神经网络对应仪器故障特征

虚拟仿真实验室中的仪器,在连接和组成结构上,与真实仪器的摆放形式一致,能够真实地还原设备现场的操作环境。当其出现故障或者问题时,同样需要按照现实标准进行判断,以为常规条件下仪器的应用提供参考。故障特征信号在传递过程中,以文件形式为存在标准,通过索引号和通道号以及量值等信息,预估出报警上限和报警下限,判断实验室仪器的运行状态,并加以说明。

设置诊断子网络个数为p,与决策融合网络构成一体的综合网络形式,即集成神经网络,能够诊断出q种类型故障[5]。

集成网络用WW1来表示,其中输出的不稳定信号为故障向量,表示为

Er=(er1,er2,…,ert)q,

(1)

故障向量Er映射后,转换为

Er=fr(Yr),

(2)

式中:fr表示映射函数,r=1,2,…,p;Yr表示网络WW1的特征向量。

故障特征量融合的过程实际上就是故障信号输出的过程,以每个子网络中的输出量对应融合网络中的节点信息,将WW1中的输出节点个数设置为wr,则融合网络中的决策点个数表示为[6]

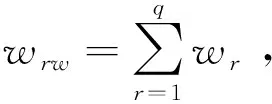
(3)

融合网络中的决策信息输出结果为

E=f(Y1+Y2+…+Yn)。

(4)

以此寻求神经网络中的训练样本,将前置子网络中的所有数据信息点进行汇总,当决策网络中的样本数据来源于前置网络时,即可设定两个网络之间的特征相匹配。

将网络WW1的故障向量设置为集合Ar=[ar1,ar2,…,art],每一种故障对应的置信权值向量Sr=[Sr1,Sr2,…,Srt],子网络的并行组合向量集Wp=[WW1,WW2,…,WWp],以此建立故障特征矩阵A为[7]

(5)

置信权值矩阵S为

(6)

此时融合网络输出为

E=A·S。

(7)

由此对实验室仪器故障类型进行判断,将产生的不同种类故障特征进行分析,以集成神经网络的有机整体,在多组相互独立且配合的模块中,实现特征的在线提取和划分,并通过森林算法构建预警模型。

1.2 随机森林算法构建预警模型

集成神经网络的实现借助于信息分配网络的构建,以多个信号为基础,对应实验室仪器故障诊断,将部件级别的信号进行定位[8]。与现阶段个体网络诊断不同,集成神经网络能够真实还原故障定位,对故障点的信号完成标识。

从数学专业角度,将随机森林算法引入故障诊断中,定义特征决策树,设置即将需要分类的故障类型,对某一类的信息值进行计算,公式为

Z(C=cr)=-lbX(cr),

(8)

式中:Z(C)表示实验室仪器的随机监测数据变量;X(cr)表示某一类信息cr出现的概率。

对随机变量的不确定度量,可以采用信息熵,即该故障特征的期望值,表示为[9]

(9)

式中g表示仪器故障的分类数量。

信息熵完全依赖于C的分布,与其参数取值没有联系,基本上与C=cr出现的概率呈反比趋势,其值越大,表示故障分类的准确性越低。当随机选择两个变量时,其与概率之间的变化关系如图1所示。

图1 信息熵与概率的变化关系

根据图1内容所示,横坐标表示为概率,纵坐标表示为信息熵,当横坐标的值取0或者1时,其纵坐标的对应值均为0,表示随机变量完全没有不确定性[10]。而取值为0.5时,纵坐标值为1,即随机变量的不确定性达到顶峰。以此将熵概念引入特征分类中,对仪器的故障类型进行判断,对随机变量进行定义,都设置为F,在变量条件C下的不确定性,即为判断概率,表示为

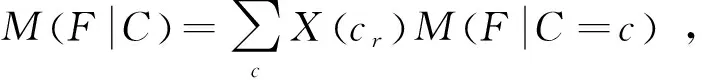
(10)

式中:M(F|C)表示联合熵;M(F|C=c)表示单独的熵[11]。在C和F共同满足信息类型时,能够在给定条件下,对故障问题做出预警信号,借助递归形式,对上述特征进行组合,当出现故障时第一时间完成预警。

1.3 递归形式组建分类树预警故障

仪器设备在运行过程中只会出现两种结果,一是正常工作状态,二是故障状态,而在不同事件中产生的随机事件可能为正常工作,也可能为故障状态。因此采用随机森林的方式进行故障预警,可以将两种状态作为随机时间,而{正常,故障}集合则为随机森林算法的样本空间。但常规模式下数学计算过程不会用正常和故障两种字眼作为数学运算的介质,本文用1表示故障,0表示正常[12-13]。

对给定的样本数据能够分类出的信息期望做出假设,即信息熵,利用式(8)可表示为

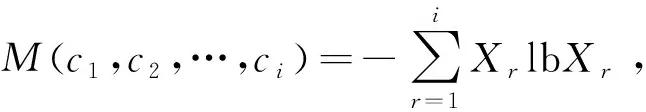
(11)

当样本数据中包含多种特征属性时,定义k个特征属性构成集合为KL(L=1,2,…,k),每个特征属性均含有H个数值。特征属性KL将J划分成k个子集,分别为J1,J2,…Jk。假定属性KL中子集Jk的类Cr的样本数用drk来表示,则由属性KL划分的子集熵值的计算公式为[14]

(12)

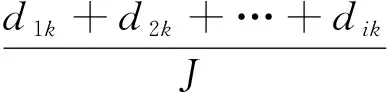
(13)

式中:GR表示增益效果;Gn表示信息增益;SI表示信息类型。

对故障特征属性KL分类出的判断结果代表信息类型,可用SI(J,KL)来表示,具体为[15]

(14)

按照信息增益的最大原则,对不同仪器设备随着分类得出的判断结果进行标记,联系故障信号特征与某个仪器之间的关系,确定故障位置进行预警。至此在随机森林算法下,完成了对虚拟仿真实验室仪器故障的预警方法设计。

2 实验测试与分析

本文设计了随机森林预警方法,对虚拟实验室仪器故障进行监测,为验证其实际应用价值,选择两组传统方法进行对比,测试不同预警方法的应用效果。

2.1 获取实验数据

故障信号预警的基本前提,就是对故障信号频率的预估准确度。为验证三种不同方法的预警效果,选择某虚拟仿真实验室仪器为测试对象,对其故障信号频率进行预估。

将信号采样率设置为4 000 Hz,采样点数量为2 024个,随机选择余弦信号下对应的故障频率,进行全局频谱图绘制,如图2所示。

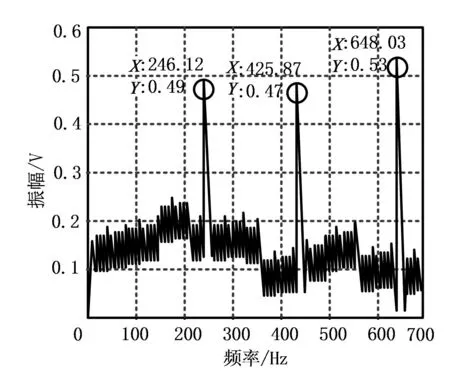
图2 采样点信号全局频谱图

根据图2内容所示,此次设计的仪器故障信号频谱存在三组余弦信号极值,故障信号表示为

I=cos(2πf1t)+cos(2πf2t)+cos(2πf3t),

(15)

式中f1、f2和f3的取值分别为246.12、425.87和648.03 Hz。将上述频率作为测试对象,代入预警方法中进行测试。

2.2 余弦信号下故障信号频率预估对比

分别将三种预警方法连接到仪器设备中进行频率预估,对故障信号进行局部细化处理,如图3所示。

(a)246.12 Hz

根据图3内容所示,在不同故障频率的细化频谱下,本文方法对应的数据基本与原始采样点数据一致,而两组传统方法存在一定偏离。

为更清晰地展示预估精度,将故障信号的实际频率和估计频率进行汇总,统计各信号与真实数据之间的差值,见表1。

表1 不同方法预估误差 单位:Hz

根据表1内容可知,本文方法的估计误差可以控制在0.002 5 Hz以下,两组传统方法的估计误差分别为0.2 Hz和0.15 Hz。

2.3 不同信噪比下故障频率预估对比

在此基础上对故障信号加入噪声,以不同信噪比变化为条件,从-10到10 dB,验证三种预警方法的频率预估能力。

以4 dB为间隔,在三种预警方式下,获取三组信号的估计频率,如图4所示。

根据图4内容所示,随着信噪比的加入,故障信号的预估频率也发生变化,在本文方法下对故障信号的频率预估逐渐趋向实际数值,最大误差只有0.080 1 Hz。而两组传统方法下,当加入噪声后对信号频率的预估会出现较大误差,对故障信号的预警会出现延迟现象,说明本文方法更加有效。

3 结束语

本文以随机森林算法为基础,按照对信息熵和信息增益的处理原则,重新划分实验室仪器的故障类型,完成不同特征信号的定位匹配,设计一种新的仪器故障预警方法,主要结论如下:

1)不同故障频率的细化频谱基本与原始采样点数据一致,故障信号的频率预估逐渐趋向实际数值,最大误差只有0.08 1 Hz,能够对不同的故障类型进行精确匹配。

2)估计误差可以控制在0.002 5 Hz以下,及时发出故障预警信号,保障仪器的稳定运行,具有实际应用效果。

由于本文在对故障测试样本选择上能够对比的选项较为单一,所得结果具有一定偏差,后续研究针对不足之处,进行更深层次的改进,对非平稳信号或者信息较大的信号进行划分,提出适用于多种类型的预警方法。