基于统一解的重叠盾构隧道施工土体变形研究

魏 纲,朱德涵,赵得乾麟,王 哲,郭丙来

(1.浙大城市学院 浙江省城市盾构隧道安全建造与智能养护重点实验室,浙江 杭州 310015;2.浙大城市学院城市基础设施智能化浙江省工程研究中心,浙江 杭州 310015;3.浙江工业大学 岩土工程研究所,浙江 杭州 310014;4.广州南沙资产经营集团有限公司,广东 广州 511466)

随着城市隧道网线的逐渐密集,重叠隧道的出现变得常见。相较于单线和双线平行隧道,重叠隧道由于开挖面排列方式的不同,大大增加了隧道穿越不同土层的概率,复杂的土质条件使得盾构施工引起的土体变形结果更难预测。此外由于重叠盾构隧道双线邻近的施工特点,开挖面附加推力、盾构机侧壁摩擦力以及注浆压力等多重因素叠加所产生的土体变形,相较于单线隧道更为显著。若不能准确预测土体变形,将对周边建筑与行人车辆产生巨大的安全隐患,因此有必要对重叠盾构施工引起的土体变形展开研究。

目前,针对重叠盾构隧道施工引起土体变形的研究方法可分为经验公式法[1-3]、解析理论法[4-5]、边界单元法[6]、有限单元法[7-8]、模型试验法[9-11]等。关于经验公式法,现有研究主要通过Peck公式[12]的叠加来计算重叠盾构引起的土体变形,然而Peck公式仅限于单一平面内的横向土体变形计算,对于三维空间内土体变形的预测,尚且存在局限性。解析解方面,周烨波等[4]采用随机介质理论,通过叠加的方式对土体变形进行计算;魏纲等[5]采用了二维的统一土体移动模型解[13](以下简称统一解),然而该方法仅能计算单一横断面内土体损失导致的土体变形,且没有考虑土质条件对纵向土体变形的影响。隧道施工是一个多重因素相互作用的过程[14-16],因此针对除土体损失外的其他因素有以下研究:魏纲[17]通过Mindlin解[18],推导了正面附加推力和盾壳与土体之间的摩擦力引起的地表土体变形计算公式;卢海林等[19]考虑了注浆压力影响下单线隧道盾构施工引起的土体变形计算方法;洪杰[20]结合以上研究在双圆盾构开挖中综合考虑了正面附加推力、盾壳摩擦力和注浆压力;王霄[21]也将以上因素的计算方法应用于双线盾构施工的土体变形计算中。综上所述,现有研究尚未考虑土质条件对纵向土体变形的影响,且针对重叠隧道的统一解计算方法未考虑除土体损失外的其他因素对土体变形的影响,因此有必要对重叠盾构隧道施工引起的土体变形计算方法作进一步研究。考虑土质条件对纵向土体变形的影响,笔者对三维统一解[22]进行修正,并建立三维重叠隧道计算模型,将统一解应用于重叠盾构施工土体损失造成的土体变形的计算中,此外采用Mindlin解求得开挖面附加推力、盾壳摩擦力以及注浆压力3种因素对土体产生的变形量,将以上因素与土体损失的计算方法叠加,最终得到多因素影响下重叠隧道盾构施工引起的土体变形计算方法。将公式代入实际工程案例进行验算,验证笔者方法的可行性。

1 研究方法

1.1 现有方法及不足之处

魏纲[22]基于Sagaseta[23]提出的地表纵向变形计算公式,结合Peck公式提出在既定工况下,土体损失率与地表最大沉降量成正比的结论,推导出随轴线上方计算点与开挖面间距x变化的土体损失率η(x)的计算公式,将公式代入二维统一解公式[13],得到土体变形三维统一解[22],然而该方法仍存在以下不足:

1) 为研究土质条件对纵向沉降曲线的影响,同时尽量减少隧道上覆土体厚度的影响,表1列举了8组洞径比(轴线埋深h与隧道直径D的比值)较为接近的监测数据。将土体沉降起始点与开挖面间的距离减去沉降结束点与开挖面的距离,得到纵向土体变形稳定所需的距离(开挖面掘进方向为正,反之为负)。通过比较稳定距离,发现土质偏好的土体沉降稳定距离普遍要长于土质较差的土体,其原因可能是土质较为良好的土体由于颗粒间内摩擦角较大,导致土体在盾构施工过程中下落较慢,从而产生的地表纵向变形曲线会更为平稳,稳定距离更长,而土质较差的土体回落较快,因此形成的纵向地表变形曲线更为陡峭。然而在三维统一解中,当隧道埋深确定时,纵向土体损失率η(x)仅与最终沉降稳定处的最大土体损失率η有关,尚未考虑土质条件对纵向土体变形曲线的影响,这与实际情况不符。

2) 目前,三维统一解多用于单线盾构隧道施工引起的土体变形计算,无法直接用于重叠盾构隧道引起的土体计算中。因此,需针对重叠隧道建立三维统一解的计算模型。

3) 盾构施工引起的土体变形是多种因素共同影响的结果,重叠隧道由于双线紧邻的特殊施工要求,使得各种因素对土体变形的影响都显著增加。而三维统一解仅考虑了土体损失对土体变形的影响,未考虑其他因素,使得计算结果与实测值差距较大。

1.2 针对不足之处进行改进

1) 为考虑纵向土体条件,需对三维统一解中土体损失率计算公式进行修正,原土体损失率的计算式为

(1)

添加修正参数m,用mx代替原式中的x,修正后的土体损失率计算式为

(2)

式中:x为计算点与开挖面间的水平距离(掘进方向为正);h为隧道轴线埋深;m取值为(0,+∞)。土体损失率曲线会随着m值的增大而变陡,当纵向土质较好时,m的取值会偏小,土体损失率曲线也变得平缓;当m=1时,式(2)与式(1)相同。

2) 将上、下线土体变形量相叠加,得到重叠工况下三维土体变形的计算公式;为符合实际工程情况,计算时还需考虑先行线与后行线开挖面间的距离。

3) 为考虑多种因素对土体变形的共同作用,利用Mindlin解计算盾壳摩擦力、开挖面附加推力以及注浆压力3种因素产生的土体变形量,将上下线的变形量相叠加,再与三维统一解结合,得到最终的计算方法。

1.3 计算模型建立

重叠盾构隧道的力学计算模型如图1所示,图1中:h为隧道轴线埋深;R为盾构机外半径;L为盾构机长度;P1,P2,P3分别为盾构正面附加推力、盾壳摩擦力和注浆压力;下标u,d分别代表上、下线的对应参数;若xu,xd分别为某处土体以上线和下线隧道开挖面中心为原点的轴向坐标,K为两条隧道开挖面的相对距离,则xu+K=xd,先上线后下线开挖时K为正值,反之为负值。

图1 重叠隧道计算模型图

由于盾构隧道施工是一个多重因素共同作用的复杂工程,为便于计算,作以下假定:1) 盾构隧道穿越的土体土质均匀,不排水固结,土体为线弹性半无限空间体;2) 盾构开挖面荷载为均布荷载,且作用面为开挖面的面积,盾壳摩擦力沿盾构机侧壁均匀分布,注浆压力沿管片环向均匀分布,以上因素互不干扰;3) 隧道轴线埋深固定,且盾构机沿轴线水平推进。

1.4 重叠隧道土体变形公式推导

1.4.1 土体损失引起的土体变形计算

将式(2)代入原三维统一解公式中,得到土体损失产生的任意点的土体变形,土体竖向变形计算式为

(3)

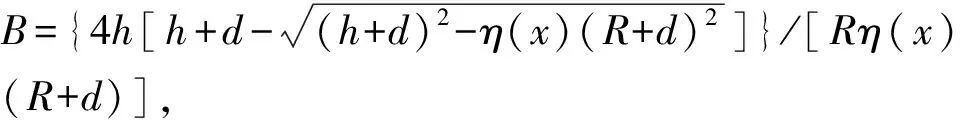
(4)

基于式(3,4),采用上、下线隧道土体变形相叠加的方法,得到重叠工况下的土体变形三维计算式。工况中任一点土体垂直方向(z轴方向)的计算式为

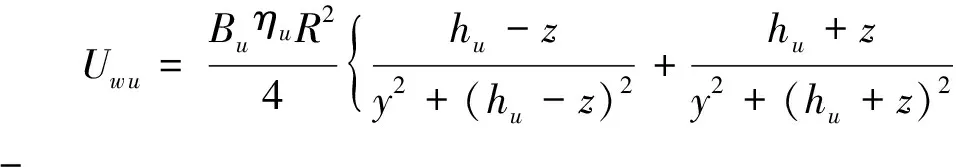
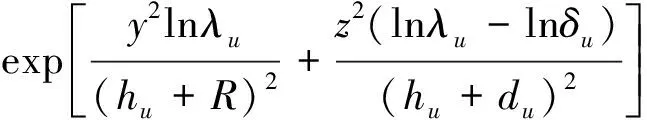
(5)

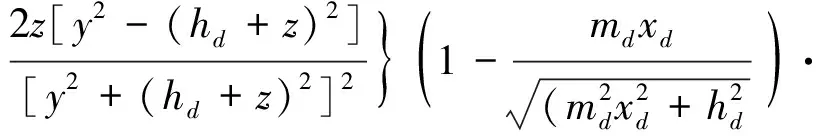
(6)

Uw=(Uwu+Uwd)

(7)

任意点土体水平变形计算式为

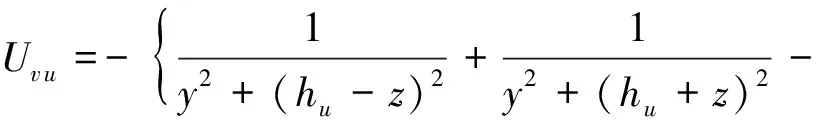
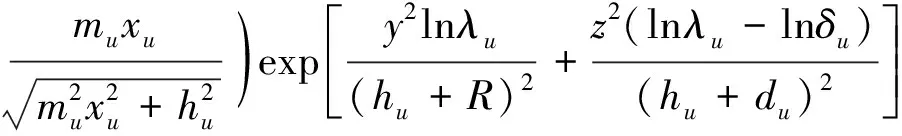
(8)

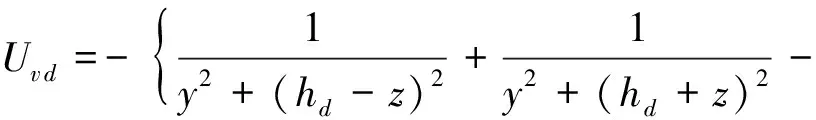
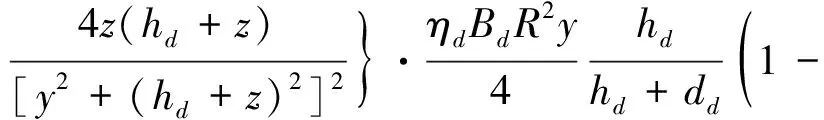
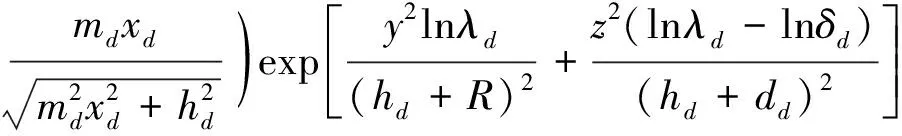
(9)

Uv=(Uvu+Uvd)

(10)

式中:Uwu,Uwd分别为上、下线的土体竖向变形;Uw,Uv分别为重叠隧道盾构施工土体损失引起的总土体竖向变形和横向变形;Uvu,Uvd分别为上、下线土体水平变形;土体参数m,η与d的取值通过Matlab软件反算得出,其余参数与上文一致。

1.4.2 正面附加推力引起的土体变形计算

根据Mindlin解,当沿x轴方向的单位集中力作用在(0,0,h)处时,在x轴方向引起的土体变形为

(11)

在z轴方向引起的土体变形为

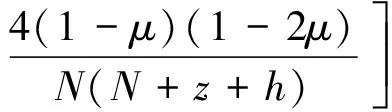
(12)

在y轴方向引起的土体变形为

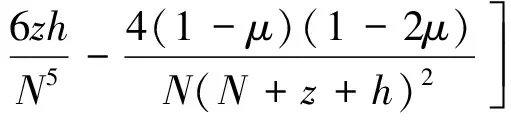
(13)

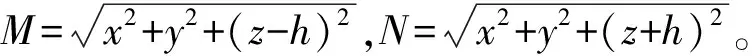
采用魏纲等[17]的方法,取dP1=P1rdldθ为开挖面上单位面积的附加推力,并通过文献[21]获得等效坐标,将单位力代入进行积分,得到上线隧道正面附加推力引起的z轴方向、y轴方向的土体变形分别为

(14)

(15)

同理,下线引起的z轴方向、y轴方向的土体变形分别为

(16)

(17)

式中:P1u,P1d分别为上、下线盾构的正面附加推力。叠加上下线的土体变形公式,得到正面附加推力引起总的土体竖向和横向水平变形分别为

w1=w1u+w1d

(18)

v1=v1u+v1d

(19)

1.4.3 盾壳摩擦力引起的土体变形计算

与上述思路相同,盾构机侧壁上单位面积受到的摩擦力为dP2=P2Rdldθ,代入Mindlin解进行积分,得到上线盾壳侧壁摩擦力引起的z轴方向、y轴方向的土体变形分别为

(20)

(21)

同理,下线z轴方向、y轴方向的土体变形分别为

(22)

(23)

式中:P2u,P2d分别为上、下线盾构机盾壳与土体之间单位面积的摩擦力。将公式进行叠加,得到重叠盾构隧道施工中盾壳摩擦力引起总的土体竖向和水平变形分别为

w2=w2u+w2d

(24)

v2=v2u+v2d

(25)

1.4.4 附加注浆压力引起的土体变形计算

通过洪杰[20]的方法,令附加注浆压力作用长度为b,土体受到集中力为dP3=P3Rdθdl,将沿衬砌环向发散的集中力分解为水平力dP3h=-P3cosθRdθdl和竖向力dP3v=-P3sinθRdθdl。分别进行计算,得到两个分力各自引起的土体竖向变形和水平变形,将所有同方向的变形进行叠加,得到上线盾构开挖时附加注浆压力引起的z轴方向、y轴方向的土体变形分别为

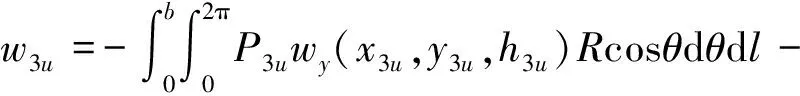
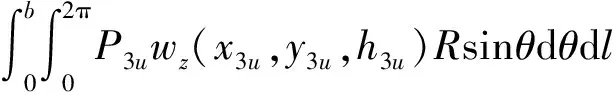
(26)

(27)

同理,下线引起的z轴方向、y轴方向的土体变形分别为

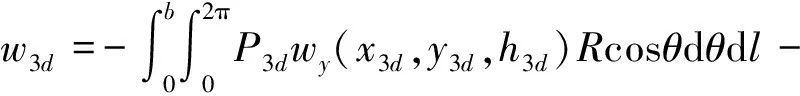
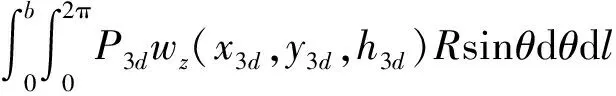
(28)

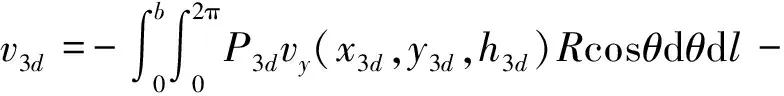
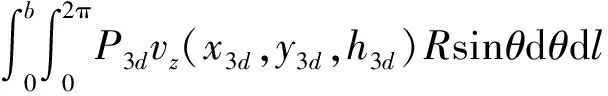
(29)

式中:P3u,P3d分别为上、下线的附加注浆压力。将其进行叠加,得到附加注浆力引起总的土体竖向和水平变形分别为

w3=w3u+w3d

(30)

v3=v3u+v3d

(31)

1.4.5 重叠盾构隧道土体变形总公式

叠加上文推导的土体损失以及3种因素引起的土体变形公式,得到最终的重叠隧道施工土体变形计算式,土体的竖向变形W和水平变形V计算式分别为

W=Uw+w1+w2+w3

(32)

V=Uv+v1+v2+v3

(33)

2 实例验证

将天津地铁五号线成林道站—津塘路站的重叠隧道区间[1]作为计算案例。该工程施工顺序为先下线、后上线,上、下线隧道的轴线埋深分别为15.1,26.1 m,盾构开挖直径为6.43 m,管片外部直径为6.2 m,监测区段隧道主要穿越粉质黏土层,上线隧道所在地层土体的剪切弹性模量Gu=6.5 MPa,泊松比μu=0.3,盾构机正面附加推力P1u=-20 kPa,盾壳摩擦力P2u=30 kPa,注浆压力P3u=60 kPa。下线隧道所在地层土体的剪切弹性模量Gd=7.5 MPa,泊松比μu=0.3,盾构机正面附加推力P1d=-20 kPa,盾壳摩擦力P2d=50 kPa,注浆压力P3d=80 kPa,盾构机长度L为8.5 m,注浆作用长度b为8 m。根据Matlab程序反分析得到:上线土体损失率ηu为0.53%,土体移动焦点参数βu为0.35,mu为2.3;下线土层土体损失率ηd为0.66%,βd为0.56,md为1.5。在实际工程中,后行线一般在土体沉降趋于稳定后开挖,因此上线开挖面与下线开挖面间距离K取-40 m。

先行线(下线)盾构隧道开挖时引起的纵向土体变形情况如图2所示,其中包含了笔者方法的计算结果以及其中各因素分别引起的土体变形。相比于只考虑土体损失的土体变形计算结果,考虑了多因素后求得的纵向沉降曲线与实测结果更吻合。

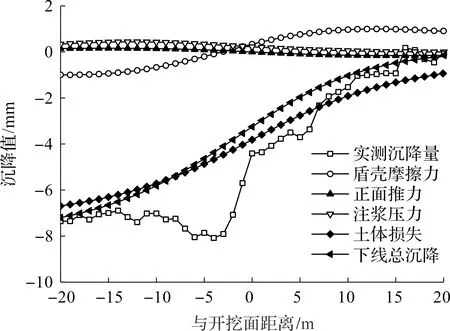
图2 先行线(下线)各因素引起的纵向地表变形

将横向土体变形监测数据与笔者方法的计算结果进行对比,结果如图3所示,其监测点距离下线隧道开挖面-20 m处。由图3可知:在考虑多因素的影响后土体的沉降槽要比只考虑土体损失时变得更宽,根据计算分析,主要原因是由于盾构机侧壁对土体作用的摩擦力引起土体扰动,导致了地表沉降槽宽度的增加。

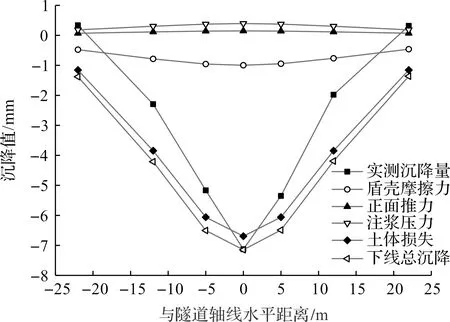
图3 先行线(下线)各因素引起的横向地表变形(xd=-20 m)

重叠盾构隧道引起的最终地表变形如图4所示,上下线开挖面的距离为40 m。由图4可知:先行线(下线)处引起的土体沉降已基本稳定,下线引起的最终沉降深度大致为7.5 mm;通过上下线相互叠加的方法求得的土体变形与实际监测数据较为吻合。重叠隧道施工阶段引起的横向土体变形如图5所示,该监测点距离后行线(上线)开挖面-20 m处。根据计算结果,此时盾壳摩擦力、注浆压力和正面推力对横向土体变形的影响并不明显,其原因可能是以上3种因素都发生于盾构机机身附近,对土体变形产生的作用会随着盾构机的推进而快速消散,此时监测点距离先行线开挖面有60 m,其影响已明显减弱,因此在双线隧道叠加后,土体损失在各因素中对土体变形影响的占比提高,导致土体损失产生的土体变形与总的沉降曲线极其接近。

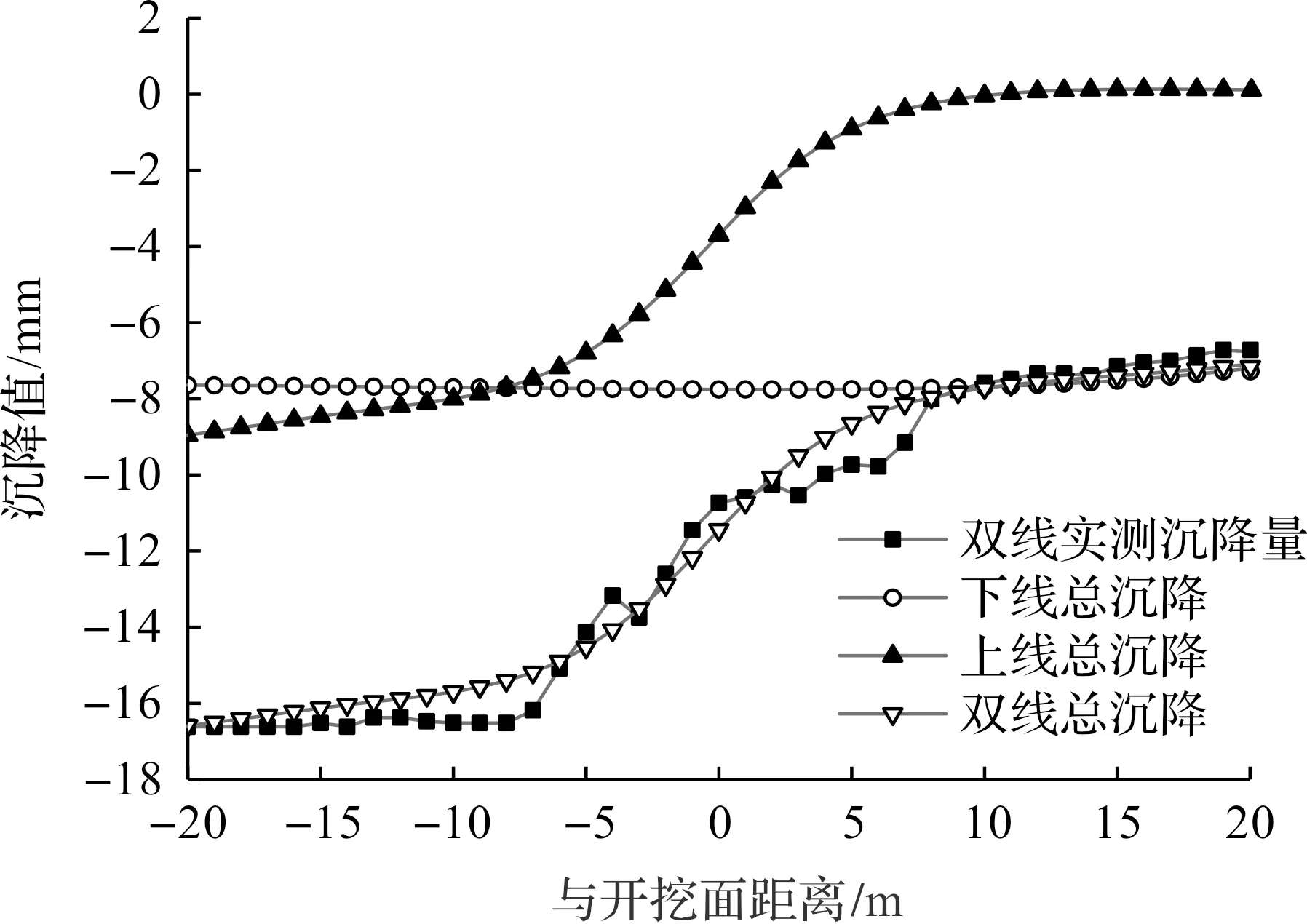
图4 重叠隧道引起的纵向地表总变形对比图

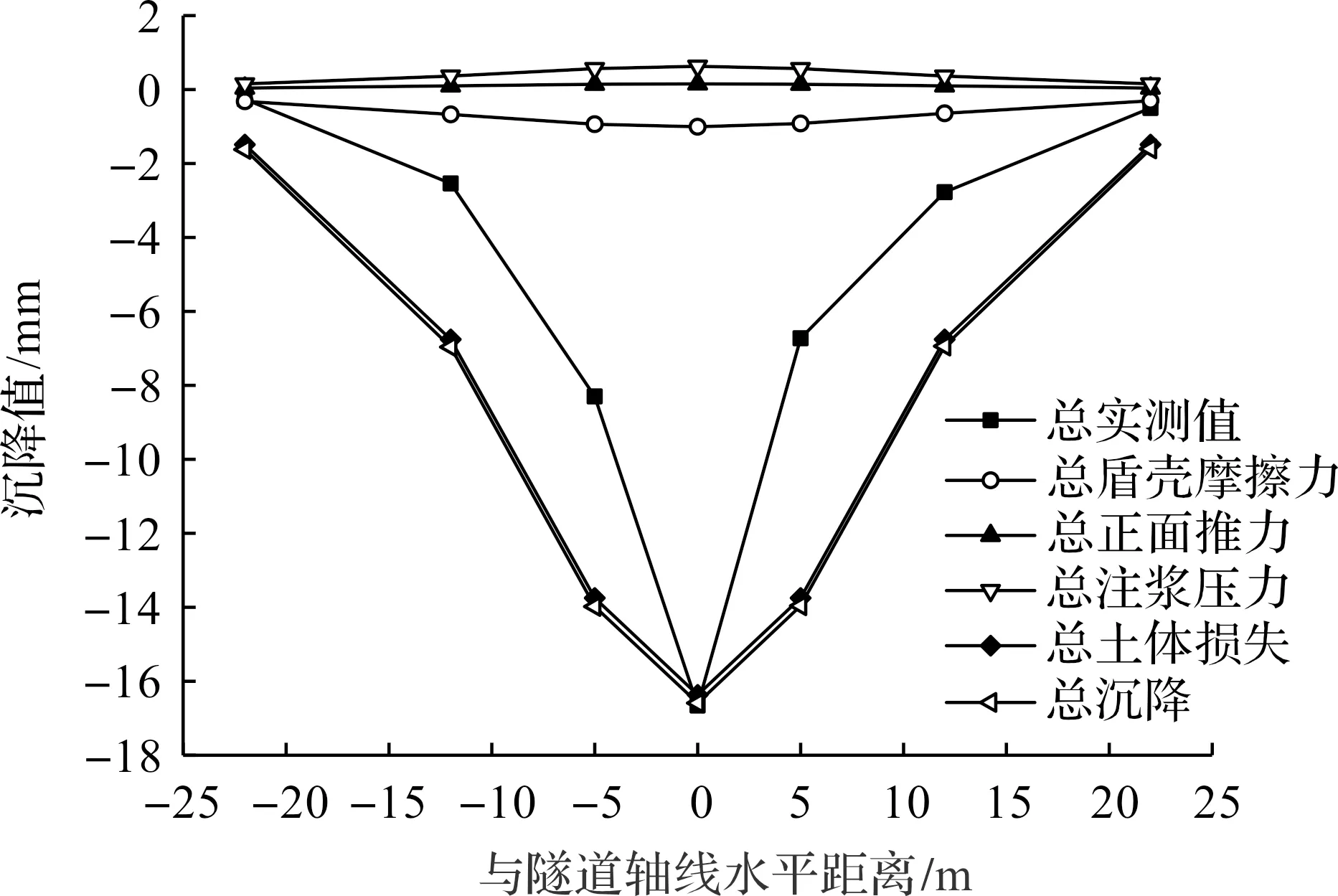
图5 重叠隧道各因素引起的横向地表总变形对比图(xu=-20 m)

与隧道轴线水平距离y=4 m处,不同深度土体的水平变形如图6所示,土体向轴线方向变形为负,反之为正。由图6可知:在上下线隧道附近土体的水平变形明显增大,随着土体深度超过下线隧道埋深,水平变形也逐渐趋近于0。土体损失导致的土体变形趋势与总的变形趋势基本相同且吻合度较高,由此说明与其他因素相比,土体损失是导致土体水平变形的主要因素。

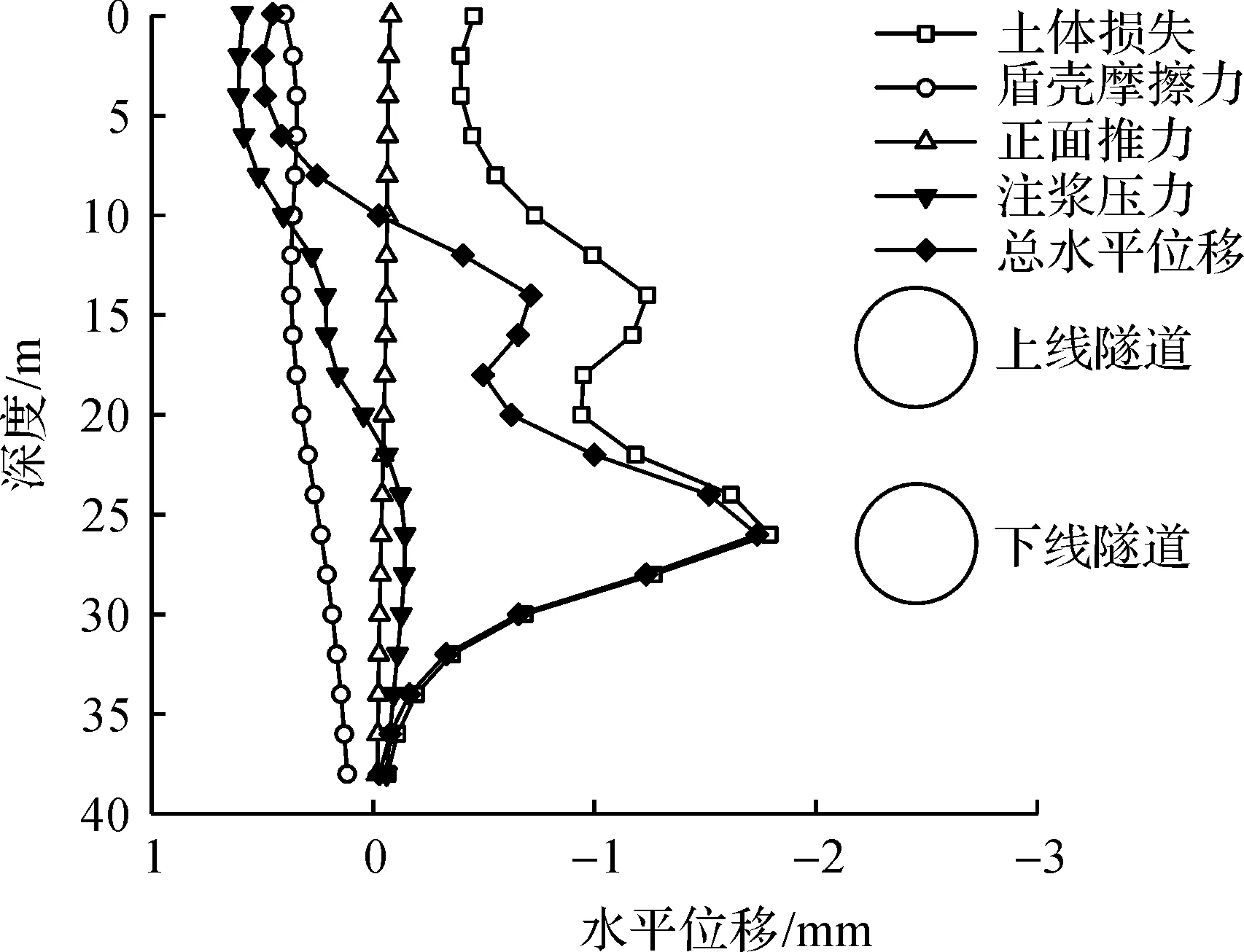
图6 重叠隧道各因素引起不同深度土体的水平变形曲线(xu=-20 m,y=4 m)

3 单因素分析

为检验修正后的三维统一解公式(3)相比原公式的优化程度,利用先行线(下线)的实测沉降量将修正公式和原式计算结果进行对比。修正公式中m为1.5,η与β取值与原公式中相同,分别为0.66%与0.56。对比结果如图7所示,修正后沉降曲线相较于修正前斜率更大且更贴近于实测值,证明修正后三维统一解公式对盾构施工引起土体变形的预测更为准确。

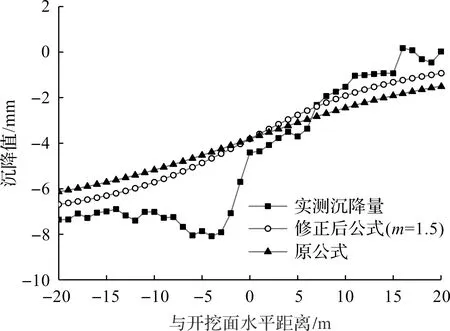
图7 统一解公式修正前后纵向地表变形计算对比图

采用单因素分析方法,当其他条件不变时,修正参数m的取值变化对纵向地表土体变形的影响如图8所示。根据计算结果发现:随着m值的增大,纵向土体变形曲线也随之变陡,趋于稳定所需的距离变短。然而m的取值不会改变土体的最大沉降量,这是因为最大沉降量由η决定,而m决定了沉降曲线趋于稳定的快慢。由此说明,修正后的三维统一解不仅可以适用于不同土质条件下的土体变形计算,而且能够提高与实测结果的吻合度。

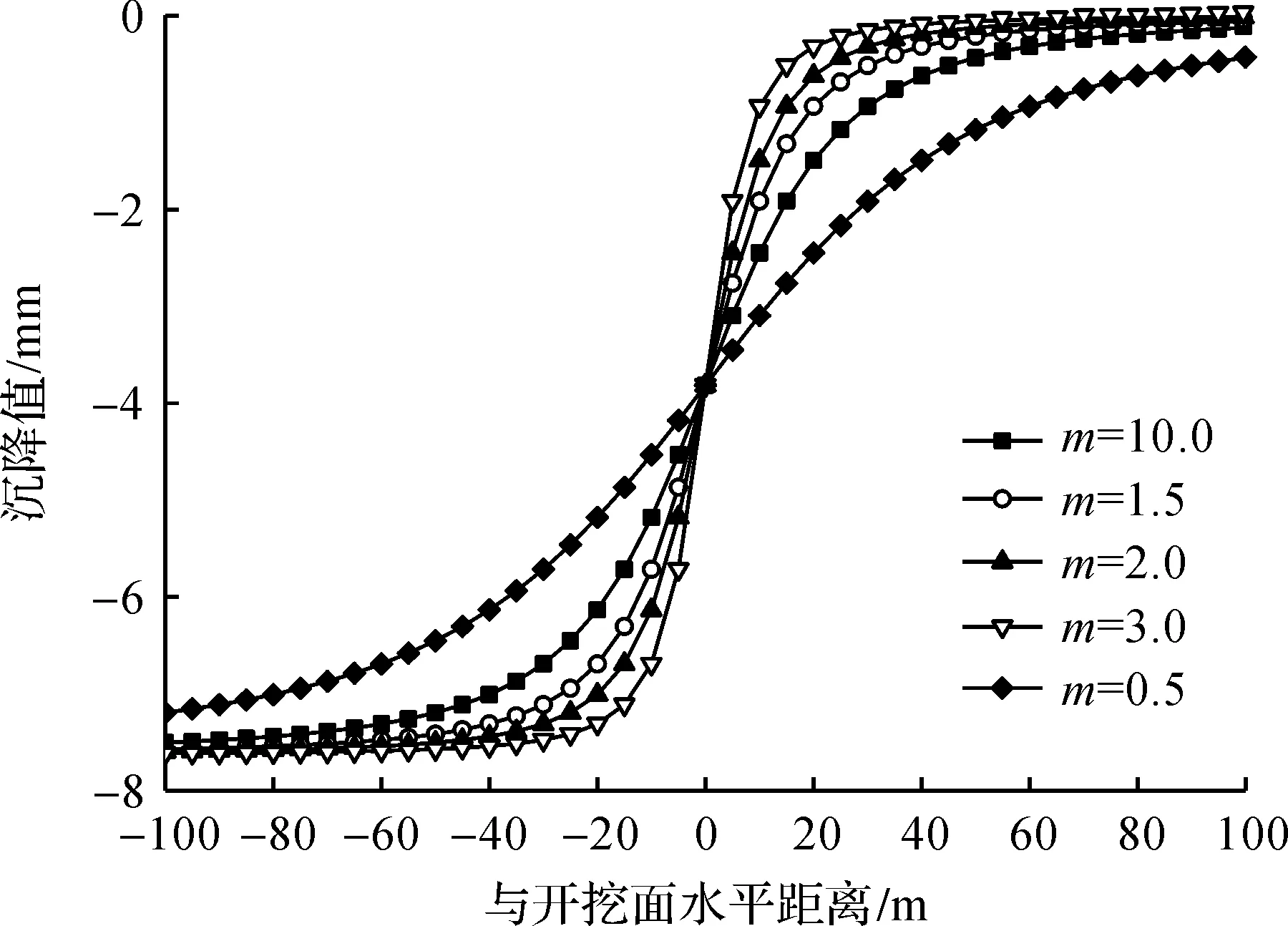
图8 参数m对纵向地表变形曲线的影响

4 结 论

在原三维统一解公式的基础上,加入考虑纵向土体条件的修正参数m,修正后的公式可充分考虑土体条件对盾构施工引起的纵向土体变形曲线的影响,土质越好,m值越小,反之越大。通过实际案例进行验算,证明了修正后的统一解公式对盾构施工引起的土体变形预测更为准确,适用的土质体条件也更为广泛。在修正后的三维统一解基础上,建立了考虑土体损失、正面附加推力、盾壳摩擦力和注浆压力4种因素共同作用下的重叠隧道施工引起的土体变形计算公式,计算方法适用于计算重叠隧道盾构施工中任意位置土体的竖向以及水平变形。结合工程案例,发现笔者方法相比于只考虑土体损失所得的结果与实测数据更加吻合,证明该方法的可行性。对于修正参数m的取值研究,后续需要进行大量工程数据的积累和反算才可对各区域和各类土体条件下的m取值范围进行确定。