高分辨率微线结构光测量系统设计

何娜，王建华，商执亿

（西安工业大学 机电工程学院，陕西 西安 710021）

引言

线结构光三维检测技术因其无损伤、高效、高精度等优势[1-3]，被广泛应用于工业及科学的各项领域[4-5]。智能制造的不断精密化及批量化对三维检测精度及效率提出更高要求[6]，线结构光测量技术朝高分辨、高精度、大视场方向发展。

常见的线结构光测量系统一般使用激光或LED 作为测量光源。2017年，李文涛等人采用激光视觉方法进行钢轨截面磨损动态测量，并提出一种结合相机自动曝光、动态阈值分割法和Hessian矩阵的激光光条中心亚像素提取方法，测量结果表明钢轨轮廓尺寸偏差约为0.01 mm[7]。2019 年GUO Xiaozhong 等人为快速获取齿轮齿面三维形状信息，提出一种基于线结构光传感器和高精度气浮转台的三维点云测量系统，利用该系统测量模数为3 的6 级齿轮，所得总齿廓偏差为15.87 μm[8]。2020年，WU Xiaojun 等人提出一种高精度相机标定及激光平面标定的三维激光扫描系统，通过测试不同试件得出该方法的最小几何测量精度为18 μm[9]。以上研究均以线激光作为测量光源，激光的高相干性导致测量条纹散斑噪声明显[10-11]，光条中心提取误差大，检测精度难以提高。

2012年，夏灵林等人改造光切显微镜搭建线结构光显微测量系统，该系统使用光切显微镜自带的非相干LED 绿光光源，投影条纹边缘平整，测量精度可达亚微米级，工作距离4.206 mm，测量深度范围±10 μm，成像视场183 μm[12]。以显微镜作为成像物镜可达到较高分辨率，易实现高精度测量，但由于其分辨率与景深参数相互制约[13]且放大倍率过高，因而往往伴随着小景深及小测量范围，使用远心镜头则可在保持高分辨率的同时有效拓展景深[14]，更易实现高精度、大范围测量。2021年，SHANG Z Y 等人提出一种非相干线结构光高精度轮廓测量方法，并搭建双远心测量系统，该系统可达到1.8 μm 的测量分辨力及1 mm 景深。将其应用于测量渐开线齿廓时，误差为±2.2 μm[15]，但该系统投影线宽较大，测量分辨力难以进一步提高[16]。

针对以上问题，本文提出高分辨率微线结构光测量系统，利用非相干性LED 投影宽度不足10 μm且边缘平整的光条，更易实现高分辨、高精度测量；利用高分辨率远心微距镜头搭建成像系统，在提高分辨率的同时增大物距，系统测量范围更大，应用范围更广。

1 微线结构光测量系统原理

1.1 系统组成

微线结构光测量系统分为投影光路与成像光路，投影光路包括光源、狭缝、投影物镜及其装夹微调装置等，其作用为进行光源光束整形从而产生主动测量[17]所需的原始投影条纹；成像光路主要由成像物镜、CCD 相机及其装夹微调装置等构成，用于拍摄投影于被测物表面且经被测物表面轮廓调制的信息条纹[18]，系统组成如图1所示。

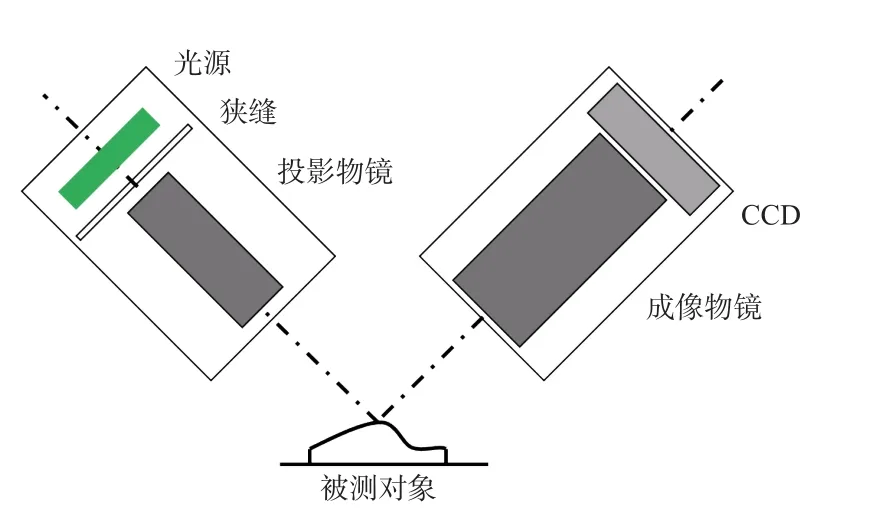
图1 系统组成Fig.1 Composition diagram of system

1.2 基本测量原理

线光源产生光束经狭缝光阑整形照亮狭缝轮廓，狭缝轮廓经投影物镜成像于被测物体表面，如图2(a)所示，此时被测物体表面呈现光条a-b-c-de-f，成像光路将物面的光条成于像平面即为信息光条a′-b′-c-′d′-e′-f′,最后由CCD 探测器采集并通过显示器显示出来[19-20]。被测物表面高度变化使得光条受到调制，表现在图像中则是光条发生了弯曲或断裂变形[21]，变形程度则取决于被测面深度[22]，因此从变形光条图像中可获取物体表面的三维信息。

图2 测量原理Fig.2 Diagram of measurement principle

设计要求测量系统既在深度方向具备相对较大的测量范围（0.15 mm），又拥有较高分辨率（约1 μm）。如图2(b)所示，当以投影光路光轴与成像光路光轴垂直且均与被测表面法线呈45 °夹角的方式搭建光路时，若将被测表面置于位置2处，则投影光条中心位于成像物镜的对准平面内，此时无论将被测表面位置移动至位置1 还是位置3，条纹1、条纹2、条纹3 的中心线对于成像物镜的物距是一致的，即无论被测表面如何起伏，光条中心总保持在成像物镜的对准平面内，成像物镜只需对条纹两侧能清晰成像，景深便足够。系统z方向测量范围主要取决于投影光路，与成像物镜景深无关。景深要求降低即可适当增加成像物镜数值孔径以满足最小分辨率要求。

1.3 深度标定模型

系统深度标定指对具有标准高度（深度）的工件表面进行条纹投影并拍摄图片，分析条纹图片得出CCD 单个像素对应的实际高度（深度）的过程。如图3 所示，在光路45 °投影、45 °拍摄条件下，利用标准量块高度差对测量系统进行深度标定，设量块高度差为Δh，CCD 像元尺寸为d，成像物镜放大倍率为β，量块高度差反映至像方尺寸为Δh′，其所占像素数为n，则系统单位像素深度D可由公式（1）得到，该式可用于后期系统深度标定的理论计算。

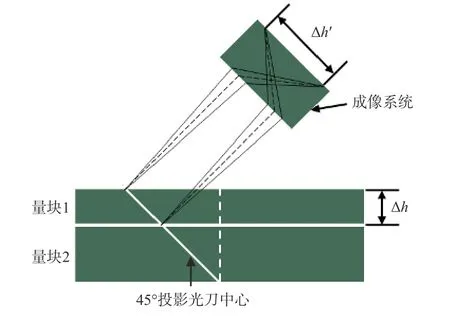
图3 深度标定理论模型Fig.3 Theoretical model of depth calibration

2 测量系统光路设计及搭建

2.1 光路设计

2.1.1 成像光路设计

系统以小模数齿轮为测量对象，需实现长度2 mm、宽度10 μm 的投影条纹，故成像物镜线视场y约2 mm。选用2/3″工业CCD（感光面宽度a为8.8 mm）相机作为成像接收器件，则可得成像镜头放大倍率β为

以显微成像且被测物体被其他光源斜照明为光路模型，则成像物镜理论最小分辨率 σ为

式中：λ为成像光主波长：NA为镜头数值孔径。当成像物镜的分辨率 σ为1 μm、λ为0.55 μm时，可反推出其数值孔径NA为0.275。

经过以上分析，选择数值孔径为0.2、放大倍率β为4.4 的远心微距镜头作为成像物镜，该镜头在0.55 μm 工作波长下的标称分辨率为1.68 μm，在光源斜照明条件下的理论分辨率 σ为1.375 μm，由此计算与该镜头适配的CCD 相机的像元尺寸d为

根据上述计算，选择像元尺寸为3.45 μm 的500万像素CCD 相机，此时CCD 像元尺寸3.45 μm 大于上文计算所得的镜头适配CCD 像元尺寸2.75 μm，成像系统成为光学受限系统[23]。

2.1.2 投影光路设计

投影光路设计采用主波长0.55 μm 的单色绿光LED 作为测量光源，搭配光强可调光源控制器，可根据被测表面质量调节光源强度，从而呈现最佳光条质量。定制宽度20 μm、长度8 mm 的高精度光学狭缝，利用狭缝夹持器进行固定，搭配狭缝微调装置可对狭缝倾角进行调节从而获得测量所需的理想条纹状态。投影物镜选用倒置工业显微镜，镜头标称TV 失真0.02%，数值孔径小，出光平行度高，放大倍率4倍，可将长度8 mm、宽度20 μm的狭缝缩小至长度2 mm、宽度10 μm 以内。

2.2 系统光路搭建

光路搭建如图4 所示，投影光路与成像光路光轴垂直且分别与工件装夹台背板法线呈45°夹角。投影光路由光源、高精度光学狭缝、狭缝夹持器与微调装置及投影物镜构成；成像光路由成像物镜及其微调装置、CCD 相机等构成。

图4 系统光路Fig.4 System optical path

3 系统性能分析

通过实验分析所搭建的微线结构光测量系统的各项性能，包括系统分辨力、深度测量范围及投影条纹的最小线宽及其边缘质量。

3.1 系统分辨力

成像系统分辨力包括成像光路分辨率和测量深度像素分辨率。

3.1.1 成像光路分辨率

成像光路分辨率检测使用USAF 1951 分辨率测试靶，以瑞利判据为理论依据，当目标元素明暗条纹的灰度对比度小于73.5%时[24]，认为该目标元素可被分辨。实验获得分辨率测试靶第7 组元素1 的灰度对比度随拍摄物距变化曲线如图5 所示。由数据结果可知，该图组中清晰度最高的图片位置读数为6.94 mm，该图片中第4～7 组元素图案及第7 组元素局部放大如图6 所示。

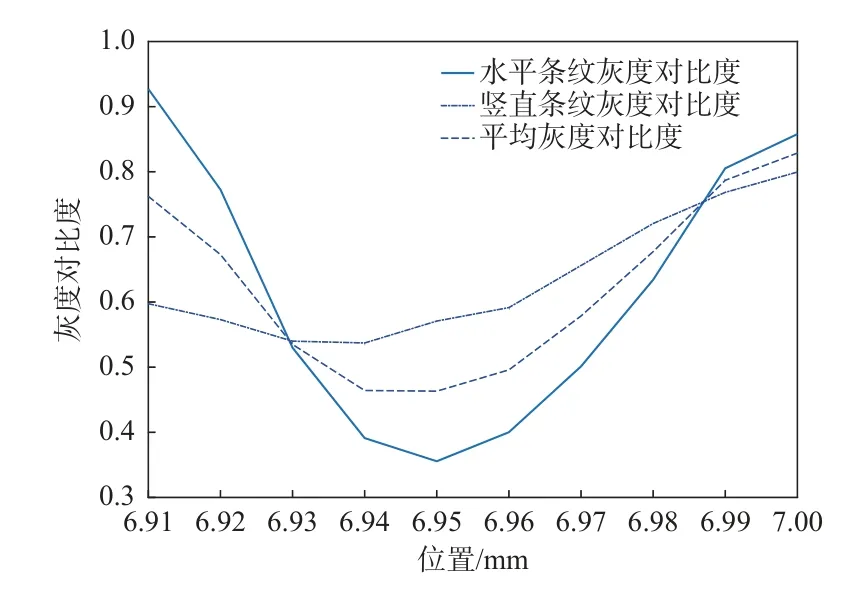
图5 第7 组元素1 灰度对比度随拍摄物距变化曲线Fig.5 Variation curves of gray contrast of group 7 element 1 with object distance

依次分析图6(b)中各元素灰度曲线，获得明暗条纹灰度极值，以灰度曲线上的灰度极小值与灰度极大值之比得各元素水平、竖直条纹对比度，即数据表1。结果表明，成像系统可分辨出分辨率靶第7 组最小元素，即其实际分辨率高于2.19 μm。使用最小二乘法对所得数据拟合直线得图7，由拟合直线可知，成像系统对竖直条纹的极限分辨率为1.616 μm，对于水平条纹极限分辨率及平均分辨率均超过1.616 μm，故可推论，成像光路极限分辨率可达到1.62 μm。

表1 第7 组各元素成像对比度数据表Table 1 Imaging contrast data for each element in group 7

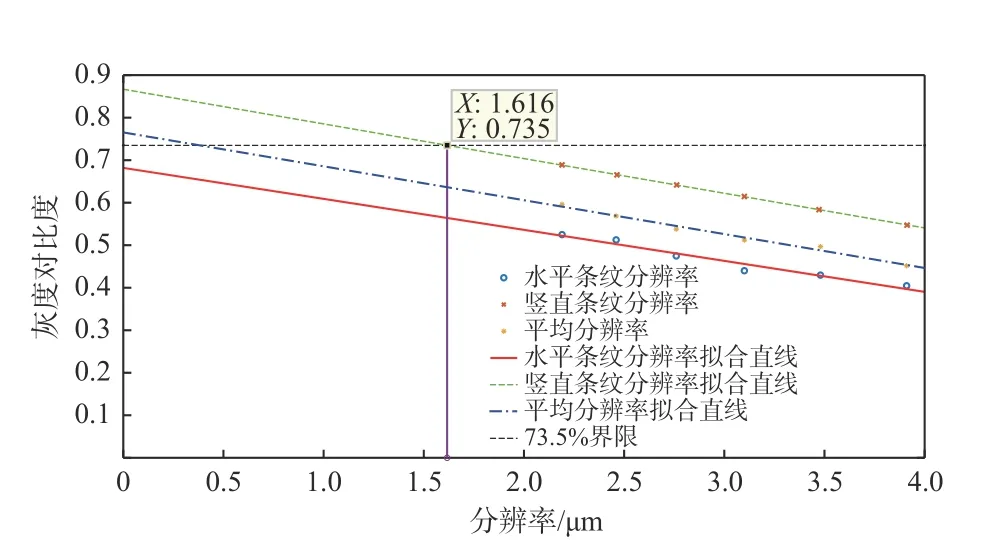
图7 第7 组各元素对比度拟合直线Fig.7 Contrast fitting line of each element in group 7

3.1.2 系统测量深度像素分辨率

上文已经获得系统深度标定的理论模型公式，带入本次实验所选用的CCD 像元尺寸3.45 μm 及成像物镜放大倍率4.4，可得系统测量深度方向的理论像素分辨率为0.554 4 μm。

通过实验测量实际所搭建光路在测量深度方向的像素分辨率，利用分子力将102 量块与05 量块黏合，并拍摄5 张位于视场不同区域包含量块高度差信息的条纹图像（图8）；使用自适应阈值分割算法提取条纹中心，最终计算得测量系统单位像素深度数据如表2 所示。

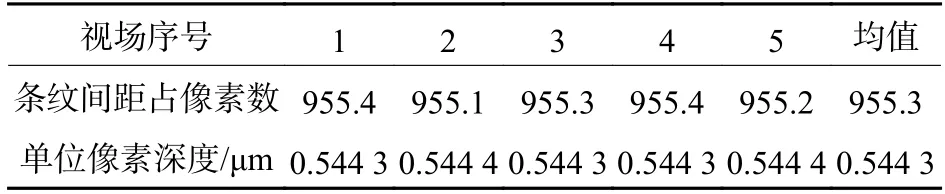
表2 CCD 单位像素深度计算数据表Table 2 Data of computed CCD unit pixel depth

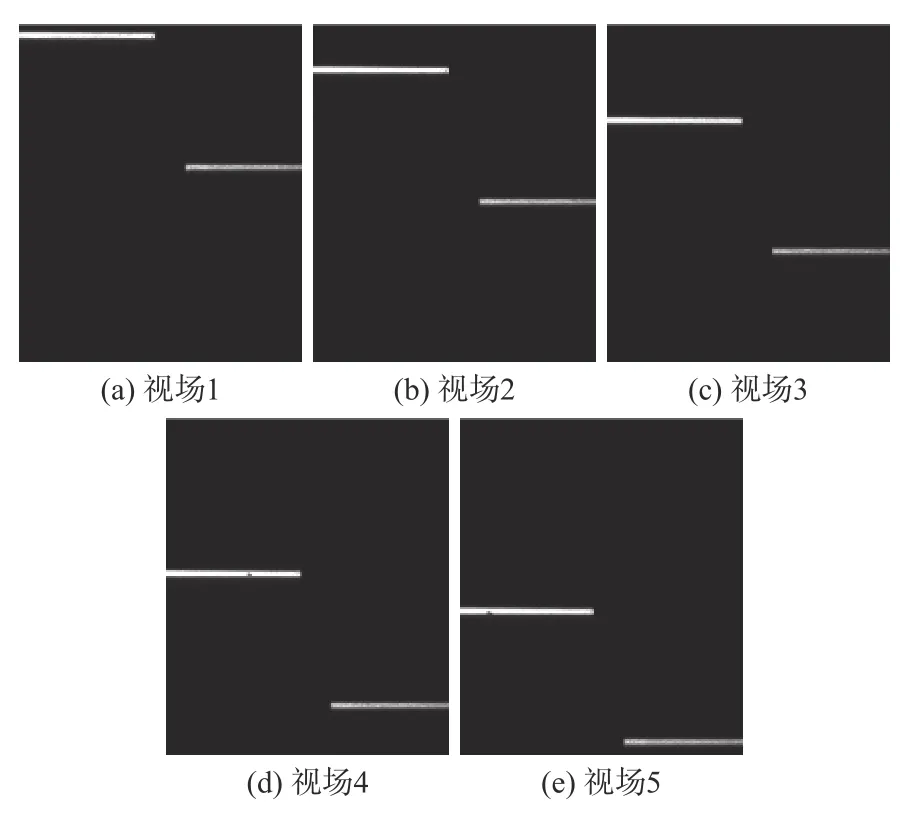
图8 视场不同区域拍摄包含高度差信息的条纹图Fig.8 Fringe patterns containing height difference information taken in different areas of field of view

由表2 数据计算得视场不同位置对应的单位像素深度均值为0.544 3 μm，即实际搭建光路在测量深度方向的像素分辨率为0.544 3 μm，与其理论值0.554 4 μm 接近。另外，在视场不同区域对520 μm深度进行测量，其所占像素数波动范围在0.3 像素以内，换算至物方对应0.17 μm，故可推论成像畸变对系统深度测量结果影响较小，由此计算镜头相对畸变约为0.032%，该值小于系统设计要求中给出的相对畸变0.05%，故搭建系统满足畸变设计要求。

3.2 系统深度测量范围

以光滑量块表面作为被测对象，等间距改变测量深度方向上量块被测面至系统的距离，依次采集条纹图像并计算其宽度变化率，如表3 所示。

表3 条纹宽度随投影距离变化情况Table 3 Variation of fringe width with projection distance

由表3 数据可知，在位置读数为10.70 mm～10.84 mm 范围内，投影条纹宽度相对于最细条纹宽度变化率不超过10%，这一位置差为0.14 mm，约等于投影物镜的景深0.135 mm，超过该范围后，条纹宽度增大趋势明显，如图9 所示，故可得系统深度测量范围为0.14 mm。

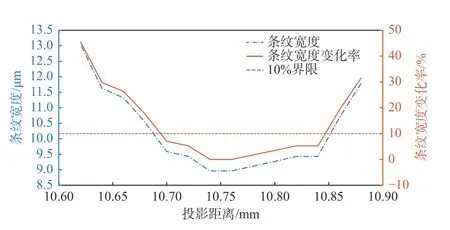
图9 条纹宽度及其变化率曲线Fig.9 Fringe width and its rate of change curve

3.3 投影光条宽度及其边缘质量

实验可知，被测物表面的细微瑕疵会使条纹边缘弥散，即条纹边缘灰度过渡范围变宽；较大蚀坑使得条纹边缘产生缺口甚至断裂。本次实验使用表面平整、光洁度高的金属量块作为被测表面，其显微拍摄图片如图10 所示。由3.2 节可知本次设计搭建的测量系统可投影的最小条纹宽度可达8.96 μm，其原始图像如图11(a)所示。由条纹区域放大图11(b)及区域放大灰度图11(c)可知，该被测表面所得条纹边缘较为平整，过渡清晰。条纹宽度及其边缘质量均符合设计要求。

图10 被测表面质量Fig.10 Surface quality of measured object

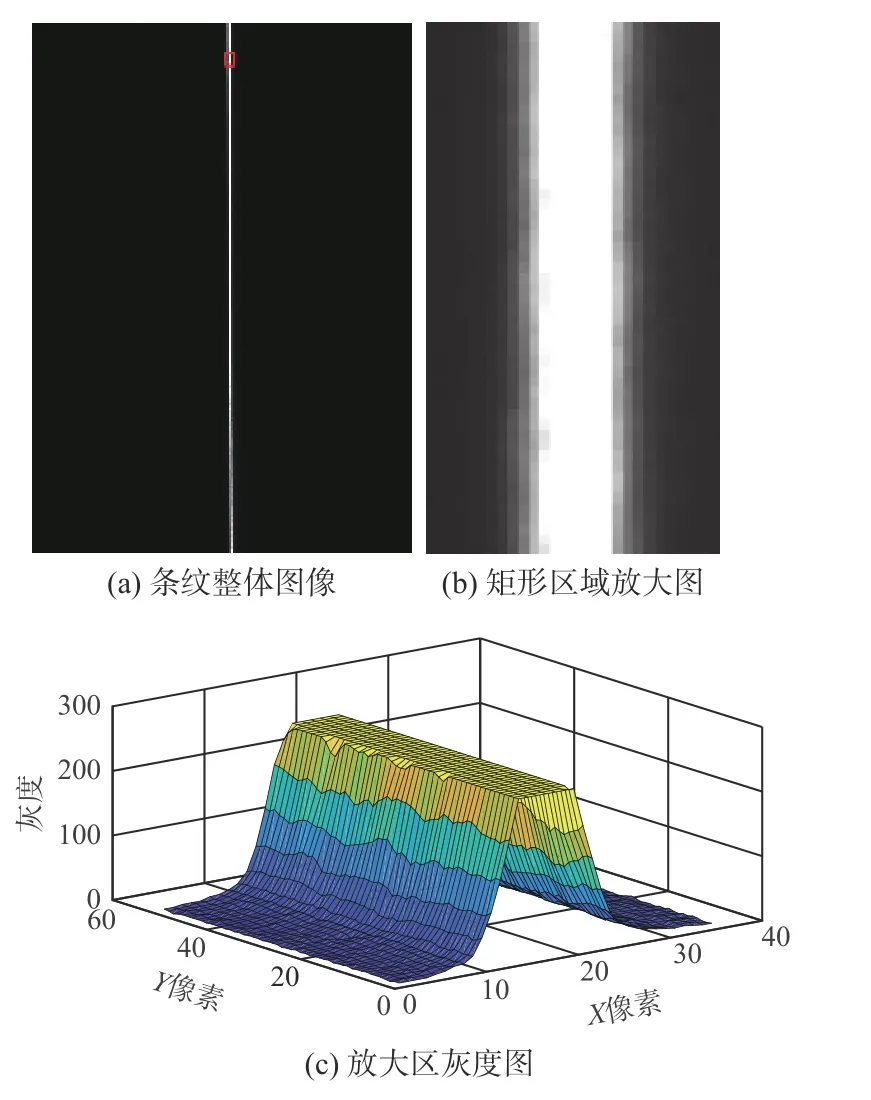
图11 宽度为8.96 μm 的条纹图Fig.11 Fringe pattern with width of 8.96 μm

4 结论

本文通过理论分析、设计并搭建高分辨率微线结构光测量系统。优化光路搭建方式，使得测量深度范围大幅提高。投影线宽小，更易实现高分辨、高精度测量。高分辨率远心微距镜头实现低畸变、大范围、大物距测量，大大改善了高倍显微镜仅能测量小薄工件的条件限制，应用范围更为广泛。实验结果表明，所搭建光学测量系统投影条纹长度1.5 mm，最小线宽可达8.96 μm，条纹边缘清晰、平滑；系统成像畸变极小，可实现1.62 μm的光学分辨率及0.54 μm 的深度像素分辨率，工作距离65 mm，深度测量范围不低于140 μm。下一步预计将所搭建微线结构光测量系统应用于小模数齿轮齿廓等微小物体表面轮廓测量中，从而确定其实际测量效果。