四象限探测器光斑检测原理及其研究进展

李征，许昊宇，梁静远，张颖，柯熙政,2,3

（1.西安理工大学 自动化与信息工程学院，陕西 西安 710048；2.西安文理学院 信息工程学院，陕西 西安 710065；3.陕西省智能协同网络军民共建重点实验室，陕西 西安 710048）

引言

在无线激光通信系统中，捕获、瞄准和跟踪（acquisition,pointing and tacking，APT）技术是一项研究的重点[1-3]，而光斑检测技术是APT 技术中的关键。光斑检测技术中常用的光斑探测器有位置敏感探测器（position sensitive detector，PSD）、电荷耦合器件（charge coupled device，CCD）、四象限探测器（quadrant detector，QD），相比于位置敏感探测器和电荷耦合器件，QD 具有检测分辨率高和响应时间短等优点[4-5]，因此被广泛应用。基于QD 的光斑位置检测技术已经广泛应用于激光雷达、激光测距和空间激光通信领域，使用QD 进行光斑位置检测时，其检测精度会受到各种因素的影响。光斑位置检测技术性能的好坏影响整个系统的性能，因此开展提高光斑位置检测精度的研究至关重要。基于QD 光斑位置检测模型算法是根据QD 的四路输出信号进行光斑的质心位置解算，学者们为了提高光斑位置检测范围和提高位置检测精度提出了不同的光斑检测算法，有加减算法、对角线算法、差比和算法、对数算法、函数拟合法、归一化中心法、多项式拟合法、无穷积分法、Boltzmann 函数拟合法、Composite 拟合算法和无穷积分改进算法。除了光斑检测算法外，光斑的形状和分布，探测器自身缺陷，环境因素和光、电噪声等因素也影响光斑位置检测精度。

综上所述，目前光斑位置检测技术的研究主要围绕光斑位置检测算法和影响光斑位置检测精度的因素开展。因此，本文介绍了光斑检测中涉及的几种常用光斑模型，然后围绕四象限探测器，从检测原理、国内外研究进展、影响因素、检测算法和应用等方面进行分析总结，并根据发展现状对光斑检测技术的应用及其发展前景进行了展望。

1 QD 光斑位置检测原理

四象限探测器是根据四象限探测器的四路输出信号进行光斑的质心位置解算，在目标定位、跟踪中应用广泛。为了能更好地运用四象限探测器，需要了解基本的光斑模型和检测原理。

1.1 光斑模型

输入的光斑模型不同，QD 的输出信号值也不同，所以讨论光斑模型有一定的意义。光斑模型按能量可分为均匀分布和高斯分布，按形状可分为圆形光斑、椭圆光斑和环形光斑。

如图1 所示，理想光斑为均匀分布的圆形光斑，其能量密度分布函数[6]为

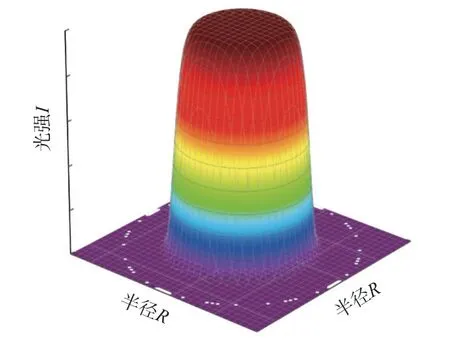
图1 均匀分布的圆形光斑Fig.1 Uniformly-distributed circular light spot

式中：I0为光强的均值；R为光斑的半径；光斑的中心坐标是(x0,y0)。

如图2 所示，激光器输出的光斑可看作高斯分布的圆形光斑，其能量密度分布函数为[7-8]

式中：I0为光强的峰值；R为圆形光斑的半径，光斑的中心坐标是(x0,y0)。

如图3 所示，为了减小实验误差，在实验分析中将接收到的光斑近似看为均匀分布的椭圆光斑，其能量密度分布函数为

图3 均匀分布的椭圆光斑Fig.3 Uniformly-distributed elliptical light spot

式中：I0为光强的峰值；wa、wb分别为椭圆光斑的长、短轴。

如图4 所示，当光斑漂移时，将被遮挡的光斑看为高斯分布的椭圆光斑，其能量密度分布函数为[9-10]

图4 高斯分布的椭圆光斑Fig.4 Gaussian-distributed elliptical light spot

式中：I0为光强的峰值；wa、wb分别为椭圆光斑的长、短轴。

在实际实验中，使用卡塞格林望远镜[11]接收光斑时副镜会使光斑中心受到遮挡，从而呈现环形光斑。如图5 所示为高斯分布的环形光斑，其能量密度分布函数为[12]

图5 高斯分布的环形光斑Fig.5 Gaussian-distributed ring light spots

式中：k为转换因子；R为外环光斑半径；S1为光斑内环圆的面积；S2为光斑外环圆的面积。

1.2 基于QD 的光斑位置检测原理

光斑检测技术中常用的光斑探测器有3种，分别是PSD、CCD 和QD。如表1 所示，为3 种探测器的对比。QD 相比CCD 和PSD，信号处理难度较大；但QD 体积小、响应速度快、位置分辨率高，在空间激光通信精跟踪系统中使用更具潜力。

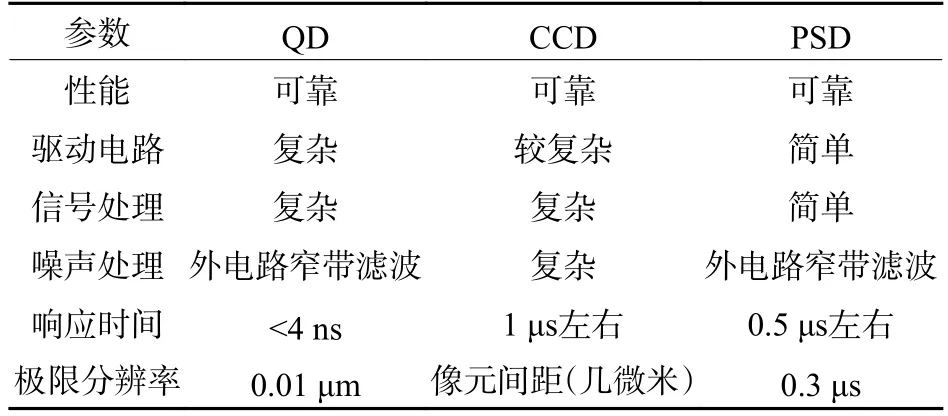
表1 三种探测器的对比[13]Table 1 Comparison of three detectors

QD 是一种光伏型半导体探测器件，如图6 所示为QD 示意图。它由4 个象限组成，每个象限都是1 个光电二极管或雪崩光电二极管安装在光敏面上。当光斑照射在QD 上时，通过4 个象限的输出电流对光斑中心进行定位[14]。

当激光光斑入射在QD 上时，4 个象限输出不同的光电流IA、IB、IC和ID，通过计算得到偏移量，从而实现光斑中心定位。用σx、σy表示归一化后的结果，假设光斑能量均匀分布，则光斑面积与光斑能量成正比，使用传统加减算法的计算公式为[15]

式中：EA、EB、EC和ED表示4 个象限的光斑总能量；SA、SB、SC和SD表示4 个象限的光斑面积。

2 基于四象限探测器的光斑位置检测

空间激光通信系统需要具有捕获、瞄准和跟踪（APT）系统，以保证通信两端实现精密对准与稳定跟踪。APT 系统的跟踪效果往往取决于光电探测器光斑位置检测的精度，QD 作为精密测向器件，更适合于动态目标的跟踪测量。

2.1 国外研究进展

基于QD 的光斑位置检测技术是APT 系统中的关键技术，光斑位置检测精度影响系统性能，因此开展光斑位置检测技术的研究至关重要。国外众多学者对QD 检测光斑进行了深入研究，其进展如下。

1985年，日本航天局研制了LUCE（laser utilizing communication equipment）系统[16]。LUCE 系统的APT子系统的精跟踪探测器和超前瞄准探测器都采用的是QD，精跟踪精度优于0.7 μrad。如图7 所示为LUCE 终端[17]的内部结构示意图。

图7 LUCE 终端的内部结构示意图[17]Fig.7 Schematic diagram of internal structure of LUCE terminal

1995年，日本邮电部实验室[18]用工程测试卫星VI 进行了卫星终端LCE（laser communication equipment）与地面站的激光通信试验,跟踪模块采用QD，精度可以达到2 μrad 以下。如图8 所示为LCE 的原理框图。

2001年，GUELMAN M 等人研发了宽带激光链路BLISL（broadband laser inter-satellite link）系统，采用QD 对光斑进行对准、跟踪[19]。如图9 所示为设计的BLISL 系统结构图。

2002年，TOYODA M 等人对光斑检测传感器进行了对比研究[20]，如图10 所示为激光跟踪系统。研究表明，在大于4 pW 的接收光功率下实现了小于1 μrad 的等效噪声角。

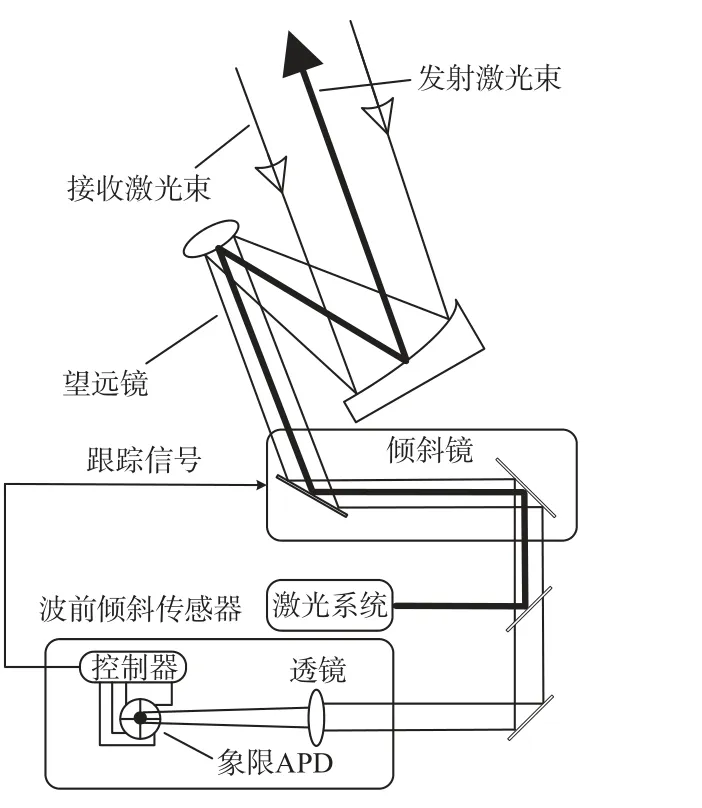
图10 基于象限APD 的激光跟踪系统示意图[20]Fig.10 Schematic diagram of laser tracking system based on quadrant APD

2006年，光学轨道间通信工程试验卫星与光学地面站终端KODEN[21]成功实现了星地双向通信试验，如图11 所示为KODEN 的接收机。该试验采用QD对光斑位置进行检测定位，其跟踪精度可达2 μrad。

图11 KODEN 接收机示意图[21]Fig.11 Schematic diagram of KODEN receiver

2009年，LEE E J 等人研究了入射光斑尺寸对四象限光电探测器的影响[22]。实验和分析研究表明，随着高斯光斑的减小，检测灵敏度增加。实验装置如图12 所示，通过改变光束扩展器的2 个透镜L1和L2之间的距离来改变光斑的大小。

图12 实验装置图[22]Fig.12 Schematic diagram of experimental device

2012年，SCHMIDT C 等人设计了一种小型激光终端SLT（small laser terminals），采用QD 作为光斑探测器件，最大通信距离为3 km，误码率为10-6[23]。如图13 所示为SLT 的基本框图。

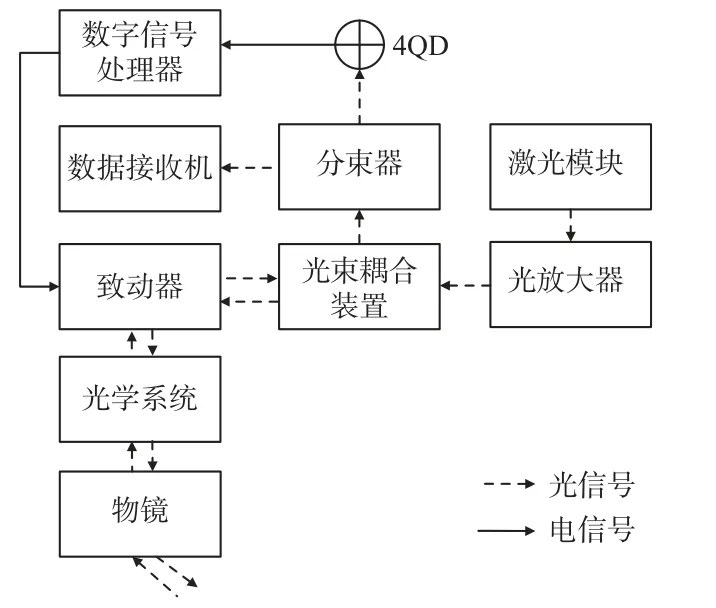
图13 SLT 的基本框图[23]Fig.13 Basic block diagram of SLT

2013年，BARBARIĆ Ž P 等人推导了QD 面积与位置的全新关系，并分析了激光跟踪器系统模型[24]。结果表明，全新关系信号处理可以将跟踪精度提高30%。同年，LADEE（lunar atmosphere and dust environment explorer）搭载着光通信终端LLST（lunar lasercom space terminal）与地面进行了双向激光通信试验，LLST 终端[25-27]的APT 子系统如图14所示。

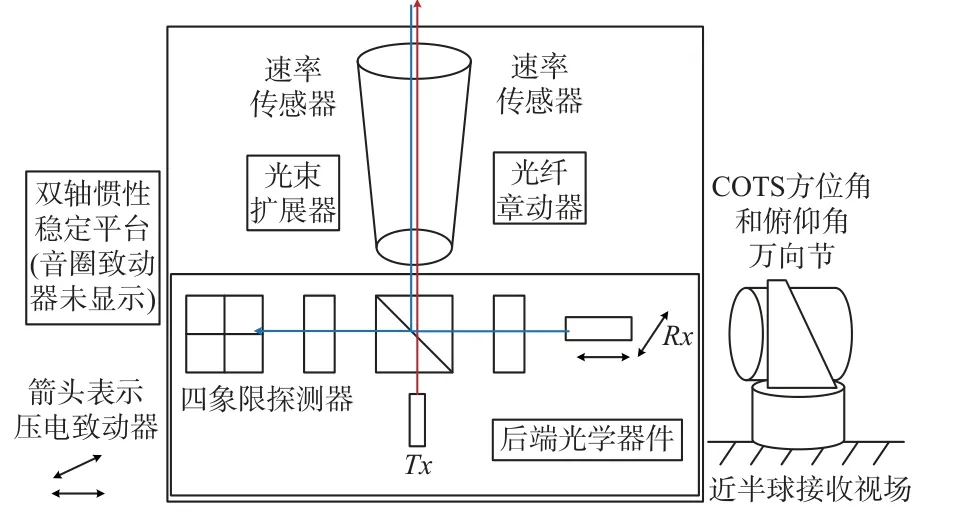
图14 LLST 光路图[28]Fig.14 Optical path diagram of LLST

2021年，SAFI H 等人研究了一种用于多旋翼悬停无人机的地对空自由空间光学链路，在光学接收机上使用1 个四象限的光电探测器阵列来探测光斑[29]。

2.2 国内研究现状

我国的研究学者在基于QD 的激光光斑位置检测技术方面也进行了深入的研究，如研究了影响光斑位置检测精度的因素，提出了不同的检测算法，并设计了不同的QD 光斑检测系统。

2.2.1 光斑位置检测精度影响因素研究现状

采用QD 检测光斑时，由于探测器自身的缺陷以及外部因素的影响，会对检测精度产生影响。因此，近年来我国研究学者对影响光斑位置检测精度的因素进行了如下研究。

2007年，徐代升研究了QD 误差信号与光斑位置、大小及探测器的关系，对引起因素进行了分析和定量估算[30]。2010年，赵馨等人研究了QD 的各种性能及外部环境对其性能的影响，并进行了实验测试[31]。2015年，张辉等人推导出高斯光斑模型下位置检测精度与光斑半径、质心位置和系统信噪比关系的数学模型[32]。2016年，张骏等人对背景光干扰、暗电流噪声、各象限光学效率及放大电路非均匀性等因素对QD 定位误差的影响进行了研究分析，并提出了相应的修正方法[33]。2017年，李世艳提出了一种光斑检测方法，判别光斑状态，并进行调节，提高了检测准确度[34]。2021年，李树德等人研究了各个噪声因素对采用QD 用于光斑位置定位的影响[35]。2022年，刁宽等人建立了光斑半径、能量分布和探测器死区等影响因素下QD 输出与光斑位置的表征方程[36]。表2 所示为光斑检测影响因素研究进展总结。

表2 光斑检测影响因素研究进展总结Table 2 Summary of research progress on influencing factors of spot detection

基于QD 的光斑检测精度和稳定性受到多种因素的影响，从上述研究进展可以发现，通过对影响因素进行优化，可以提高光斑检测系统的精度和稳定性，从而推动该领域的发展。不同因素对QD 光斑检测精度的影响将在第3 章进行叙述。

2.2.2 光斑检测算法研究现状

光斑检测算法的本质，是根据4 路光电流信号对光斑的质心位置进行解算。为了扩展检测范围和提高检测精度，我国研究学者对光斑检测算法进行了如下研究。

2009年，陈勇等人提出了将插值法和对角线算法相结合的一种改进算法[37]。2012年，司栋森等人提出了一种增益可调的快速跟踪定位（GAFT）算法[38]。2012年，陈梦苇等人对各种光斑模型讨论了和差、对角线、Δ/Σ 和对数4 种算法，并进行了比较[39]。2015年，WU J B 等人提出了Composite拟合算法，提高了测量精度[40]。2017年，郭小康等人简化了二段式多项式拟合算法，将检测精度提高到10-4mm 数量级[41]。2021年，苟晔鹏等人提出了一种基于无穷积分拟合方法的改进算法（GII）[42]。GII 算法的线性检测范围优于传统无穷积分拟合算法和8 次多项式拟合法，灵敏度高。2021年，秦立存等人改进了高斯光斑模型下的定位算法，提高了定位精度和线性范围[43]。表3 所示为光斑检测算法研究进展总结。

表3 光斑检测算法研究进展总结Table 3 Summary of research progress on spot detection algorithms

目前四象限探测器的光斑检测算法已经达到了很高的精度和准确性，但还存在一些问题，如环境噪声对测量结果的影响、光斑变形等。因此，在未来的研究中，我们需要进一步改进和优化现有的算法，并与其他相关技术相结合，以提高整个系统的性能和稳定性。光斑检测算法将在第4 章进行叙述。

2.2.3 光斑检测系统研究现状

我国研究学者对基于QD 的光斑检测系统进行了如下研究。2003年，王岱等人设计了双轴跟踪控制试验演示系统，能够快速捕获并平稳跟踪目标[44]。2013年，ZHANG W 等人研制了一种利用QD 做光斑检测探测器的小型激光跟踪系统[45]。2017年，范新坤等人提出了使用雪崩二极管型QD实现跟踪与通信复用的方案[46]。2018年，林鑫等人设计了一套基于QD 的激光束二维扫描跟踪系统，并进行了测试[47]。2019年，刘思鸣等人提出了一种基于QD 的激光跟踪系统[48]。2019年，王睿扬等人采用QD 作为通信接收机的探头，设计数字跟踪通信复合接收机[49]。2020年，王淋正等人提出了一种中心开孔型四象限探测器光纤定位技术，并设计了定位算法[50]。2021年，KE X Z 等人及梁韩立设计了一种基于步进电机和QD 的新型机载激光通信结构，实现光束的捕获、对准和跟踪[51-52]。2022年，陈韵等人设计了一套基于QD 与MEMS（micro-electro-mechanical system）振镜为伺服架构的微纳激光通信终端[53]。表4 所示为光斑检测系统研究进展总结。

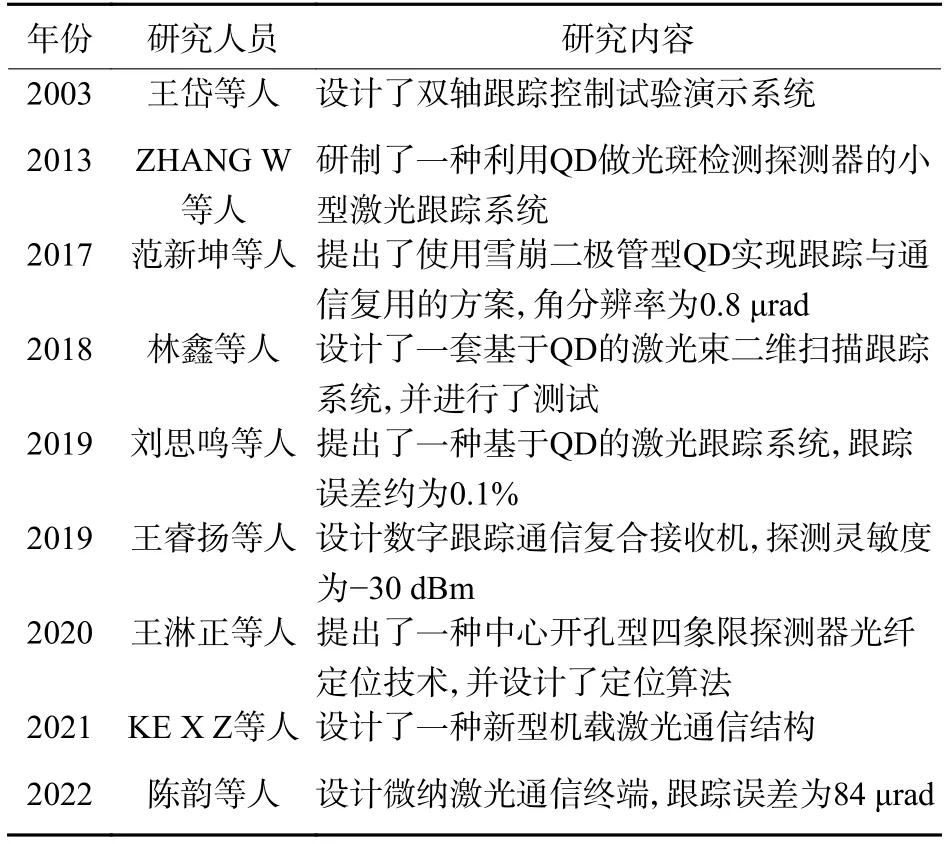
表4 光斑检测系统研究进展总结Table 4 Summary of research progress on spot detection systems

光斑检测系统主要是光束对准检测系统、QD的跟踪与通信复合系统和微纳激光通信系统等，将在第5 章进行叙述。

3 QD 光斑检测影响因素

影响光斑位置检测精度的因素有：光斑形状和分布，QD 自身缺陷，环境因素和光、电噪声，以及检测算法的影响。

3.1 不同模式光斑对QD 的输出影响

不同的光斑模式对QD 的输出是有影响的，一般研究的能量分布模型为均匀分布和高斯分布。对于高斯光斑，在x方向上QD 的输出与光斑移动距离关系可表示为[36]

如图15 所示，为不同光斑模式下光斑中心与QD 输出值的关系。均匀光斑的光斑位置检测灵敏度差，线性动态范围大；高斯光斑的光斑位置检测灵敏度高，线性动态范围小。

3.2 不同光斑半径对QD 的输出影响

假设光斑模型为均匀光斑，研究不同光斑半径下光斑中心与QD 输出值的关系，如图16 所示，光斑半径分别为r=1 mm、2 mm、3 mm。随着光斑半径的增大，QD 的检测灵敏度下降。

图16 不同光斑半径下的QD 输出值[36]Fig.16 QD output values under different spot radius

3.3 不同死区宽度对QD 的输出影响

QD 每相邻的2 个象限之间存在死区，死区的大小会影响探测器对光斑总能量的接收，从而影响光斑定位的精度。当死区宽度为d时，在x方向上，探测器的输出与光斑移动距离关系可表示为[36]

假设光斑半径为2 mm，死区宽度为0、0.04 mm、0.2 mm、0.3 mm时，如图17 所示，随着死区宽度增大，QD 的线性动态范围减小。

图17 不同死区宽度下的QD 输出值[36]Fig.17 QD output values under different deadband widths

3.4 不同背景光对QD 的输出影响

如图18 所示，为不同比例的背景光下光斑中心与QD 输出值的关系。随着背景光的增加，检测精度和灵敏度都在一定程度上降低。

背景光的存在会使QD 接收到的总能量增加，从而使输出电流增加。而通常情况下，环境光强可以认为是均匀的，因而也可认为背景光在QD 上各象限的分布是均匀的。因此，QD 在x方向上的输出信号与光斑移动距离关系可表示为[33]

式中：IA、IB、IC、ID代表各个象限产生的光电流；IBF代表整个QD 受背景光照射产生的光电流；IDK代表整个QD 的暗电流。

3.5 不同信噪比对QD 的输出影响

提高系统信噪比可以提高QD 的位置检测精度。光斑位置标准差受光斑半径、位置和系统信噪比3 个因素影响的关系为[28]

式中：RSNΣ为系统的总信噪比；r为光斑半径；x、y为光斑位置。

如图19 所示，随着信噪比增大，光斑位置标准差减小。

图19 不同系统信噪比下光斑位置标准差的变化曲线[28]Fig.19 Variation curve of standard deviation of spot position under different SNR

3.6 不同定位算法对QD 的输出影响

光斑质心检测算法是影响QD 检测精度的重要因素，常用的算法有加减算法、对角线算法、差比和算法和对数算法。假设光斑是均匀的圆形光斑，对4 种算法进行了对比，如图20 所示，可以看出，对于能量分布均匀的圆形光斑，4 种算法的线性度及灵敏度均有差异。差比和算法灵敏度上最优，线性范围最差；对角线算法虽有良好的线性，但低于差比和算法，灵敏度也有所下降；加减算法在灵敏度和线性范围上更为平衡；对数算法则有更宽的线性范围。

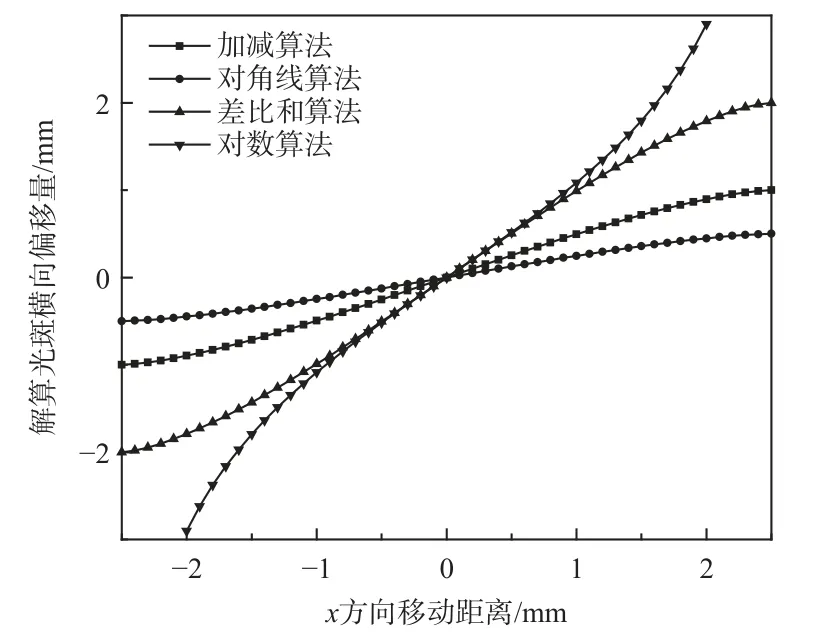
图20 不同定位算法下的仿真对比Fig.20 Simulation comparison under different positioning algorithms

3.7 各象限光学响应效率及放大电路非均匀性的影响

实际中由于制造工艺、半导体材料的掺杂水平、掩膜误差等情况的影响，输出值并不完全相等，会影响检测精度。而这种象限间的不均匀程度越大，探测器的定位精度也会随之减少。检测精度与各象限的电路增益和实际增益均匀度的表达式为[33]

式中：ρA、ρB、ρC、ρD分别表示各象限的光敏响应程度；IA、IB、IC、ID代表各个象限产生的光电流；AA、AB、AC、AD代表各个象限的电路增益。

如图21 所示，当光响应均匀度不一致时，对探测器线性范围的影响不大，但对检测精度有较大的影响，会降低探测器的定位精度。

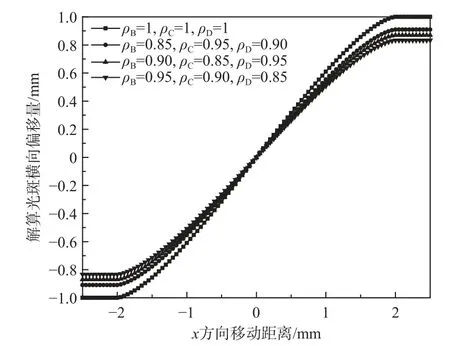
图21 各象限响应均匀度不同时对QD 输出的影响[33]Fig.21 Effect of different quadrant response uniformity on QD output

3.8 缺失光斑检测误差分析

将缺失光斑建模为理想的椭圆光斑，仿真分析光斑缺失对光斑检测的影响。圆形光斑和椭圆光斑在x、y轴方向上的偏移量Δx、Δy、ΔxT、ΔyT分别为

式中：P0为接收光功率；x0为x方向的移动距离；y0为y方向的移动距离；r为圆形光斑半径；wa为椭圆光斑长轴；wb为椭圆光斑短轴。

如图22 所示，为不同光斑模型下x、y轴偏移量分别随偏移检测值的变化曲线。可以发现，光斑变化越大，线性区间越小，缺失光斑会使QD 的可检测范围减小。

图22 不同光斑模型下X、Y 轴偏移量[34]Fig.22 Offset of X and Y axis under different spot models

总的来说，影响光斑位置检测精度的因素主要有：光斑形状和分布，QD 自身缺陷，环境因素和光、电噪声以及检测算法的影响。光斑形状复杂或者分布不均匀，会导致检测精度下降；QD 自身的缺陷会导致光斑位置的变化，从而影响检测精度，因此要尽量减少缺陷的产生；环境因素和光、电噪声会干扰检测，需要采用降噪技术来提高检测精度；检测算法的选择和优化直接影响光斑位置的检测精度。不同的算法具有不同的优缺点，需要根据光斑形状、分布和实际检测任务等因素进行选择和优化。因此，在进行光斑位置测量时，需要综合考虑以上因素，并尽可能采用可靠、精确的检测算法和技术，以提高光斑位置的检测精度。

4 光斑检测算法

采用QD 检测光斑位置时，根据探测器输出的四路信号来求解光斑质心位置。常用的算法有加减算法、对角线算法、差比和算法、对数算法、函数拟合法、归一化中心法、多项式拟合法、无穷积分法、Boltzmann 函数拟合法、Composite 拟合算法和无穷积分改进算法。

4.1 加减算法

当光斑照射到QD 上时，x、y轴偏移量与光斑面积成正比，用σx、σy分别表示光斑相对探测面中心的偏移，使用加减算法计算偏移量得[20]：

式中：UA、UB、UC和UD表示QD 中4 个象限的电压；SA、SB、SC、SD为QD 中4 个象限上的光斑面积。

4.2 对角线算法

为了扩展测量的线性区域，产生了对角线算法，在其线性区域内，光斑中心偏移量和光斑在探测器各象限面积成正比。使用对角线算法计算偏移量σx、σy得[20]：

4.3 差比和算法

对角线算法的测量灵敏度相较于加减算法有所降低，为提高测量灵敏度，提出差比和算法。在其线性区域内，光斑中心偏移量和光斑在探测器各象限面积成正比。使用差比和算法计算偏移量σx、σy得[20]：

4.4 对数算法

对数算法具有高带宽、宽动态范围和良好的线性，在其线性区域内，光斑中心偏移量和光斑在探测器上各象限面积成正比。使用对数算法计算偏移量σx、σy得[15]：

4.5 函数拟合法

函数拟合法[28]就是采用各种类型的函数对QD 的解算值与光斑中心实际位置关系拟合，解出光斑中心的位置，它们之间的关系曲线呈“S”型。

4.6 归一化中心法

归一化中心法是近似地将靠近QD 中心区域内的响应看作线性响应，用一阶函数来拟合得到光斑中心的实际位置[54]：

式中：k是比例系数，与QD 的形状大小、光斑强度分布以及死区宽度有关。

4.7 多项式拟合法

多项式拟合法采用高阶多项式对解算值与光斑实际位置之间的函数关系拟合[28]：

式中：an是拟合系数。

4.8 无穷积分法

无穷积分法是在假设QD 没有死区且无限大的情况下使用的，光斑中心的实际位置可表示为[54]

式中：r为光斑半径。

4.9 Boltzmann 函数拟合法

Boltzmann 函数拟合法是对解算值与光斑实际位置之间的函数关系拟合，函数表达式为[28]

式中：k是比例系数，与QD 的形状大小、光斑强度分布以及死区宽度有关。

4.10 Composite 拟合算法

Composite 拟合算法是通过将Boltzmann 函数拟合法和无穷拟合法两种算法线性融合的一种新的拟合算法，其光斑质心位置表示为[40]

式中：k1、k2是修正系数；m是权重；k1、k2、m可用N组实验或仿真数据按最小二乘法计算得到[40]。

4.11 无穷积分拟合改进算法

无穷积分拟合改进算法是在考虑QD 光敏面半径和死区宽度影响的情况下提出的一种算法，提高了定位精度。通过引入补偿因子，并采用分段多项式拟合方法对补偿函数进行拟合。光斑质心位置的表达式为[28]

如表5 所示，对四象限探测器常用的算法进行了总结。

表5 光斑检测算法总结Table 5 Summary of spot detection algorithms

随着科技的发展，四象限探测器光斑检测算法也不断发展和完善。算法的精度是影响光斑检测效果的关键因素，研究者通过改进算法，引入各种估计、优化等方法来提高光斑的检测精度。同时，研究者着眼于提高光斑检测算法的计算速度和实时性，以满足高速数据处理的需求。对于背景光的干扰，研究者从过滤、噪声预处理等方面入手，提高光斑检测的抗噪性和可靠性。研究者将自适应控制算法用于光斑检测，使其能够统一地适应各种信号噪声干扰情况，并为光斑检测提供更高效的处理方式。

随着QD 的不断进步，光斑检测算法也在不断地改进和完善，从精度、速度、适应性、抗干扰等方面提高了算法效果。

5 QD 光斑检测系统

基于QD 的光斑检测技术一方面应用于对待测目标进行线位移和角位移测量，另一方面应用于对待测目标或激光器发射端的动态跟踪。基于QD 的光斑检测系统有光束对准检测系统、基于QD 的跟踪与通信复合系统、微纳激光通信终端。

5.1 光束对准检测系统

如图23 所示，为光束对准检测系统结构。光学接收天线采用卡塞格林望远镜，在接收望远镜后放置检测模块，在分光棱镜的垂直方向放置圆筒状支架、调光镜头和QD。系统通过两台电机进行光束对准检测。

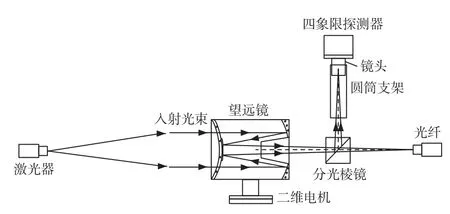
图23 光束对准检测系统结构[34]Fig.23 Structure diagram of beam-alignment detection system

5.1.1 缺失光斑检测测试

光斑通过捕获进入检测视场，如图24 所示为检测到的缺失光斑，检测结果表明，系统可以判别光斑状态。

图24 缺失光斑检测图[34]Fig.24 Missing spot detection image

5.1.2 系统对准测试

如图25 所示，为通过阈值检测算法将光斑调节至无缺失状态时检测到的完整光斑。如图26 所示，为光斑由缺失状态调节至完整光斑状态时探测器输出的结果。

图25 完整光斑检测图[34]Fig.25 Complete spot detection image

图26 调节过程QD 输出图[34]Fig.26 QD output diagram during adjustment process

5.2 QD 的跟踪与通信复合系统

QD 的跟踪与通信复合探测原理[46]如图27 所示，由激光调制发射单元、信号检测和处理单元、跟踪控制单元以及通信单元4 部分组成。

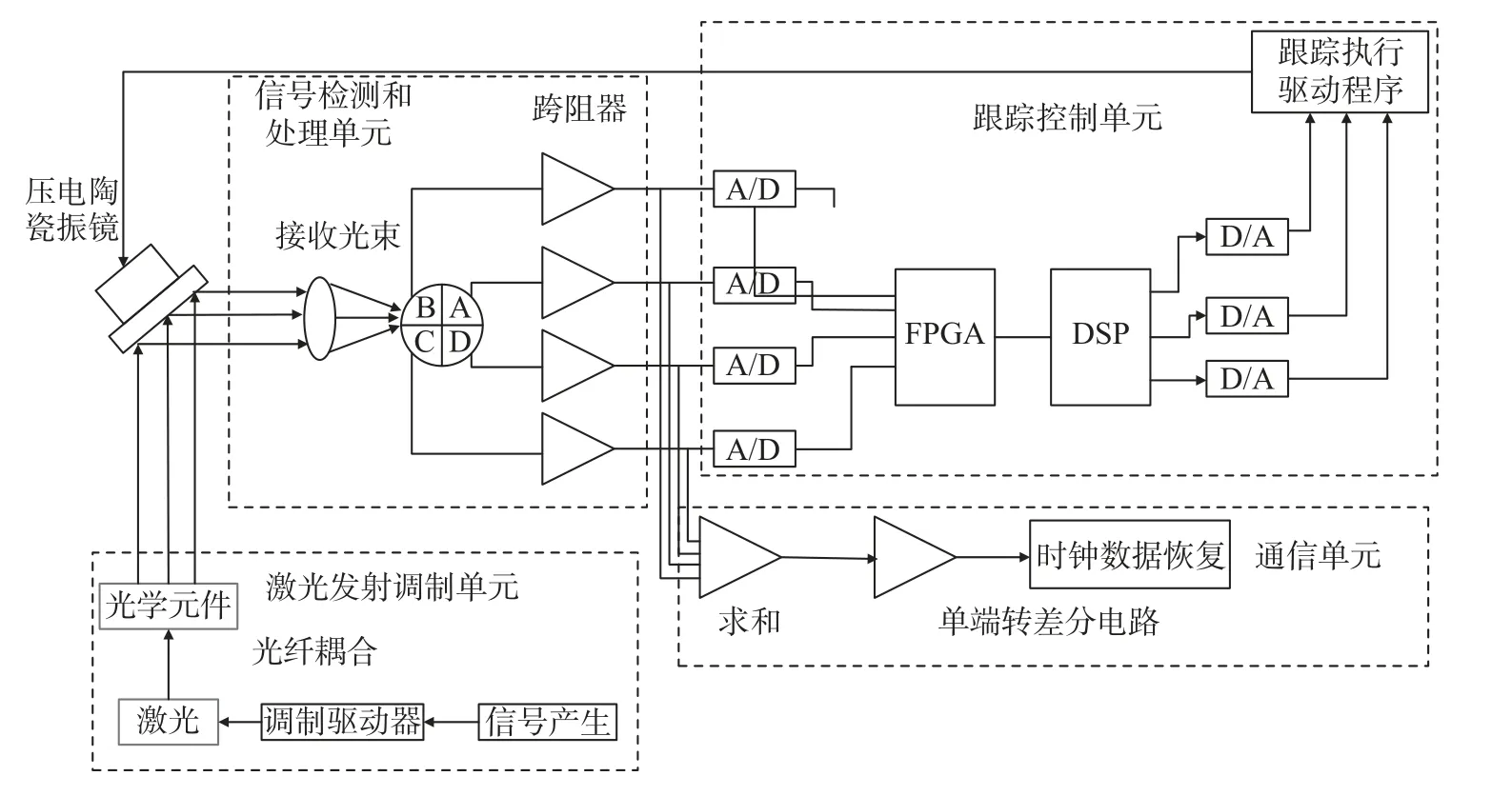
图27 跟踪与通信复合探测系统[46]Fig.27 Tracking and communication composite detection system

5.3 微纳激光通信终端

微纳激光通信终端[53]的光学架构与伺服系统结构如图28 所示。

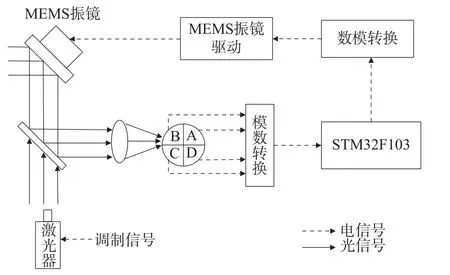
图28 微纳激光通信终端系统结构示意图[53]Fig.28 Structure diagram of micro nano laser communication terminal system

该系统结构由四象限探测器、MEMS 振镜、振镜驱动、模数转换、数模转换等单元组成，通过四象限探测器和MEMS 振镜完成对光斑进行跟踪。

6 光斑检测研究展望

本文以光斑检测为切入点，介绍了基本的光斑模型和QD 检测原理，综述了QD 检测光斑的发展现状，对QD 光斑检测影响因素和光斑检测算法进行了叙述，对QD 光斑检测系统进行了介绍。随着技术的发展，基于QD 的光斑检测研究也在不断深入和拓展。以下是一些未来研究的展望。

四象限探测器作为高精密器件，研究影响其检测精度的因素对提高光斑位置检测精度极其重要。随着制作工艺、材料质量的逐渐提高，死区和器件响应非均匀性的影响已经大大减少。因此，影响光斑位置检测精度的因素主要为光斑位置检测算法和光、电噪声，今后更多的研究可以集中于如何过滤和排除这些干扰因素。除了光斑的位置，光斑的形状对于光斑检测也非常重要，研究人员可以尝试开发能够同时检测光斑位置和光斑形状的技术。

不同的光斑检测算法具有不同的优缺点，传统的光斑检测算法无法兼顾灵敏度和线性范围，只适用于检测精度不高和线性范围不宽时的检测；函数拟合法的效果取决于算法采用的拟合函数，由归一化中心法发展到Composite 拟合算法，虽然其算法精度得到提高，却难以继续提升；多项式拟合法通过增加阶数来提升精度，但运算量也会随之提升。因此，需要提出一种检测精度高、运算量小的新型光斑位置检测算法，可以结合深度学习等现代技术，实现APT 系统中粗、精跟踪阶段的算法一体化。

总之，基于四象限探测器的光斑检测技术具有广泛的应用前景，未来研究可从提高精度、同时检测光斑位置和形状、结合深度学习等现代技术和多领域交叉相互融合等方向入手，为实现更多的应用场景和实际需求提供更好的支持和帮助。