基于傅里叶变换频谱分析的液体折射率实时测量系统

潘云，张建兵，周鹏，顾国庆

（1.南京航空航天大学金城学院，江苏 南京 211156；2.盐城市质量技术监督综合检验检测中心，江苏 盐城 224056；3.盐城工学院 土木工程学院，江苏 盐城 224051）

引言

折射率是透明或半透明材料的重要光学参数之一。对于液体的折射率，其大小与材料的物理、化学、生物等特性有关，因此对折射率的测量有利于进一步分析液体材料的特性参数，如液体的物质组成、生物医学标记和发酵动力学等[1-3]。在化工、生物制药、食品生产等工业实践和科学研究中，精确测定液体的折射率，特别是实时稳定的测量对于表征液体的特性和保证生产的质量有着重要的意义。近年来，对于液体折射率测量的方法主要有几何光学法[4,5]、波动光学法[6-8]、光纤传感法[9-12]和表面等离子体共振法[13-14]等。几何光学法主要是利用Snell 折射定律来测量折射率，其测量装置的结构通常简单易操作，常用于快速便捷测量。波动光学法主要是利用光的干涉和衍射现象，通过光程、偏振态、能量或波长的变化来实现折射率的测量，如迈克尔逊干涉仪[15]和马赫-曾德干涉仪[16]。周国全等基于等腰劈与矩形腔等倾干涉原理和CMOS（complementary metal-oxide-semiconductor）图像传感技术，实现了流体折射率微变的测量[17]。这些方法的优点是测量精度高，但是测量结果易受干涉系统的稳定性影响，不便于动态测量，一般多应用于实验室研究。光纤传感法和基于光纤的表面等离子体共振法均是利用光纤构造独特的干涉或衍射测量光路，如：光纤布拉格光栅（fiber Bragg grating，FBG）[18]、长周期光栅（long period fiber grating，LPFG）[19]和多芯光纤干涉仪等。光纤类测量手段有较高的灵敏度且制造成本低廉，但是对波长敏感，容易受到光源波动的影响。且由于光纤传感器的尖端浸在液体样品中，在测量一些特殊溶液时，可能会损坏光纤，样品也有可能被污染。

本文是在波动光学法的基础上设计了一款基于傅里叶变换频谱分析的便携式液体折射率实时测量系统。该系统利用劈尖等厚干涉原理来反映劈尖内液体折射率的变化，并通过CCD 相机记录等厚干涉条纹。为了克服传统波动光学测量方法的结构复杂、操作繁琐等缺陷，实现测量系统的可视化和小型化，本文基于树莓派（Raspberry Pi）平台，利用Python 编程语言搭建了对于干涉条纹图像的实时采集、处理和显示系统，通过傅里叶变换分析干涉条纹数量的变化来实现液体折射率的实时高精度测量。

1 等厚干涉法测量液体折射率

1.1 等厚干涉光路

波动光学法的稳定性和测量精度严重依赖光学系统的稳定性，为此本文设计了一款结构简单、稳定性高的共路劈尖等厚干涉系统。如图1 所示为基于劈尖等厚干涉光路的液体折射率实时测量系统示意图，小型半导体激光器（波长635 nm，输出功率5 mW）发出的激光经扩束准直系统后出射为一束平行光，并经分束镜1（透反比为1:1）反射后照射劈尖型液体容器。劈尖容器由透反比为1:1 的分束镜2 和倾斜角度可调的平面镜构成，分束镜2 将入射光分成两束，其中反射光直接照射到CCD 记录面上，作为参考光R；透射光穿过液体后被平面镜反射到CCD上，作为物光O与参考光R发生等厚干涉，干涉图像被CCD 实时采集。

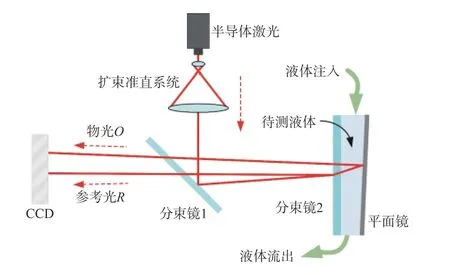
图1 液体折射率实时测量干涉光路示意图Fig.1 Interferometric optical path diagram for real-time measurement of liquid refractive index

1.2 测量基本原理

1.2.1 几何光学原理

图2 为图1 中平行光入射劈尖测量液体折射率的光路示意图，其中α和γ分别为入射光和出射光，即参考光R和物光O与分束镜2 法线方向的夹角；β和θ分别为劈尖的夹角以及物光O与参考光R间的夹角。

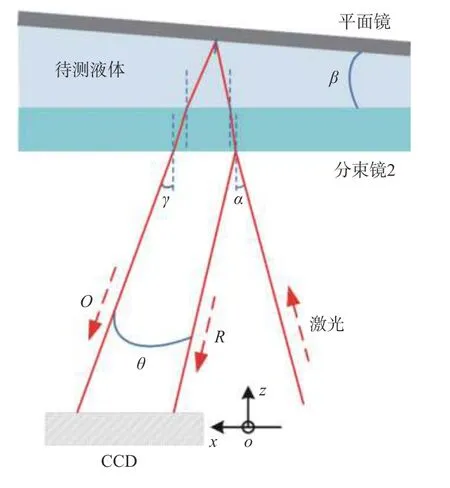
图2 劈尖等厚干涉测量光路示意图Fig.2 Optical path diagram of split-tip equal-thickness interferometry

根据Snell 折射定律，可以容易得出待测液体折射率n与入射角α、夹角β、出射角γ和空气折射率n0的关系为

同样可得，物光O与参考光R间的夹角θ可表示为

通过合理地设计分束镜1 的角度，使得经分束镜1 反射的平行光垂直入射分束镜2，即入射角α=0，则θ=γ，式（1）可简化为

1.2.2 干涉测量原理

基于上述分析，根据光的波动理论，在x-o-z平面内的物光O和参考光R入射到CCD 记录面上可分别表示为

式中：波矢k=2π/λ；AO和AR分别为物光和参考光的振幅；φO0和φR0分别为物光和参考光的初始相位，在后续分析中可以忽略。因此，物光和参考光在CCD 记录面上干涉产生的等厚干涉条纹的强度分布为

对式（6）进行二维快速傅里叶变换，可得干涉条纹的频谱分布为

式中：F[·]表示二维快速傅里叶变换；G0为零频直流分量；G+1和G-1分别为±1 级共轭分量。

根据式（4）～式（6），利用Matlab 软件模拟上述劈尖产生的等厚干涉条纹。为了与实际测量相符，设计了CCD 窗口（512 pixel×512 pixel）上记录的条纹数为非整数条（7.5 条），并且加入了大量椒盐噪声和散斑噪声，如图3（a）所示。利用二维快速傅里叶变换将条纹图像变换至频域，如图3（b）所示，频谱图中的3 个分量分别对应式（7）中的零频直流分量和±1 级共轭分量。

图3 基于傅里叶变换的仿真干涉条纹频谱分析结果Fig.3 Spectral analysis results of simulated interference fringes based on Fourier transform

根据±1 级频谱的坐标与窗口内等厚干涉条纹数N的关系，有：

式中：Lx为CCD 窗口的宽度。容易得出，在滤除其零频分量后，可以通过提取频谱中极大值分量的像素坐标来获取干涉条纹的数量、宽度等信息。但是，直接从图3（b）中提取±1 级频谱的像素坐标来计算条纹数为257-249=8条，与实际仿真的7.5 条不符。这是因为在实际测量中记录到的干涉条纹数往往为非整数条且包含大量噪声，因此为了提高±1 级频谱像素坐标的定位精度，如图3（c）所示采用了三次样条插值算法来拟合频谱采样不足的缺陷，插值后计算条纹数为257-249.4=7.6 条。最后，若劈尖的夹角β已知，那么根据式（3）和式（8）即可计算出液体的折射率为

2 基于树莓派的测量系统设计

为了实现整个测量系统的小型化，本文采用了树莓派（Raspberry Pi）作为最小系统来实现对液体折射率实时测量。树莓派的特点是程序编译简单、运算速度快、成本低、接口丰富、尺寸小，具备了普通计算机所有的基本功能，因此能很好地满足对干涉图像的高速采集、处理和同步显示的需求。

2.1 硬件装置设计

如图4 所示为整机装配示意图及其实物图，本文选用了Raspberry Pi 4B 4GB 版本作为运算处理平台，通过高速USB 3.0 接口连接CCD 相机（型号CGU2-500C-UVC，像素尺寸768 pixel×1 024 pixel，像元尺寸4.4 μm，采样频率30 帧/s）实时采集干涉条纹图像，然后经过运算处理后通过Micro HDMI高清视频输出接口将干涉图像、频谱图像和计算结果显示在3.5 寸的电容屏上。

图4 整机装配示意图及实物照片Fig.4 Assembly diagram and its physical image

图4（a）中白色椭圆虚线框所示为劈尖形液体容器的透视放大图，其中待测液体从上方注入然后从出水口排出。平面镜通过弹簧和调节螺丝固定在背板上，并且可以通过拧动螺丝来调节平面镜的倾角从而改变等厚干涉条纹的疏密和方向。为了保证光学系统的稳定性，如图4（b）所示，所有光学元器件均采用碳纤维板搭建的框架结构固定在一块5 mm厚碳纤维板底座上。整个树莓派系统、光学系统和内置5 V 电源均安装在3D 打印的黑色材料外壳内，从而可提升整体系统的紧凑性和便携性。

2.2 软件系统设计

整个系统的软件算法部分是以Python 编程语言为平台，搭建在树莓派的Linux 系统上。Python作为一种面向对象的编程语言，可以很方便地通过调用OpenCV 和numpy 等库函数实现CCD 相机的图像读取、数值处理以及图形交互的功能，具体程序流程如图5 所示。此外，为了提升整个系统的可视性和交互性，本文还基于3.5 寸（7/60 m）电容触摸屏设计了GUI 图形操作界面。

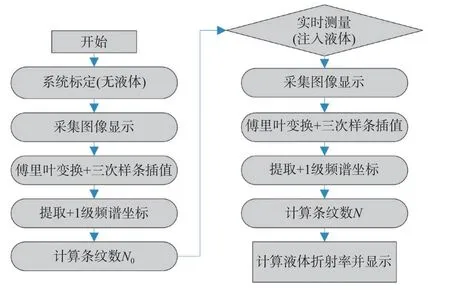
图5 液体折射率测量流程图Fig.5 Flow chart of liquid refractive index measurement program

由式（9）可知，对于液体折射率的测量需已知劈尖夹角和入射激光波长等系统参数，因此需要在实际测量前对光学系统的初始参数进行标定。即在未注入液体时，测定劈尖产生的等厚干涉条纹数N0，则式（9）可表示为

随后注入待测液体，CCD 相机实时采集干涉条纹图像并计算出干涉条纹数N，则可计算出实时液体折射率n为

由此可见，该系统只需测定液体注入前后的等厚干涉条纹数即可实现液体折射率的实时测量，而无需知道光学系统中劈尖夹角、入射波长等系统参数，减小了系统误差的产生。

3 实验结果与讨论

实验中，利用上述系统分别连续测量了室温下纯净水、无水乙醇和异丙醇的折射率，如图6（a）～图6（c）所示。对于常温下纯水的折射率1.333 0、无水乙醇折射率1.361 1 和异丙醇折射率1.377 2，其相对误差分别为0.48%、0.27%和0.11%。

图6 液体折射率测量结果Fig.6 Measurement results of liquid refractive indices

根据式（10）和式（11）分析可知，该液体折射率测量系统的测量精度和稳定性取决于两方面：一是激光光源的稳定性；二是干涉条纹的测量精度和稳定性。首先考虑激光器输出波长随温度变化的漂移特性，根据文献[20]中提供的半导体激光器典型温度漂移系数0.24 nm/℃，若激光器升高10 ℃将导致由式（11）计算的测量结果产生-0.376%的相对误差。但是，由于本系统中所使用的是小功率（5 mW）半导体激光器，实际测量过程中发热并不明显，因此可以忽略激光器温漂特性的影响。

其次，为了分析干涉条纹的测量精度和稳定性对测量结果的影响，分别研究了不同初始条纹数N0下，该系统通过测量流动纯净水的实时折射率来分析测量系统的时间稳定性。结果如图7（a）所示，初始条纹数越大，即等厚干涉条纹的宽度越小，测量系统的时间稳定性越高。这点也可以从式（3）和式（8）中推导出，干涉条纹的宽度与劈尖的夹角β成反比关系，因此夹角β越小，劈尖形液体容器产生的等厚干涉条纹的宽度越容易受到外界震动的影响。图7（b）给出了图7（a）中不同初始条纹数下测量纯净水的平均折射率（mean refractive index，MRI）、相对误差（relative error，RE）和标准偏差（standard deviation，SD）。结果进一步表明，上述测量系统在不同条纹宽度下均能很好地测量流动液体的实时折射率，最小相对误差为0.015%，最大相对误差为0.754%。

图7 不同初始条纹数下测量系统的时间稳定性Fig.7 Time stability of measurement system at different initial fringe numbers

标准偏差随着条纹的变宽逐渐增加，这表明在干涉条纹较宽（初始条纹数为26.7 条）时，系统的时间稳定性显著降低；当初始条纹数大于180 条时，测量系统均表现出较好的时间稳定性。因此，在满足Nyquist 采样条件的基础上，可以通过调节劈尖夹角来获得较大的初始条纹数，从而提高测量系统的时间稳定性。此外，通过观察图7（a）给出的长时间测量数据的水平稳定性，可进一步表明，激光器的温漂特性对本实验系统测量结果的影响可以忽略。

4 结论

本文在劈尖等厚干涉测量的基础上，设计了一种基于傅里叶变换频谱分析技术的液体折射率实时干涉测量系统。利用树莓派硬件系统中搭建的图像处理算法，可以实时记录等厚干涉条纹图像，并通过傅里叶变换提取其±1 级频谱图像，进而利用三次样条插值算法实现干涉条纹数的精确提取。整个测量过程只需提前标定未注入液体时劈尖产生的初始干涉条纹数，即可实现液体折射率的实时测量。实验中对不同液体折射率测量的相对误差均小于0.754%，且当初始条纹数大于180条时，测量系统具有很好的时间稳定性。再结合设计的GUI 图形操作界面，整个测量系统操作简单、直观可视、结果精确、小巧便携，适用于各种复杂环境中对液体折射率实时测量的需求。