基于GA-BP 神经网络的温室温度预测研究

李其操， 董自健

（江苏海洋大学电子工程学院， 江苏 连云港 222005）

0 引 言

中国是排在世界前列的农业生产大国，温室的面积占据着世界首位。 温室内的环境因素对于作物的生长有着至关重要的影响［1-2］。 目前，温室的调控方式大多是凭借工人的生产经验，通过获得的传感器数据，进行预判性的调控。 因此，能够精准的预测出温室内的温度情况，对温室调控系统有很大的帮助。

近年来，许多学者提出了针对温度预测的方法。如：左志宇［3］提出采用时序分析法建立温度预测模型的方法；徐意［4］构建了基于RBF 神经网络的温室温度预测模型；徐宇［5］构建了基于复数神经网络的温室温度预测模型；王红君［6］利用贝叶斯正则化算法对BP 神经网络进行改进，降低了影响温度的因子之间的耦合度等。

但是，上述预测模型都容易出现陷入局部最优的情况。 因此，本文利用遗传算法，对BP 神经网络的初始权值和阈值进行优化，使预测模型避免出现局部最优的情况，从而对温室内温度进行更精准的预测。

1 GA-BP 神经网络预测模型的构建

1.1 BP 神经网络

BP 神经网络的主要思想是：训练数据通过前馈网络训练后得到输出数据，将输出数据与期望数据进行对比得到误差，反向传播网络将得到的误差反向输入输出层，对网络的连接权值和阈值进行反复训练，缩小网络输出和期望输出之间的误差。

输入、输出层为单层结构，而隐藏层可以是单层或多层。 输入层、隐藏层、输出层之间的神经元都是相互连接的，为全连接。 BP 神经网络结构如图1所示。

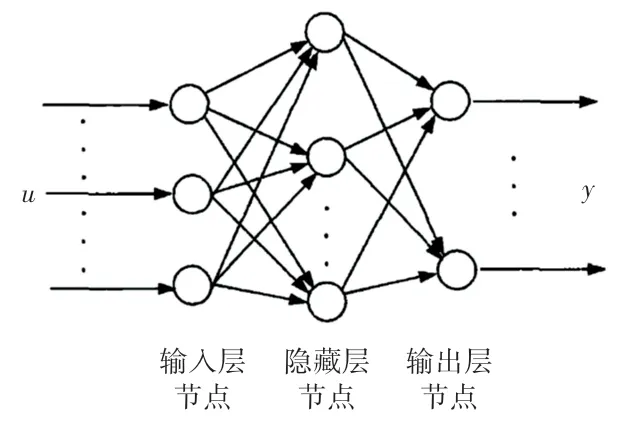
图1 BP 神经网络结构图Fig. 1 Structure of BP neural network

假设输入层节点数为n，隐藏层节点数为l，输出层节点数为m，输入层到隐藏层的权重为ωij，隐藏层到输出层的权重为ωjk， 输入层到隐藏层的阈值为aj，隐藏层到输出层的阈值为bk， 学习速率为η，激励函数为g（x）。 其中，激励函数为g（x） 取sigmoid 函数。 形式如式（1）所示：

隐藏层的输出如式（2）所示：

输出层的输出如式（3）所示：

网络误差如式（4）所示：

其中，Yk为期望输出。

输入层到隐藏层权值的更新公式如式（5）所示：

隐藏层到输出层权值的更新公式如式（6）所示：

隐藏层节点阈值的更新公式如式（7）所示：

输出层节点阈值的更新公式如式（8）所示：

由于BP 神经网络的初始连接权值和阈值是随机选定，可能会使网络陷入局部极值，权值收敛到局部最小值，从而出现网络训练失败，模型的预测精度不高的结果。 因此，本文采用遗传算法对BP 神经网络进行优化，得到权值和阈值的最优解，使模型能够更高效的训练和更精准的预测。

1.2 遗传算法

（1）初始化种群。 种群中的个体由BP 神经网络中输入层到隐藏层的权值、隐藏层的阈值、隐藏层到输出层的权值和输出层的阈值编码而成。

（2）适应度函数。 适应度函数用于表明BP 神经网络中权值和阈值的优劣性，个体适应度值为训练数据预测误差绝对值之和。 适应度函数的计算公式如式（9）所示：

式中：k为系数，n为神经网络输出节点数量，yi为神经网络第i个节点的期望输出，oi为神经网络第i个节点的预测输出。

（3）选择操作。 选择操作从旧群体中以一定概率选择优良个体组成新的种群，以繁殖得到下一代个体，本文采用轮盘赌法，每个个体i被选择的概率pi如式（10）所示：

式中：N为种群规模，Fi为第i个个体适应度值。

（4）交叉操作。 交叉操作是指从种群中随机选择两个个体，通过两个染色体的交换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体，由于个体采用实数编码，所以交叉操作采用实数交叉法［7］。 第j个个体Sj和k个个体Sk在i位的交叉过程如式（11）所示：

式中b为［0，1］区间内的随机数。

（5）变异操作。 为了防止遗传算法在优化过程中陷入局部最优解，在搜索过程中，需要对个体进行变异。 经过交叉操作后得到新的染色体后，随机选择染色体上的若干个基因，将这若干个基因的值进行随机修改，从而更新了染色体的基因，突破了搜索的限制，更有利于获取全局最优解［8］。 选择第i个个体的第j个基因aij进行变异，操作过程如式（12）、式（13）所示：

式中：amax、amin分别是个体i的最大值和最小值，s是迭代次数，Gmax是最大进化次数，r为［0，1］区间内的随机数。

1.3 GA-BP 神经网络预测模型

GA-BP 神经网络预测模型由遗传算法（Genetic Algorithms，GA）优化部分和BP 神经网络两部分组成。 由于种群中的每个个体都包含了BP 神经网络的初始权值和阈值，遗传算法部分的作用是优化BP神经网络的权值和阈值。 通过计算BP 神经网络的误差，得到个体适应度值。 经过遗传算法的选择、交叉和变异操作找到最优适应度值的个体。 对最优个体进行解码，得到权值和阈值，赋值给BP 神经网络，再使用反向传播进行训练。

GA-BP 神经网络预测模型的执行过程如图2所示。

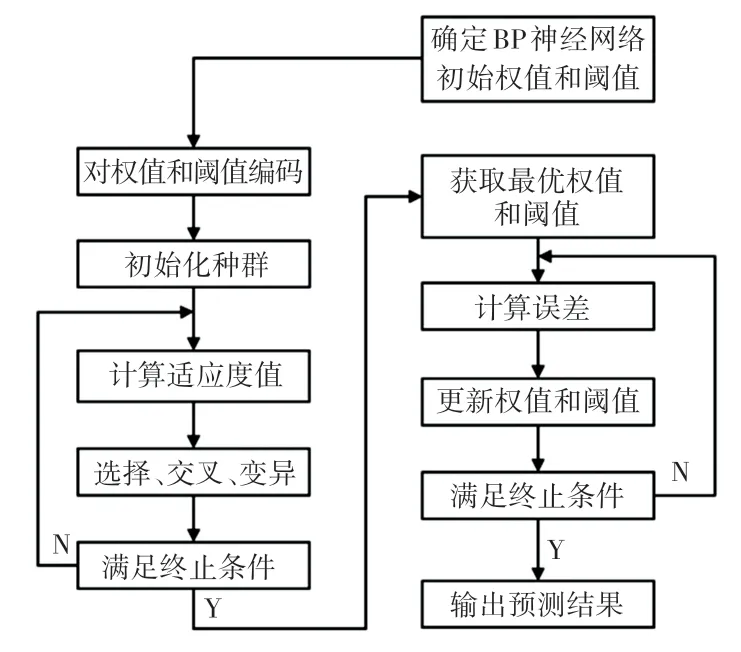
图2 遗传算法优化BP 神经网络流程图Fig. 2 Flow chart of genetic algorithm to optimize BP neural network

2 实验与结果分析

2.1 样本数据采集

本文实验数据采集自连云港赣榆葡萄园第6 号温室，选用温度、湿度、二氧化碳浓度、土壤氮含量、土壤磷含量和土壤钾含量作为样本数据。 每15 min采集一次数据，共采集了2 292 组样本数据。 为了实验测试更方便，本文选用其中2 000 组数据，并将前80%的样本数据作为训练样本，剩余的20%样本数据作为测试样本。 部分样本数据见表1。

表1 部分样本数据Tab. 1 Partial sample data

2.2 模型参数设定

2.2.1 BP 神经网络结构

根据所获得的样本数据，将输入层节点设定为5，即5 个特征，分别为湿度、二氧化碳浓度、土壤氮含量、土壤磷含量和土壤钾含量数据；输出层节点为1 个，特征为温度数据；通过试凑法确定隐藏层节点为7 个。 因此，BP 神经网络的结构为5-7-1。

2.2.2 遗传算法参数设定

由于过多的迭代次数会影响模型的训练效率，且适应度曲线在迭代50 次后的变化幅度不大，因此本实验将进化迭代次数设定为50 次，种群规模为30，交叉概率为0.3，变异概率为0.1。 图3 为遗传算法的适应度曲线。

图3 遗传算法适应度曲线Fig. 3 Genetic algorithm fitness curve

2.3 模型评价标准

为了评定预测模型的性能，本文以平均绝对误差（MAE）、均方误差（MSE） 和平均绝对百分比误差（MAPE） 作为评判预测模型性能优劣的标准。 各评估误差指标的计算公式如式（14）～式（16） 所示：

式中：为模型的预测值，yi为真实值，n为样本数。 所得的值越小，则模型的性能越优异。

2.4 预测结果及分析

通过MATLAB 软件对GA-BP 神经网络预测模型和传统BP 神经网络预测模型进行验证，得到的预测对比结果如图4 所示。

由图4 可知，GA-BP 神经网络预测模型与传统BP 神经网络预测模型相比，GA-BP 的预测效果更优，预测结果更贴近实际值。

评价结果见表2。 可以看出，GA-BP 预测模型的各项误差指标均小于传统BP 预测模型。 实验证明，GA-BP 神经网络预测模型具有更好的预测效果。

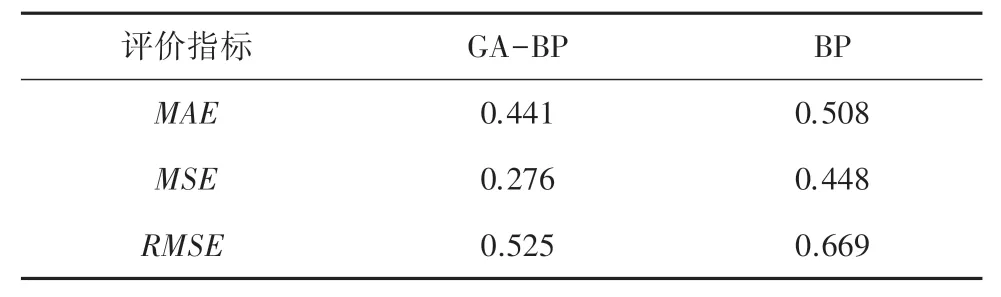
表2 模型的评价指标对比Tab. 2 Comparison of evaluation indicators of the models

3 结束语

本文以温室内湿度、二氧化碳浓度和土壤氮磷钾含量与温度有关的影响因子作为输入量，以温度作为输出量，通过遗传算法优化BP 神经网络的权值和阈值，构建了GA-BP 神经网络预测模型。 实验证明，GA-BP 神经网络预测模型能够更精准的进行温室内温度预测，对于温室管理有一定的参考价值。